二三混水平设计可卷型L2-偏差的新下界*

王治清，罗 彪，欧祖军

(吉首大学数学与统计学院,湖南 吉首 416000)

试验设计被广泛运用到军事、医疗、化工等领域.当各因素与响应的关系未知时,均匀设计是一种非常有效的试验设计方法.均匀设计要求所有设计点都能均匀地分散在整个试验区域内,其均匀性采用偏差来衡量[1].基于不同的角度,学者提出了各种偏差,如中心化L2-偏差[2]、可卷型L2-偏差[3]、Lee偏差[4]、离散偏差[5]、混合偏差[6]等,其中可卷型L2-偏差具有优良的性质,如对称不变性和平移不变性等,因此在衡量设计的均匀性时,可卷型L2-偏差是最常用的偏差.

近几年,可卷型L2-偏差的下界问题受到广泛关注.对于对称因子设计,Fang等[7]首次给出了二水平或三水平设计的可卷型L2-偏差的下界,随后学者们获得了二水平或三水平设计的可卷型L2-偏差的更紧的下界[8-10].对于非对称因子设计,Chatterjee等[11]给出了二三混水平设计的可卷型L2-偏差的下界,随后Zhou等[12]获得了更一般的混水平设计可卷型L2-偏差的下界,Zhang等[13]给出了二三混水平设计的可卷型L2-偏差的更紧的下界,雷轶菊[14]基于可卷型L2-偏差讨论了二四混水平设计的均匀性.笔者主要探讨二三混水平设计的可卷型L2-偏差的新的下界.

1 基本概念

(1)

其中对于i=1,…,n,

引理1[13]对于任意设计d∈U(n;2m13m2),m=m1+m2,有

其中

p1,q1和p2,q2分别为以下方程组的解：

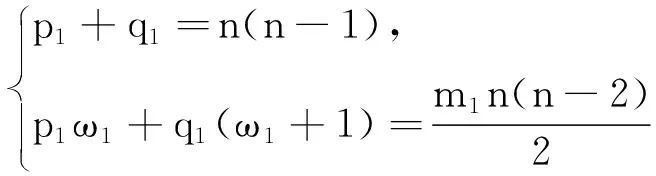
当m1或m2=0时,可得以下结论：

引理2[13]对于任意设计d∈U(n;2m13m2)：

(1)当m2=0时,

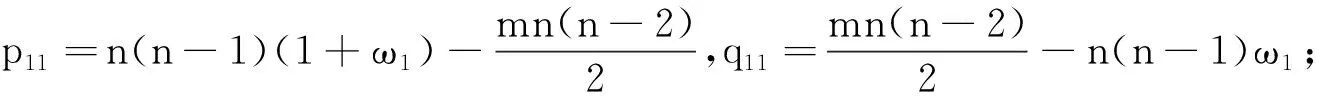
(2)当m1=0时,

2 主要结果

对于任意设计d∈U(n;2m13m2),定义σij={k:uik=ujk,k=1,…,m1},γij={k:uik=ujk,k=m1+1,…,m}.

引理3[13]对于任意设计d∈U(n;2m13m2),有

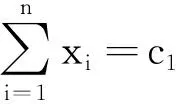
其中p,q为非负实数,且满足p+q=n和pz(k)+qz(k+1)=c.

根据设计d的任意2行之间的重合数,即设计d中任意2行对应位置取相同值的个数，将(1)式改写为包含参数σij,γij的形式，可得如下结论:

定理1对于任意设计d∈U(n;2m13m2),有

证明

由定理1和引理4可以得到任意设计d∈U(n;2m13m2)的可卷型L2-偏差的新下界：

定理2对于任意设计d∈U(n;2m13m2),

有

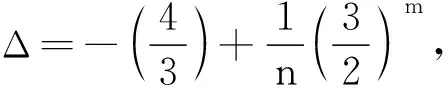
特别地,对于任意设计d∈U(n;2m13m2),当m1或m2=0时,可得如下结论：

推论1对于任意设计d∈U(n;2m13m2):

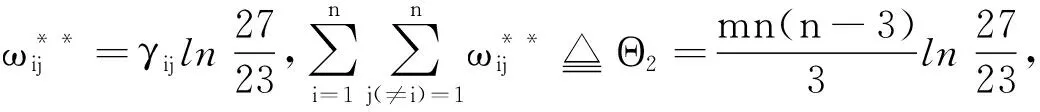
由引理1和定理2可以得到任意设计d∈U(n;2m13m2)的可卷型L2-偏差改进后的新下界:

定理3对于任意设计d∈U(n;2m13m2),有WD(d)≥LBW,其中LBW=max{LB1,LB2}.

当m1或m2=0时,由引理2和推论1可以分别得到任意两水平设计d∈U(n;2m)和三水平设计d∈U(n;3m)的可卷型L2-偏差改进后的新下界:

推论2对于任意设计d∈U(n;2m),有WD(d)≥LBW1,其中LBW1=max{LB11,LB21};对于任意设计d∈U(n;3m),有WD(d)≥LBW2,其中LBW2=max{LB12,LB22}.

3 数值实例

定义设计d的效率为Eff(d)=LBW/WD(d).当设计Eff(d)=1时,设计d为可卷型L2-偏差下的均匀设计;当Eff(d)≈1时,设计d为可卷型L2-偏差下的近似均匀设计.

例1考虑4个设计d1∈U(12;2336),d2∈U(12;21035),d3∈U(12;21135),d4∈U(12;21235).d1来源于文献[13]的表1,d2,d3,d4来源于文献[13]的表2.4个设计的可卷型L2-偏差的平方值、下界和效率见表1.从表1可知,LB2比LB1更紧,且d1,d4是均匀设计,d2,d3是近似均匀设计.

表1 设计d1,d2,d3,d4的可卷型L2-偏差的平方值、下界和效率Table 1 Values of Squared Wrap-Around L2-Discrepancy,Lower Bound and Efficiency for Designs of d1,d2,d3,d4

例2考虑如表2所示的设计d5∈U(12;21135),n=12,m1=11,m2=5,于是WD(d5)=68.828 0,LB1=67.856 5,LB2=67.932 9,因此Eff(d5)=0.987 0,由此可知d5是近似均匀设计,且LB2比LB1更紧.

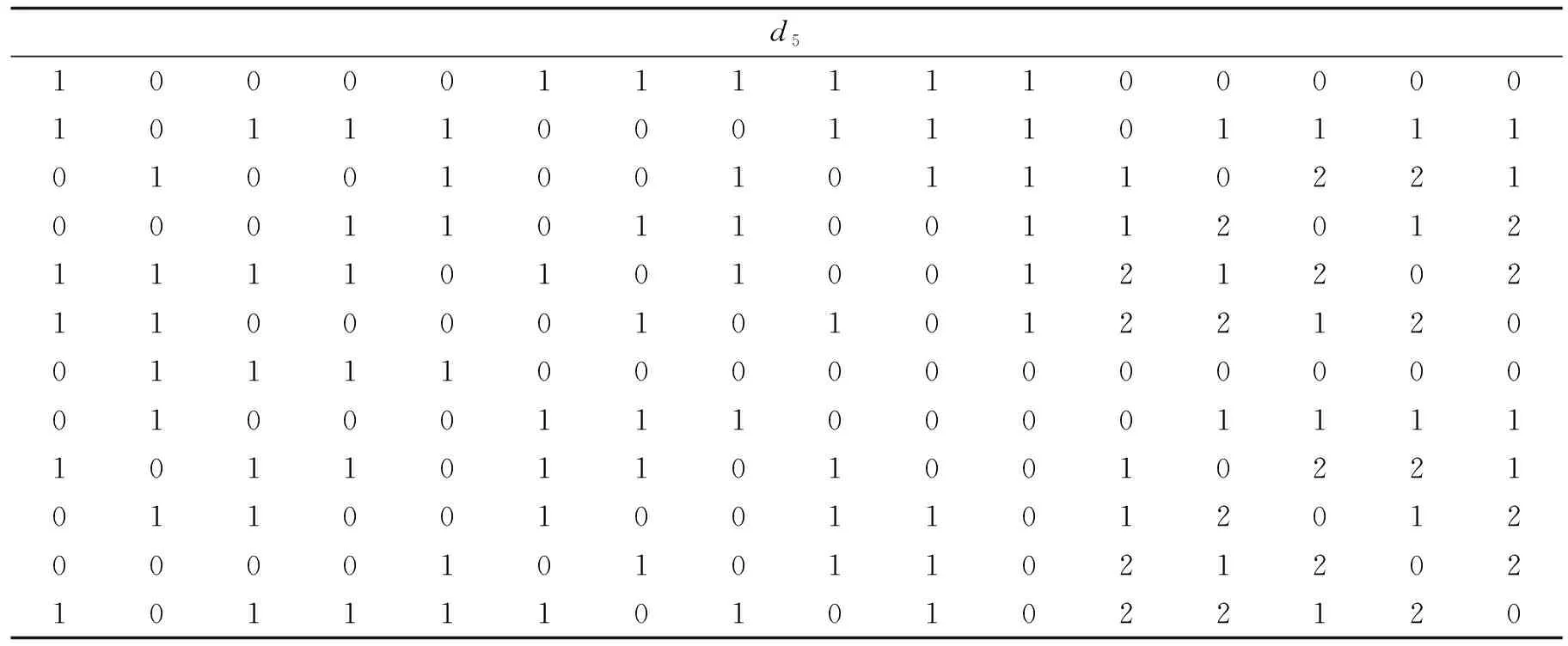
表2 设计d5Table 2 Design of d5

4 结语

基于可卷型L2-偏差的均匀性准则讨论了二三混水平因子设计的均匀性,获得了其可卷型L2-偏差的新下界.数值实例表明,新下界是紧的,且与文献[13]的结果相比,新下界更精确,因此新下界可作为衡量和搜索均匀设计的基准.此外,本研究关于二三混水平设计均匀性的讨论可为高水平设计和更一般的混水平设计的均匀性研究提供参考.