三阶半线性中立型微分方程的振动性*
2021-12-16贾对红
贾对红
(长治学院数学系,山西 长治 046000)
近年来,许多学者对三阶微分方程的振动性进行了研究,取得了许多成果[1-6].笔者拟在文献[7]的基础上,利用Riccati变换和Philos型积分技巧研究一类三阶半线性中立型分布时滞微分方程

(1)

1 预备知识
函数x(t)称为方程(1)的一个解,如果函数z(t)和r(t)|z″(t)|α-1z″(t)连续可微,且在[t0,+∞)上x(t)满足方程(1).方程(1)的一个非平凡解称为振动的,如果它有任意大的零点;否则,称它为非振动的.若方程(1)的一切解都是振动的,则称方程(1)是振动的.
假设下列条件成立:

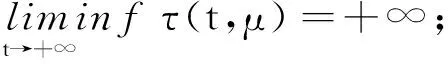



引理1[8]若x(t)是方程(1)的最终正解,则存在t1>t0,当t>t1时,有:
(ⅰ)z(t)>0,z′(t)<0,z″(t)>0;
(ⅱ)z(t)>0,z′(t)>0,z″(t)>0.
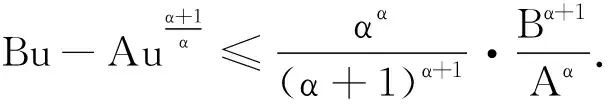
引理3设x(t)是方程(1)的最终正解,且z(t)满足引理1(ⅰ),若
(2)


(3)

(4)


于是
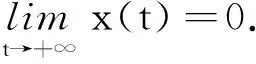
2 主要结果及其证明
设D={(t,s):t0≤s≤t<+∞},D0={(t,s):t0≤s (1)H(t,s)>0,(t,s)∈D0,H(t,t)=0,t≥t0; 定理1假设(H1)~(H6)和(2)式成立,且存在ρ∈C1([t0,+∞),R+)和∀(t,s)∈D0,满足 (5) 其中 则方程(1)的解x(t)或者是振动的,或者当t→+∞时趋向于0. 证明设方程(1)有非振动解,则x(t)为最终正解或最终负解.不妨设x(t)为最终正解(最终负解的证明类似),且x(τ(t,μ))>0,x(g(t,ξ))>0,t≥t1≥t0. 若z(t)满足引理1(ⅱ),即z(t)>0,z′(t)>0,z″(t)>0,z(t)是单调递增函数,则有 (6) 由(H5),(H6)和(6)式,可得 可以看出,r(t)(z″(t))α是单调递减函数,且t>s时,r(t)(z″(t))α (7) (8) (8)式两边同时对s从t0到t积分,可得 (9) 因此对于∀t≥s≥t1,由(8),(9)式有 (10) 令 (11) 由引理2可得 (12) (13) 对(13)式两边同时从t1到t积分,可得 当t→+∞时,由(5)式可知w(t)→-∞,这与w(t)>0矛盾.证毕. 定理2若存在函数ρ∈C1([t0,+∞),R+)使得(2)式成立,且满足 (14) 则方程(1)的解x(t)或者是振动的,或者当t趋于+∞时趋向于0. 证明设方程(1)有非振动解,则x(t)为最终正解或最终负解.不妨设x(t)为最终正解(最终负解的证明类似)且x(τ(t,μ))>0,x(g(t,ξ))>0,t≥t1≥t0. 若z(t)满足引理1(ⅱ),则令 (15) 对(15)式从t0到t积分,可得 当t→+∞时,由(14)式可知u(t)→-∞,这与u(t)>0矛盾.证毕. 定理3假设(H1)~(H6)和(2)式成立,若存在ρ∈C1([t0,+∞),R+)和∀(t,s)∈D0,满足 (16) 则方程(1)的解或者是振动的,或者当t趋于正无穷时趋向于0. 证明设方程(1)有非振动解,则x(t)为最终正解或最终负解.不妨设x(t)为最终正解(最终负解的证明类似)且x(τ(t,μ))>0,x(g(t,ξ))>0,t≥t1≥t0. 若z(t)满足引理1(ⅱ),则由定理1的证明可知(11)式成立,即 (17) (18) 整理得到 即 (19) 于是 (20) 联立(19),(20)式,可得 对于∀t≥t1>t0,有 这与(16)式矛盾.证毕. 定理4假设(H1)~(H6)和(2)式成立,ρ∈C1([t0,+∞),R+),φ∈C([t0,+∞),R),H∈X,对于∀T≥t0,有 (21) (22) (23) φ+(s)=max{φ(s),0}, 则方程(1)的解或者是振动的,或者当t趋于正无穷时趋于0. 证明若z(t)满足引理1(ⅰ),则由引理3即证. 若z(t)满足引理1(ⅱ),则由(22)式可知对于∀t1>t0,有 即对于∀t1>t0,有 φ(t1)≤w(t1). (24) 由(19)式可得 (25) 由(21)式可知,存在ε>0,使得 (26) 由N的任意性,有 这与(25)式矛盾,因此 由(24)式可得 这与(23)式矛盾.证毕. 考虑方程 该方程的解或振动或趋于0.
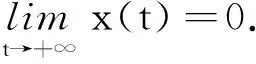


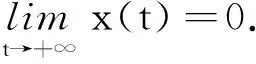
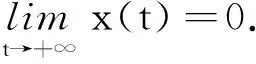
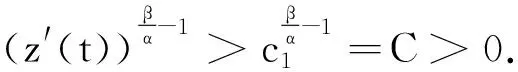


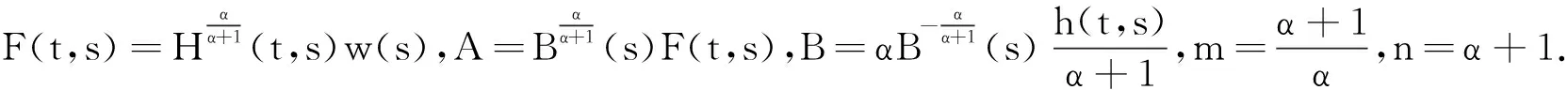
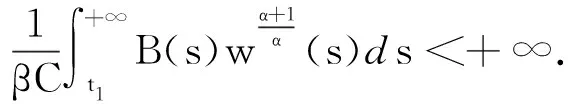


3 应用举例
