基于全局稀疏梯度与低秩张量正则化的多源多波段图像融合方法∗
2021-12-15黄志忠潘
黄志忠潘 汉
(1.桂林航天工业学院电子信息与自动化学院,广西 桂林541004;2.上海交通大学航空航天学院,上海200240)
随着星载传感器技术的发展,高光谱、多光谱、可见光和红外等传感器得到了广泛应用。然而,高光谱具有较高的光谱分辨率但是空间分辨率较低。多光谱图像具较高的空间分辨率,然而光谱分辨率相对较低。全色图像具有比较高的图像空间分辨率。多模图像融合通过集成多模敏感器的细节信息,可以综合成高质量的图像,提高图像信息的利用率,可为后续的目标检测与识别提供技术支撑[1-2]。
国内外针对图像融合问题已经提出许多算法[3-5]。相对于融合类型来说,目前主要有高光谱与多光谱图像融合、高光谱与全色图像融合,以及多时相图像融合等。然而,常用的图像融合方法只能融合两个模态传感器的信息。与此同时,如果设计一个具有较好融合性能的正则化方法仍是一个比较重要问题。
目前,一种比较好的正则化方法是变分正则化方法[6]。该方法的成功之处在于可以保留图像中的边缘信息,但是会对图像纹理过平滑,也就是阶梯效应。虽然,文献[3]提出了一种基于黎曼流形优化的多源多波段图像融合方法。但是,多模图像空间信息与频谱信息的高阶相关性及其内在结构特性还没有得到充分的利用。
针对上述问题,本文基于图像域的非局部自相似框架,引入复合正则化方法,提出了基于全局稀疏梯度与低秩张量正则化的多模图像融合方法,并应用于多源多波段图像融合,也就是高
光谱、多光谱与全色图像的融合。
本文的主要工作归纳如下①研究了一种基于全局稀疏梯度与低秩张量正则化的多源多波段图像融合模型,并给出相应的优化求解方法;其中,多源多波段图像的频谱信息使用全局稀疏梯度正则化方法,空间信息使用低秩张量正则化方法。②应用于多源多波段图像融合,实现高光谱、多光谱与全色图像的融合。仿真实验验证了该方法的可行性和有效性。
本文的主要结构如下:第1节给出了多源多波段图像观测模型,然后推导了基于全局稀疏梯度与低秩张量正则化的多源多波段图像融合模型。第2节给出求解该模型的交替方向乘子法。第3节对所提方法进行验证,并给出与其他方法的对比结果。
1 多源多波段图像融合问题建模
1.1 多源多波段图像观测模型
本文使用文献[3]中的观测模型。本文使用Z∈RL×N表示高光谱图像,L用于表示光谱波段数,N用于图像相应的像素个数。

式中:Rk是光学传感器产生的谱响应,其对应的观测值是Om;Bm∈RN×N是与波段相对应的点扩散函数,也就是空间模糊矩阵。Sm是一个满足STmSm=IN的稀疏矩阵。Pm是加性扰动矩阵,代表着与成像传感器相关的噪声。
1.2 基于全局稀疏梯度与低秩张量正则化的多源多波段图像融合模型
本小节引入复合正则化方法,考虑多模图像的全局稀疏梯度正则化方法,以及低秩张量正则化方法,给出基于全局稀疏梯度与低秩张量正则化的多源多波段图像融合模型。本文使用线性混合模型[7](Linear mixture model)表征观测场景中的成像数据。给定的端元数目记为Q,且满足Q≪L,将Q个端元构建为E∈RL×Q的列,那么可将Z分解为:

式中:A∈RQ×N是端元丰度矩阵,P是相应的加性扰动矩阵。
将式(2)代入(1),我们可以得到:
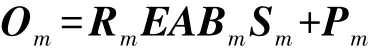
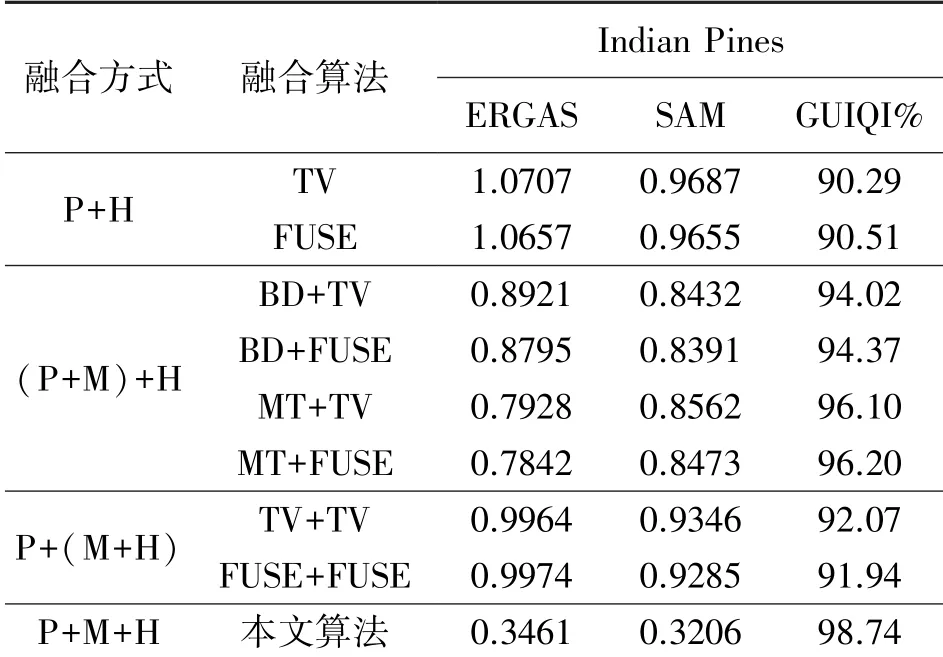
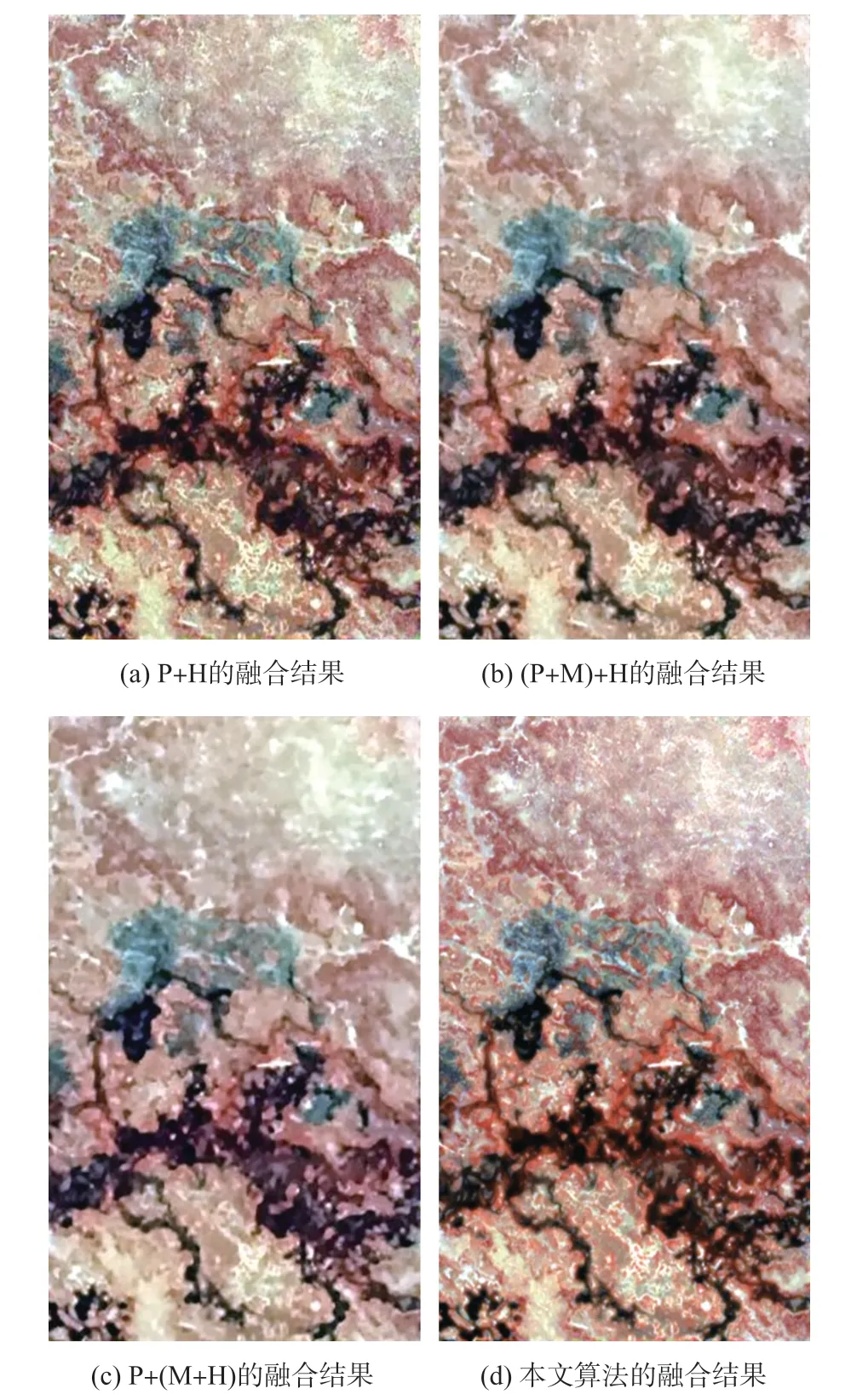
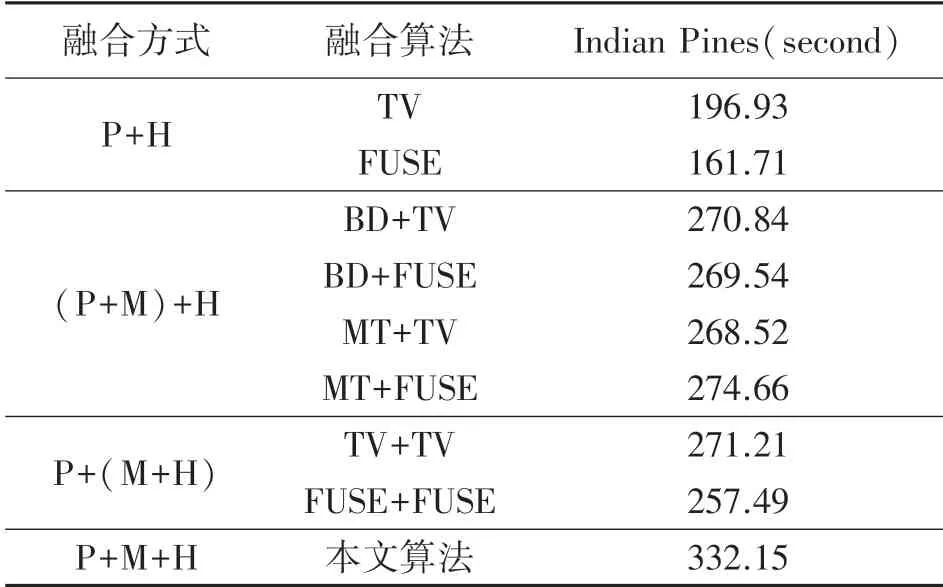
为实现任意空间分辨率和光谱分辨率情况下的多源多波段图像的融合,本文使用下面的多种正则化方法:①对A施加非负及系数和为1的约束,也就是A≥0且1TQA=1TN;②对A使用全局稀疏梯度正则化方法,也就是‖∇cA‖p;其中,∇c代表着沿着光谱方向的全局稀疏梯度正则化方法;此外,0 最后,本文给出基于全局稀疏梯度与低秩张量正则化的多源多波段图像融合模型: 式中:α>0和β>0分别是相应正则化项的非负正则化参数。 本文使用交替方向乘子法(Alternating direction method of multipliers,ADMM)求解问题(3)。其中主要思想是变量分离策略,也就是引入辅助变量Um∈RQ×N(m=1,2,…,M)、V、W,以及K。在此基础上,考虑A具有非负且系数和为1的约束,引入下面的示性函数: 本文提出的算法流程,如表1所示。 表1 基于全局稀疏梯度与低秩张量正则化的多源多波段图像融合算法流程 为了验证本文算法的有效性,我们考虑全色图像、多光谱图像和高光谱图像,通过数值仿真的方式评估融合性能。本文的仿真实验使用二个遥感数据集:Botswana(400×240×145)、Washington DC Mall(400×300×191),以及Indian Pines(400×400×200)。其中,400×240×145代表着遥感数据集的空间分辨率是400×240,波段数是145。本文的所有仿真实验及算法运行环境是基于Intel CPU i7-9750H 2.6 GHz和8 GB内存的笔记本电脑。所有的算法使用MATLAB语言编程。 基于上述的遥感数据,为了生成高光谱图像,本文对所输入的图像二维高斯模糊核(13×13,方差=2.12)进行卷积操作,然后对所产生的图像以4的比率进行下采样。为了生成多光谱图像,本文首先将二维高斯模糊核(7×7,方差=1.06)应用于输入的图像数据集,以2的比率进行下采样,最后使用Landsat 8多光谱传感器的光谱响应特性进行图像降质。另外,本文对所生成的图像加入高斯噪声,并使得所产生的多光谱和高光谱图像的信噪比分别是30 dB。与此同时,全色图像的信噪比设置为40 dB。 已有的多波段图像融合算法仅能实现对两个传感器的图像融合,例如多光谱图像与高光谱图像融合、全色图像与多光谱图像融合等。为了进行对比分析,本文使用相关的融合算法实验三个传感器图像的融合。首先,本文使用二种多光谱图像与全色图像融合算法:①基于局部参数估计的波段相关空间细节算法[11](Band-dependent spatial detail,BD);②基于高通调制的调制传输函数广义拉普拉斯金字塔算法[12](Modulation-transfer-function generalized Laplacian pyramid,MT)。 本文使用两种算法进行多光谱图像与高光谱图像的融合:①基于全变分正则化及子空间的融合方法[6](Total variation,TV);②基于Sylvester方程的快速融合方法[13](Fast fusion based Sylvester equation,FUSE)。 为了评估算法的融合性能,本文使用常用的三种评估指标:①相对无量纲全局误差指标[14](ERGAS);②波谱角[15](spectral angle mapper,SAM);③广义通用图像质量指标[16](Generalization of the universal image quality index,GUIQI)。其中,ERGAS和SAM的值越小,代表着融合性能越好。与此同时,GUIQI的值越大越好。 表2~表4分别给出了多个算法在高光谱数据集Botswana、Washington DC Mall与Indian Pines的融合性能评估结果。其中,较好的融合结果使用粗体表示。此外,P+H用于表示全色图像与高光谱图像的融合方式。(P+M)+H代表着先进行多光谱图像与全色图像的融合,然后再与高光谱融合的方式。P+(M+H)代表着先进行多光谱图像与高光谱图像的融合,然后再与全色图像融合。P+M+H表示同时进行多光谱图像、高光谱图像、全色图像的融合方式。 观察表2~表4中的融合性能评估结果,我们可以发现本文所提出的算法具有较好的融合性能。通过对比,我们可以发现不同的融合算法具有不同的多源多波段图像融合与图像细节的建模及挖掘能力。最后,基于融合性能指标ERGAS、SAM和GUIQI的定义,本文所提出的算法可以融合较多的局部细节信息。 表2 基于Botswana数据集的多源多波段图像融合性能定量分析结果 表3 基于Washington DC Mall数据集的多源多波段图像融合性能定量分析结果 表4 基于Indian Pines数据集的多源多波段图像融合性能定量分析结果 为了在视觉上进行融合质量评估,本文给出了Botswana与Indian Pines数据集的多源多波段图像融合结果(Washington DC Mall数据集与Botswana数据集的处理视觉效果基本相同),如图1和图2所示。其中,高光谱图像的信噪比是30 dB;多光谱图像的信噪比是30 dB;全色图像的信噪比是40 dB。其中,P+H代表着全色图像与高光谱图像的融合;(P+M)+H代表着先融合全色图像与多光谱图像,然后再与高光谱进行融合;P+(M+H)代表着先融合多光谱与高光谱图像,然后与全色图像进行融合。 图1(d)和图2(d)给出了本文提出算法的融合结果。其中,图1(d)所显示的融合结果包含有波段(32 26 6);图2(d)所显示的融合结果包含有波段(30 22 3)。从中我们可以看到,本文提出的算法具有较好的融合效果,细节信息比较多。这些视觉上的融合效果验证了本文提出的算法的有效性。 图1 基于Botswana数据集的多源多波段图像融合视觉结果对比分析 图2 基于Indian Pines数据集的多源多波段图像融合视觉结果对比分析 为了对不同融合算法的时间复杂度进行定量分析,本文在同等条件下,通过测量算法运行时间的方式,进行性能评估,对基于Indian Pines数据集的处理比较(对Botswana和Washington DC Mall数据集处理具有相同比例的效果,因为算法相同只是数据不同而已)如表5所示。其中,运行时间较少的算法是FUSE算法。但是,结合之前的性能评估结果,我们可以看到所提出的算法只增加了一些计算时间,但是具有较好的融合性能。 表5 基于Indian Pines数据集的算法运行时间对比单位:s 本文针对多源多波段图像融合问题,引入复合正则化方法,提出了一种基于全局稀疏梯度与低秩张量正则化的多源多波段图像融合模型。该正则化方法包含有全局稀疏梯度正则项与低秩张量正则项。本文采用基于ADMM优化框架求解融合模型。本文所提出的方法可以实现了三种视觉传感器图像的同时融合。仿真实验及融合性能评估结果验证了本文所提出算法的有效性。本文的理论与技术成果为基于多传感器融合的目标检测与识别提供理论与技术基础。
2 基于全局稀疏梯度与低秩张量正则化的多源多波段图像融合
2.1 交替最小化框架

2.2 求解子问题

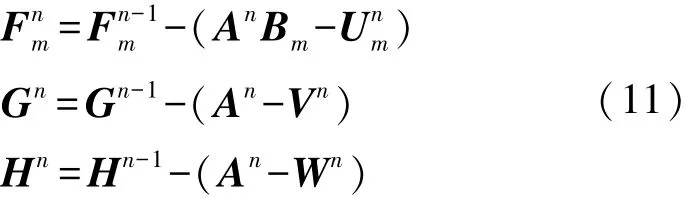

3 实验结果与讨论
3.1 数据集及仿真实验参数
3.2 实验结果



4 结论
