耦合高速列车风下的输电线路跨越封网风偏响应研究

2021-12-15黄士君王城禹江力强曹枚根

浙江电力 2021年11期

黄士君，何畅，黄涛，王城禹，江力强，曹枚根

（1.国网江苏省电力有限公司建设分公司，南京 210000；2.中南大学土木工程学院，长沙 410075；3.北方工业大学，北京 100144）

0 引言

在我国2035 年远景交通规划中，计划建成高速铁路7 万km，形成6 主轴、7 走廊和8 通道的国家综合立体交通网络[1]。而随着以“特高压”为代表之一的“新基建”的提出，输电线路工程建设方兴未艾。

作为线路工程，输电线路与运营中的高速铁路的交叉跨越日益频繁。输电线路的架设不应影响高速铁路的正常运营。另外，考虑高速铁路接触网的高压特性，常在架设输电线路与高速铁路接触网之间设置绝缘封网[2]。2011 年，孙伟军等人提出利用全封闭绝缘封网完成了浙江省首例500 kV 输电线路跨越高速列车施工[3]。2018 年，袁团林提出了利用悬索架空网构架作为输电线路跨越高速列车施工的封网结构[4]。张富平等人提出了组合矩阵式跨越架的安装技术[5]。采用防护横梁架设封网的方法也逐渐应用于跨越工程中[6]。张潇、张建等人研究了特高压输电线路利用封网跨越高速铁路的施工方法[7-8]。南方电网的滇西北工程中，悬索斜封网跨越高速铁路的施工方案也得以采用[9]。

列车在高速运行时，与周围空气相互作用，将产生沿列车前进方向、垂直于行车水平方向及竖直方向的三向风压。关于列车风国内外学者已开展了十分广泛的研究。Gallagher 和Bell 等人分别采用眼镜蛇探针测试了移动列车和静止列车模型周围的列车风，测试结果取得了较好的一致性[10-11]。牛继强、田红旗和刘润东等人重点研究了高速列车会车过程中由列车风引起的压力波对列车和周围防风措施带来的影响[12-14]。周小刚等人研究了钢箱梁斜拉桥上列车风及其风致振动响应[15]。总体上目前大家对列车风的认识已经十分全面，但自然风和列车风耦合效应对柔性结构风致振动响应影响的研究相对缺乏。

由于悬索结构的刚度较小，其易在外力作用下产生较大的变形[16]。高速铁路除对与其交叉的输电电磁场有影响外[17]，2019 年，张玉婵、何正浩研究了交叉跨越输电线路高速列车流场分布，预测列车风引起的输电线路振动将加剧输电线路的疲劳损伤[18]。2020 年，高峰等人探究了由高速列车穿越风引起的输电线路振颤，其研究结果表明高速列车风引起的振动频率与线路自振频率接近，易引发共振[19]。

封网结构的受风面积大、距离列车近、刚度柔、阻尼小，在列车风和自然风荷载耦合作用下，其风致振动响应明显。封网风偏可能侵入高速列车限界，封网的上下风致振动也可能造成上部施工的安全事故。然而，目前缺乏针对封网结构风致振动响应分析的规范和指南。因此开展自然风和列车风耦合作用下的输电线路跨越封网结构响应研究具有重要意义。以往主要研究高速列车风及其引起的结构响应，但在实际工程中，高速列车风通常和自然风耦合出现。自输电线路跨越封网位置处，自然风风速一般大于高速列车风风速，不应忽略。另外，高速列车外形将改变自然风干扰源，其产生的紊流可能放大封网结构的风偏响应，影响高速列车运营及输电线路施工安全。为研究高速列车风与自然风耦合作用下输电线路跨越封网的风偏响应，本文以CRH380A 型列车为研究对象，计算了列车运行时的高速列车风与自然风耦合风速剖面。建立了常见施工封网的数值模型，研究了其在耦合风荷载作用下的动力响应。另外，对工程中常见参数范围内的封网结构开展了参数分析，揭示了耦合风荷载对其风偏的影响规律。

1 耦合高速列车风

在自然风风速大于25 m/s 时，高速列车将停止运行，故本文采用25 m/s 的自然风速与350 km/h 运行速度高速的列车耦合，分析其产生的耦合列车风。

1.1 耦合高速列车风计算模型

本次数值计算采用现役CRH380A 动车组，列车模型为“头车+中车+尾车”的三列编组形式[10-11]，模型总长L 为78 m、高H 为3.7 m、宽B 为3.38 m。另外，本次模拟忽略其受电弓、车轮、门窗和转向架等部件，并对车厢连接处进行了简化，简化后的列车计算模型如图1 所示。

图1 CRH380A 型高速列车数值模型

为避免计算域边界对列车流场的干扰，列车位于初始位置时，车尾距离计算域入口100 m，车头距计算域中心122 m。在已有研究结果的基础上[12]，本次数值模拟计算域的长、宽和高分别为600 m、150 m 及100 m，如图2 所示。计算域前、后、顶面定义为对称边界。计算域左侧定义为速度入口边界，其风速为25 m/s。计算域右侧定义为压力出口边界，底面和列车定义为无滑移壁面边界。为实现列车移动，本文采用与文献[13]相同的铺层法。在静止区域和列车移动区域建立一层Interface 界面，从而实现列车移动过程中流场信息的交换。

为获得封网附近的风速剖面，从列车车顶上方一倍车高处开始每0.5 m 设置一个风速监测点，共计布置34 个测点，测点高度范围为3.7～20.7 m，如图3 所示。

图3 耦合高速列车风速监测点

本次计算列车运行速度为350 km/h，与25 m/s 横风耦合后，合成速度为100.39 m/s，基于空气流动速度的马赫数仍小于0.3，可视为不可压缩流体。因此，本文采用非定常、黏性、不可压缩N-S 方程和RNG k-ε 湍流模型来模拟高速列车的运行过程[20-21]。RNG k-ε 湍流模型的输运方程类似于标准k-ε 模型，湍流动能k 和耗散率ε 方程为：

式中：μeff表示有效动态粘度，等于分子和湍流粘度之和；Gk为平均速度梯度引起的湍流动能；模型常数C1ε=1.42；ρ 为流体密度；ui为流体流速；xj为计算域中微元的空间坐标；αk为k 有效普朗特数的倒数；YM为可压缩湍流中波动膨胀对总耗散率的贡献；可由式（3）计算得到：

式中：C2ε=1.68；η0=4.38；β=0.012；η=Sk/ε，S 表示应变率张量的范数[22-24]。利用流体计算软件Fluent 进行计算，采用SIMPLEC 方法求解，计算时间步长取0.008 57 s。

1.2 模型网格划分及验证

网格划分采用结构网格与非结构网格相结合的混合网格。采用结构网格划分，最大尺寸为1.5 m，最小尺寸为0.2 m；移动区域列车几何结构复杂，采用非结构网格划分，列车表面网格最大尺寸为0.1 m，具体有限元网格划分如图4 所示。为验证数值模拟结果的网格无关性，分别开展了稀疏网格（2 100 万）、中等网格（3 180 万）和精细网格（4 300 万）3 种网格精度下的试算工作。试算不考虑横风影响，列车运行速度为300 km/h。试算结果如图5 所示，其与文献[14]中以302 km/h运行的CRH3 动模型试验结果对比分析表明：在考虑列车模型差异的情况下，精细网格计算结果与动模型试验结果取得了较好的一致性，因此本次数值模拟计算具有较高的可信度。

图4 CRH380A 型高速列车单元划分

图5 高速列车风计算模型验证

1.3 耦合高速列车风的影响分析

25 m/s 横风（垂直于列车运行方向）下列车以350 km/h 时速穿过计算域时，计算域内不同位置处的各向风速时程如图6 所示。由图6（a）可知，在列车驶过封网位置的过程中，列车前进方向风速出现一对明显的“头波”和“尾波”。“头波”和“尾波”的峰-谷值随风速监测点高度的增大而快速减小。2.00H 高度处，风速峰-谷值约为2.5 m/s。另外，在横向，由于列车的出现，横风风速被显著放大，2.00H 高度处放大因子约为23%，这与规范[25]中风吹过小山在山顶形成的风速放大效应是一致的。同时，此结论也与Li 等人在列车-扁平箱梁系统中观察到列车车肩处的风速加速效应一致[26]。在竖直方向，风速时程出现了另一对“头波”和“尾波”，2.00H 高度处峰-谷值约为5.3 m/s，数值强度略大于图6（a）所示结果，这是由于横风流过列车后在竖直方向形成一个风速分量造成的。

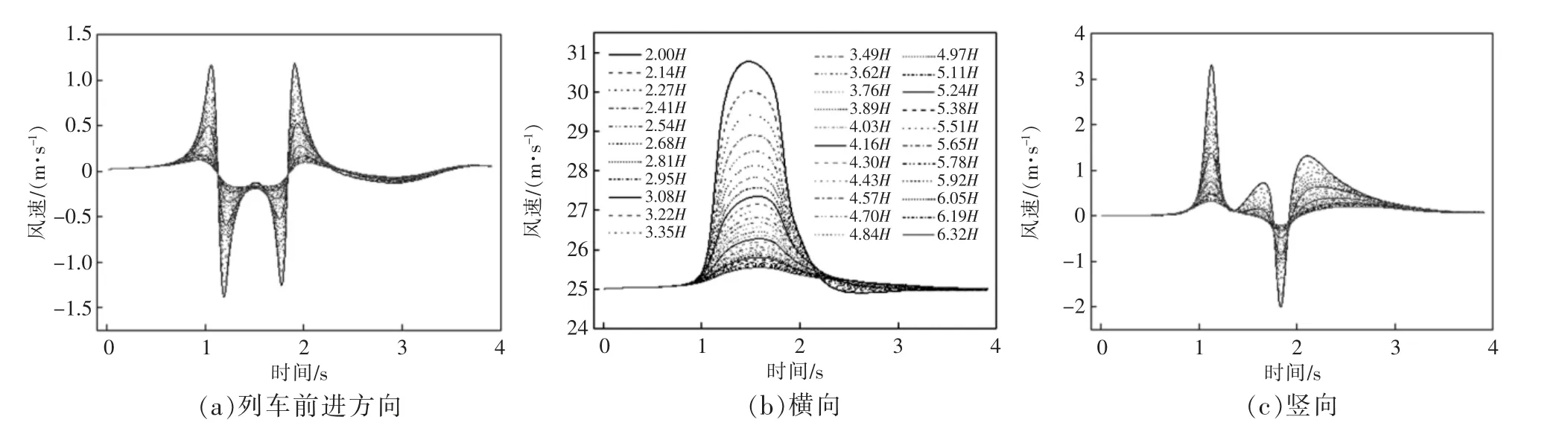
图6 自然风列车风耦合作用下的风速时程

基于上述分析可知，在输电线路放线封网可能架设的高度范围内，横风和列车风耦合作用主要表现为横风放大效应和“头波-尾波”的冲击效应。上述两种效应将对封网的风偏和风致振动响应产生一定的影响。

另外，本文还计算了未考虑自然风时的高速列车风风压。在列车车速为350 km/h 时，列车头部周围风压分布如图7 所示。由图7 可知，在距离列车边缘2B 意外区域，列车行驶对风压的影响较小。

图7 时速350 km/h 时列车头部周围风压分布

2 输电线路跨越封网耦合风致响应

2.1 输电线路跨越封网结构及其数值模型

常见输电线路跨越高速列车施工封网结构示意如图8 所示。输电线路跨越封网主要由承载索、撑杆等主要部件及绝缘网、封网绳、拉网绳、支撑滑车、滑轮等附属部件组成[3]。本文算例中，封网结构共含有四根承力索，索间距8 m。承力索由Φ16 mm 迪尼玛绳组成。封网水平跨度300 m，两端均安装在现场临时拼装的跨越塔架上。在算例中，封网承力索的初始张拉力设为80 kN。封网底部距离列车车顶高度为8 m。封网在其中部跨越高速铁路，在封网中部设置9 根由玻璃钢复合材料构成的撑杆，以维持封网承力索间的距离，并承担输电线路断线等偶然荷载。

图8 封网结构示意[3]

由于封网结构主要由其承力索及撑杆承载，故在数值模型中，忽略了其他附属部件，仅考虑承力索与撑杆的作用。本文在Abaqus 有限元分析软件中模拟封网结构，采用B31 非线性梁单元模拟封网承力索及撑杆。封网结构有限元模型俯视如图9 所示。另外，模型中通过在初始场中定义预应力给封网承力索施加80 kN 预拉力。由于跨越塔架离高速铁路较远，在列车风影响范围外（图7），故在数值模型中未考虑跨越塔架，而将封网封网承力索直接固定在支座上。在该算例中，列车前行方向与封网方向垂直。有限元计算中，通过施加重力场进行封网承力索找形。另外，根据高速列车风速及风压的分布情况，将风荷载简化为集中荷载，施加在承力索的节点上。

图9 封网结构有限元模型（俯视）

2.2 封网数值模型验证

将封网承力索简化为悬索，其重点档距的弧垂计算值f计为[27]：

式中：ω 为迪尼玛绳的单位长度自重力；D 为承力索张力；l 为长度。

目前暂无关于封网风偏响应的试验或现场实测研究。为验证本文有限元模型的准确性，本文共计算了无撑杆时该型封网在承力索张力分别为20 kN、50 kN、80 kN、110 kN、140 kN 时的弧垂。不同张力下，由有限元模型及式（4）计算得承力索弧垂对比如图10 所示。由图10 可知，承力索有限元模型计算结果与理论公式计算接近，该有限元模型及建模方法可用于后续封网结构响应分析。

图10 封网有限元模型验证

2.3 封网耦合风致振动响应

2.3.1 封网承力索内力响应

在自然风与高速列车风耦合作用下，封网承力索端部及中部内力响应如图11 所示。由图11可知，对于同一根承力索，其端部与中部内力响应基本一致。校核封网承力索在风振下的强度时，可仅考虑其端部截面的轴力响应。1 号与4号承力索（图9）仅一侧安装撑杆，故其内力响应与2 号、3 号承力索有较大区别。两侧均安装撑杆的承力索内力响应大于边侧承力索响应。校核承力索强度时，建议考核中部承力索的内力响应。预张力为80 kN 时，封网承力索最大张力为81.33 kN。封网承力索最大张拉力主要由其预张力决定。对于Φ16 mm 迪尼玛绳，其理论破断拉力为215 kN[27]。在25 m/s 自然风与350 km/h 高速列车风耦合作用下，封网承力索强度安全系数为2.6。

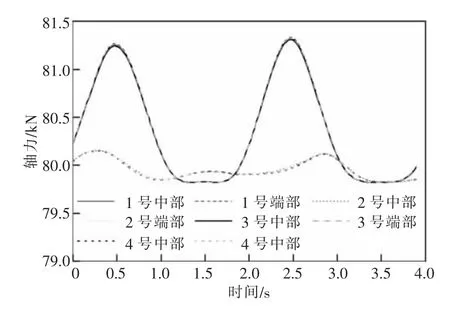
图11 耦合风荷载下承力索轴力时程

2.3.2 封网承力索风偏响应

在耦合高速列车风荷载作用下，封网承力索中部在竖直方向的风致振动位移如图12 所示。由图12 可知，在耦合风荷载作用下，封网将出校较大幅度的上下振荡。在该算例参数下，封网中部承力索（3 号、4 号索）的上下振幅分别为1.46 m 及1.18 m。重力作用下，承力索出现向下弧垂。在风荷载作用下向上振动时，承力索长度缩短，弧垂减小。向下运动时，承力索在风荷载及其惯性作用下长度伸长。承力索具有较强的几何费现象，其向下运动时刚度大于向上运动刚度。在耦合列车风荷载作用下，承力索向下振荡位移小于向上振荡位移。另外，由图12 可知，封网上下振动幅度较大。在风荷载作用下，封网向下振动可能侵入高速铁路限界。封网向上的位移也可能影响上部施工安全。在进行施工封网的架设时，应考虑此振动距离的影响。

图12 耦合风荷载下承力索竖直位移时程

耦合高速列车风荷载作用下，封网承力索横向风偏时程如图13 所示。由图13 可知，承力索整体朝列车行进方向发生风偏。在重力荷载及风荷载作用下，封网撑杆发生弯曲。撑杆的弯曲将牵拉其4 号索背离列车前进方向振动。由于2号、3 号索两侧均安装有玻璃钢撑杆，故其横向风偏小于1 号、4 号索。在评估封网承力索结构的横向风偏时，可校核其边承力索的风偏响应。另外，由图13 可知，该型封网水平向风偏达0.32 m。在进行施工封网结构设计时，需考虑其水平风偏响应，确保其在风荷载下位置稳定性，保证施工安全。

图13 耦合风荷载下承力索横向位移时程

3 封网结构参数分析

为研究不同参数对输电线路跨越施工封网在耦合风荷载下的内力及风偏响应的影响，本节针对封网承力索及撑杆结构开展参数分析。本节考虑了封网与列车行进方向夹角、封网安装高度、封网跨度及封网承力索预张力等参数。

3.1 封网预张力及跨度的影响

对于悬索结构，由于其具有较强的几何非线性，其索内张力对其动力响应有较大影响。另外，考虑施工场地不同的跨越条件，封网跨度不尽相同。本节对封网承力索预张力及封网跨度进行参数分析，探究其对封网承力索轴力其风偏的影响。

不同跨度及预张力下，封网承力索张力如表1 所示。相较预张力，承力索轴力增大值如图14所示。由图14 可知，不同跨度及不同预张力时，封网承力索的轴力变化较小，其主要由预张力确定。定义承力索轴力增量百分比α 为：

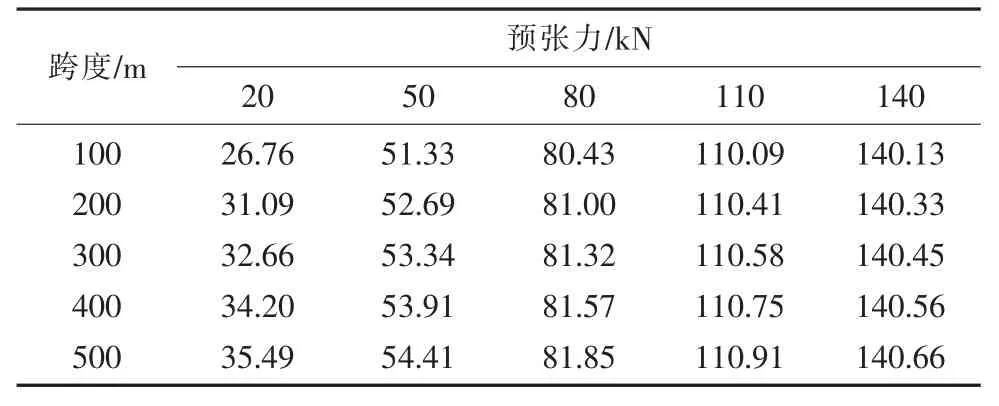
表1 封网承力索最大轴力

式中：Fm，Fp分别为承力索最大轴力及初始预张力。由图14 可知，随着预张力的增加，承力索最大轴力增量百分比逐渐减小。随着跨度的增加，增量百分比逐渐增加。当承力索预张力达80 kN及以上时，轴力增量百分比均小于3%，即当封网承力索预张力达80 kN 时，可不考虑高速列车及自然风耦合风荷载对承力索轴力的影响。

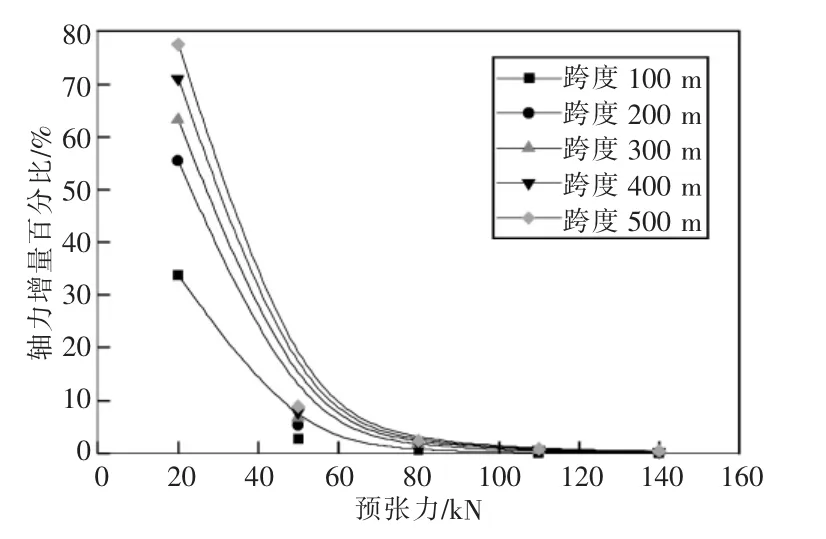
图14 承力索轴力增量百分比

不同预张力及跨度下，封网承力索的水平风偏如图15 所示。由图15 可知，随着承力索预张力的增加，封网水平风偏减小。当承力索与预张拉力大于80 kN 时，封网水平风偏趋于稳定。预张力为80 kN 时，跨度为500 m 的封网水平风偏为0.62 m。当跨度较大时，需采取增大预张力或限位拉索等措施降低封网水平风偏值。

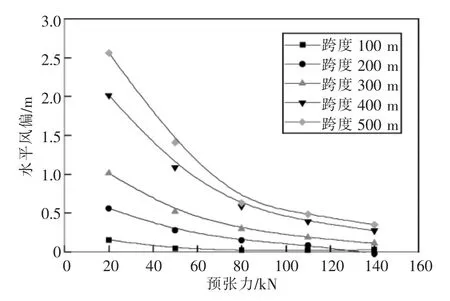
图15 封网横向水平风偏与预张力关系曲线

不同参数下，封网竖直风偏如图16 所示。由图16 可知，预张力可有效减小封网的竖向风偏值。对于向下风偏响应，大于80 kN 的预张力能有效抑制该响应。封网发生向上风偏时，其长度缩短、预张力减小。故承力索预张力对封网向上风偏的抑制作用小于向下风偏的抑制作用。随着跨度增加，封网风偏响应逐渐增加。当跨度为500 m 的封网预张拉力为80 kN 时，其向上、向下风偏最大值分别为3.53 m 及1.65 m。当封网安装塔架及承力索强度满足要求时，封网预张拉力不宜小于80 kN。

图16 封网竖直风偏与预张力关系曲线

3.2 封网安装高度及角度的影响

由图6 可知，列车运行时，不同高度的最大风速不同。对于第2 节算例中的封网，距离车顶不同高度时，封网中部承力索最大张力如图17所示。由图17 可知，随着封网承力索距离列车车顶高度的增加，封网的轴力逐渐减小。但由于封网结构较柔，其承力索轴力主要由初始预拉力控制，此结论与表1 结论一致。本节分析了60°，75°及90°情形下封网承力索的轴力响应。考虑列车风耦合作用后，耦合风荷载风攻角发生变化。当封网夹角与列车行进角度呈60°时，承力索轴力出现最大值。

图17 承力索轴力与封网高度安装关系曲线

不同安装高度下，封网承力索水平及竖直风偏如图18 所示。不同高度及安装角度下，封网水平风偏较接近。由于自然风风速较列车风大，当封网与列车前行方向夹角为90°时，封网的横向水平风偏最大。封网安装高度对封网水平横向风偏的影响较小。随着封网安装高度增加，封网水平横向风偏先增后减，在高度为11 m 时出现最大值。随着安装高度变化，列车风在水平及数值三方向的风速均发生改变，致使耦合风在空间中的风攻角略有变化，继而造成随高度增加，封网承力索水平风偏呈先增后减趋势。

图18 封网横向水平风偏与安装高度关系曲线

不同安装高度下，封网在数值方向风偏如图19 所示。由图19 可知，安装高度对封网结构在数值方向的风偏影响较小。随着安装高度的增加，列车风对封网结构的影响降低，封网结构在竖直向上方向的风偏逐渐减小。当安装高度距离列车车顶超过10 m 时，安装高度的影响趋于平稳。由于列车在封网下部运行，由图6 可知，竖直方向上，列车风向上分量大于向下分量，列车风对封网结构有一定升力作用。该升力作用能有效减小封网的向下风偏。当封网结构跨度为300 m、承力索预张力为80 kN 时，封网在数值方向运动范围为-1.18～1.45 m。在进行施工设计时，应注意封网的上下振动范围，避免封网对高速列车接触网及上部施工线路的影响。由于封网结构在数值方向上存在封网与列车前行方向夹角为60°时，耦合风荷载升力大于夹角为90°时的升力，夹角为60°时封网向上风偏距离大于90°夹角时的响应值。该升力也使60°时封网向下风偏的距离更小。