基于频响函数曲率的高压电力电缆护套结构损伤定位

杨世迎，陈晓儒，黄龙毅，于是乎，钟万里，张 锋，钟森淼，钟红梅，邓小康，朱 双

（1.广东电网有限责任公司惠州供电局，广东 惠州 516001；2.广东电网有限责任公司电力科学研究院，广州 510000）

0 引言

随着经济高速发展和城市化进程的不断推进，电力电缆因节约城市用地、环境友好等优点在国内外城市输配电网建设中得到了广泛应用，据中国南方电网公司电力电缆故障情况统计数据，发生的百余起110 kV 及以上电力电缆故障中，由外力破坏造成故障占到了七成以上[1-3]。有相关学者研究发现高压交联聚乙烯电缆长期在振动环境中运行时将导致绝缘结构疲劳损坏，绝缘外部电缆护套由于荷载效应、外部冲击等原因，使地下电缆更容易遭受破坏，多数事故的发生都是由于电力电缆结构损伤所引起的[4-7]。为预防地下电力电缆破坏出现，须全面考虑影响电力电缆安全性因素，确保电缆安全运行[8-10]。

针对电力电缆护套结构方面的损伤研究并不多见。因此有必要对电力电缆护套结构进行损伤识别与评估。目前研究电缆护套结构损伤方面多数为护套受环境应力开裂的影响造成其供电中断，然而现实情况是影响其供电中断的主要原因是电缆护套受到外部冲击造成的护套凹陷。有学者利用频响函数等作为损伤因子来进行机械结构动载荷损伤识别的分析，相关学者利用频响函数曲率对一个真实桥梁结构进行多阶段分区域动力测试的损伤评估，还有学者利用频响函数曲率对锚杆进行损伤位置的识别的研究。结果也表明，利用频响函数的曲率可以对结构进行有效的损伤识别。

本文对地下电力电缆护套结构损伤进行分析，对不同工况下的电力电缆护套进行结构振动试验，精确其损伤严重程度。通过动力试验对电力电缆护套实现无损检测，避免耐压试验等破坏性试验对电力电缆护套的损伤，延长电缆的使用寿命。

1 理论研究

为研究电力电缆护套出现的结构性损伤，构建电力电缆护套结构振动损伤数学模型。分析电力电缆结构受力过大会造成电力电缆护套产生凹陷或者损坏原因，对电力电缆护套进行结构频响函数曲率识别。

1.1 护套结构振动损伤数学模型

实际电缆敷设过程中，护套随时受到挤压等受力过大原因造成的电缆凹陷，护套凹陷过深最终会导致护套内部绝缘电场分布不均，造成绝缘击穿，影响供电可靠性，相关现场电缆敷设发现，护套凹陷0.8 mm 时，会造成供电中断等不利因素，电力电缆护套凹陷产生结构性损伤，即电力电缆护套截面惯性矩减小，电力电缆护套无凹陷情况下的截面惯性矩见式（1）：

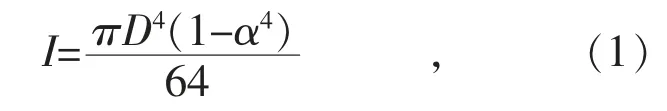
式中：α=d/D（d 为内环直径，D 为外环直径）。

电缆护套凹陷0.8 mm 的截面惯性矩见式（2）：

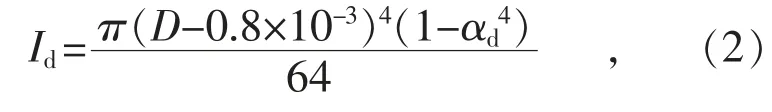
弯曲是电力电缆护套在垂直于轴线方向上振动时的主要形变[11-17]。由各力对垂直xy 平面的平衡方程以及达朗贝尔原理，完好的电力电缆护套结构以及凹陷损伤电力电缆护套结构的横向振动损伤数学模型见式（3）、式（4）：

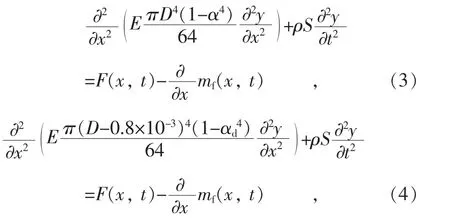
式中：F（x，t）为电力电缆护套上分布的外力；mf（x，t）为电力电缆护套上分布的外力矩；ρ 为电力电缆护套的密度；S 为电力电缆护套的横截面积；E 为电力电缆护套的弹性模量。

令F（x，t）=0，mf（x，t）=0，E、I 为定值，有完好电力电缆护套结构横向自由振动数学模型式（5）以及有凹陷损伤电力电缆护套结构的横向自由振动数学模型式（6）：

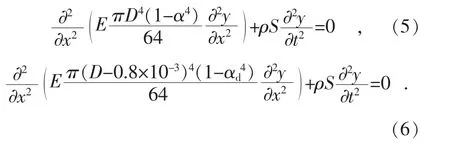
1.2 护套结构频响函数分析

电力电缆护套结构受迫振动方程见式（7）：

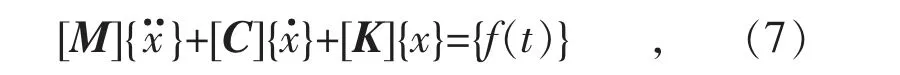
式中：矩阵[M]，[C]，[K]分别为振动结构的质量、阻尼和刚度矩阵。与各矩阵相对应的分别为振动结构响应加速度、速度和位移列阵，f（t）是振动结构激励。

式（7）两边进行拉氏变换，得式（8）：

式（8）进行拉式变换，得式（9）：

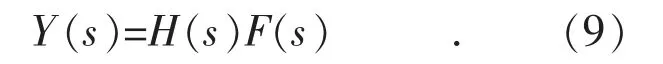
式（9）进行分式变换，得式（10）：

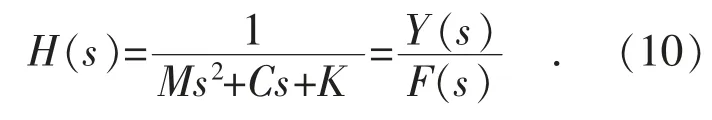
令S=jω，将拉式变换变成傅立叶变换，则有频响函数式（11）：

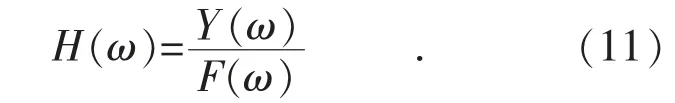
1.3 护套频响函数曲率分析

设结构j 点作用有输入激振力为Fj，任意点i处的输出响应为Xi，将输出响应与输入激励力比值定义为频响函数，见式（12）：

式（12）中的Hij（ω）定义i，j 之间的频响函数，即电力电缆护套结构在j 点处施加激励，点i 处所引起的响应。由电力电缆护套结构获得的输入和输出量，通过分析计算后，获得电力电缆护套结构的频响函数。即电力电缆护套结构的输出量与输入量之比。外界激励频率ω 作为频响函数参数量的非参数模型。

以频响函数的曲率作为结构损伤的识别参数，基于电力电缆护套损伤结构和未损结构的曲率变化进行识别。此曲率利用中心差分的方法得到，损伤前后的电力电缆护套结构曲率计算见式（13）、式（14）：

2 试验研究

对不同工况的结构损伤电力电缆护套与完好情况的电力电缆护套进行分析，针对电缆护套凹陷出现的结构性损伤，开展了结构振动试验，针对不同工况的电力电缆护套结构，通过测得的激励信号及响应信号，进行电力电缆护套结构的频响函数分析，判断完好情况及不同损伤程度电力电缆护套频响函数的大小。分析利用频响函数判别电缆护套结构性损伤特性的可行依据。

2.1 振动试验分析

结构振动试验对电力电缆护套进行损伤判断不会损伤电缆本体。结构振动试验中，频响函数可直接测得，便于结构性损伤检测。

试验模型为一段电力电缆护套，此110 kV电力电缆外力破坏线路截取为交联聚乙烯高压电缆线路，型号为YJLW03-Z 64/110 单芯，电缆导体截面积为400 mm2，长度为1.2 m。外护套材料为PE，弹性模量E=0.9×109Pa，密度为950 kg/m3，泊松比为0.38。

图1 所示试验采用力锤对电力电缆护套施加冲击力。

图1 振动试验接线

将电力电缆护套固定于两端支座上，依次对电力电缆护套设置编号。编号从左到右依次为1，2，…，7。试验利用电缆挤压机，将电力电缆护套设定为无损伤、电力电缆护套凹陷0.02 mm、电力电缆护套凹陷0.2 mm、电力电缆护套凹陷0.8 mm 四种工况，采用美国晶钻仪器公司的Spider-80X 动态信号采集及分析系统、美国PCB公司的加速度传感器拾取结构的动态响应，加速度传感器紧紧贴在第5 节点处，保证加速度传感器和电力电缆护套节点的响应保持一致。使用086C03 型力锤对电力电缆护套施加激励，Spider-80X 动态信号采集及分析系统，进行加速度信号和力信号的采集，并将采集信号数据进行储存。分析频率设置为900 Hz。

2.2 频响函数识别与分析

图2 是试验采集到的敲击完好护套第一点的冲击力时程和傅立叶谱图，图2（a）显示采集到的敲击第一点的正常冲击力。图2（b）显示采集到的敲击第一点的傅立叶谱图。

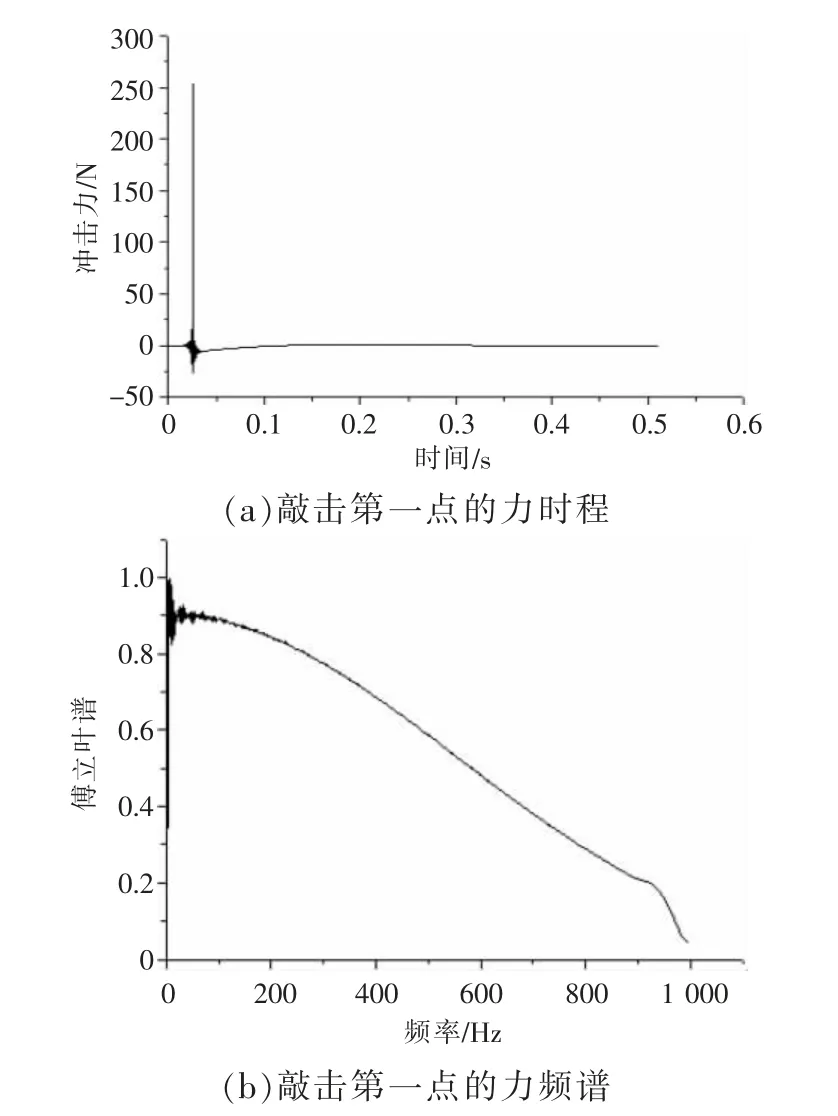
图2 敲击第一点的力时程与力频谱

激励信号的时域历程及激励信号的频谱，该信号为输入信号。激励信号的好坏直接影响最终结果，一般衰减不大于20 dB。

估算频响函数在单点输入力的作用下，本试验计算频响曲线选择Hv 法（多输入多输出估计法）。针对电力电缆护套结构振动试验选择Hv 法进行频响函数的计算。利用相干函数判别频响函数的优劣性。通过式（8）和式（9）得到某一测点的输入信号F（S）和输出信号Y（S），计算该测点的频响函数及相干函数，利用相干函数对频响函数质量进行检验，如图3 所示。

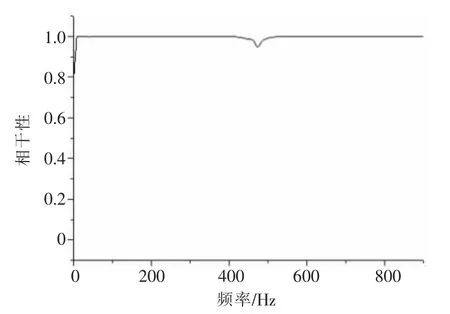
图3 频响函数的相干性检验

相干函数数值若接近于1，表明激励和响应间有着良好的相干性；若相干函数较小，则表明激励和响应间的相干性不好。相干系数大于等于0.8 时，表明频响函数的质量是可靠的，由图4可知相干性接近1，表明测试质量良好。

PC 实时测试软件获得了电力电缆护套结构无损伤、电力电缆护套结构凹陷0.02 mm、电力电缆护套结构凹陷0.2 mm、电力电缆护套结构凹陷0.8 mm 四种工况下的频响函数。由输入、输出信号可以判别电力电缆护套结构无损伤、电力电缆护套结构凹陷0.02 mm、电力电缆护套结构凹陷0.2 mm、电力电缆护套结构凹陷0.8 mm 四种工况下的频响函数。四种工况下的频响函数，见图4、图5、图6、图7。

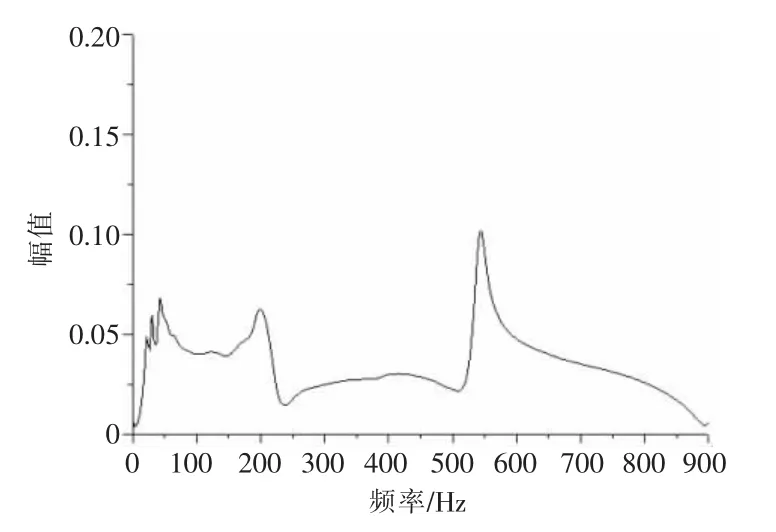
图4 完好护套下的频响函数

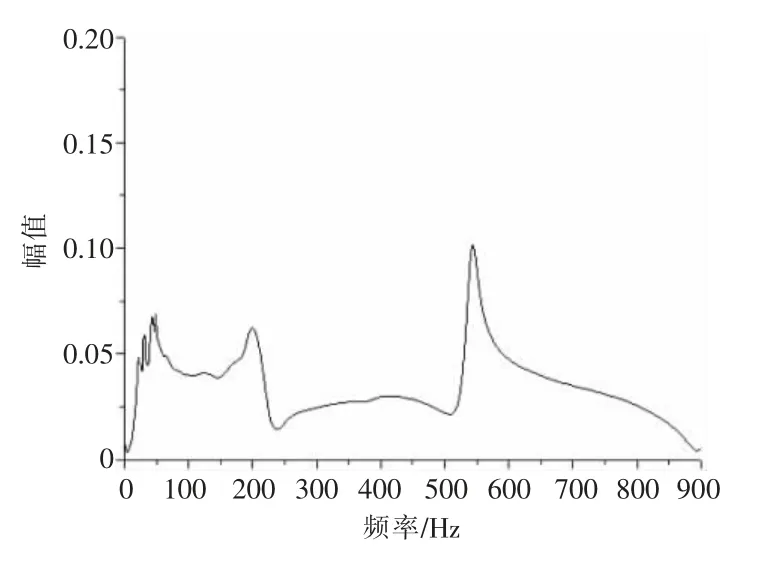
图5 护套凹陷0.02 mm 频响函数

由图4、图5、图6、图7，完好电力电缆护套频响函数峰值为0.109，电力电缆护套凹陷0.02 mm 情况下，频响函数峰值为0.112。完好电力电缆护套频响函数峰值与电力电缆护套凹陷0.02 mm 频响函数峰值仅相差0.003，是由于电力电缆护套凹陷深度较低，电力电缆护套凹陷0.02 mm 的频响函数与完好电力电缆护套情况下的频响函数峰值基本无差别，当电力电缆护套凹陷0.2 mm 时，其频响函数峰值为0.39，电力电缆护套凹陷0.8 mm 时，其频响函数峰值为0.61。由频响函数判别电力电缆护套结构性损伤具备可行性。

图6 护套凹陷0.2 mm 的频响函数

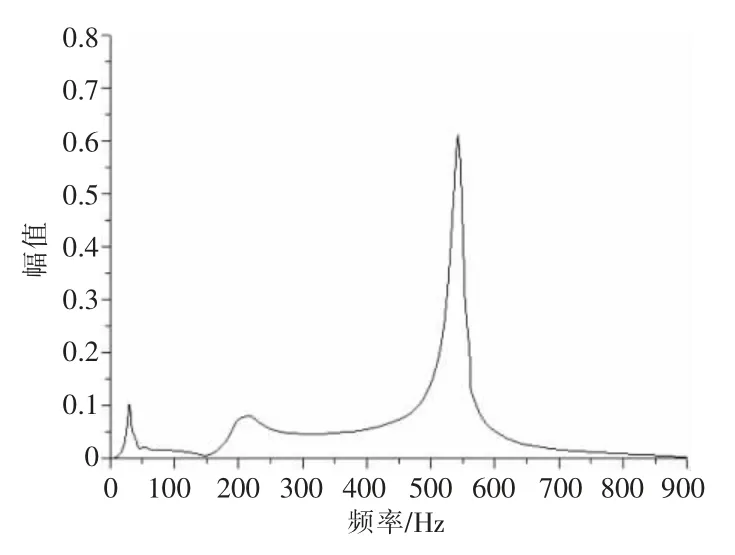
图7 护套凹陷0.8 mm 的频响函数

2.3 频响函数曲率损伤识别研究

对电力电缆护套进行损伤检测时，频响函数可作为诊断损伤的特征参数，但其缺点是无法反映出位置信息，进行损伤检测时必须进行适当变换，将其和位置坐标相联系。把频率响应函数的曲率作为电力电缆护套结构损伤识别的参数，基于电力电缆护套结构损伤部位和电力电缆护套结构没有损伤的部位的曲率振幅特征参数变化来区分完好电力电缆护套和凹陷的电力电缆护套，通过对电力电缆护套进行锤击试验，电力电缆护套结构曲率由中心差分的方法得到。根据电力电缆护套结构完好、电力电缆护套结构凹陷0.02 mm、电力电缆护套结构凹陷0.2 mm、电力电缆护套结构凹陷0.8 mm 四种工况下的电力电缆护套结构频响函数计算出四种工况下的电力电缆护套结构频响函数曲率（见图8）。

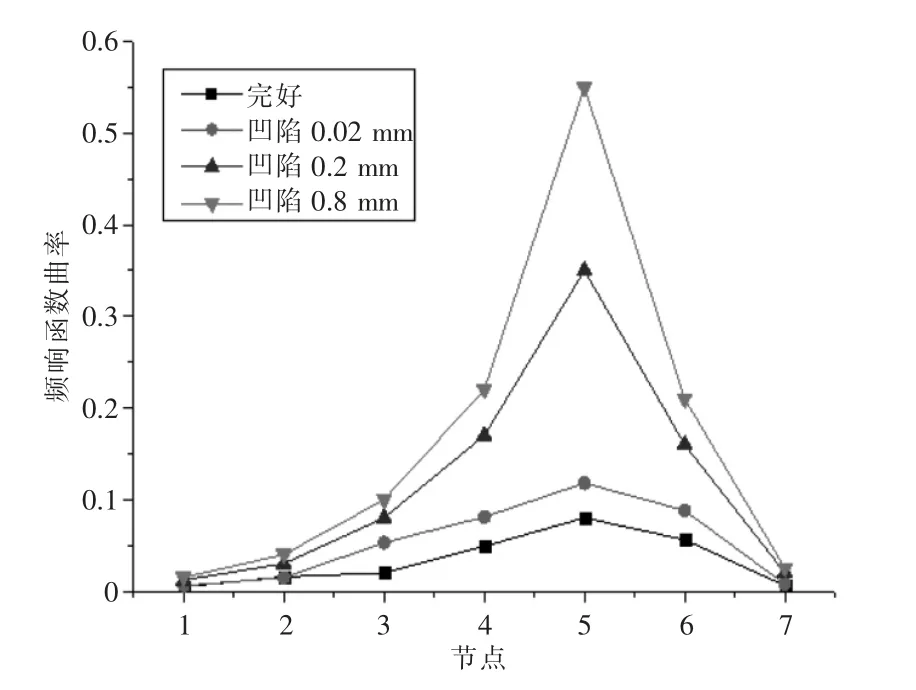
图8 电缆护套各工况下的频响函数曲率

单处凹陷的频响函数通过计算得出单处凹陷的频响函数曲率。图8 为电缆护套受到外部冲击，产生0.02 mm、0.2 mm、0.8 mm 凹陷的频响函数曲率，随着电缆护套凹陷损伤程度的增大，频响函数曲率也在随之增大，在损伤位置处有明显的峰值，通过频响函数曲率变化判断电缆护套结构损伤位置。

通过锤击法测试，分析电缆护套结构完好工况及损伤工况频响函数曲率大小，发现随着损伤程度增大，损伤节点的频响函数曲率峰值也增大，当损伤处凹陷为0.8 mm 时，对应的频响函数曲率数值为0.55，针对电缆结构损伤可有效识别。

3 结论

本文针对电力电缆护套结构性损伤特性进行了研究。电力电缆护套结构损伤主要为凹陷损伤；建立了电力电缆护套凹陷损伤的结构振动损伤数学模型，针对电力电缆护套结构损伤特性以及对电缆护套凹陷产生绝缘凹陷损伤特性进行试验。结论如下：

1）电缆护套凹陷导致电缆绝缘结构损伤，绝缘有效承载面积减小。电缆护套结构出现凹陷结构性损伤，其截面惯性矩减小。

2）研究不同凹陷工况对电缆结构性损伤的影响，对电缆护套进行了振动试验，对不同损伤工况的电缆护套进行频响函数分析，电缆护套完好情况，频响函数峰值为0.163，电缆护套达到供电中断的0.8 mm 凹陷时，其频响函数峰值为0.61。将频响函数曲率作为电缆护套结构损伤参数，由频响函数曲率可知，随着电缆护套凹陷损伤程度的增大，频响函数曲率也在随之增大，5节点峰值由完好电缆护套的0.082 到5 节点电缆护套凹陷0.8 mm 时峰值0.55，对电缆护套损伤可进行有效定位。