空间荷载作用下某异型钢筋混凝土棚洞结构仿真分析与优化设计

陈 诚，王 建，黄 鹏

（中国电建集团成都勘测设计研究院有限公司，四川 成都 610072）

0 前 言

我国西部地区（特别是西南地区）地势险要、山岭密集、地震断裂带发育，在此区域的交通工程建设必须考虑落石的影响［1］。其中，隧道作为山区公路的交通核心，其洞口构筑物（棚洞、拱形明洞、简易护棚等）的安全性、可靠性、耐久性就显得极为重要。

常见的钢筋混凝土棚洞为简支梁板柱结构，属于隧道明洞范畴，对隧道洞口落石、防冲击有很好的针对性。采用棚洞的条件与明洞大致相似，其结构整体性比拱形明洞差，但由于顶棚与内外墙简支，结构自重较轻，即对地基承载力的要求相对较低，另外其结构型式可依功能性变化调整［2］。因此，如何设计出既能够满足功能要求又可以尽可能考虑经济性的钢筋混凝土异型棚洞，即是本文的研究主题。

1 工程背景

1.1 工程概况

本文以国内某大型水电站进场交通隧道洞口钢筋混凝土异型棚洞的结构设计为例，该工程设计速度30 km/h，路基宽度8.5 m，洞口设计高程为2 373.88 m。棚洞与隧道洞口顺接，采用框架式现浇钢筋混凝土结构，洞（净）跨9 m，洞（净）高6.8 m。

1.2 工程地质条件

洞口段为覆盖层，地势较平缓，地形坡度约15°，覆盖层垂直厚度约6～8 m，水平厚度15～28 m，主要由崩坡积块碎石土构成，结构较松散。洞口顶部高28 m内地势呈起伏状，整体坡度23°，最大坡度35°。工区岩性以中厚层砂岩为主，夹板岩及千枚岩，强卸荷深度达35 m，优势节理较少，岩层产状同洞轴线方向大角度相交。

1.3 覆盖层力学参数

现场试验选取覆盖层物理力学参数，并根据本工程各土层基本特性，结合已建工程经验进行工程地质类比综合分析确定。按照有关规程要求，渗透系数以现场抽水、注水试验的大值平均值作为标准值；抗剪强度指标、土层允许承载力按重力触探锤击数与其相关经验公式给定。土层物理力学参数见表1。

表1 覆盖层物理力学参数

1.4 岩体力学参数

该段基岩以中厚层砂岩为主，夹板岩及千枚岩。砂岩类属坚硬岩，板岩属中硬岩，千枚岩属软岩。因岩性的不同组合，往往造成岩体强度的差异，总体上各层的划分反映了不同岩性的组合，但因其相变较大，难以分层评价，故以主要岩性和岩体风化程度进行工程岩组划分并予以评价。岩体物理力学参数见表2。

表2 岩体物理力学参数

2 理论依据

国内外大多数学者对钢筋混凝土异型棚洞结构的设计研究方式趋同，主要采用经验类比法以及简化受力的理论计算法，或是采用平面有限元结构荷载模型进行受力分析。

混凝土材料在受拉或受压时，表现出不同的受力性能和损伤状态。为了更好描述混凝土材料在受拉、受压状态下的差异，科学家们做出了大量的努力。1871年，Levy将塑性应力-应变关系推广到三维情况［3］；1913年，Mises经数学简化提出了Mises屈服条件；Mises还独立地提出和Levy一致的Levy-Mises塑性应力-应变（本构）关系［4］。1924年，Ilyushin等苏联学者提出塑性全量理论，用来解决了大量实际问题。1930年，Reuss在Prandtle的启示下，提出包括弹性应变部分的三维塑性应力-应变关系［5］。至此，塑性增量理论初步建立。1950年前后，学术界展开了塑性增量理论和塑性全量理论的辩论，促使对两种理论从根本上进行探讨。二十世纪七十年代，随着有限元方法的提出和快速发展，关于塑性本构关系的研究十分活跃，主要从宏观与微观结合的角度，从不可逆过程热力学以及从理性力学等方面进行研究，例如无屈服面理论等。Jeeho Lee等［6］在后期修正了Lubliner等在1989年提出的屈服方程，使用多硬化屈服方程来描述屈服面的演化过程［7］。

ABAQUS有限元仿真模拟软件被广泛地认为是功能最强的有限元软件，可以分析固体力学中复杂的结构力学系统，特别是能够驾驭非常庞大复杂的问题和模拟高度非线性问题。

本文以工程实例设计为背景，采用ABAQUS进行三维有限元数值分析，建立了各向同性的混凝土塑性损伤实体模型，并分析了该棚洞结构的荷载响应，对计算出的结果进行了正面验证，再以计算结果为依据，对该钢筋混凝土异型棚洞结构配筋进行了适当优化设计。

3 数值计算模型

棚洞建筑限界为7.5 m×5 m（宽×高），设计速度30 km/h，采用框架式现浇钢筋混凝土结构，洞跨9 m，洞高6.8 m；临空侧边墙设有一门洞开口，宽度3.5 m，高度4 m；采用条形扩大基础。

为了方便将计算结果与所采用的材料强度参数进行对比，以及提高模型、计算结果的可视化程度，该次计算采用三维实体单元建模，效果如图1～2所示。棚洞结构仿真模型材料为C30钢筋混凝土。其具体参数见表3。

表3 模型选取的物理力学参数

图1 模型正向

图2 模型侧向

该钢筋混凝土异型棚洞结构设计荷载（见图3～4）指标如下：

图3 一般截面设计 （单位：cm）

F1：顶部土石回填与黏土隔水层自重（计算高度2 m）；

F2：C15片石混凝土自重（计算高度10 m）；

F3：C15片石混凝土与预计的塌落土石产生的侧向压力（计算高度15 m）；

F4：预计的塌落土石（计算高度50 m）；

G：棚洞结构自重，g。

其中，塌落土石荷载P根据现行业规范公式计算得出。由于棚洞设置有缓冲层，因此需将冲击荷载P（点荷载）按照棚洞顶板面积等效转换为均布荷载F4施加在棚洞结构顶板，冲击荷载P计算公式：

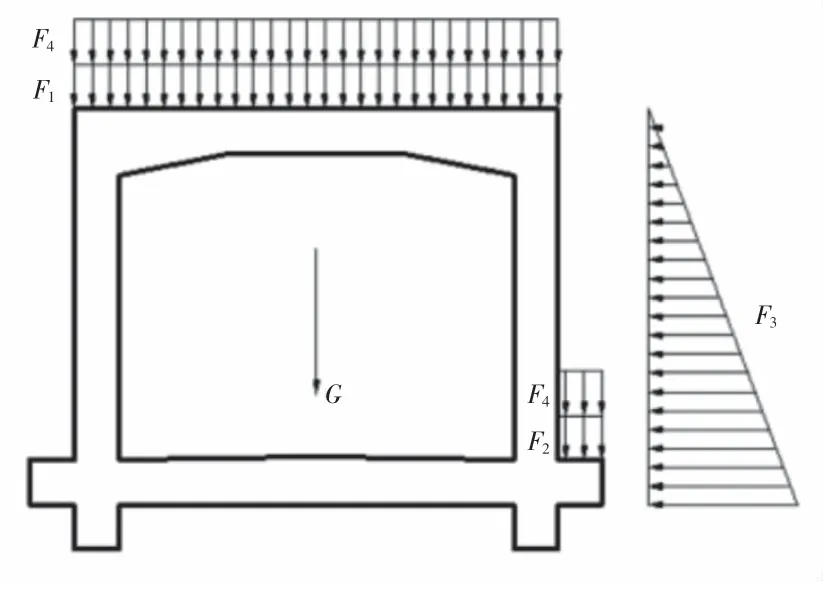
图4 一般截面荷载施加示意

该次计算F1、F2、F4采用均布荷载形式；F3采用静水压力荷载形式；G采用自重荷载形式。

边界条件的设定如下：

（1）原设计采用扩大基础，认为结构底部无转角或位移，采用刚性固定；

（2）原设计地勘资料显示，棚洞底部出露较稳定基岩，认为地基无沉降、无蓄水影响；

（3）为考虑研究分析的通用性，本文未考虑地震、暴雨、边坡失稳等极端工况。

4 结构荷载响应分析

该次计算采用各向同性的弹塑性实体单元建模，以C30混凝土物理力学参数赋值，对计算出的结果进行正面验证、分析，再以计算结果为依据，反算配筋量。

4.1 结构应力分析

由结构整体应力云图（见图5）可知，结构较大部分区域已处于中亮应力状态（中亮幅值域：1.3～2.5 MPa），部分大于C30混凝土的抗拉强度；侧边门洞顶部出现高亮应力集中现象（高亮幅值域：2.8～3.4 MPa），大于C30混凝土的抗拉强度。因此，从结构应力状态的角度讲，该结构设计是不可靠的，材料会发生明显的拉裂破坏，需配置相应的钢筋骨架，增强结构抗拉强度。

图5 结构整体应力云图（单位：Pa）

4.2 结构塑性应变分析

由结构整体塑性应变云图（见图6）可知，暗色区域为未发生塑性应变，即PE=0，中亮、高亮区域为已发生塑性应变，该区域主要集中在结构拐角、侧边门洞顶部等纵向延伸。因此，从结构应变状态的角度来讲，该结构设计是不可靠的，会发生上覆荷载造成的塑性破坏，即混凝土开裂，需配置相应的钢筋骨架，增强结构的刚度。

图6 结构整体塑性应变云图

4.3 结构位移分析

由结构竖直方向位移云图（见图7）可知，结构位移从上到下分布基本均匀，其中侧边门洞端幅值较大，暗色区域值域为6.6～7.9 mm，此为两侧边墙受侧压力发生的变形导致结构顶部位移。因此，从结构位移状态的角度来讲，该结构设计是不可靠的，边墙会发生侧向土压力引起的变形，需配置相应的钢筋骨架，增强结构的刚度。

图7 结构竖直方向位移云图（单位：m）

通过对结构在该常规工况的应力、应变、位移分析可知，未配置钢筋骨架是明显不可靠的，因此需提取最不利截面上的弯矩、内力进行结构整体配筋计算。

5 最不利截面内力计算

为寻找最不利截面，可提取Mises应力云图对结构整体受力状态进行分析。

Von Mises准则是Von Mises于1913年提出的一个屈服准则。Von Mises准则是一个综合的概念，其考虑了第一、第二、第三主应力，可以用来对疲劳、破坏等的评价。当某一点应力应变状态的等效应力应变达到某一与应力应变状态有关的定值时，材料就屈服。

Mises应力是一种折算应力，折算依据为能量强度理论，即第四强度理论。计算公式形式简单，但结果偏保守，因此可根据云图应力集中（深色应力）部位找到所需截面，排除网格剖分异形处造成的应力集中干扰，可选取如下截面（见图8）。

图8 选取计算截面

提取该截面全部的节点内力，经后处理可得出该截面合力如下：

合力矩：M=2.679×106N·m；

合轴力：N=2.812×106N；

合剪力：V=2.634×106N。

得到了最不利截面的各项内力后，可按照钢筋混凝土结构设计原理及相关规范对该棚洞结构进行配筋验算。

6 结构优化设计

按照钢筋混凝土原理及《混凝土结构设计规范》要求，结构配筋计算主要包括正截面承载力、斜截面承载力、裂缝宽度三方面［8］。

6.1 正截面承载力

在正截面优化设计中，根据原设计参数，采用双筋梁受力模式，建立基本计算公式如下：

将纵向受拉钢筋As分解为As1和As2，As1与受压区混凝土形成单筋矩形截面梁关系，抵抗弯矩为Mu1；As2与受压钢筋抵抗弯矩为Mu2。二者抵抗弯矩之和即为双筋矩形截面梁的抗弯能力设计值Mu。建立计算公式如下：

通过仿真分析得出截面弯矩设计值M=2.679×106N·m，其中设定采用b=1 000 mm、h=1 500 mm的矩形梁截面形式。查表可知，混凝土强度等级fc=14.3×106N/m3，ft=1.43×106N/m3，fy=360×106N/m3，f′y=14.3×106N/m3，ξb=0.518；混凝土强度等级为C30，α1取值1.0。

为节约钢筋，充分发挥混凝土的抗压强度，假定ξ=ξb，此处查阅相关论文文献，建议设计时取ξ=0.75ξb～0.80ξb。虽经济性稍差，但构件的力学性能可得到明显改善，尤其利于结构抗震，取ξ=0.75ξb=0.75×0.518=0.389。带入可得：

由设计图可知，该梁采用直径为28 mm的HRB400热轧带肋钢筋骨架，其单根截面面积为615.44 mm2，计算可知：受拉区钢筋根数为10根；受压区钢筋根数为5根。

对比可知：原设计中该梁截面受拉区钢筋采用间距15 mm、直径28 mm的热轧带肋钢筋24根；受压区钢筋采用间距150 mm、直径28 mm的热轧带肋钢筋6根。因此，原设计在正截面抗弯承载力理论验算的层面上是较保守的，可以进行优化设计。

6.2 斜截面承载力

影响梁斜截面抗剪承载力的因素很多，影响机理也很复杂，精确计算相当困难。通常采用半经验半理论的方法解决斜截面的抗剪承载力计算问题［8］。

在斜截面优化设计中，根据原设计参数，采用同时配置箍筋和弯起筋的梁，其斜截面抗剪承载力等于仅配箍筋梁的抗剪承载力与弯起钢筋抗剪承载力之和，即：

大学士所冠殿阁包括四殿二阁，分别是中极殿（旧名华盖殿）、建极殿（旧名谨身殿）、文华殿、武英殿、文渊阁、东阁。这些大学士都是正五品，地位较低。文华殿与太子有关，加大学士衔罕见。作为一种例外，曾有兼两殿阁大学士者。例如景泰七年五月，陈循兼华盖殿大学士和文渊阁大学士，高榖、王文都兼谨身殿大学士和东阁大学士。大学士的本职在翰林院。自仁宗时，大学士不再入院理事。翰林院撤销了大学士的办公桌，引起抗议和皇帝的干涉［2］（卷73，职官二）。

根据工程实践经验及实验结果，为防止出现斜压破坏，并限制在使用荷载作用下斜裂缝的宽度，对矩形、T型、I型截面受弯构件设计时必须满足下列截面尺寸限制条件：

当梁的抗剪承载力不足时，需经计算确定腹筋数量，其中，需满足直径和间距的构造要求外，还需满足最小配筋率的要求：

通过仿真分析得出截面剪力设计值V=2.634×106N，其中设定采用b=1 000 mm、h=1 500 mm的矩形梁截面形式。

查表可知，混凝土强度等级fc=14.3×106N/m3，ft=1.43×106N/m3，fy=360×106N/m3，fyv=360×106N/m3，混凝土强度等级为C30，βc取值1.0。

该梁段箍筋选用双肢直径16 mm、间距150 mm的HRB400热轧带肋钢筋，带入可得：ρsv=0.27%，满足箍筋最小配筋率要求。

原设计中选用直径20 mm、间距150 mm、弯起筋弯起角度为45°的HRB400热轧带肋钢筋作为弯起筋，带入可得：Asb=1 611.42 m2，即：每延米弯起5根直径20 mm的HRB400热轧带肋钢筋。

对比可知：原设计中该梁截面选用双肢直径16 mm、间距150 mm的HRB400热轧带肋钢筋作为箍筋是足够的；原设计中该梁截面选用直径20 mm、间距150 mm的HRB400热轧带肋钢筋作为弯起筋，每延米弯起根数为6.67根。因此，原设计在斜截面抗剪承载力理论验算的层面上是较保守的，可以进行优化设计。

6.3 裂缝验算

影响裂缝宽度的主要因素包括：受拉钢筋应力、混凝土与钢筋之间的黏结力、混凝土保护层厚度、钢筋直径及其布置方式、混凝土强度、荷载作用性质、构件受力性质等［8］。

《公路桥规》给出的裂缝宽度计算公式如下：

查表可知，混凝土强度等级ftk=2.01×106N/m3，Es=2.01 MPa；采用C30混凝土；配置直径28 mm的HRB400热轧带肋钢筋24根；混凝土保护层厚度50 mm；按照二类环境考虑，裂缝宽度限制ωlim=0.2 mm，带入可得：应变不均匀系数ψ=0.64；考虑长期作用影响的最大裂缝宽度ωmax=0.15 mm≤ωlim，满足规范要求。

7 结论与建议

通过采用ABAQUS有限元仿真模拟软件对该异型钢筋混凝土棚洞结构在设定工况下的应力、应变、位移分析，建立各向同性的混凝土塑性损伤实体模型，同时提取出最不利截面上的弯矩、内力等，按照钢筋混凝土设计原理及《混凝土结构设计规范》要求，对设定的梁截面进行正截面承载力、斜截面承载力、裂缝宽度三方面验算，最终在理论层面将计算结果与原设计图纸中的相关参数进行对比分析，得出以下结论及展望。

（1）通过在设定工况下的结构荷载响应分析可知，该棚洞结构若未配置钢筋骨架是不可靠的。

（2）原设计中非开孔部位梁板配置的钢筋骨架偏保守，受拉主筋布置富余量较大，可以进行一定程度的优化设计。

（3）通过塑性应变仿真结果可知，在门洞开口侧墙与顶板交接处，存在较明显的纵向塑性变形，因此宜在该转角处设置纵向暗梁，以确保棚洞结构纵向刚度。

（4）通过位移仿真结果可知，在该工况条件下，结构受较大的侧向土压力，因此可根据计算结果进行适当加强内侧墙设计配筋；外侧墙因门洞开口形成了柱结构，其配筋设计应按柱式配筋考虑。

（5）该棚洞结构发生应力集中区域，即结构薄弱处主要出现在侧边门洞附近。在设定工况下的结构荷载响应时，侧边门洞附近产生较大的拉应力，在设计中应考虑在此位置布设加强孔口筋。

（6）混凝土塑性损伤本构模型能更好地模拟混凝土受拉、受压时的不同表现，能同时反映材料“硬化”与“软化”应力应变关系特点，以及混凝土的不可恢复变形等特性。

（7）将仿真计算分析与理论公式计算相结合，可较好地设计出既能够满足功能性要求又可考虑经济性的异型结构。

目前，国家对西部交通设施建设的投入越来越大。鉴于西部山区的特殊地形地貌，棚洞结构以其独特的优势将在未来大量应用西部公路建设中。随着公路建设的迅猛发展和建设规模提升，棚洞结构型式也需要不断创新和发展。未来公路工程建设中，尤其针对棚洞工程建设，需采用新技术、新工艺，通过采用先进的环境保护措施，来降低工程对生态的影响，同时棚洞结构无论从材料选用、断面大小及结构型式等都可以进行针对性的改进和创新。