无锡地铁整体硫化压缩型减振扣件段环境振动特性研究

苏 劼，马龙祥，汪 乐，李弘毅

(1.无锡地铁集团有限公司，江苏无锡 214100； 2.西南交通大学土木工程学院，成都 610031； 3.中设设计集团股份有限公司，南京 210014)

引言

随着我国轨道交通的快速发展，全国各地地铁里程迅速增长。地铁在为城市居民带来诸多便利的同时，其列车运行产生的振动对周边环境也产生了一定的负面影响[1-3]。因此，如何减少地铁列车引起的环境振动已成为地铁设计中备受重视的环节[4-5]。

近年来，国内众多学者对不同轨道配置条件下的地铁振动特性进行了研究。王志强等[6]针对GJ-Ⅲ型扣件地铁区段开展了现场测试，分析采用不同减振措施后地铁的振动特性及相应减振措施的减振效果，发现GJ-Ⅲ型扣件相对于DTVI2型扣件具有显著减振效果；冯青松等[7]对普通扣件和减振扣件下列车运行引发的地表振动进行现场实测与数值模拟分析，研究减振扣件的减振效果发现，采用减振扣件后，道床振动峰值降低且低频频段偏移，隧道壁上减振扣件在卓越频率范围内出现振动放大现象；李克飞等[8]对钢弹簧浮置板轨道进行现场测试，得出钢弹簧浮置板轨道对低频段振动衰减较高频段更差的结论；刘维宁等[9]对Ⅲ型与Ⅳ型轨道减振器扣件轨道的振动加速度进行了现场测试，发现他们的响应在300 Hz附近有明显放大现象，且车轨共振明显；翟辉等[10]通过有限元模拟研究了地铁钢弹簧浮置板段列车运行产生的地表低频响应，得出了地表低频竖向振动随距离增加衰减，且在轨道结构自然频率处取得最大值的结论。

国内外学者及相关工程人员对城市轨道交通中普遍使用的各种减振轨道的减振性能均开展了相关研究，卓有成效，为相关减振轨道的应用积累了大量经验。无锡地铁在现今普遍使用的压缩型扣件基础上，较为广泛地采用了一种我国自主研发的整体硫化压缩型减振扣件[11]作为环境振动敏感区段的地铁减振措施。虽然目前已有大量关于普通压缩型减振扣件地铁区段环境振动的研究，且对其减振性能已有较为深入的认识，但仍然缺乏针对无锡地铁新型整体硫化压缩型减振扣件应用情况下地铁区段环境振动特性的定量研究。在此背景下，针对无锡地铁整体硫化压缩型减振扣件轨道段，应用基于周期-无限结构理论的车轨动力耦合模型[12]及轨道-隧道-地层耦合系统的2.5维数值模型，系统分析了地铁列车在其上运行时诱发轨道、隧道及大地的振动响应规律，进而明确了整体硫化压缩型减振扣件地铁段的列车振动传播特性。研究成果可为新型整体硫化压缩型减振扣件在地铁减振中的应用提供一定参考。

1 无锡地铁整体硫化压缩型减振扣件

减振轨道在我国已有二十余年的应用经验，目前，为满足高等和特殊减振需求采用道床减振，而对于中等减振则采用扣件减振[13]。我国常用的地铁减振扣件分为剪切型扣件与压缩型扣件。剪切型扣件利用橡胶的剪切变形为扣件系统提供弹性，具有良好的减振效果，但容易导致钢轨发生不同程度的异常波磨，进而引起轮轨系统强烈振动及车辆与轨道零部件的疲劳破坏[14-16]。与剪切型扣件相对应，压缩型扣件利用橡胶的压缩变形为扣件系统提供弹性，已取得一定的减振效果，能较好地避免地铁运营中钢轨异常波磨的产生[16]。我国DT系列与GJ-Ⅲ型等未经整体硫化的普通压缩型减振扣件[17-18]以及LORD扣件等整体硫化的压缩型减振扣件[18]均得到了较多应用。相较于普通压缩型减振扣件，整体硫化压缩型减振扣件采用整体硫化弹性铁垫板结构，将弹性铁垫板中大部分橡胶与空气隔离，不仅具有弹性均匀、轨道平顺性好、使用寿命长等优点，还能为扣件系统提供更好的弹性，从而更为有效及稳定地降低列车运营产生的振动与噪声[19]。因此，整体硫化压缩型减振扣件在我国地铁线路中具有良好的应用前景。

目前，我国地铁中应用的整体硫化压缩型减振扣件仍以美国LORD扣件为主，而无锡地铁在满足与部分轨道部件互换通用的前提下，为缓解钢轨磨损并提高轨道平顺性，较为广泛地使用了一种我国自主研发的新型整体硫化压缩型减振扣件。该新型整体硫化压缩型减振扣件竖向刚度12 kN/mm，阻尼系数3×104N·s/m，其现场应用情况如图1[11]所示。关于该新型整体硫化压缩型减振扣件应用效果的定量研究还十分缺乏，因此，有必要对其应用的地铁环境振动特性进行专门研究。

图1 无锡地铁研发的整体硫化压缩型减振扣件[11]

2 依托工程概况及动力计算模型

以无锡地铁某区段为依托工程，研究地铁整体硫化压缩型减振扣件段的环境振动特性。该区段隧道埋深20 m，管片内径2.7 m，外径3.1 m，左右线中心距离17 m，地层自上到下依次为①1杂填土、③1黏土、③2粉质黏土夹砂质粉土、⑤1粉质黏土、⑥1黏土、⑥2黏土和⑦1粉质黏土。隧道埋置于⑥1黏土层中，地层及隧道结构的物理力学参数见表1。区段运行列车为6节编组B型车，运行速度为60 km/h。

为实现研究目的，同时兼顾计算效率，按以下两步骤分析地铁整体硫化压缩型减振扣件段的环境振动特性。首先，建立地铁车辆与整体硫化压缩型扣件轨道的垂向动力耦合模型，并输入轨道不平顺，以解算出地铁车辆在轨道上运行时产生的轮轨力；然后，建立研究区段轨道-隧道-地层耦合系统的2.5维数值模型，并输入第一步求得的轮轨力，将其施加于轨道上，以求解轨道-隧道-地层耦合系统的振动响应，从而获得运行列车引发环境振动的量值及传播规律。

地铁车辆在减振轨道上运行时产生的轮轨力采用基于周期-无限结构理论的车轨动力耦合模型来计算，轨道不平顺采用美国5级谱进行模拟。具体地，由于整体硫化压缩型减振扣件轨道为整体道床轨道，采用以扣件间距L为周期的单层离散支撑轨道模型来模拟，其中，钢轨被模拟为无限长Euler梁，整体硫化压缩型减振扣件被模拟为弹簧-阻尼元件。地铁列车的每节车辆采用由车体、2个转向架、4个轮对及连接它们的弹簧阻尼元件组成多刚体模型来模拟，共具有10个自由度。据此所建立的车轨动力耦合模型如图2所示。

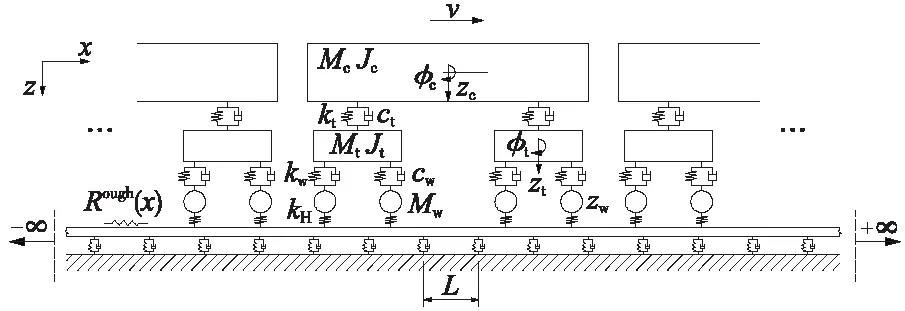
图2 普通整体道床单层轨道对应的车轨动力耦合模型

另一方面，轨道-隧道-地层系统则被视作沿线路纵向不变的一致性系统，采用2.5维数值方法进行模拟。其中，钢轨被视作Euler梁，采用2.5维解析法进行模拟，道床-隧道-地层系统被视作黏弹性空间体，采用2.5维有限元法进行模拟，动力计算边界采用2.5维人工黏弹性边界，钢轨与道床-隧道-地层系统通过扣件的力学平衡及位移协调条件进行耦合。与车轨动力耦合模型中采用离散支撑的弹簧阻尼单元模拟扣件不同，在2.5维模型中，扣件被模拟为连续支撑的弹簧阻尼单元，其相应参数可由单个扣件参数除以扣件间距得到。限于篇幅，此处不再对2.5维数值方法进行赘述，其相关计算原理可参考文献[20-21]。

针对研究区段所建立的2.5维轨道-隧道-地层耦合模型如图3所示。该模型在宽度上取120 m，深度方向上取80 m，列车荷载在右侧隧道进行加载。此外，在研究地铁诱发振动在大地中的传播时，着重研究右侧隧道(列车荷载加载侧隧道)右侧大地范围内的传播规律，因此，模型在右隧道右侧的区域更为宽阔。右隧道中线距模型左右边界的距离分别为48.5 m和71.5 m。

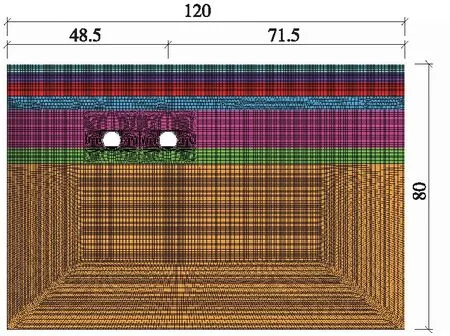
图3 轨道-隧道-地层耦合模型(单位：m)

3 振动响应分析

为研究地铁列车运行引发的振动传播规律，对线路同一横断面上钢轨、道床、隧道壁及地表不同位置处的竖向振动加速度响应进行研究。其中，钢轨响应以右隧道(加载隧道)右轨为例进行分析，道床拾振点选取在道床顶面的中心位置处，隧道壁拾振点选取在隧道壁右侧距道床1.5 m高的位置，而地表拾振点则在右隧道正上方地表位置向右50 m范围内每隔5 m选取1个。各拾振点的位置示意如图4所示。

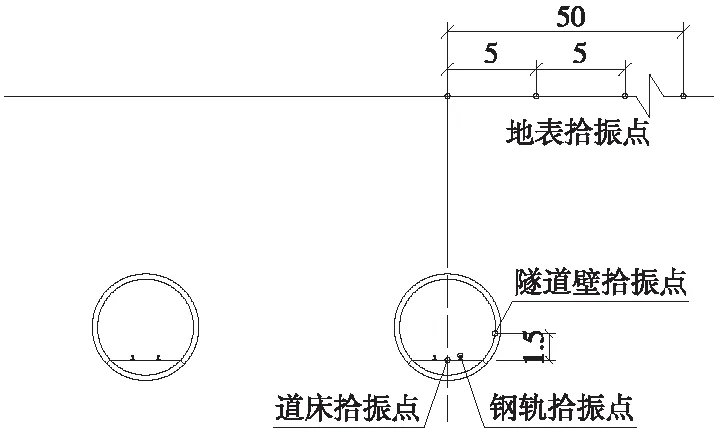
图4 拾振点示意(单位：m)

图5给出了钢轨、道床及隧道壁拾振点的1/3倍频程谱及不同点间的振动传递损失，包括道床相对于钢轨以及隧道壁相对于道床的分频振级传递损失。

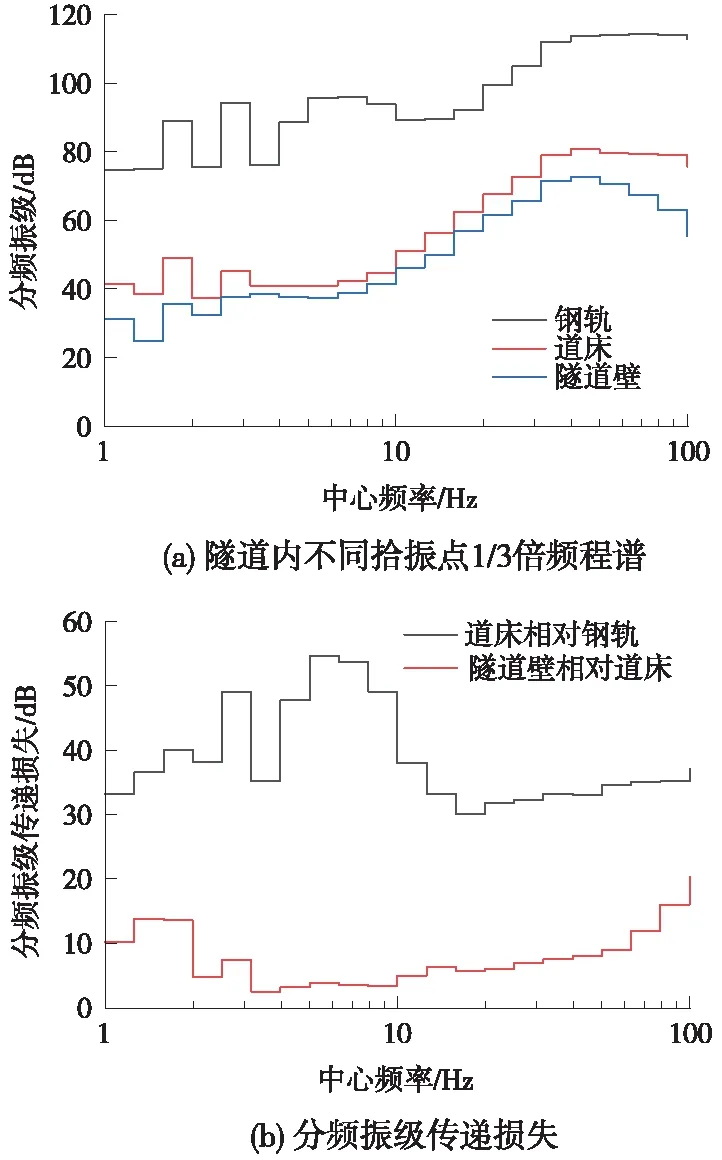
图5 隧道内拾振点1/3倍频程谱及分频振级传递损失

由图5可以发现，运行列车产生的1～100 Hz频段内的振动，从钢轨到道床，再到隧道壁呈逐渐衰减趋势，其中，钢轨拾振点的振动加速度级量值在74.6～114.3 dB内，而道床及隧道壁的振动加速度级量值分别在37.3～80.7 dB及24.8～72.7 dB内。振动在从钢轨至道床的传递过程中，分频振级传递损失在中心频率5 Hz达到最大值54.6 dB，且各频段的传递损失都在30 dB以上；而振动在从道床传递至隧道壁过程中发生的分频振级传递损失在中心频率100 Hz达到最值20.3 dB，且1～2 Hz与63～100 Hz频段的传递损失也都在10 dB以上。

表2给出了钢轨、道床及隧道壁拾振点的最大Z振级VLzmax及道床与隧道壁拾振点相对于钢轨的最大Z振级传递损失ΔVLzmax。从表2也可以看出，经过整体硫化压缩型减振扣件对振动的衰减后，道床及隧道壁的振动响应相较于钢轨都会有大幅衰减，他们相对于钢轨的最大Z振级传递损失分别达34.4 dB及42.9 dB。

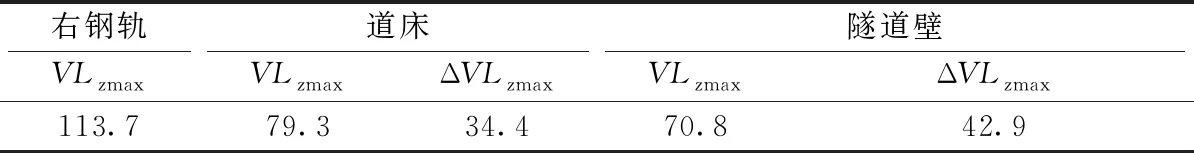
表2 不同拾振点最大Z振级及相对钢轨的传递损失

图6给出了运行列车引起的地表典型位置拾振点的加速度响应时程及频谱。从图6可以看出：运行列车诱发的地表加速度响应时程图像呈梭形，即随着列车驶近、到达及驶离拾振点的过程，地表加速度响应总体呈先增大后减小的趋势；在地表0，25，50 m处加速度响应时程的峰值分别为0.015 3，0.014 8，0.006 1 m/s2，表现出较为明显的随距离衰减的趋势；地表加速度响应主要集中在20～80 Hz频段，且由轮轨共振频率决定的响应频谱峰值均出现在30～50 Hz频段内。

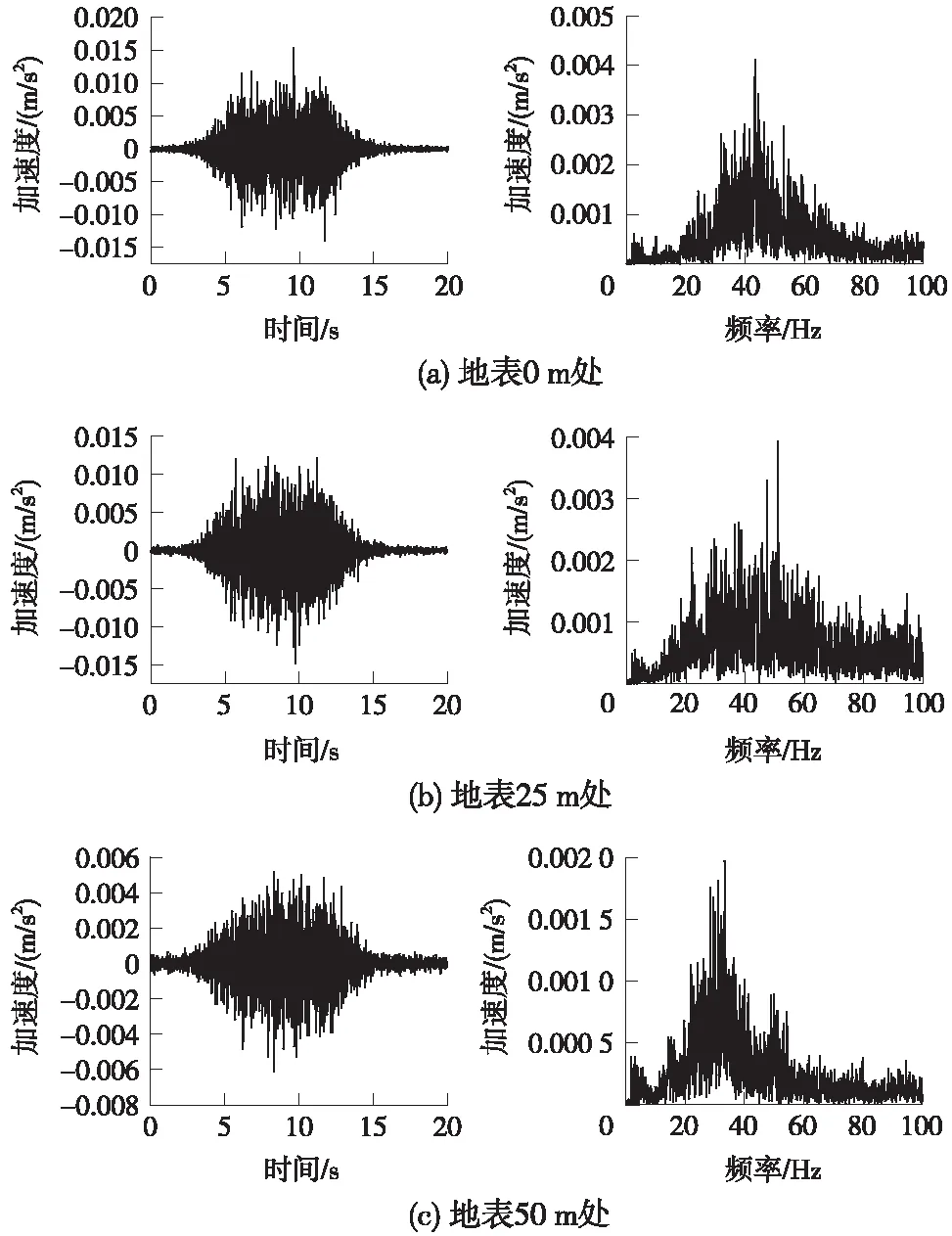
图6 地表典型位置处加速度时程及频谱

图7给出了地表不同位置拾振点的1/3倍频程谱。从图7可以看出：地铁列车在整体硫化压缩型扣件轨道上运行诱发的地表加速度响应主要集中在20～80 Hz频段，且地表各拾振点加速度响应1/3倍频程谱的峰值在中心频率40 Hz左右取得最大值，这也与上述地表响应频谱图表现出的规律相吻合；在1～1.6 Hz频段，由于这部分频率成分的地表振动主要源于列车准静态荷载的作用，因此，他们随着距离的增大有明显衰减，振动加速度级衰减可达24.6 dB；在1.6～6.3 Hz频段，地表振动响应随距离增大的变化并不明显，振动几乎无衰减；而在16～25 Hz频段及79～100 Hz频段，地表振动响应随距离增加呈现出先增大后衰减的规律，且相应加速度级分别在地表30 m及40 m处达到最大值；在其他频段，地表振动响应随距离增加在总体上呈现出振荡型式的衰减。此外，从图7中还可以发现，在40～100 Hz频段，地表振动响应在距隧道中线40 m范围内衰减较为缓慢，振动衰减量值极为有限，但从距隧道中线40 m地表到距隧道中线50 m地表，振动却有较大衰减，振动加速度级衰减量值最大可达12.3 dB。

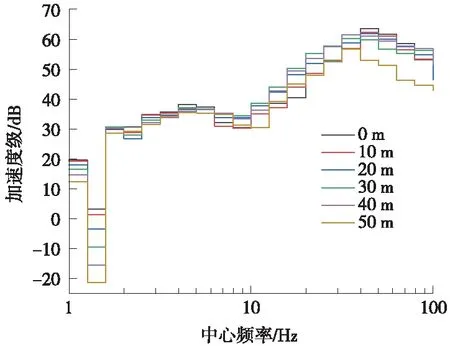
图7 地表不同拾振点1/3倍频谱

图8给出了采用整体硫化压缩型减振扣件时，地表最大Z振级随距离的变化情况。

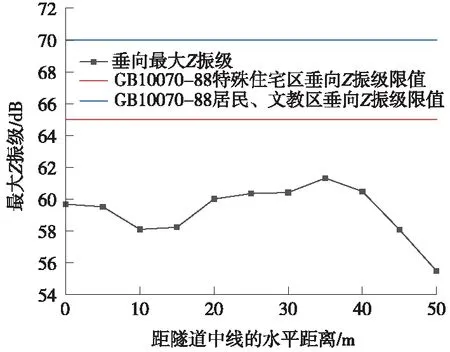
图8 地表各拾振点最大Z振级

从图8可以看出：在研究工况下，运行地铁列车诱发距加载隧道中线50 m范围内地表的最大Z振级量值在55.5～61.3 dB内；随着距离增加，地表最大Z振级总体呈衰减趋势，但在距加载隧道中线40 m范围内表现得不明显，在距加载隧道中线10 ～35 m内存在较为显著的放大区，地表最大Z振级在35 m处最大，量值达61.3 dB；使用整体硫化压缩型减振扣件后，在距离加载隧道中线大于40 m的地表范围，地表最大Z振级随着距加载隧道距离的增大有较为显著的衰减。需说明的是，对比GB 10070—1988《城市区域环境振动标准》，对城市不同区域最大Z振级限值的要求可知，使用整体硫化压缩型减振扣件能满足一般地铁区段的减振需求。

4 结论

针对我国自主研发的新型整体硫化压缩型减振扣件在无锡地铁中的应用效果问题，通过建立车轨动力耦合模型及轨道-隧道-地层耦合系统的2.5维数值模型，对其应用情况下列车运行引发的轨道、隧道及大地振动响应进行了研究，揭示了该种新型扣件的减振性能，明确了其应用时地铁环境振动的量值特征及传播特性。通过研究，得到以下结论。

(1)使用新型整体硫化压缩型减振扣件后，地铁列车运行引起的地表垂向加速度响应频谱峰值出现在30～50 Hz频段内。

(2)在采用新型整体硫化压缩型减振扣件的情况下，运行列车诱发的振动在从钢轨至道床传递过程中，各频段分频振级传递损失均在30 dB以上，且分频振级传递损失最大值可达54.6 dB，而最大Z振级的传递损失也可达34.4 dB。

(3)在地铁隧道埋深20 m且采用新型整体硫化压缩型减振扣件的情况下，运行地铁列车诱发距隧道中线50 m范围内地表的振动响应在总体上随距离增加而衰减，虽然衰减量值较为有限，但在该内，地表最大Z振级量值在55.5～61.3 dB内，均处于较小的量值水平。

(4)新型整体硫化压缩型减振扣件具有良好的减振性能，能满足一般地铁区段的减振需求，在地铁线路中具有良好的应用前景。