寿县不同强度雾的微物理特征及其与能见度的关系

张浩 石春娥 杨军 倪婷

1 安徽省气象科学研究所/大气科学与卫星遥感安徽省重点实验室，合肥 230031

2 寿县国家气候观象台/中国气象局淮河流域典型农田生态气象野外科学试验基地，安徽省寿县 232200

3 南京信息工程大学大气物理与大气环境重点实验室，南京 210044

1 引言

雾是大量微小水滴或冰晶浮游空中，使水平能见度低于1.0 km 的天气现象（中国气象局, 2007），其本质是及地的云。雾对社会经济的影响，主要表现在低能见度对陆、海、空交通运输的影响，随着我国交通运输业的快速发展，这种影响日益突出。根据“雾的预报等级”标准（GB/T 27964-2011）（中华人民共和国国家质量监督检验检疫总局和中国国家标准化管理委员会, 2012），雾可以分为大雾、浓雾、强浓雾、特强浓雾四个等级，其中，对交通运输业影响较大的是能见度低于200 m 的强浓雾和特强浓雾。如气象行业标准“公路交通高影响天气预警等级”（QX/T 414-2018）（中国气象局,2018）中规定，当预报未来2 h 内出现特强浓雾、6 h内出现强浓雾，气象部门将分别发布红色预警和橙色预警。因此，有必要研究不同强度雾的微物理特征及能见度影响因子，进一步提高强浓雾的预报、预警能力。

影响雾中大气能见度的两个主要因素是雾滴谱分布和含水量（Eldridge, 1961; Gerber, 1981; 鲍宝堂等, 1995; 李子华和吴君, 1995; Wendish et al.,1998; Ma et al., 2003; 刘端阳等, 2009; 岳岩裕等,2013; 张曦等, 2016; 王庆等, 2019）。大量的观测表明，受不同气候条件、生态环境的影响，不同地区、不同类型的雾，甚至雾的不同发展阶段，其微物理特征有明显的差异，能见度与微物理量的关系也不相同。 常见的雾滴谱分布有Junge 分布和Deirmendjian 分布，如李子华和吴君（1995）的研究发现重庆市冬季市区雾滴谱服从Junge 分布，市郊符合Deirmendjian 分布，从市郊向市区雾滴数密度愈来愈大，雾滴尺度和含水量愈来愈小；刘端阳等（2009）对发生在南京郊区的连续浓雾天气进行观测，分析发现，雾滴谱服从Deirmendjian 分布，谱型基本呈指数下降，雾滴主要集中在小滴段；王庆等（2019）分析发现济南一次冬季雾雾滴谱谱型呈“三峰”结构，雾中以小滴为主，直径8 μm 以下的小滴占总数的90%以上。Meyer et al.（1980）对一次辐射雾观测分析发现，在雾最浓的时候，雾滴谱出现多峰分布。

雾滴谱分布特征、含水量等微物理量是基于数值模式结果进行能见度参数化的重要参数。Koenig（1971）指出消光系数是雾滴谱分布和米散射消光系数的函数，Kunkel（1984）根据消光系数和含水量的关系，建立了能见度的参数化公式，并广泛应用于能见度的模拟计算（Benjamin et al.,2004; Gao et al., 2007）。Gultepe et al.（2006）研究表明能见度参数化方案中必须考虑雾滴数浓度，否则会增加能见度模拟的不确定性。国内学者分别基于广东茂名（黄辉军等, 2009）、山西（林艳等,2010）、湖北恩施（孟蕾等, 2010）、湖北荆州（荣昕, 2013）观测的雾含水量、雾滴数浓度、有效半径等微物理量，建立了适合本地的能见度参数化方案，取得较好的模拟效果。

淮河流域位于我国南北气候过渡带，水系纵横，河流、湖泊众多，每年秋冬季多雾、霾天气，如安徽沿淮淮北是安徽省三个雾高发区之一（Shi et al.,2008），多条高速公路贯穿该区域。安徽省2010年开始建设全网覆盖的高速公路自动能见度观测网络，根据2010 年9 月至2011 年12 月高速公路能见度资料，安徽高速公路强浓雾的高发路段主要位于安徽北部，由强浓雾造成的恶性交通事故时有发生。另外根据寿县国家气候观象台观测记录，2000～2018 年寿县年平均雾日数达36.7 d。因此，值得深入研究该地区雾的边界层、微物理特征，以及探讨辐射降温、平流和逆温等因子对雾过程的影响。2019 年1 月上中旬我们在寿县国家气候观象台开展了雾的外场观测试验，本文利用观测期间的雾滴谱资料，结合观象台常规观测资料，分析了不同强度雾的微物理特征，以及能见度与含水量、雾滴数浓度、相对湿度之间的关系，在此基础上建立能见度参数化方案，为该地区基于数值模式结果开展雾的预报、预警提供科学依据。

2 观测概况与研究方法

2.1 观测概况

观测场地位于寿县国家气候观象台内（32.43°N，116.78°E），海拔25.7 m，观测场下垫面平坦开阔，四周为农田。寿县国家气候观象台所在的淮河流域以辐射雾为主，主要发生在冬半年。2000～2018 年寿县年平均雾日数为36.7 d，其中1月最多，平均为4.8 d。2019 年1 月2～15 日，项目组在观象台进行了为期两周的雾综合观测，包括大气边界层特征、雾滴谱、常规气象要素等观测，其中1 月4、5、7 日、9～11 日出现降水，在雨后和降雨间歇期出现了不同强度的雾过程，为排除降水对观测数据的影响，本文选取1 月7 日20 时（北京时，下同）至8 日20 时、1 月11 日20 时至15 日06 时的观测数据进行分析。

雾滴谱的观测利用美国DMT 公司生产的FM-100 型雾滴谱仪（Eugster et al., 2006; 刘端阳等,2009），滴谱仪可以连续测量雾滴数量，采样频率为1 Hz，测量粒径范围为2～50 μm，分20 档。能见度（V）、相对湿度（RH）、气温（T）、风速（WV）等气象要素来自于寿县国家气候观象台的常规业务观测，数据时间间隔均为1 min。为便于比较，本文首先将雾滴谱数据进行1 min 平均。雾滴谱仪采样口距地面高度约1.2 m，雾滴谱仪与能见度仪等常规气象仪器之间水平距离约150 m。

2.2 分析方法

关于雾微物理特征的研究，以往大多将雾的生消过程划分为不同发展阶段进行比较分析（刘端阳等, 2009; 方春刚和郭学良, 2019; 王庆等, 2019），而阶段的划分并无统一标准，一般划分为形成阶段、发展阶段和成熟阶段，但各阶段与雾的强度并无明确的对应关系，不能得到不同强度雾微物理特征的差异。为探寻强浓雾与普通雾微物理特征及能见度影响因子的区别，本文参考国家标准“雾的预报等级”（中华人民共和国国家质量监督检验检疫总局和中国国家标准化管理委员会, 2012），根据能见度对雾过程进行分类，即将雾分为大雾(500 m≤V＜1000 m)、浓雾(200 m≤V＜500 m)、强浓雾（V＜200 m）三个等级。

众所周知，雾滴是在充足水汽的供应下，通过气溶胶粒子核化凝结而成。在雾的生消过程中，大气气溶胶粒子吸湿增长形成雾滴，雾滴的增加一方面通过对光的衰减直接导致能见度降低，另一方面小雾滴通过碰并增长，大雾滴数浓度不断增加，Eldridge（1971）指出大雾滴的增多对含水量增加起主要贡献作用。

式中，n是每一粒径范围内粒子数密度，Qext是半径为r的雾滴的Mie 消光系数；Qext与粒子半径和可见光的波长有关。当雾滴直径超过4 μm，Qext变为2。对于粒径小于4 μm，其值在3.8 至0.9 之间波动（Koenig, 1971; Brenguier et al., 2000）。

根据消光系数可计算能见度（Stoelinga and Warner, 1999）：

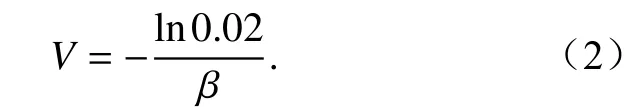
目前的数值预报业务中，一般的业务模式并没有雾滴谱的输出，因此，多采用Kunkel（1984）给出计算 β的经验公式：

式中，L是含水量（单位：g m-3）。可见消光系数与含水量存在指数关系，即含水量的增加，使消光作用增强，导致能见度降低。

很多学者在利用中尺度气象模式结果计算能见度时使用公式（2）、（3）（Gao et al., 2007）。然而Gultepe et al.（2006）指出，公式（3）会明显高估或低估能见度（不确定性超过50%），具体取决于环境条件。基于对大量外场观测资料的分析，Gultepe et al.（2009）得到基于含水量和雾滴数浓度计算能见度的公式：

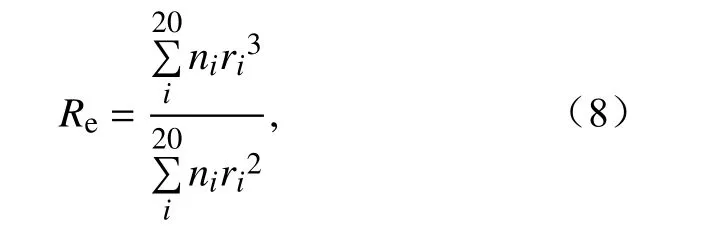
式中，ni为第i档雾滴数量；Sa为气流速度，约为13 m s-1；S为雾滴谱仪采样面积（S=0.24 mm2）；ρ为水的密度（约为1 g cm-3）；di（单位：μm）为第i档雾滴直径的上限值和下限值的平均；ri（单位：μm）为第i档雾滴半径的上限值和下限值的平均。

3 雾天气过程简况

式中，N是雾滴数浓度（单位：cm-3）。Gultepe et al.（2009）认为用该公式计算雾中能见度更加精确，但由于一般的气象模式并不直接输出雾滴数浓度，这阻碍了该公式的推广应用。

综上所述，影响雾中能见度的微物理量包括：含水量、数浓度和雾滴尺度。本文根据雾滴谱仪观测的每档雾滴数量计算出雾滴数浓度、含水量、平均直径（D，单位：μm）、有效半径（Re，单位：μm）等微物理量。具体计算公式如下：

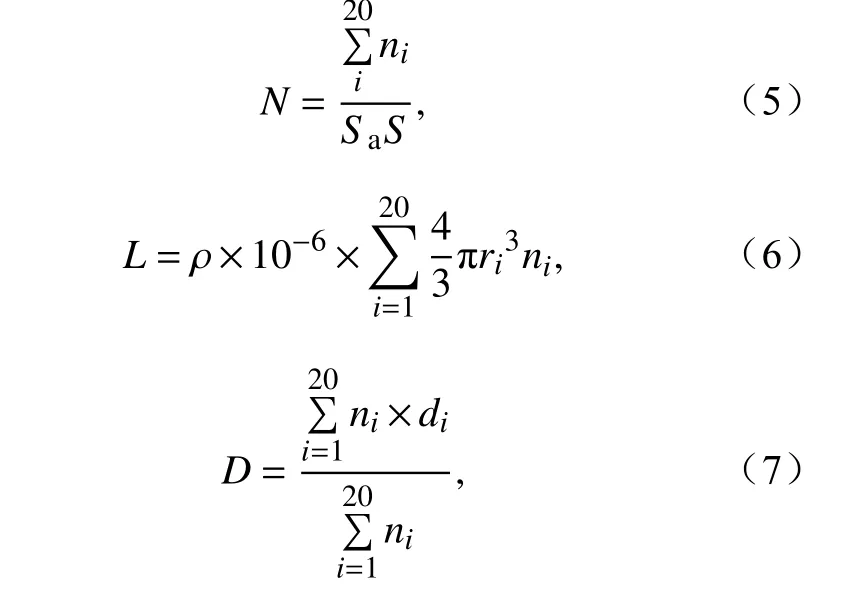
图1 为观测期间能见度、相对湿度等气象要素和雾微物理量随时间的变化。表1 给出了图1 中持续时间超过或接近1 h 的不同强度雾过程的起止时间。

由图1 可以看出，观测期间共出现4 次雾天气过程（包括强浓雾、浓雾、大雾），分别出现在1月7 日22:01 至8 日11:43、1 月12 日00:44 至12日08:42、1 月13 日01:48 至13 日11:15、1 月13日19:42 至14 日08:29，其中第2、3 次过程达到了强浓雾等级，两次强浓雾分别持续399 min、421 min（表1）。4 次雾过程都具有辐射雾的变化特征，入夜后，随着地面降温，能见度下降，雾形成，日出后随着地面升温，雾逐渐消散；第2、3次雾过程降温显著，如第二次雾过程中，气温从11 日20 时的2.9°C 降至12 日05 时的-2.9°C，降温幅度接近6°C，能见度也从3 km 左右降至100～200 m，雾逐渐形成并迅速变浓。同时可以看到在第2、3 次雾过程中，能见度短时间内迅速下降，如13 日01:48 第3 次雾刚形成时，能见度为996 m，到03:13 降至500 m，03:43 降至200 m 以下，到04:28，能见度下降至86 m，从大雾（500 m≤V＜1 km）到浓雾（200 m≤V＜500 m）经历了84 min，从浓雾到强浓雾（V＜200 m）仅用了30 min，体现了强浓雾的爆发性增长特征。

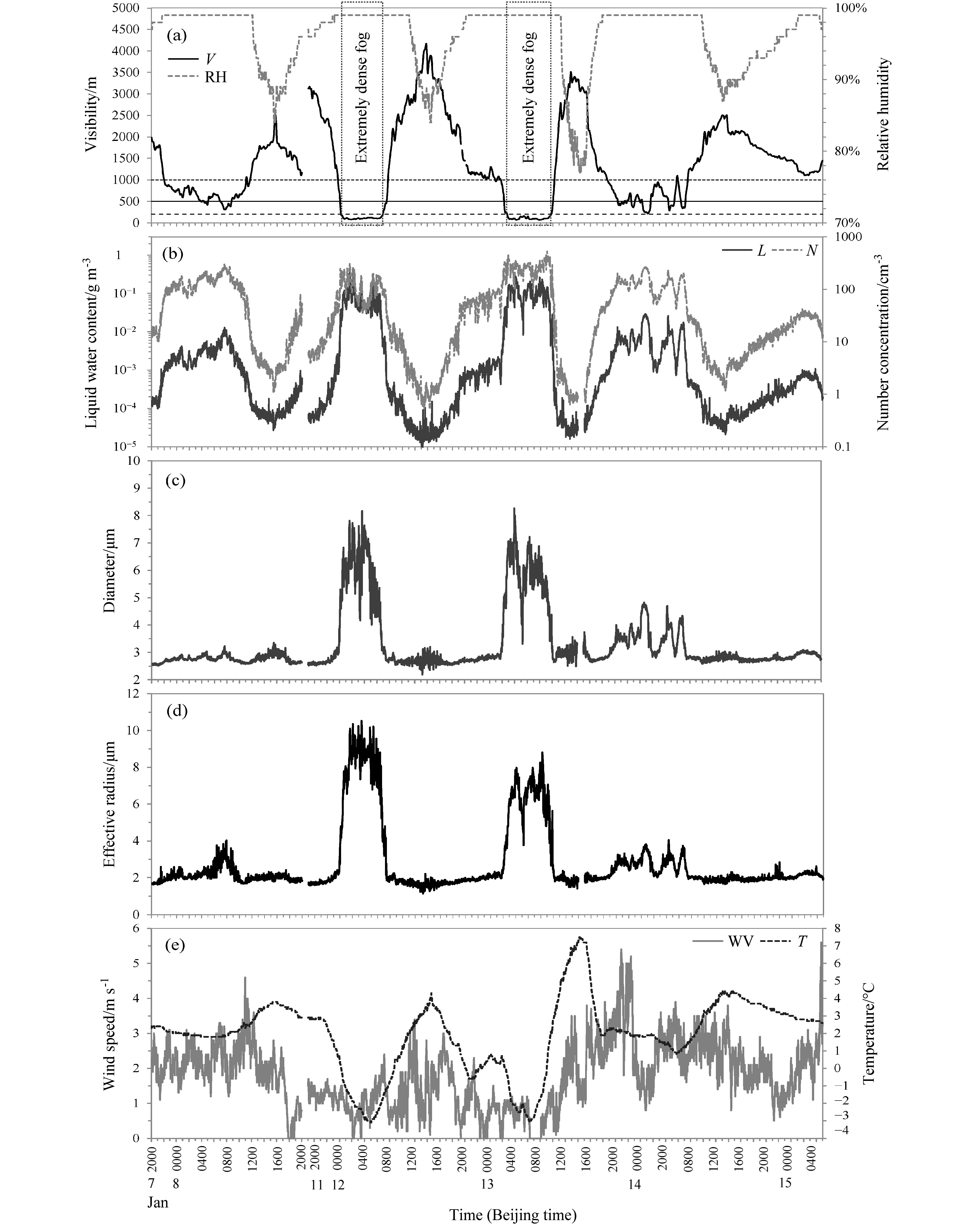
图1 2019 年1 月寿县雾综合观测期间（a）能见度（V）和相对湿度（RH）、（b）含水量（L）和数浓度（N）、（c）平均直径、（d）有效半径、（e）风速（WV）和气温（T）随时间的变化Fig. 1 Temporal variations of (a) visibility (V) and relative humidity (RH), (b) liquid water content (L) and number concentration (N), (c) mean diameter, (d) effective radius, (e) wind speed (WV) and temperature (T) in Shouxian County during fog comprehensive observation in January 2019

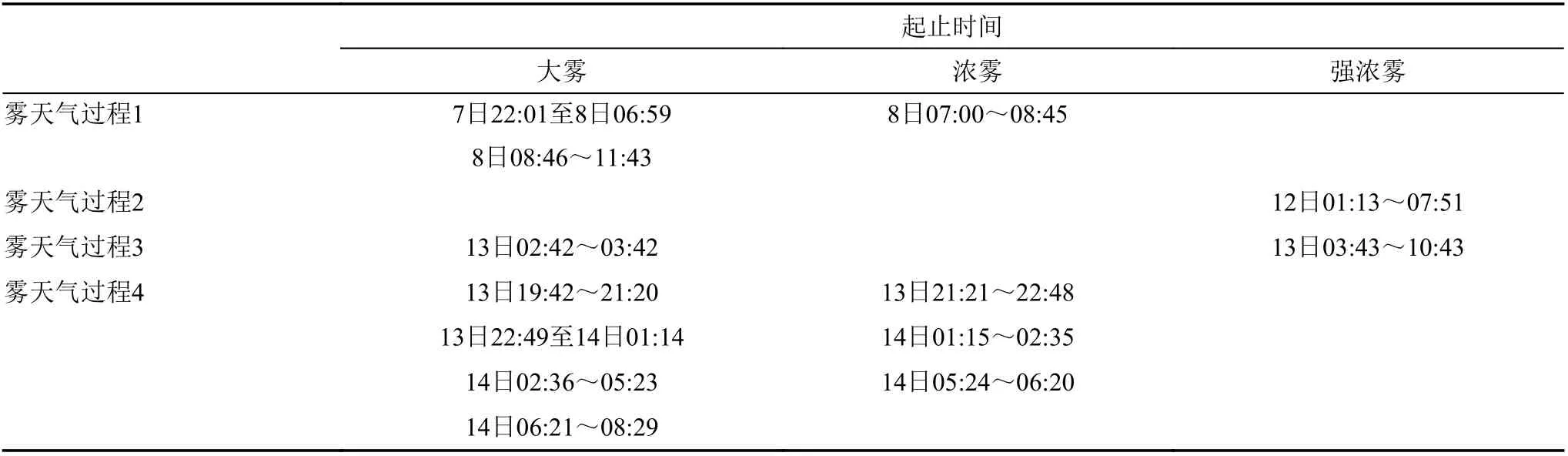
表1 2019 年1 月寿县雾综合观测期间不同强度雾过程起止时间Table 1 Start and end time of fog processes with different intensities in Shouxian County during fog comprehensive observation in January 2019

从能见度和相对湿度的变化可以看出，能见度与相对湿度呈反相关关系，雾过程期间，相对湿度记录最大值为99%，说明观测仪器存在系统误差。从风速变化来看，雾时平均风速都在3 m s-1以下，强浓雾时段风速最大只有2.1 m s-1。气温在雾过程期间明显偏低，雾天平均气温低于1.9°C，最高不超过2.5°C。含水量、数浓度、平均直径、有效半径等微物理量也有明显的变化，与能见度有很好的反对应关系，低能见度时各微物理量明显升高，其中在强浓雾过程中各微物理量基本达到峰值。

4 不同强度雾微物理结构特征

表2 给出了寿县不同强度雾微物理量的统计结果，也给出了南京、济南等地雾的观测分析结果。

（1）数浓度。寿县所有雾样本的数浓度平均值为153.7 cm-3，大雾、浓雾、强浓雾的平均数浓度分别为113.2 cm-3、189.3 cm-3、195.6 cm-3，随着雾强度增强，雾滴数浓度增大，从大雾到浓雾，雾滴数浓度增加显著，平均值增加76.1 cm-3（增幅67%），而从浓雾到强浓雾，数浓度增幅不大，仅增加6.3 cm-3（增幅3%）。

（2）含水量。寿县所有雾样本的含水量平均值为0.036 g m-3，不同强度雾含水量差异显著，从大雾、浓雾到强浓雾，含水量增大，大雾、浓雾和强浓雾阶段含水量平均值分别为0.003 g m-3、0.01 g m-3和0.09 g m-3，强浓雾阶段的最大含水量为0.38 g m-3。

（3）平均直径。整个雾过程的平均直径为4.11 μm，随着雾的强度增强，平均直径增大，大雾、浓雾、强浓雾的雾滴平均直径分别为2.97 μm、3.62 μm 和5.88 μm，从浓雾到强浓雾，雾滴平均直径增加2.26 μm（增幅62%）。

（4）最大直径。雾滴最大直径可达到48.5 μm，不同于平均直径，强浓雾阶段的最大直径和峰值直径都不及浓雾阶段大，但比较接近，明显大于大雾阶段，说明浓雾过程中大雾滴维持时间较长，可能强浓雾阶段大雾滴沉降较快。

由图1 和表2 都可以看出，不同强度雾，其微物理量都存在较大起伏。如从各物理量的最大值和最小值的比值看，数浓度和平均直径都是强浓雾阶段的变化幅度最大，含水量是大雾阶段变化幅度最大，浓雾阶段的变化幅度都是居中或最小。从比值的大小看，含水量的变化幅度最大（即最大值与最小值的比值最大）。如果从强浓雾微物理量最大值与最小值的比值看，寿县强浓雾与南京雾（刘端阳等, 2009）的成熟阶段最接近，这可能与南京雾划分的成熟阶段对应强浓雾有关。为进一步了解不同强度雾过程中含水量的起伏程度及样本集中程度，分别计算了大雾、浓雾和强浓雾阶段含水量的变异系数（标准差/平均值），以及平均值±1 倍标准差的样本数占总样本的比例（表3）。由表可见，大雾阶段含水量的变异系数和平均值±1 倍标准差的样本数占总样本的比例大于浓雾、强浓雾阶段，浓雾和强浓雾阶段差别不大，可见大雾阶段含水量的起伏更大。

表2 2019 年1 月寿县雾综合观测期间雾微物理特征及与其他地区的比较Table 2 Comparisons of microphysical characteristics of fog in Shouxian County during fog comprehensive observation in January 2019 and other areas

表3 2019 年1 月寿县雾综合观测期间不同强度雾阶段含水量的变异系数、平均值±1 倍标准差的样本数占总样本的比例Table 3 Variation coefficients and proportion of sample number (within mean ± one times standard deviation) to the total sample number for liquid water content in different fog intensity stages in Shouxian County during fog comprehensive observation in January 2019

综上所述，随着雾的强度增强，能见度降低，雾中含水量显著增大，雾滴数浓度、平均直径增大；从大雾到浓雾，雾滴数浓度显著增大（增幅67%），而从浓雾到强浓雾，雾滴数浓度变化不大，但雾滴直径明显增大（增幅62%）。表2 中列出了近年来中国不同地区的观测结果，可以得到同样的结论，即从雾的形成阶段到成熟阶段，雾滴数浓度和含水量显著增大。

为进一步比较不同强度雾的微物理特征，图2用箱线图给出了大雾（Fog）、浓雾（Dense fog）、强浓雾（Extremely dense fog，简写为ExDense fog）阶段的雾滴数浓度、含水量、有效半径的统计结果。统计量包括平均值，中位值，一、三四分位值，最大值，最小值。由图2 可见，雾滴数浓度和有效半径的中位值与均值基本上都位于长方形的中间位置，说明这两个参量接近正态分布，而浓雾阶段含水量的均值明显偏向大值一侧，说明浓雾阶段少量大雾滴对含水量的贡献较大。根据一、三四分位的位置，可以看出含水量、有效半径在强浓雾阶段的第一四分位高于浓雾阶段的第三四分位，浓雾阶段的第一四分位高于大雾阶段的第三四分位，但从数浓度来看，强浓雾与浓雾和大雾的变化范围均有所重合，差异不明显。如果以75%的样本（或者一、三四分位）能区分为接受标准，大雾、浓雾、强浓雾的含水量、有效半径存在显著差异，如强浓雾的含水量有75%以上的样本大于0.049 g m-3，浓雾的含水量有75%以上的样本小于0.011 g m-3，大雾的含水量有75%以上的样本小于0.004 g m-3，即如果含水量大于0.049 g m-3，则有75%的可能性会出现强浓雾。若将比例提高至95%，对于强浓雾，含水量下限为0.023 g m-3。因此，在基于数值模式结果进行强浓雾预报、预警时，可以将0.02 g m-3作为判别该地区强浓雾的含水量阈值。

图2 2019 年1 月寿县雾综合观测期间大雾（Fog）、浓雾（Dense fog）、强浓雾（ExDense fog）阶段（a）雾滴数浓度、（b）含水量、（c）有效半径（Re）分布箱线图。上下两个横线分别表示最大值和最小值；长方形中的横线表示中值，实心圆表示均值；长方形的下、上边分别表示第一、三四分位值Fig. 2 Box plots of the (a) droplet number concentration, (b) liquid water content, and (c) effective radius (Re) for fog, dense fog, extremely dense fog(ExDense fog) in Shouxian County during fog comprehensive observation in January 2019. The upper transverse line: maximum, the lower transverse line: minimum; transverse line within the rectangles: median; solid circle within the rectangles: mean; the upper and lower borders of the rectangles:25th and 75th percentiles

图2c 给出了有效半径的统计特征，雾滴有效半径是表征云雾光学特性的重要参数，已有研究表明，雾滴有效半径与含水量/数浓度呈正相关关系（Gultepe et al., 1996; Reid et al., 1999; 岳岩裕等,2013）。从图2c 中可以看出，强浓雾有效半径的平均值为7.3 μm，最大值为10.5 μm，有75%以上的样本大于6.4 μm；而大雾、浓雾有效半径远远低于强浓雾，平均值分别为2.3 μm、3.1 μm，最大值不超过4 μm。进一步统计发现，强浓雾有效半径有超过95%的比例大于4.7 μm。

5 不同强度雾滴谱分布特征

图3a 为不同强度雾的雾滴数浓度谱分布特征，图中点线为实测的谱分布，实线和短划线为由拟合公式计算的谱分布。可以看出，强浓雾、浓雾、大雾数浓度谱分布均为双峰结构，强浓雾最大峰值出现在3 μm 处，另一个峰值在13 μm 处，浓雾、大雾最大峰值分别出现在3 μm、2 μm 处，另一个峰值均在21.5 μm 处；数浓度谱分布整体偏向小粒子一端，直径9 μm 以下（包括9 μm）的粒子数占总粒子数的比例，强浓雾阶段为82.6%，浓雾、大雾阶段超过90%。在数浓度上，强浓雾平均雾滴数浓度大于浓雾和大雾，特别是在10～30 μm 之间差别比较大。而在40 μm 以上，强浓雾阶段的雾滴数反而减少，这反映了雾滴吸湿增长和重力沉降的影响。

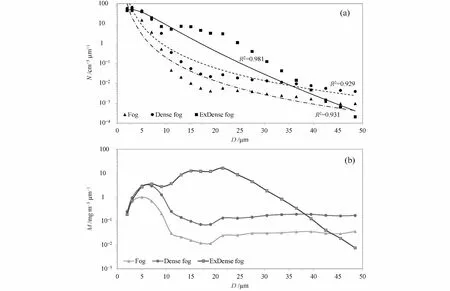
图3 2019 年1 月寿县雾综合观测期间不同强度雾雾滴（a）数浓度谱、（b）雾水质量浓度谱分布Fig. 3 Distributions of (a) the droplet number concentration spectrum and (b) liquid water mass concentration spectrum for different fog intensities in Shouxian County during fog comprehensive observation in January 2019

从分布的谱型来看，强浓雾、浓雾、大雾数浓度谱分布均呈指数递减，其中强浓雾的平均雾滴谱符合Deirmendjian 分布：N(D)=66090.49D4.929exp(-8.125D0.398)，与南京（刘端阳等, 2009）、济南（王庆等, 2019）和重庆沙坪坝（李子华和吴君,1995）的雾滴谱分布特征类似；而浓雾和大雾的雾滴谱符合Junge 分布，拟合公式分别为N(D)=2692.9D-3.584、N(D)= 1452.6D-3.875，与重庆陈家坪（李子华和吴君, 1995）和茂名（黄辉军等, 2009）、湛江（张舒婷等, 2013）、厦门（张曦等, 2016）的海雾谱分布特征类似。另外可以看出，拟合谱分布曲线和实测谱分布曲线比较一致，决定系数R2均在0.92 以上，说明谱分布函数能够反映雾的微物理结构特征。

图3b 为不同强度雾的雾水质量浓度谱分布特征，可以看出，强浓雾的雾水质量浓度明显大于浓雾和大雾，强浓雾质量浓度谱呈现多峰特征，最大峰值出现在21.5 μm 处，另两个峰值分别在15 μm、7 μm 处，13～27.5 μm 的雾滴对含水量的贡献较大；浓雾雾水质量浓度谱呈现双峰特征，峰值分别出现在5 μm、21.5 μm 处；大雾雾水质量浓度谱的峰值在5 μm 处，之后没有形成峰值，浓雾、大雾基本都是3～9 μm 的雾滴对含水量的贡献较大。

6 能见度参数化方案

雾对大气能见度的影响与雾微物理量密切相关，含水量、数浓度是影响能见度的重要因子。另外，相对湿度也对大气能见度有显著影响（张浩等,2017; 侯梦玲等, 2017）。本节利用选取时段的综合观测资料，首先分析能见度与含水量、数浓度、相对湿度的关系，然后从原始序列中每隔2 组数据选取一组作为验证样本，其他数据作为建模样本，分别建立基于含水量、数浓度、含水量×数浓度、相对湿度的能见度参数化方案，并对不同能见度参数化方案进行评估检验。

6.1 能见度与含水量、数浓度、相对湿度的关系

根据图1 雾微物理量的时间变化，可以看到含水量与数浓度变化趋势基本一致，进一步统计分析二者的相关关系（图4），可以看出，总体上含水量随着数浓度的增加而增加，当数浓度在50 cm-3以下，含水量随数浓度的增加而迅速增加，但当数浓度大于50 cm-3时，含水量差异比较大，对于一个给定的数浓度，含水量相差1～2 个数量级；同样，含水量一定时，雾滴数浓度变化范围可以从几十 cm-3到几百cm-3。因此，本文在建立能见度参数化方案时，不仅建立了能见度与含水量、雾滴数浓度的单参数化方案，还尝试建立了能见度与含水量×数浓度的双参数化方案，并进行比较。

图4 2019 年1 月寿县雾综合观测期间雾含水量与雾滴数浓度散点图Fig. 4 Scatter plot between the liquid water content and number concentration of fog droplets in Shouxian County during fog comprehensive observation in January 2019

图5 分别给出能见度与含水量（V-L）、数浓度（V-N）、含水量×数浓度（V-L×N）、相对湿度（V-RH）的变化关系。可以看出，含水量与能见度呈显著的反相关关系，二者的相关系数达到0.965，随着含水量增加，能见度逐渐下降，当含水量大于0.02 g m-3时，能见度基本在200 m 以下，即达到强浓雾；数浓度与能见度同样呈显著的反相关关系，但变化关系没有含水量与能见度那么密切，如图5b 中的点比较分散，相关系数为0.822，当雾滴数浓度低于50 cm-3时，能见度随着数浓度增加迅速下降，而当数浓度大于50 cm-3时，能见度变化比较缓慢，对于同样的数浓度，能见度变化范围比较大，如数浓度在100 cm-3附近，能见度变化从几十米到近1 千米。由于能见度随着含水量、数浓度增加均呈减小趋势，因此分析了能见度与（L×N）-1的关系，二者相关系数达到了0.927，高于能见度与雾滴数浓度的相关性，但低于能见度与含水量之间的相关性。从相对湿度与能见度的变化关系来看，二者呈对数关系，相关系数为0.724，明显低于能见度与含水量、雾滴数浓度间的相关性，能见度随着相对湿度增加而减小，但变化趋势比较缓慢，对于同样的相对湿度，能见度变化范围比较大，高相对湿度更加明显，如当相对湿度为99%（可以认为饱和）时，能见度变化范围为68～3666 m，可见，相对湿度不能作为雾的判断依据，尤其不能作为强浓雾的判断依据。

图5 2019 年1 月寿县雾综合观测期间（a）含水量、（b）数浓度、（c）含水量×数浓度、（d）相对湿度与能见度的关系Fig. 5 Relationships between (a) liquid water content, (b) number concentration, (c) liquid water content×number concentration, (d) relative humidity and the visibility in Shouxian County during fog comprehensive observation in January 2019

能见度与（L×N）-1的相关系数略低于其与L的相关系数，这与Gultepe et al.（2006）的结论不同，Gultepe et al.（2006）认为要提高模式预报能见度的精准程度，必须考虑把数浓度用作一个独立变量，也即认为用V-L×N关系计算能见度更可靠。然而，从Gultepe et al.（2006）的分析中，我们并没有找到作者认为的V-L×N关系优于V-L关系的依据，比如作者在拟合V-L×N与V-L关系时得到的均方根误差（RMSE）和平均相对误差（MRE）都相同（没有给出相关系数）。之后，Gultepe et al.（2009）利用一次海雾个例的秒级数据得到V-L×N相关系数远高于V-L、V-N的相关系数，并指出海雾与陆地雾的微物理特征存在显著差异，因此，需要分开建立参数化方案。而本文利用的是1 min 平均数据对陆地雾的分析，这可能是本文结果与Gultepe et al.（2009）结果不同的原因之一。为进一步分析能见度与含水量的相关性优于能见度与含水量乘以数浓度相关性的原因，首先根据图5a、b 的拟合关系，基于L、N分别得到每一个样本的计算能见度（Vcal），进一步得到观测能见度（Vobs）与计算能见度差值绝对值（|Vcal－Vobs|）的标准差，然后统计|Vcal－Vobs|在1 倍标准差范围内的样本数占总样本的比例。结果表明，基于N的拟合关系，（|Vcal－Vobs|）的标准差为0.405 km，有61.9%的样本在1 倍标准差范围内；而基于L的拟合关系，（|Vcal－Vobs|）的标准差为0.252 km，有64.4%的样本在1 倍标准差范围内。说明图5b中V-N数据的离散程度更高，因此将雾滴数浓度与含水量一起作为因子对能见度进行参数化，增加了样本的离散程度，导致相关系数变差。

6.2 能见度参数化方案建立及评估

从图4、图5b 可以看到，有相当一部分样本偏离最佳拟合线较远，如图4 的上半部、图5b 的下半部，这部分样本对应着较大的含水量（基本都大于0.02 g m-3）、能见度较低（低于150 m），属于强浓雾。另外，图5b、c 中，最佳拟合线底端，能见度150 m 以下的样本与总体样本之间存在明显的间隙，即能见度150 m 与300 m 之间样本稀疏。从图5a-c 可以看到当能见度低于200 m，能见度随上述物理量之间的变化比较平稳，基本呈直线。因此，我们对建模样本以能见度200 m 为界进行分段，分别建立能见度与含水量（L）、数浓度（N）、含水量×数浓度（L×N）之间的拟合方程，结果见表4。

表4 2019 年1 月寿县雾综合观测期间能见度与不同微物理量之间的拟合关系式Table 4 Fitting relationships between visibility and different fog microphysical parameters in Shouxian County during fog comprehensive observation in January 2019

利用四种能见度参数化方案对验证样本进行评估检验，检验方式有两种，一种是用所有建模样本建立的拟合方程，另一种是用分段建立的拟合方程，其中当能见度低于200 m 时（强浓雾），根据上述确定的含水量阈值为0.02 g m-3，因此，当含水量大于0.02 g m-3时，用V＜200 m 的拟合方程，反之用V≥200 m 的拟合方程。各种方案的验证检验结果见表5，从相关系数、平均相对误差、均方根误差来看，各个方案均是分段拟合的验证效果明显优于所有样本的拟合方式，除方案4 外，其他方案分段拟合的相关系数均在0.93 以上。如果不分段，方案1 明显优于其他方案，分段处理后，方案1、方案3 拟合的相关系数、平均相对误差和均方根误差都比较接近。可见，方案1、方案3 分段拟合效果比较好。尽管方案1、方案3 分段后的效果比较接近，但仍然是V-L关系略优于V-L×N关系，根据前面的分析，将雾滴数浓度与含水量一起作为因子对能见度进行参数化时增加了样本的离散程度，导致能见度拟合效果较单独考虑含水量的略差。

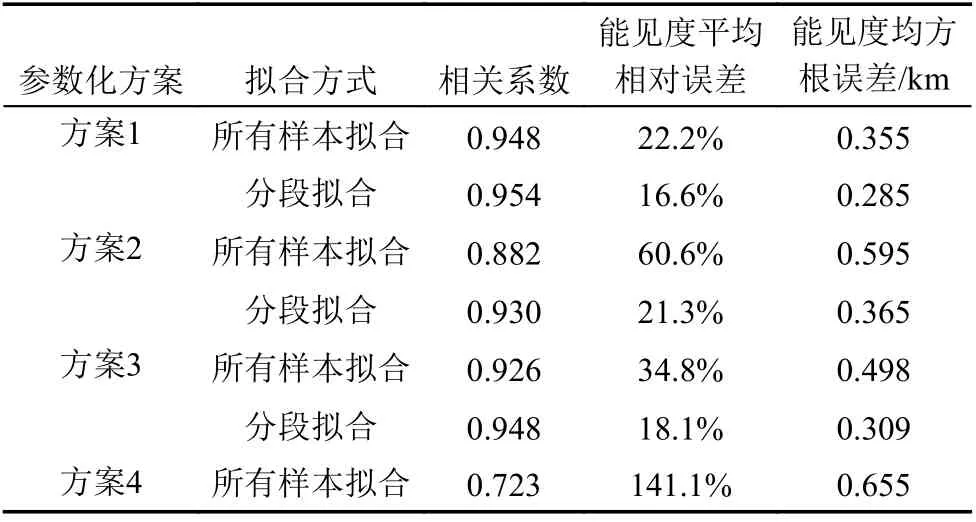
表5 2019 年1 月寿县雾综合观测期间不同能见度参数化方案验证结果Table 5 Verification results of different visibility parameterization schemes in Shouxian County during fog comprehensive observation in January 2019

图6 给出了前3 种方案分段拟合的能见度与观测能见度的对比。第一种、第三种能见度参数化方案拟合的能见度与观测能见度的变化趋势基本一致，并能很好地拟合出低能见度，第二种方案虽然能够拟合出与观测能见度比较一致的变化趋势，但存在高值高估现象。

图6 2019 年1 月寿县雾综合观测期间不同参数化方案拟合能见度与观测能见度对比Fig. 6 Comparison between fitting visibilities by different parameterization schemes and observed visibility in Shouxian County during fog comprehensive observation in January 2019

为进一步比较各方案对不同能见度范围的估算能力，对1 km 以下的能见度进行分级检验：按照0.5 km≤V＜1 km、0.2 km≤V＜0.5 km、V＜0.2 km三个等级，针对不同等级，分别进行TS 评分（Threat score,ST）、空报率（False alarm ratio,RFA）、漏报率（Missing rate,RM）和预报偏差（Frequency bias index,IFB）检验。

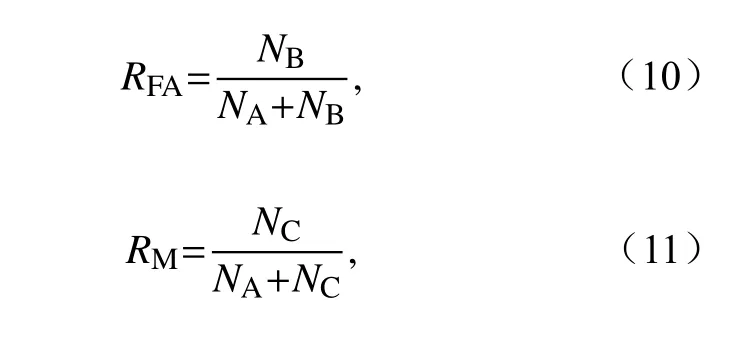
式中，NA为预报等级与实况等级相同的样本数（正确预报），NB为预报出现在等级内而实况未出现的样本数（空报），NC为预报没出现在等级内而实况出现的样本数（漏报）。从各统计量的定义可以看出，ST的范围是0（最差）～1（最好），越大越好；RFA和RM的取值范围是0（最好）～1（最差），越小越好；IFB的最佳取值是1，当IFB大于1，说明空报比例大于漏报比例，反之漏报比例更大。

表6 给出了前3 种方案分段拟合的不同等级能见度的评估检验结果，可以看出，对于大雾（0.5 km≤V＜1 km），方案1 在TS 评分、空报率、预报偏差方面都好于其他方案，漏报率不足0.2；对于浓雾（0.2 km≤V＜0.5 km），方案1 无论从TS 评分、漏报率、预报偏差方面都是最优的，空报率也比较低；对强浓雾（V＜0.2 km），各方案中各项检验指标结果一致，且TS 评分都达到0.875，空报率、漏报率都不足0.1，说明各个方案基本上均能准确的模拟出0.2 km 以下的低能见度。

表6 2019 年1 月寿县雾综合观测期间不同等级能见度评估检验结果Table 6 Evaluation and inspection results of visibility at different levels in Shouxian County during fog comprehensive observation in January 2019

综合来看，方案1 即基于含水量的分段能见度参数化方案，对能见度的估算效果最好，对1 km以下的低能见度具有更好的拟合效果。

7 结论与讨论

2019 年1 月上中旬在寿县国家气候观象台开展了雾的外场观测试验，通过观测资料分析了不同强度雾的微物理特征，以及能见度与含水量、雾滴数浓度、相对湿度之间的关系，在此基础上建立能见度参数化方案，并进行检验评估。

（1）随着雾的强度增强，雾中含水量显著增大，大雾、浓雾和强浓雾阶段含水量平均值分别为0.003 g m-3、0.01 g m-3和0.09 g m-3；当含水量大于0.02 g m-3，出现强浓雾的比例高达95%，强浓雾的含水量下限可定为0.02 g m-3。

（2）随着雾的强度增强，雾滴数浓度、雾滴尺度增加，从大雾到浓雾，雾滴数浓度显著增加（增幅67%），而从浓雾到强浓雾，雾滴尺度显著增大，平均直径、平均有效半径分别增加62%、135%；当雾滴有效半径大于4.7 μm，出现强浓雾的比例高达95%。

（3）强浓雾、浓雾、大雾雾滴数浓度谱分布均为双峰结构，谱分布整体偏向小粒子一端，谱分布均呈指数递减，但强浓雾谱型为Deirmendjian 分布，浓雾、大雾均为Junge 分布；强浓雾的雾水质量浓度明显大于浓雾和大雾，质量浓度谱呈现多峰特征，最大峰值出现在21.5 μm 处，13～27.5 μm的雾滴对含水量的贡献较大；浓雾雾水质量浓度谱为双峰分布，大雾为单峰型，最大峰值均出现在5 μm 处。

（4）含水量、数浓度与能见度均呈反相关关系，含水量对能见度的影响最为显著；分别采用全样本和分段方式建立了四种能见度参数化方案，其中基于微物理量的参数化方案更能反映实测能见度的变化趋势；评估检验结果表明，基于含水量的能见度分段拟合方案对能见度的估算效果最好，对1 km以下的低能见度具有更好的拟合效果。

尽管寿县地区雾的微物理特征与其他地区略有差异，但变化规律基本一致，即随着雾强度增强，能见度降低，雾中含水量显著增大，雾滴数浓度和雾滴直径增大。通过外场观测得到的寿县地区强浓雾微物理量诊断阈值，以及建立的能见度参数化方案，可望为东部地区强浓雾监测与预报提供科学支撑。