Hybrid Nanofluid Flow with Homogeneous-Heterogeneous Reactions

Iskandar Waini,Anuar Ishakand Ioan Pop

1Fakulti Teknologi Kejuruteraan Mekanikal dan Pembuatan,Universiti Teknikal Malaysia Melaka,Hang Tuah Jaya,76100,Durian Tunggal,Melaka,Malaysia

2Department of Mathematical Sciences,Faculty of Science and Technology,Universiti Kebangsaan Malaysia,43600,UKM Bangi,Selangor,Malaysia

3Department of Mathematics,Babe¸s-Bolyai University,400084,Cluj-Napoca,Romania

Abstract:This study examines the stagnation point flow over a stretching/shrinking sheet in a hybrid nanofluid with homogeneous-heterogeneous reactions.The hybrid nanofluid consists of copper(Cu)and alumina(Al2O3)nanoparticles which are added into water to form Cu-Al2O3/water hybrid nanofluid.The similarity equations are obtained using a similarity transformation.Then,the function bvp4c in MATLAB is utilised to obtain the numerical results.The dual solutions are found for limited values of the stretching/shrinking parameter.Also,the turning point arises in the shrinking region (λ＜0).Besides,the presence of hybrid nanoparticles enhances the heat transfer rate,skin friction coefficient,and the concentration gradient.In addition,the concentration gradient is intensified with the heterogeneous reaction but the effect is opposite for the homogeneous reaction.Furthermore,the velocity and the concentration increase,whereas the temperature decreases for higher compositions of hybrid nanoparticles.Moreover,the concentration decreases for larger values of homogeneous and heterogeneous reactions.It is consistent with the fact that higher reaction rate cause a reduction in the rate of diffusion.However,the velocity and the temperature are not affected by these parameters.From these observations,it can be concluded that the effect of the homogeneous and heterogeneous reactions is dominant on the concentration profiles.Two solutions are obtained for a single value of parameter.The temporal stability analysis shows that only one of these solutions is stable and thus physically reliable over time.

Keywords:Homogeneous-heterogeneous reactions;stagnation point;hybrid nanofluid;shrinking sheet;dual solutions;stability analysis

1 Introduction

Boundary layer flow produced by the stretching or shrinking surface was introduced by researchers many years ago.The pioneered work of the problems can be found in the literature[1-4].On the other hand,Hiemenz [5]was the first researcher to consider the boundary layer flow of a stagnation point over a rigid surface.Then,Homann [6]extended the problem to the axisymmetric flow,while Wang [7]considered the flow on a shrinking sheet.Furthermore,homogeneous (bulk) and heterogeneous (surface) reactions on the stagnation point flow were examined by Chaudhary and Merkin [8,9].A simple of these reactions with equal and different diffusivities for autocatalyst and reactant was introduced in their studies.Then,Merkin [10]extended the problem to the Blasius flow.The homogeneous and heterogeneous reactions have significant applications in the biochemical,catalysis,and combustion systems.Inspired by these studies,Khan and Pop [11]examined these effects on the flow towards a permeable surface.They noticed that dual solutions exist in the injection region but a unique solution is observed in the suction region.Besides,Kameswaran et al.[12]studied a similar problem by considering the magnetic field effects.They discovered that the skin friction coefficient and the concentration gradient increased with increasing of the magnetic parameter.Apart from that,several studies [13-15]involving homogeneous and heterogeneous reactions have been reported in the literature.

In 1995,Choi and Eastman [16]introduced nanofluid,which is a mixture of the base fluid and a single type of nanoparticles,to enhance the thermal conductivity.Some works on such fluids can be found in [17-23].Recently,some studies found that advanced nanofluid which consists of another type of nanoparticles and the regular nanofluid could improve its thermal properties,and this mixture is termed as ‘hybrid nanofluid’.The prior experimental works using the hybrid nanoparticles have been done by several researchers [24-26].Besides,the numerical studies on the flow of hybrid nanofluids were studied by Takabi and Salehi [27].Moreover,the dual solutions of the hybrid nanofluid flow were examined by Waini et al.[28-30].Other physical aspects were considered by several authors [31-38].Also,the review papers can be found in [39-44].

Motivated by the above mentioned studies,this paper considers the homogeneousheterogeneous reactions on hybrid nanofluid flow with Al2O3-Cu hybrid nanoparticles.Different from the work reported by Ramesh et al.[33],the present study considers the stagnation point flow towards a stretching/shrinking sheet.Most importantly,in this study,two solutions are discovered for a single value of parameter,and the stability of these solutions over time is tested.

2 Mathematical Model

The stagnation point flow triggered by a stretching/shrinking sheet in Al2O3-Cu/water hybrid nanofluid is considered.In Fig.1,the free stream and the surface velocities are given asue(x)=cxanduw(x)=dx,respectively,withc＞0,whereasd＜0 andd＞0 indicate the shrinking and stretching sheets,respectively,andd=0 indicates the static sheet.Meanwhile,the ambient and the surface temperatures are given byT∞andTw,respectively,and both are constants.The homogeneous-heterogeneous reactions are also taking into consideration.

Following Chaudhary and Merkin [8]and Merkin [10],a simple homogeneous reaction and the first order of heterogeneous reaction can respectively be written as

where these processes are assumed to be isothermal.Here,aandbare the chemical concentrations for speciesAandB,respectively,with the rate constantsk1andks.Thus,the equations that govern the hybrid nanofluid flow are [8,33]:

subject to:

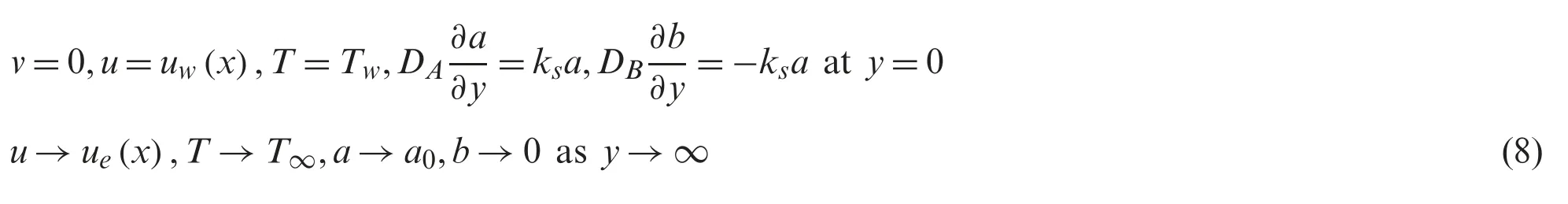
where the coordinates(x,y)with corresponding velocities(u,v)are measured along thex-andy-axes,andTrepresents the temperature.Besides,DAandDBare the corresponding diffusion coefficients of speciesAandB,anda0＞0.Further,the thermophysical properties can be referred to in Tabs.1 and 2.Note thatφ1(Al2O3) andφ2(Cu) are the nanoparticles volume fractions whereφhnf=φ1+φ2,and the subscriptsn1 andn2 correspond to their solid components,while the subscriptshnfandfsignify the hybrid nanofluid and the base fluid,respectively.

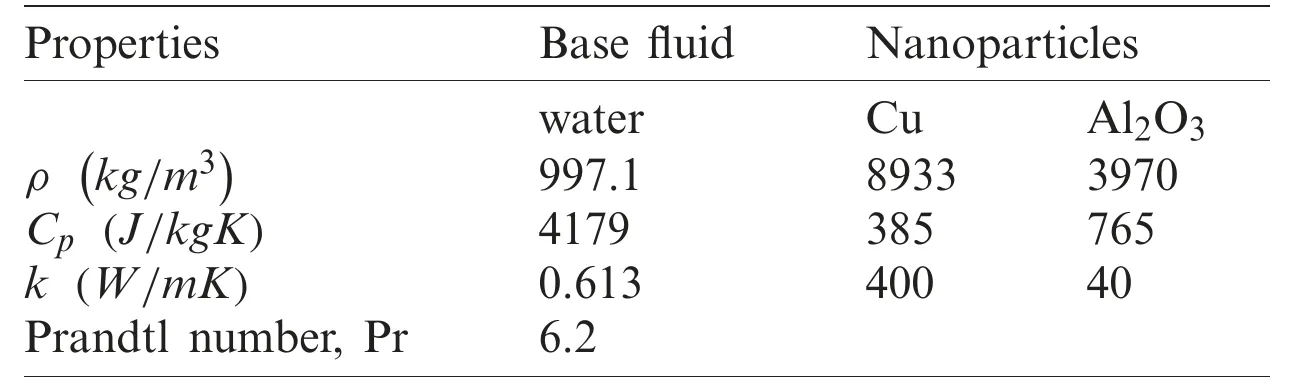
Table 1:Thermophysical properties of nanoparticles and water [19]

Table 2:Thermophysical properties of hybrid nanofluid [27]

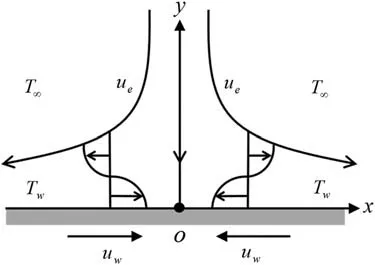
Figure 1:Flow configuration model

To obtain similarity solution,the following variables are employed [33]:

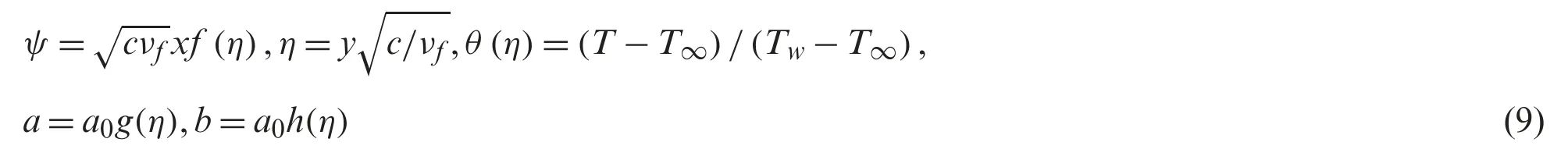
whereψis the stream function defined asu=∂ψ/∂yandv=－∂ψ/∂x.Then one obtains

It is noted that the continuity Eq.(3) is identically satisfied.

Now,Eqs.(4) to (7) respectively reduce to:

subject to:

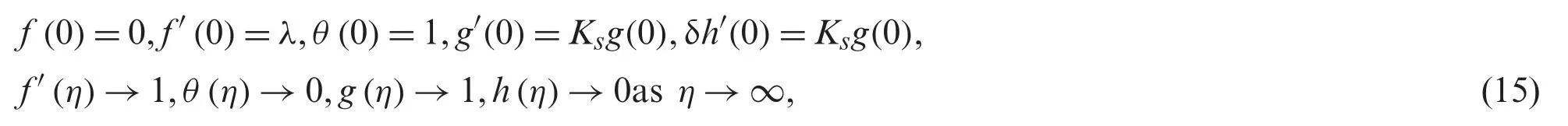
where primes denote the differentiation with respect toη.The physical parameters appear in Eqs.(12) to (15) are the Prandtl number Pr,the Schmidt number Sc,the ratio of the diffusion coefficients δ,the strength of the homogeneousKand the heterogeneousKsreactions,and the stretching/shrinking parameterλ,and they are given as:

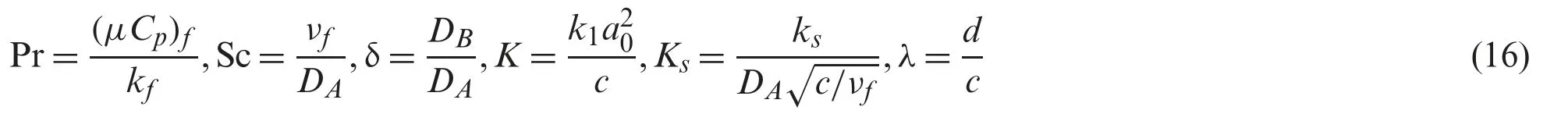
Note that,λ＜0 andλ＞0 are for the shrinking and stretching sheets,respectively,whileλ=0 designates the static sheet.As discussed by Chaudhary and Merkin [8],both diffusion coefficients(DAandDB) are of comparable sizes,thus,these coefficients are assumed to be equal by taking δ=1.Hence,one gets:

Using Eq.(17),Eqs.(13) and (14) become:

subject to:

The skin friction coefficientCfand the local Nusselt numberNuxare defined as:

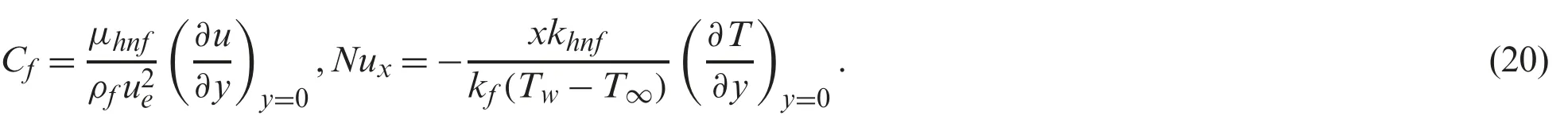
Using the similarity variables (9),one obtains

whereRex=uex/νfis the local Reynolds number.

3 Temporal Stability Analysis

The stability of the dual solutions over time is studied.This analysis was first introduced by Merkin [45]and then followed by Weidman et al.[46].Firstly,consider the new variables as follows:

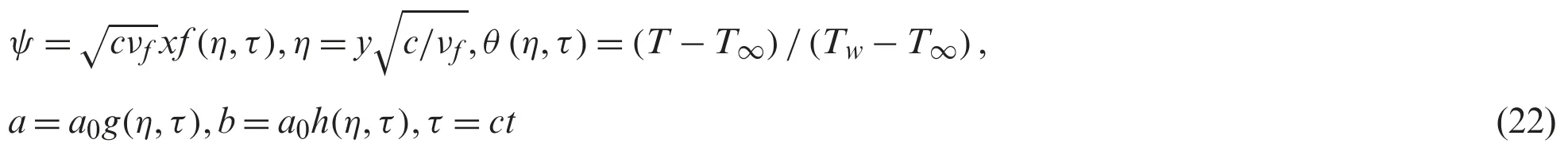
Now,consider the unsteady form of Eqs.(4) to (7) while Eq.(3) remains unchanged.On using (22),one obtains:

subject to:

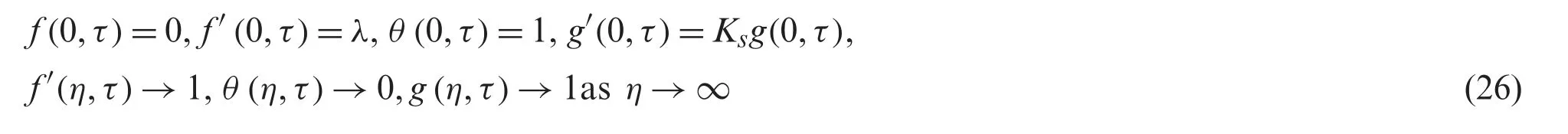
Then,the disturbance is applied to the steady solutionsf=f0(η),θ=θ0(η),andg=g0(η)of Eqs.(11),(12) and (18) by employing the following relations [46]:

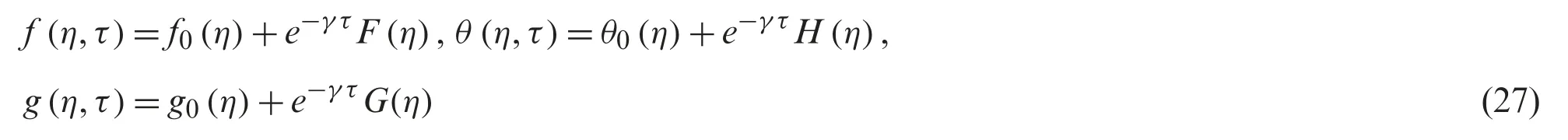
The sign (positive or negative) of the eigenvalueγdetermines the stability of the solutions.Also,F(η),H(η),andG(η)are relatively small compared tof0(η),θ0(η),andg0(η).On using Eq.(27),and after linearization,Eqs.(23) to (25) become:

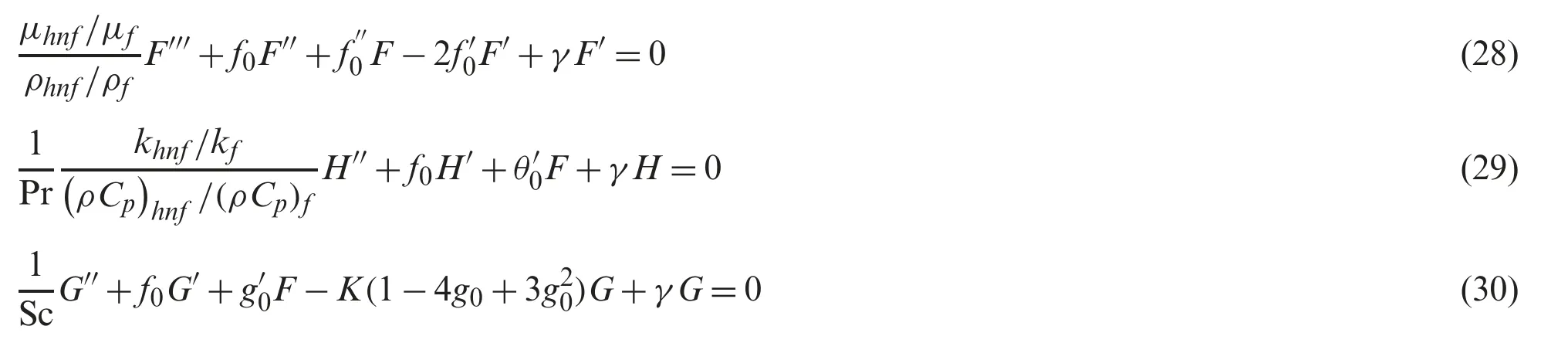
subject to:

The quantityF′′(0)is fixed in order to obtainγin Eqs.(28) to (30).Without loss of generality we takeF′′(0)=1,see also [48].

4 Results and Discussion

By utilising the package bvp4c in MATLAB software,Eqs.(11),(12),and (18) subjected to Eqs.(15) and (19) are solved numerically.In particular,bvp4c is a finite-difference code that implements the three-stage Lobatto IIIa formula [49].This is a collocation formula that provides a continuous solution with fourth-order accuracy.Mesh selection and error control are based on the residual of the continuous solution.The effectiveness of this solver ultimately counts on our ability to provide the algorithm with an initial guess for the solution.Because the present problem may have multiple (dual) solutions,the bvp4c function requires an initial guess of the solution for Eqs.(11),(12),and (18).Using this guess value,the velocity,temperature and the concentration profiles must satisfy the boundary conditions (15) and (19) asymptotically.Determining an initial guess for the first solution is not difficult because the bvp4c method will converge to the first solution even for poor guesses.However,it is rather difficult to determine a sufficiently good guess for the second solution of Eqs.(11),(12),and (18).Also,this convergence issue is influenced by the value of the selected parameters.In this study,the relative tolerance was set to 10－10.To solve this boundary value problem,it is necessary to first reduce the equations to a system of first-order ordinary differential equations.Further,the effect of several physical parameters on flow behaviour is examined.The total composition of Al2O3and Cu volume fractions are applied in a one-to-one ratio.For instance,1% of Al2O3(φ1=1%)and 1% of Cu(φ2=1%)are mixed to produce 2% of Al2O3-Cu hybrid nanoparticles volume fractions,i.e.,φhnf=2%.

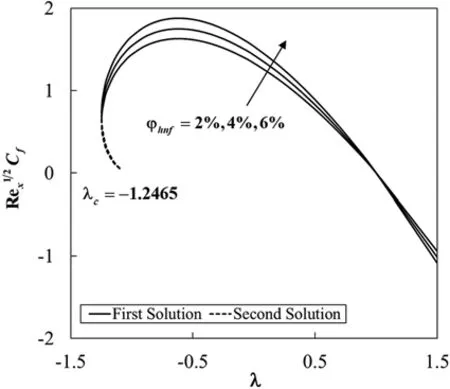
Figure 2:Variation of the skin friction Re1/2x Cf against λ for different values of φhnf

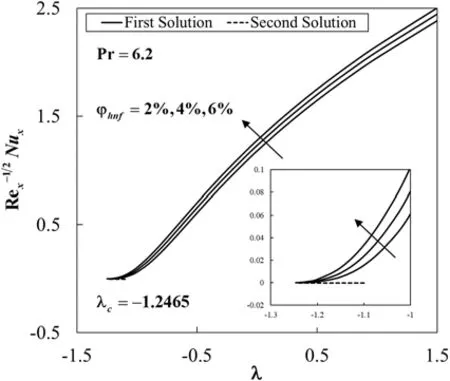
Figure 3:Variation of the local Nusselt number Re－1/2x Nux against λ for different values of φhnf

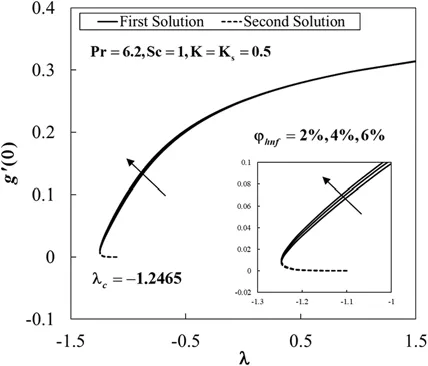
Figure 4:The concentration gradient at the surface g′(0) against λ for various values of φhnf

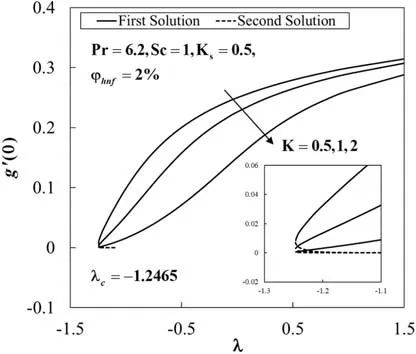
Figure 5:The concentration gradient at the surface g′(0) against λ for various values of K

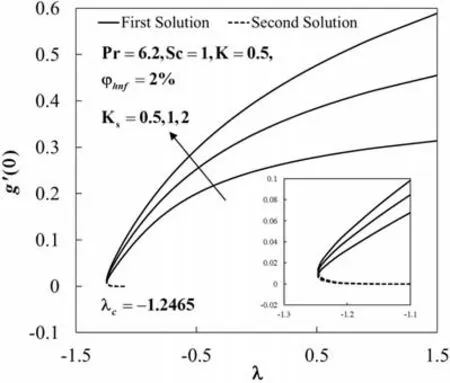
Figure 6:The concentration gradient at the surface g′(0) against λ for various values of Ks

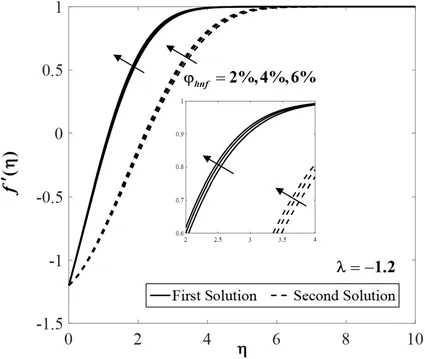
Figure 7:Velocity profiles f′(η) for various values of φhnf

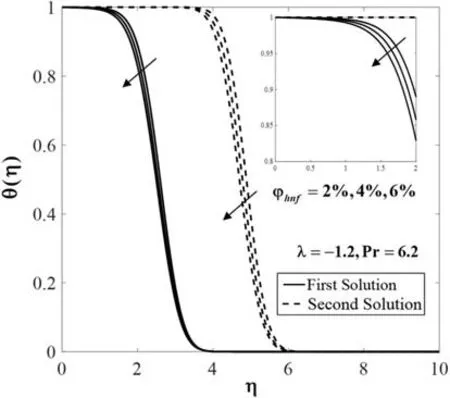
Figure 8:Temperature profiles θ(η) for various values of φhnf

The values of species concentration on the surfaceg(0)are compared with Khan and Pop [11]for various values ofKandKswhenφhnf=0 (regular fluid),Sc=1,andλ=0 (static sheet).It is found that the results are comparable for eachKandKsconsidered,as shown in Tab.3.Also,Tab.4 shows the comparison ofRe1/2x CfandRe－1/2x Nuxwith Waini et al.[47]when Pr=6.2 for different values ofλandφ2for Cu/water(φ1=0).It is noted that the present results are comparable with that mentioned literature.Next,Tab.5 displays the values ofRe1/2x Cf,Re－1/2x Nuxandg′(0)for Al2O3-Cu/water with various values of parameters whenSc=1 and Pr=6.2.The rising ofφhnftends to upsurge the values of these physical quantities.These behaviours also can be seen in Figs.2 to 4.This finding is consistent with the fact that the added hybrid nanoparticles improve the heat transfer rate due to synergistic effects as discussed by Sarkar et al.[39].Besides,the increasing ofλleads to enhance the values ofRe－1/2x Nuxandg′(0),but the values ofRe1/2x Cfis declining withλ.Also,the rise ofKdeclines the values ofg′(0),whereas the effect of largerKsis to enhance the values ofg′(0).However,the values ofRe1/2x CfandRe－1/2x Nuxare not affected by these parameters.At the same time,Figs.5 and 6 show the variations ofg′(0)againstλwith the effect ofKandKs.On the other hand,dual solutions are obtained for a limited range ofλas shown in Figs.2 to 6.The bifurcation of the solutions occurs atλc=－1.2465 for all considered parameters.

Table 3:Values of g(0) for various values of K and Ks when φhnf=0 (regular fluid),Sc=1,and λ=0 (static sheet)

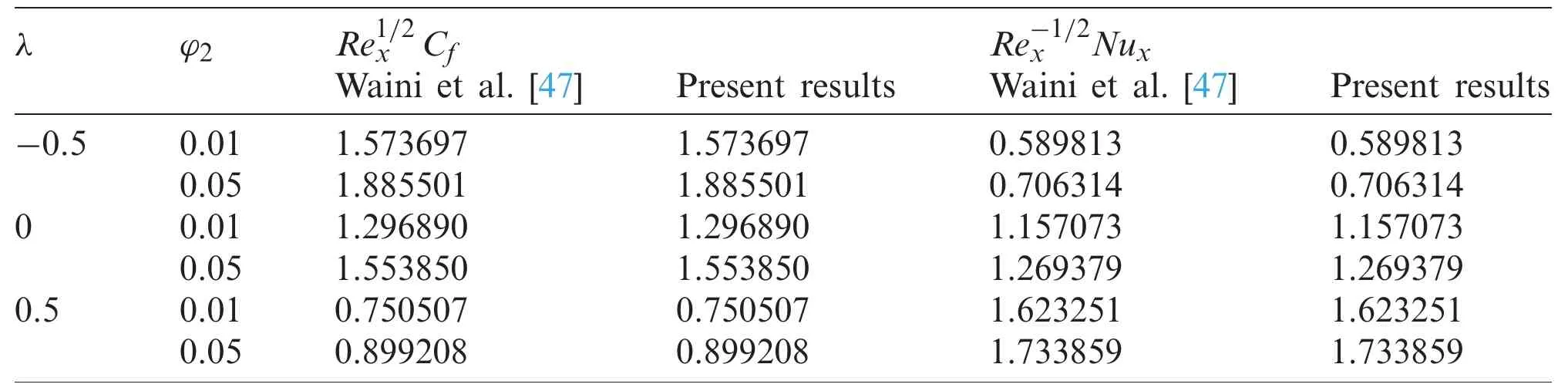
Table 4:Values of Re1/2x Cf and Re－1/2x Nux for different values of λ and φ2 when Pr=6.2 and φ1=0 (Cu/water)

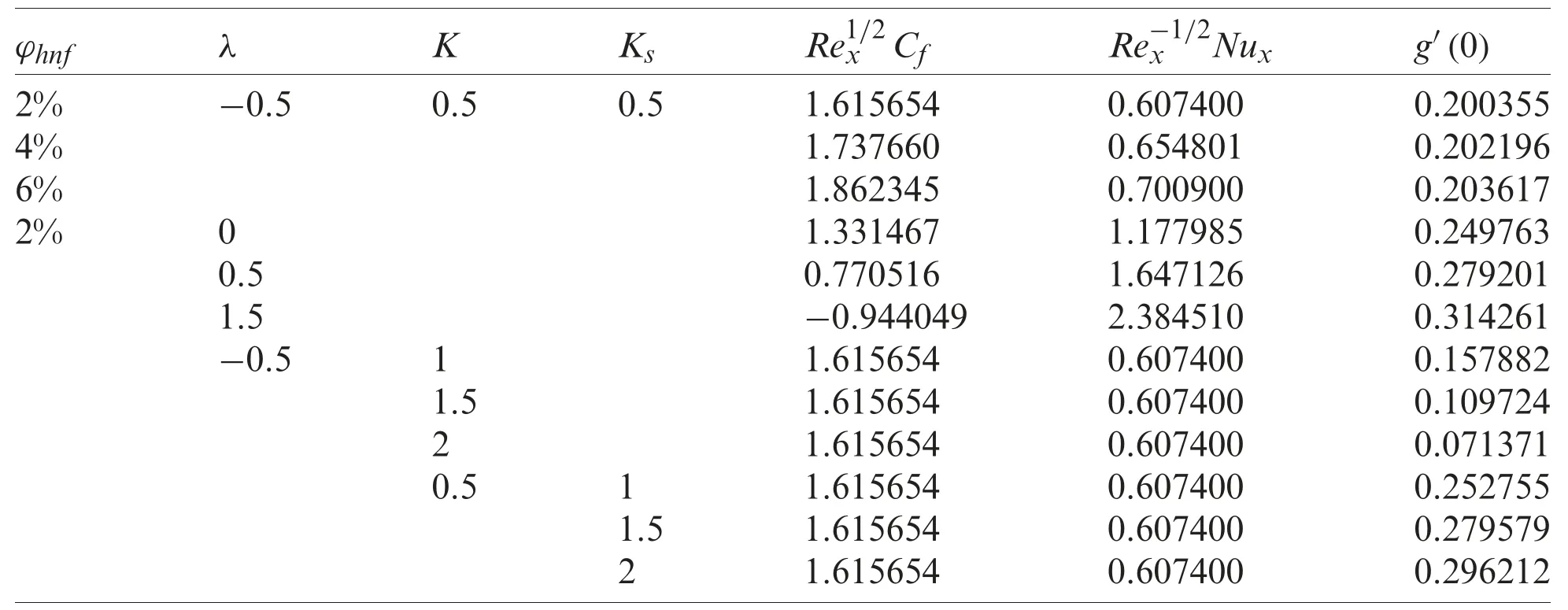
Table 5:Values of Re1/2x Cf,Re－1/2x Nux,and g′(0) for Al2O3-Cu/water with various values of parameters when Sc=1 and Pr=6.2

Further,Figs.7 to 9 display the effect ofφhnfonf′(η),θ(η)andg(η)whenλ=－1.2,6.2,Sc=1,andK=Ks=0.5.It is seen that both branch solutions off′(η)andg(η)show an increasing pattern for higher compositions ofφhnf.Meanwhile,the temperatureθ(η)declines for both branch solutions.Physically,the addition of the nanoparticles increases the viscosity of the fluid and thus slowing down the fluid motion.Also,the added nanoparticles dissipate energy in the form of heat and consequently exert more energy which enhances the temperature.

The effects ofKandKson the concentrationg(η)whenλ=－1.2,Pr=6.2,Sc=1 andφhnf=2% are depicted in Figs.10 and 11,respectively.The decreasing pattern of concentration on both branch solutions is observed.It is consistent with the fact that the reaction rate increases as the values ofKandKsincrease,which cause the reduction in the diffusion rate.

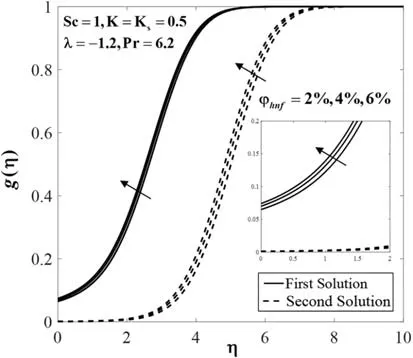
Figure 9:Concentration profiles g(η) for various values of φhnf

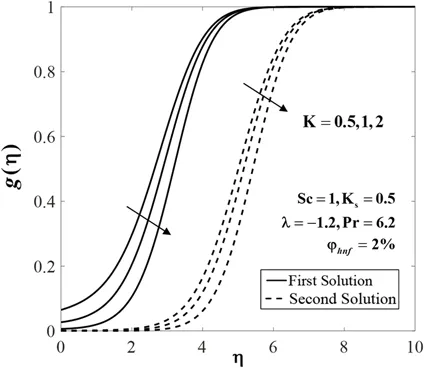
Figure 10:Concentration profiles g(η) for various values of K

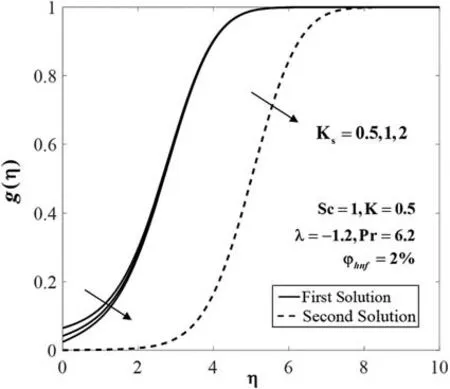
Figure 11:Concentration profiles g(η) for various values of Ks

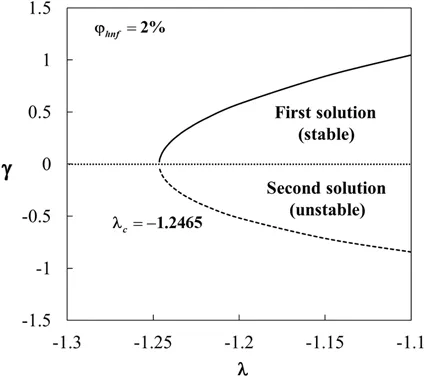
Figure 12:Eigenvalues γ against λ

The variations of the eigenvaluesγagainstλwhenφhnf=2% are portrayed in Fig.12.For the positive values ofγ,it is noted thate－γτ→0 as time evolves(τ→∞).In contrast,for the negative values ofγ,e－γτ→∞,which shows an increasing of disturbance over time.These behaviours show that the first solution is stable and physically reliable,while the second solution is unstable in the long run.

5 Conclusion

The stagnation point flow of Al2O3-Cu/water hybrid nanofluid over a stretching/shrinking sheet was studied.Both homogeneous and heterogeneous reactions were considered.Findings revealed that dual solutions appeared for some ranges of the shrinking strengthλ.The solutions were obtained up to a certain critical value ofλ(＜0),in the shrinking region.The increment of the skin friction coefficientRe1/2x Cf,local Nusselt numberRe－1/2x Nux,and the concentration gradient at the surfaceg′(0)were observed with the rise of the nanoparticles volume fractionsφhnf.The values ofg′(0)decreased for larger values ofK,but increased with the rise ofKs.Finally,it was discovered that two solutions were obtained for a single value of parameter.Further analysis showed that only one of these solutions is stable and thus physically reliable over time.

Acknowledgement:We acknowledge the Universiti Teknikal Malaysia Melaka and the Universiti Kebangsaan Malaysia (DIP-2020-001) for financial supports.

Funding Statement:This research was funded by Universiti Kebangsaan Malaysia (Project Code:DIP-2020-001).

Conflicts of Interest:The authors declare that they have no conflicts of interest to report regarding the present study.