一种新型足式爬壁机器人设计

霍 平，徐阳阳，于江涛，王亚州

（1.华北理工大学机械工程学院，河北唐山 063210；2.河北省工业机器人产业技术研究院，河北唐山 063210）

0 引言

随着国家经济快速发展，工业中的大型油罐、钢结构及船舶等应用越来越广泛，属于长期作业设备，需要定期对其进行检修，人工工作环境恶劣，存在安全隐患且作业效率低。对此，国内外学者开始设计研发爬壁机器人［1-5］，使其代替人工完成作业。

本文针对船舶、大型罐体等大型金属表面进行除锈、清洗、打磨等作业，设计一种新型框架足式爬壁机器人，与其他爬壁机器人设计不同［6-9］，该爬壁机构的运动具有较好的直线性、平稳性，且能够根据障碍物的大小、宽窄自动调节其迈步跨度和高度。

1 爬壁机器人整体结构设计

1.1 行走结构设计

行走机构是机器人的关键部件，不仅要求腿部结构简单、运动精度高，还要求有较高的稳定性，满足机器人的各项作业要求。本文的行走机构是仿人腿部，设计为左腿和右腿结构，既要保证机器人运动的稳定性，又要实现灵活、越障等优点。腿部结构设计成一种伸缩移动式结构，如图1 所示。为保证机器人爬行过程结构紧凑，左、右腿分别对称排列在本体框架两侧，腿部结构等效成一个等腰梯形的平面连杆机构，每条腿上有6 根拉杆，其中双拉杆与单拉杆成对角分布，分别与前、后滑块和底座连接，确保足部与本体框架、机器人与作业壁面所处平面始终保持水平，提高机器人的稳定性。

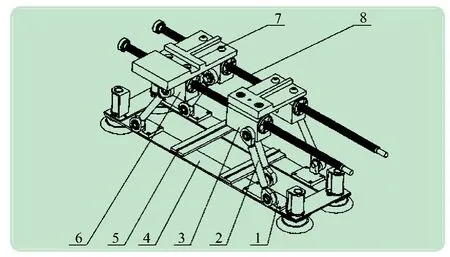
图1 爬壁机器人腿部结构示意图

1.2 传动机构设计

传动机构是爬壁机器人的核心部分，决定着机器人的运动精度、工作效率和工作质量，保证机器人的工作效率。爬壁机器人传动机构示意图如图2 所示。

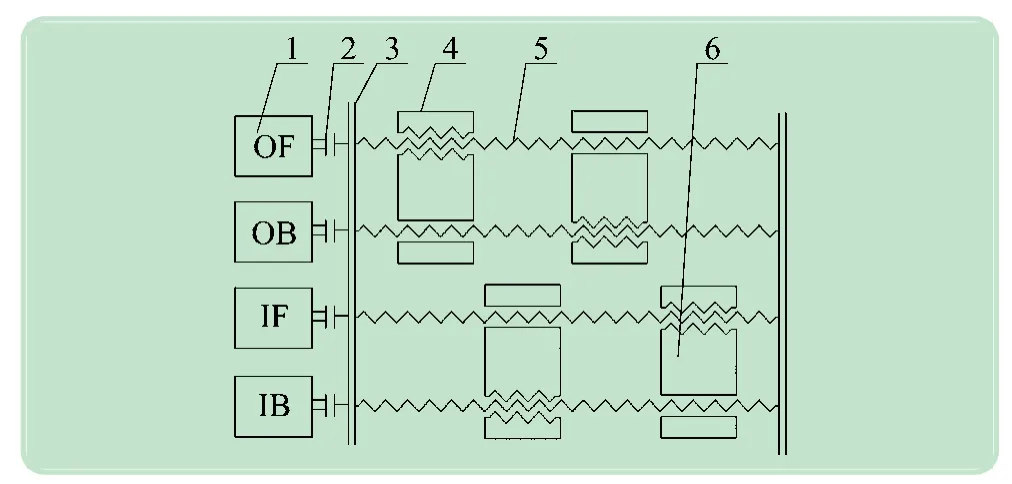
图2 爬壁机器人传动机构示意图

本机构采用并联方式，腿部结构分布在本体框架两侧，丝杠一端与电机组连接；另一端与本体框架连接。前、后滑块中一组对角孔设有螺纹，与丝杠形成螺旋副并起传动作用；另一组设为通孔，与丝杠形成移动副。

1.3 整体结构设计

虚拟样机模型是验证设计可行性的重要环节，使用SolidWorks软件设计各部件模型，并完成机器人模型的装配。新型足式爬壁机器人整体结构如图3 所示，机器人本体框架长410 mm，宽265 mm，腿部结构伸缩范围95～140 mm。

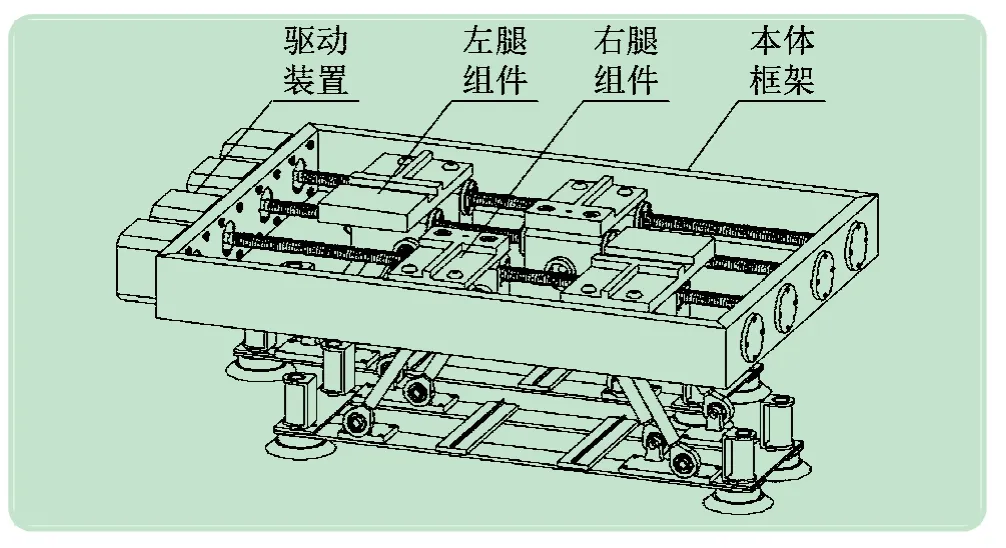
图3 足式爬壁机器人整体结构

机器人整体结构采用铝合金材料，既降低自重，又满足刚性要求。底板和连接板其中一表面加工为带棱，即提高足部刚性和稳定性，又不易发生变形。左右两腿部结构设计成对称结构，便于安装和步态规划，且运动原理相同。通过驱动装置调节转速改变前、后滑块间的距离，调整迈步间距和高度，实现机器人抬腿与落腿动作。当两滑块间距离增大时，足部落脚吸附在壁面上；两滑块距离减小时，足部抬起向前移动。两足依次交替吸附在壁面上行走，类似人走路运动，具有良好的直线运动和越障能力。

2 稳定性分析

首先建立稳定平面，当机器人重心投影到稳定平面时，处于稳定状态，可能会沿壁面滑动；相反，重心落在稳定平面外时，可能会壁面滑动，也可能发生倾覆［10-11］。如图4 所示，底座在竖直方向的投影面α 为该状态的稳定平面。如果机器人绕一点发生倾覆，则角θ为机器人重心与该点连线与机器人底座平面的夹角。其中，β 为机器人足底平面与竖直方向的夹角。当机器人重心G的投影点落在α 内时，即θ≤β，机器人处于稳定状态；当机器人重心G落在α外时，即θ ＞β，机器人处于非稳定状态。

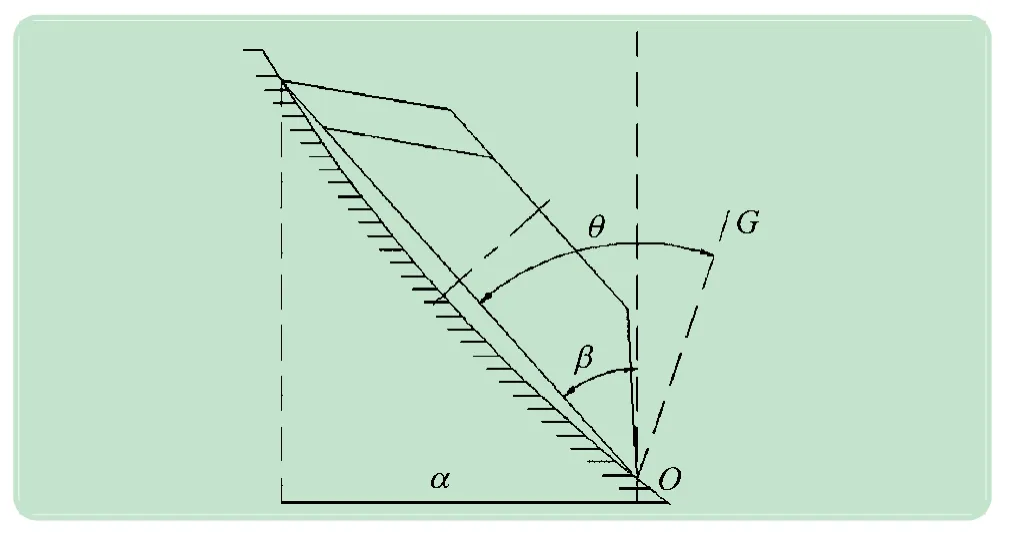
图4 机器人稳定平面

爬壁机器人在壁面上不同位置的曲率发生变化，其位姿也在变化，机器人的稳定平面也在不断变化。机器人随时可能由稳定状态进入非稳定状态。处于稳定状态时，仅考虑合外力的平衡，磁力平衡自身重力产生沿壁面的下滑力和壁面对机器人的支持力；处于非稳定状态时，既要考虑机器人所受的合外力，也要考虑合外力矩，故磁力需要平衡下滑力、持力和平衡倾覆力矩。

3 受力分析

3.1 抗滑落分析

为避免机器人在壁面上下滑动，要求吸附装置与壁面间的静摩擦力足够大，最大静摩擦力取决于支持力，支持力又取决于吸附力［12-13］。故合理规划机器人所有位姿所需吸附力、静摩擦力平衡机器人的下滑力。机器人在壁面作业时，设自身的倾角为α，水平面上倾角为0，分为两种情况：①在壁面上方运动，有（0°≤α≤90°）；②在壁面下方运动，有（90° ＜α≤180°）。

3.1.1 壁面上方运动

机器人在壁面上方运动时（0°≤α≤90°），对其任意时刻进行受力分析，如图5 所示。

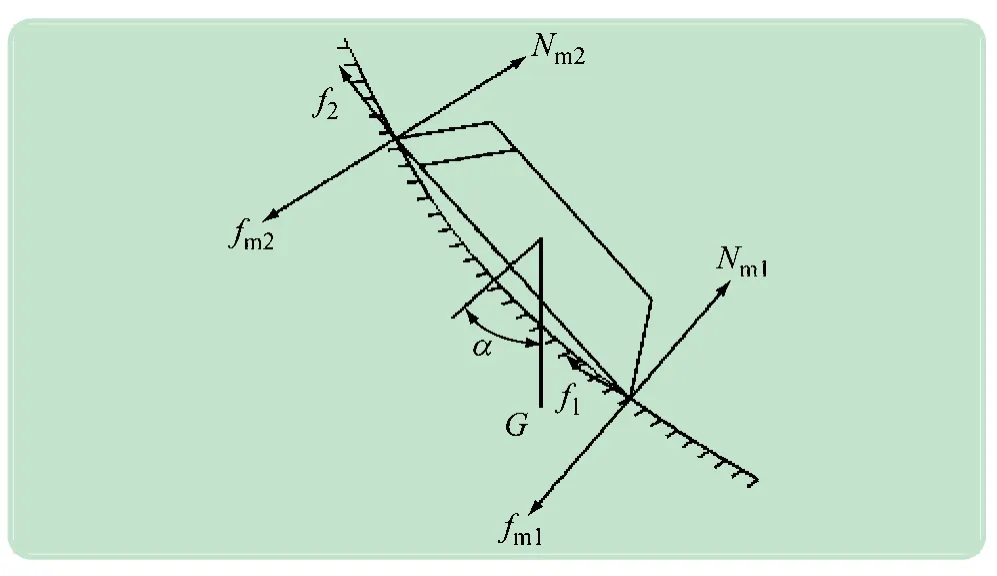
图5 机器人在上壁面工作受力分析

机器人不发生滑落的条件是，足部吸附单元与壁面间的最大静摩擦力大于自身重力沿壁面的向下分量。取吸附单元与壁面间摩擦因数的最小值，平衡方程为：

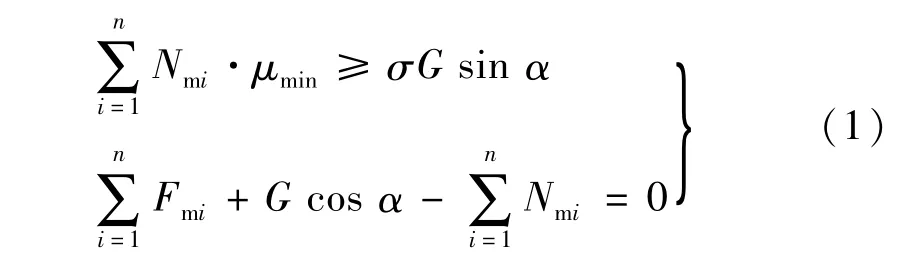
式中：G为爬壁机器人本体质量，G=150 N；Nm为作业面对单个磁铁的支持力；σ为安全系数，σ=2；Fm为单个磁铁与壁面间的吸附力；n为磁铁的个数，n=4；μmin为磁铁与壁面之间的最小摩擦系数，μmin=0.1；α为机器人在壁面工作时的倾斜角度。

作业表面是不完全平整且存在曲率，故需要对作业平面进行简化，取Fmi与竖直方向的夹角为α，整理可得：

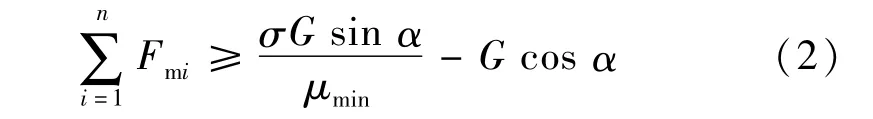
解得：

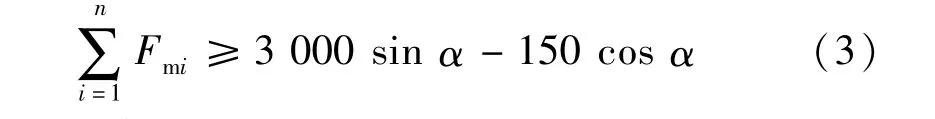
故单个吸附单元所需的吸附力为

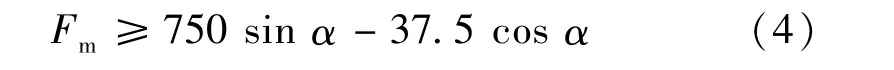
通过MATALB进行绘图，得到机器人在上壁面运动时，单个吸附单元所需的吸附力与机器人倾斜角α间的关系如图6 所示。

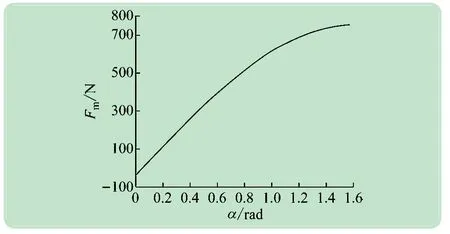
图6 单个吸附单元所需吸附力与倾斜角度间的关系

随着工作壁面倾斜角度的增大，机器人所需的吸附力逐渐增大，使最大静摩擦力抵消重力产生的下滑力。当机器人倾斜角度达到90°时，此时所需吸附力最大Fm=750 N。

3.1.2 壁面下方运动

爬壁机器人在壁面下方运动时（90° ＜α≤180°），对其任意时刻进行受力分析，如图7 所示。

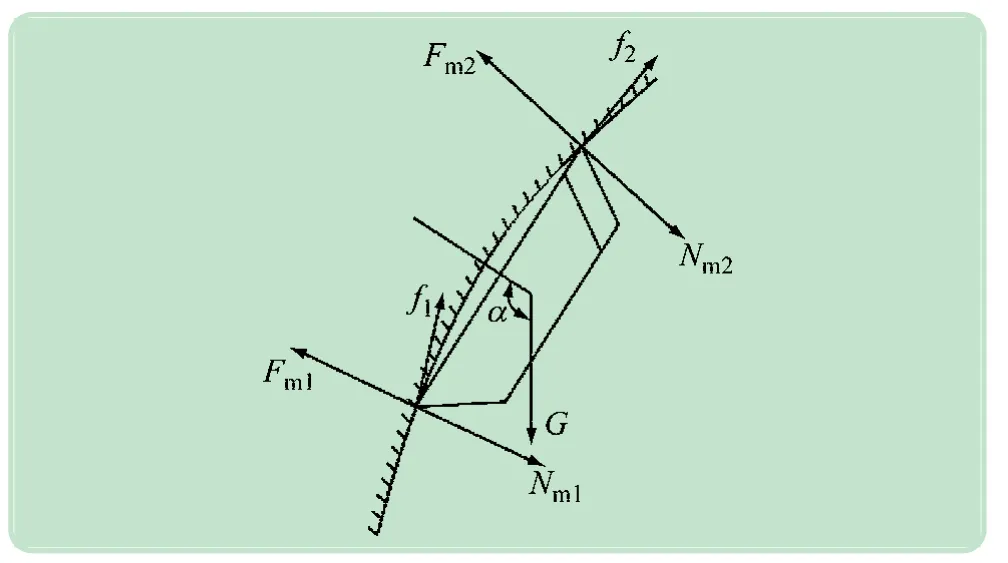
图7 机器人在下壁面工作受力分析

平衡方程为

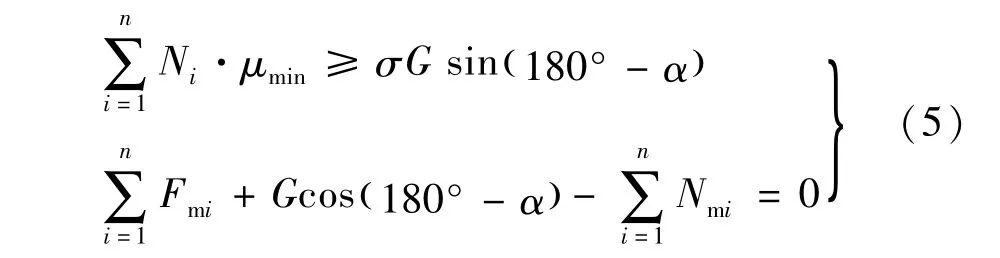
整理得

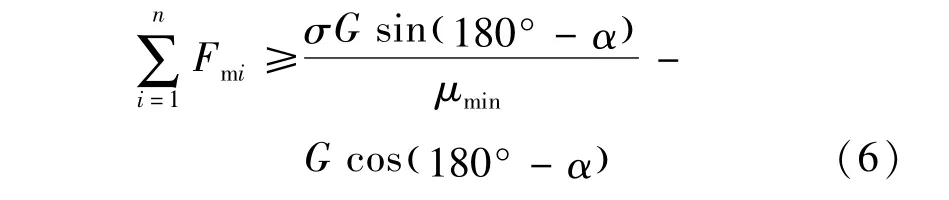
故单个吸附单元所需的吸附为

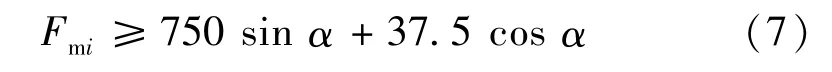
当机器人在下壁面运动时，单个吸附单元所需吸附力与壁面倾角α间的变化如图8 所示。

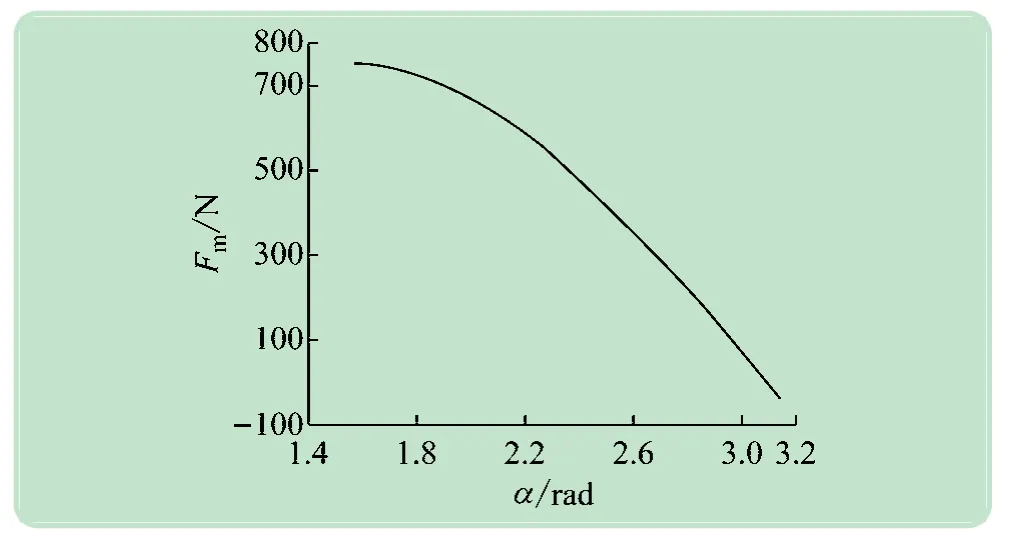
图8 机器人下壁面运动时单个吸附单元所需吸附力与α关系

随着工作壁面倾角的不断增大，吸附单元所需吸附力减小。当α=90°时，所需吸附力达到最大临界值Fm=750 N。因此，无论机器人处于任何位姿时，单个吸附单元与壁面间的吸附力大于临界值（750 N），保证机器人不会发生滑落。

3.2 抗倾覆分析

机器人重力分解为沿壁面向下和垂直壁面向下的两个分量［13-14］。在上壁面作业时，重心随着壁面的倾斜程度增加发生失稳状态，垂直壁面的分量产生抗倾覆力矩；在下壁面作业时，两个分量全部产生倾覆力矩。以机器人在下壁面作业为例，对其进行抗倾覆分析。

3.2.1 向前、向后倾覆分析

发生倾覆的位置可能为足部前端或后端的一边，近处的吸附单元产生的抗倾覆力矩为零，远处的吸附单元产生抗倾覆力矩。根据力矩平衡条件∑M0=0，得平衡方程：

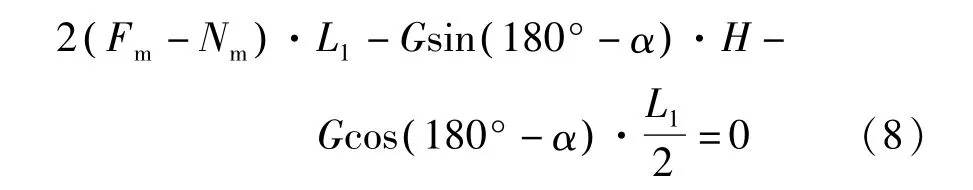
式中：Fm为单个吸附单元壁面之间的吸附力；Nm为壁面对单个吸附单元的支持力；H为重心与壁面间的距离，H=173.20 mm；L1为机器人本体框架的长度，L1=400 mm。

取Nm=0 的临界条件，得：

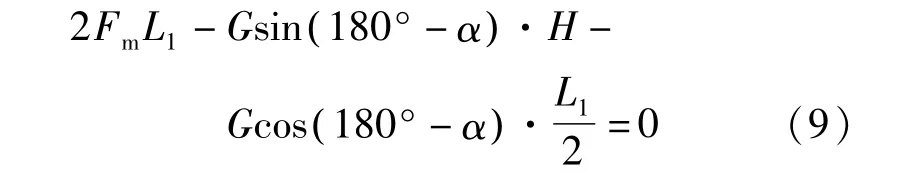
已知两个投影的吸附单元为O′点，则单个吸附单元的吸附力应满足：

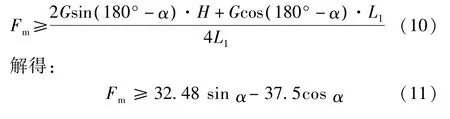
机器人在下壁面运动（90°≤α≤180°），且不发生向前或向后倾覆时，单个吸附单元所需吸附力Fm随倾角α的变化如图9 所示。图中，α=122°时，吸附单元所需吸附力达到临界值Fm=49.61 N，故吸附力Fm＞49.61 N。

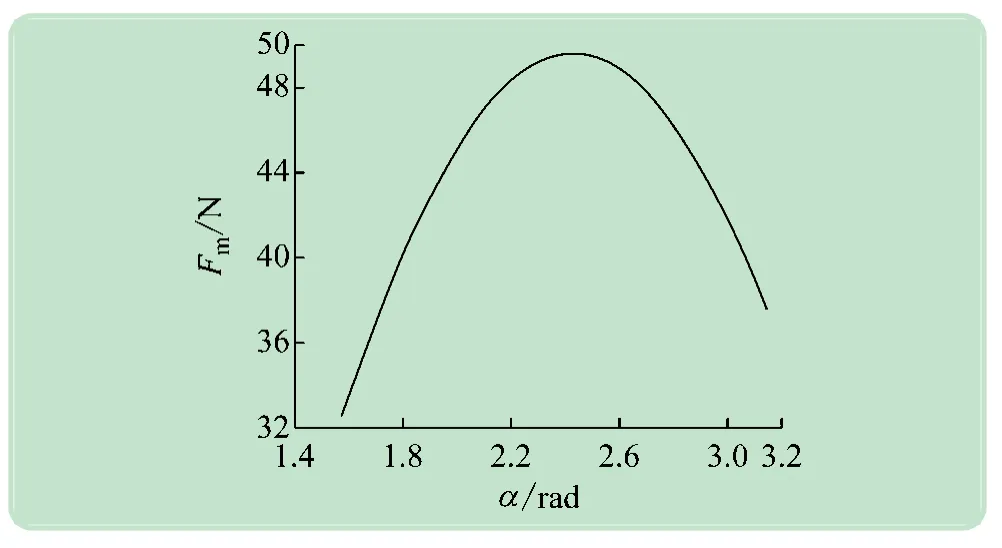
图9 单个吸附单元的吸附力随α关系

3.2.2 向左、向右倾覆分析

发生倾覆的位置可能是机器人足底左端或右端的一边，远端的吸附单元产生抗倾覆力矩［15］。得平衡方程：

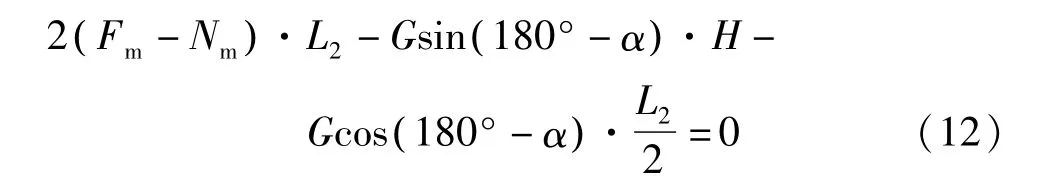
式中：L2为机器人本体框架的宽度，L2=300 mm。取Nm=0 的临界条件，并带入数值，得到单个吸附单元的吸附力为

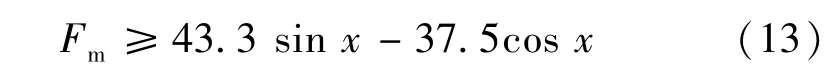
机器人在下壁面运动（90°≤α≤180°），且不发生向左或向右的倾覆时，单个吸附单元所需吸附力Fm随倾斜角度α的变化如图10 所示。

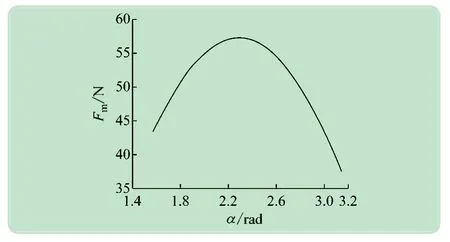
图10 单个吸附单元的吸附力随α关系

图中，α=130°时，所需的吸附力达到临界值Fm=57.28 N。为避免爬壁机器人发生向左或向右倾覆，其足部单个吸附单元所需的最小吸附力为57.28 N，故吸附力Fm≥57.28 N。

机器人发生滑落对单个吸附单元的吸附力为750 N，远大于发生倾覆的单个吸附单元吸附力57.28 N。所以，机器人在作业壁面易发生滑落，故对单个吸附单元设定时，以发生滑落的临界条件为依据。由于作业壁面环境复杂多变，提高爬壁机器人作业稳定性，增加单个吸附单元与壁面间的磁吸附力为1.5 倍，故Fm=1 125 N。

4 试 验

通过SOLIDWORKS 软件建立新型足式爬壁机器人三维模型，进而搭建爬壁机器人样机模型，进行实验验证机器人设计的合理性及可行性。机器人运动示意图如图10 所示，每两幅图分别为机器人的正面和侧面，能够更加清晰地表达机器人的运动过程。进行本体框架做腿部的相对运动，回到图（a）所示位置为运动结束。

图11 机器人运动图

实验结果表明，该机构能够实验预期的越障功能，可以根据障碍物调节抬腿高度和迈步间距。此外，该机构具有良好的直线运动，满足大型壁面的作业要求。

5 结语

本文提出了一种新型足式爬壁机器人结构，由行走机构、吸附装置和传动机构组成。该机器人有良好的直线运动、较好的步态规划和较强的越障能力。通过对吸附装置进行受力分析，满足机器人所需吸附力的要求，保证机器人在壁面上不存在滑动和倾覆的风险。通过实验验证了机器人本体结构设计的合理性及腿部结构的可行性，且本体框架与壁面始终保持平行。证明该爬壁机器人有能力在垂直壁面上攀爬。