基于超载法的碾压混凝土拱坝非线性有限元研究

(江西省水利水电建设有限公司，江西 南昌 330025)

1 引 言

拱坝是具有自身应力调节能力的多重超静定结构。在加载过程中，拱坝的破坏是逐渐发生的。局部开裂后，拱坝仍保持一定的承载力，直至发生极限破坏为止。拱坝的地质条件复杂且荷载巨大，因此有必要在施工之前进行详细的稳定性分析。传统的拱坝分析方法，如刚体极限平衡法，是基于线性弹性计算，没有充分考虑拱坝与地基的相互作用。随着数值方法的发展，有限元法[1-2]、边界有限元法[3]、扩展有限元法[4]、离散元法[5-6]和数值流形法[7]被广泛应用于拱坝的分析。通过这些数值方法，可以对拱坝和基础[8-9]进行整体分析，也可以对局部裂缝进行细致的研究。本文基于超载法[10-11]对某碾压混凝土拱坝[12-13]坝体进行了非线性有限元[14]研究，采取逐步增加库水容重的方法，进行逐步的非线性分析，通过对变形、屈服区随超载倍数增加演化过程的分析，确定超载安全系数，掌握坝体系统的安全储备能力。研究结果表明，该方法计算得到的坝体的超载系数较安全，可为今后类似工程提供借鉴。

2 水文气象及工程资料

2.1 水文气象条件

锦江流域属中亚热带温暖湿润气候区，气候受季风控制，四季分明。气温变化特点为冬冷夏热，秋温高于春温；冬季盛行西北风，干而冷；夏季多东南、西南风，温而暖。

据上高气象站1981—2013年实测资料统计，流域多年平均气温17.9℃，极端最高气温40.8℃，出现在2003年8月，极端最低气温-10.0℃，出现在1991年12月。多年平均风速0.8m/s，最大风速23.6m/s，发生于1994年10月。多年平均相对湿度79.69%，多年平均无霜期273天，多年平均日照1549h，多年平均蒸发量(E601)1274.7mm。

据上高站1951—2013年共63年实测降水资料统计，流域多年平均降水量1673mm，降水量年际变化大，最大年降水量2369mm(1954年)，年最小降水量1028mm(1968年)，相差一倍多。降水量年内分配不均，汛期4—6月降水量占全年的45.54%，枯水期10月至次年2月降水量仅占全年的23.1%。

2.2 工程资料

保丰水库地处上高县翰堂镇保丰村及钊田村附近，距县城约23km，水库所在河流为锦江二级支流斜口水，属锦江水系。原保丰水库位于翰堂镇下山村境内，距翰堂镇约5km，所在河流为赣江水系锦河支流。原佑塘水库地处翰堂镇钊田村境内，所在河流为赣江水系锦河斜口水支流钊田水。原保丰水库与佑塘水库紧密相邻，佑塘水库的1号副坝位于保丰水库库区尾端，两水库具备良好的连通条件。根据地形条件，拆除佑塘1号副坝，两库即连为一体，原保丰水库的主坝仍作为本工程的主坝。本次保丰水库扩建拟抬高现状主、副坝坝高，通过抬高正常蓄水位至84.0m，增加有效扩容，将其改造为中型水库，坝顶高程统一为86.8m(防浪墙顶高程88.0m);在垭口部位新建副坝，对现有已建坝体进行加高加固；增设保丰4号副坝、溢洪道、灌溉隧洞等建筑物。

工程扩建后，水库正常蓄水位为84.00m，水库总库容1524万m3，水库设计灌溉面积1.5万亩，其中规划烟田面积0.36万亩，水库向翰堂镇、芦洲乡辖区内6个行政村的大部分自然村及城区多年平均日供水0.51万m3，年供水量为186万m3。

工程区处于扬子准地台、江南台隆、乐平台陷的萍乡—高安凹褶断束构造单元之中，褶皱断裂均甚发育，尤以西端的宜春—萍乡一带，褶皱较为强烈。该碾压混凝土拱坝坝轴线河谷地形呈基本对称的“V”形，左岸坡角约49°，右岸约为41°，谷底宽约23m，水深 6.5～8.5m，覆盖层厚7.5～11.5m，河床基岩面高程1280m。

3 计算参数和有限元模型

根据相关设计资料，有限元计算的岩体物理力学参数、坝体物理力学参数、地震参数以及水位资料具体如下。

3.1 岩体物理力学参数

岩体物理力学参数见表1。

3.2 坝体物理力学参数

坝体物理力学参数见表2。

表2 大坝碾压混凝土力学性能试验成果

3.3 地震参数

该大坝工程作为2级挡水建筑物，取基准期50年超越概率10%的地震动参数作为设计地震参数，校核地震参数在设计地震基础上提高标准为50年超越概率5%的地震动参数(见表3)。

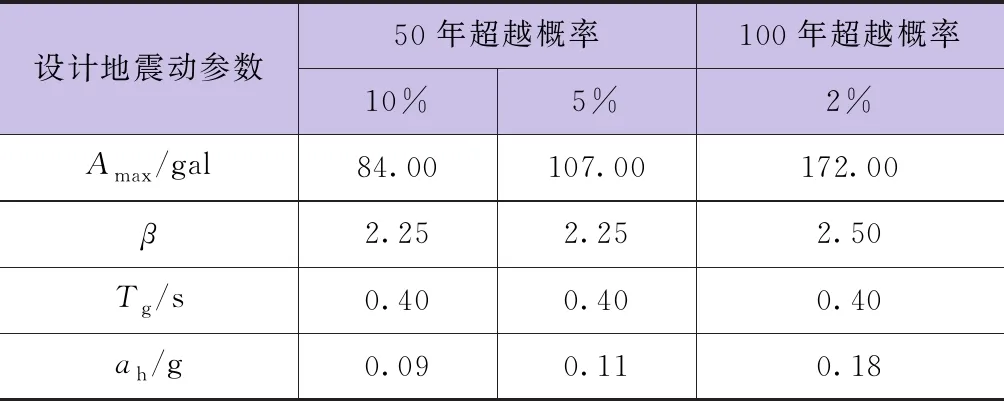
表3 场地基岩地震动参数计算值

3.4 水位资料

水位资料见表4。

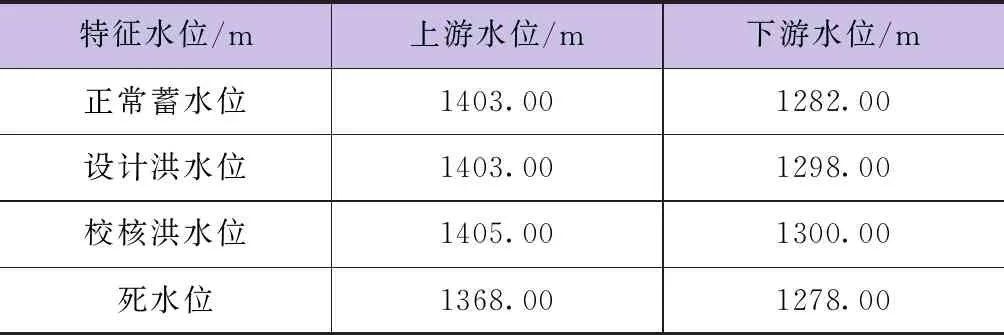
表4 特征水位

3.5 有限元模型及计算方案

有限元模型采用8节点6面体单元进行离散，有限元网格及材料分区情况见图1，共有363472个节点和262743个单元。计算方案采取超载库水容重的方法，进行非线性有限元计算，以正常蓄水位(1倍容重)为基础，依次取1.5、2.0、2.5、3.0、3.5、4.0、4.5、5.0、5.5……，直至不能计算为止，以此来考察拱坝的安全储备能力。

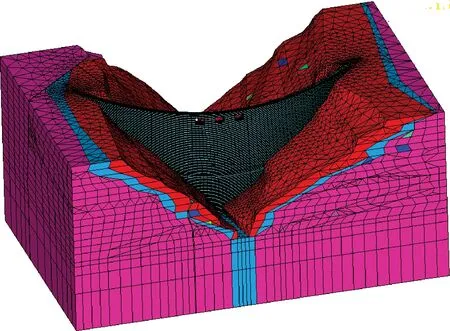
图1 有限元网格及材料分区

4 正常蓄水位坝体非线性结果

4.1 变形

图2为正常蓄水位坝体的位移云图，图2(a)为上游面x向位移云图，图2(b)为下游面y向位移云图，图2(c)为拱冠梁剖面z向位移云图，图2(d)为1280m高程平切面z向位移云图。

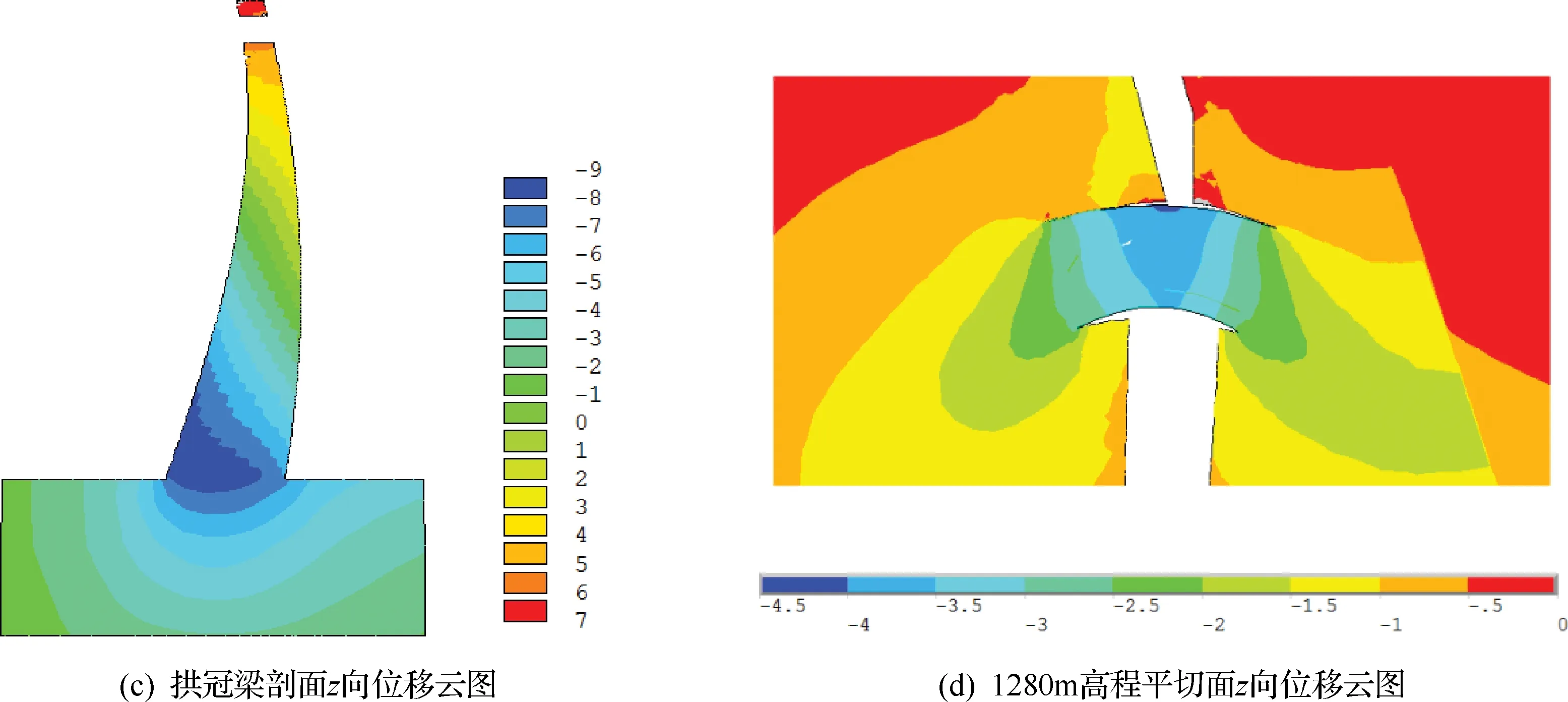
图2 位移云图

4.2 应力

图3为正常蓄水位坝体的应力云图，图3(a)为上游面x向应力云图，图3(b)为下游面y向应力云图，图3(c)为拱冠梁剖面z向应力云图，图3(d)为1280m高程平切面z向应力云图。

图3 应力云图

4.3 屈服区(点安全系数)

图4为点安全系数图，图4(a)为坝体点，图4(b)为1倍超载下坝体下游面点，图4(c)为建基面点，图4(d)为拱冠梁剖面点。

图4 点安全系数

5 超载计算结果

5.1 变形及应力

表5为坝体坝肩特征部位顺河向位移随超载系数变化的统计值，由表5可以看出，随着超载系数的增加，位移值显著增大。

表5 特征点顺河向位移随超载系数变化统计 单位：mm

为了考察建基面铅直向拉应力随超载系数增加向下游延伸范围的变化情况，统计了1280m高程(河床坝段建基面)自坝踵向下游的铅直向应力随超载系数增加而增加的情况，结果见表6。

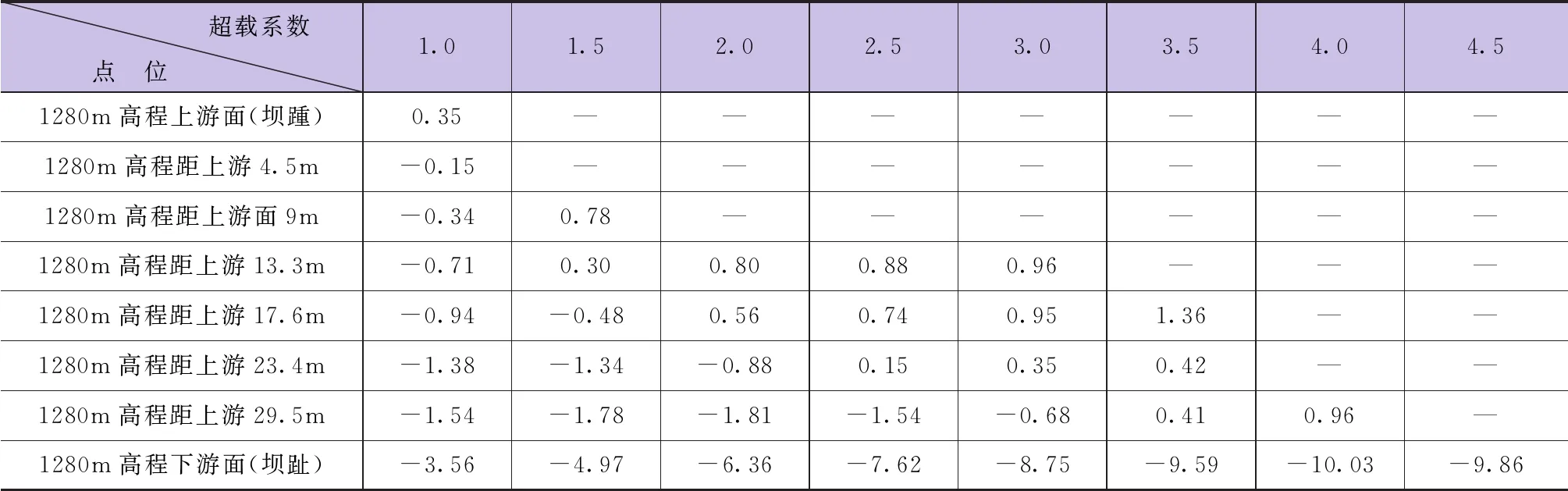
表6 特征点z向应力随超载系数变化统计 单位：mm

5.2 屈服区(点安全系数)

不同超载倍数下大坝不同位置点安全系数分布规律见图5～图13，图中灰色区域表示点安全系数小于1.0，即屈服区。

图5 1.5倍超载下坝踵、坝体下游、坝肩、拱冠梁安全系数分布

图6 2倍超载下坝踵、坝体下游、坝肩、拱冠梁安全系数分布

图7 2.5倍超载下坝踵、坝体下游、坝肩、拱冠梁安全系数分布

图8 3倍超载下坝踵、坝体下游、坝肩、拱冠梁安全系数分布

图9 3.5倍超载下坝踵、坝体下游、坝肩、拱冠梁安全系数分布

图10 4倍超载下坝踵、坝体下游、坝肩、拱冠梁安全系数分布

图11 4.5倍超载下坝踵、坝体下游、坝肩、拱冠梁安全系数分布

图12 5倍超载下坝踵、坝体下游、坝肩安全系数分布

图13 5.5倍超载下坝踵、坝体下游、坝肩安全系数分布

5.3 超载系数

在不同超载倍数下的坝体最大塑性顺河向位移见图14。

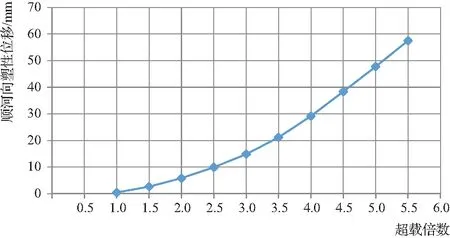
图14 顺河向塑性位移极值与超载倍数的关系

根据图14进行拟合曲线计算，并对图5～图13进行分析，可确定超载系数为3.1。

6 结 论

根据超载分析的计算结果，从应力及屈服区等方面分析其随超载系数增加的演化规律，可以得到如下认识：

6.1 位移

正常水位下坝体变形规律：横河向位移总体指向两岸，以拱冠梁为界左坝段指向左岸，右坝段指向右岸，左右坝段大致对称，横河向最大变形约为8mm，左岸略比右岸大；顺河向位移指向下游，坝顶附近最大，最大位移约为32mm；铅直向坝顶向上位移最大约为7mm，坝底向下位移最大约为9mm，其中坝底下游侧(坝趾)的量值比上游侧(坝踵)大。对比弹性与塑性计算结果，两者几乎没有差别，说明拱坝在正常水位下(1倍水载)总体处于弹性工作状态。

超载情况下坝体的变形规律与正常蓄水位下的规律一致，但量值随着超载系数的增加明显增大；从表5可以看出，坝体、坝肩等特征点的顺河向位移随着超载系数的增加逐渐呈非线性增加，且增加速率愈来愈大，见图14。

6.2 应力

正常水位作用下，坝体应力分布情况：坝踵存在拉应力区，拉应力区的范围为自坝踵向下游延伸约3m，小于坝体厚度的1/12，坝踵处最大拉应力约为0.4MPa，小于混凝土的抗拉强度；坝趾处于受压状态，最大压应力约为3.55MPa，小于混凝土及岩石的抗压强度；坝体下游面中高高程部位存在拉应力区，拉应力区向坝内延伸范围约在1m以内，最大拉应力约为0.3MPa；坝体应力总体上处于弹性状态。

超载情况下，坝体的应力分布规律与正常蓄水位的规律是一致的；随着超载系数的增加，正常水位下受拉的部位无论在量值还是范围方面均为扩大，坝踵部位的拉应力量值和范围显著增加，坝趾处的压应力量值也显著增加；当超载系数增加到3.0时，拉应力区自坝踵向坝趾延伸范围超过坝体厚度的1/2，坝趾处压应力量值接近9.0MPa；坝踵部位及坝体下游面中高高程部位处于拉剪区，坝趾及坝肩处于压剪区。

6.3 屈服区(点安全系数)

a.超载倍数为1.0、1.5、2.0、2.5、3.0、3.5、4.0、4.5、5.0、5.5时，坝体底面的屈服区、坝体下游面的屈服区、建基面的屈服区、拱冠梁剖面的屈服区演化规律分别见图5～图13。

b.由坝体底面屈服区的演化规律可知，超载系数在2.0以内时，坝体底面未出现明显屈服区，其点安全系数均在1.0以上；当超载系数为2.5时，坝体底面开始出现屈服区；随着超载系数的增加，屈服区的范围逐渐扩大，超载系数为3.5时，坝体底面的屈服区已非常明显。

c.由坝体下游面屈服区的演化规律可知，当超载系数为2.0时，坝体下游面中高高程部位和坝趾附件开始出现屈服区；随着超载系数的增加，屈服区的范围逐渐扩大，超载系数为3.0时，坝体下游面的屈服区已非常明显，且屈服区扩展范围接近下游面面积的一半。

d.由建基面屈服区的演化规律可知，当超载系数为2.5时，右岸坝肩岩体开始出现屈服区；当超载系数为3.0时，左岸坝肩岩体开始出现屈服区；随着超载系数的增加，建基面岩体的屈服区范围逐渐扩大，超载系数为3.5时，建基面岩体的屈服区已非常明显，且右岸坝肩岩体的屈服区范围比左岸坝肩岩体的屈服区范围大。

综上所述，超载系数在1.5时，坝体仍总体处于弹性状态，当超载系数等于2.0时，坝体 开始进入塑性状态；随着超载系数的增加，坝踵坝趾部位、坝体下游面中高高程部位、坝肩岩体的屈服区面积逐渐扩大，当超载系数增加到3.0以后，各部位屈服区范围显著；总体上坝踵部位的屈服区比坝趾先出现，右岸坝肩岩体的屈服区比左岸坝肩岩体先出现，且右岸的屈服区范围比左岸大，坝体中高高程部位下游面先出现屈服区并向四周及厚度方向逐渐扩大。

综合分析变形、应力及屈服区随超载系数的变化规律，得出坝体的超载系数在3.0以上，且拱效应偏弱。