图形公式教学中三个不可忽视的问题
2021-12-14刘兆伟
文∣刘兆伟
图形公式是“图形与几何”领域的重要内容。小学数学中的图形公式知识包括平面图形的周长、面积公式,立体图形的体积、表面积公式等。在这些内容的教学中,不仅要让学生通过探究得到公式,运用公式解决问题,而且要让学生在探究的过程中发展空间观念,感悟数学思想,积累数学活动经验。根据这几年的课堂观察,笔者发现大部分教师在图形公式教学中开始注重图形公式的探究过程,但仍以得到图形公式及熟练运用公式计算为主要教学目标,欠缺空间观念的培养、数学思想的感悟以及数学活动经验的积累。
一、不可忽视空间观念的培养
“图形与几何”领域教学的核心目标是培养学生的空间观念,这也应成为图形公式教学的核心目标。想象力是空间观念培养的关键,不管在图形公式的推导过程中,还是在图形公式的应用过程中,我们都可以让学生通过想象发展空间观念。
(一)在公式推导过程中,让学生通过想象发展空间观念
图形公式推导过程的本质是推理过程。借助符号进行的形式化推理过程过于抽象,而小学生的思维以形象思维为主,所以,如果仅仅借助推理得到一般化的图形公式,部分学生会难以理解。在推导图形公式的过程中,我们可以先让学生通过探究得到具体图形周长、面积或体积的计算方法,再让学生通过想象将计算方法由具体图形推导至一般图形,并借此得到一般化的图形公式。这样的过程不仅能够让学生理解图形公式背后的数学道理,而且可以发展学生的空间观念。
在教学苏教版小学《数学》六年级上册“长方体和正方体的体积”一课时,笔者为学生提供了若干个1立方厘米的小正方体,先让学生用这些小正方体搭一个长、宽、高分别是4厘米、3厘米、2厘米的长方体,再让学生根据搭的过程说说这个长方体的体积为什么可以用4×3×2来计算。接着,让学生将这个长方体的高变为3厘米,长和宽不变,并让学生说说现在这个长方体的体积怎么计算,以及为什么可以这样计算。随后,让学生想象:“如果这个长方体的长和宽不变,将高逐渐变为4厘米、5厘米……这个长方体的体积可以怎么计算,为什么可以这样计算?”学生根据想象能够归纳出:当长方体的长、宽、高分别是4厘米、3厘米、a厘米时,可以用4×3×a来计算它的体积。随后,笔者让学生用同样的方法想象,仅当长或宽发生变化时,长方体的体积可以怎么计算,以及为什么可以这样计算。最后,学生在三次想象的基础上,归纳出长方体的体积公式V=abh。
让学生依据一个具体的长方体的体积计算方法,通过控制变量的方法,依据想象逐步得出在长和宽不变、或宽和高不变、或长和高不变的情况下,长方体的体积如何计算,以及为什么可以这样计算,最后归纳出长方体的体积公式。在这样的教学过程中,学生不仅通过探究得到了长方体的体积公式,而且深刻理解了体积公式背后的数学道理,空间观念也在想象中得到了有效的培养。经常这样教学,会让学生在获得公式的过程中,在脑中形成图、式转化过程的表象,成为空间想象的支柱。
(二)在公式应用过程中,让学生通过想象发展空间观念
在图形公式的教学中,不少教师仅仅将应用公式的教学目标定位为帮助学生进一步理解公式、形成技能,而忽视了空间观念的培养。其实,在应用公式时,尤其是在初始阶段,不仅要让学生进一步理解公式、形成技能,而且可以让学生通过想象发展空间观念。
在教学苏教版小学《数学》三年级下册“长方形和正方形的面积”一课时,一名教师在练习中出示这样的问题:“一个长方形的面积是24平方厘米,你能想象出它是什么样子吗?请在方格纸中画出来(每个小方格面积是1平方厘米)。”面对这样的问题,有些学生想到这个长方形是由24个1平方厘米的小正方形组成的,这24个小正方形可能排成1排,也可能排成2排、3排或4排,从而画出4个不同的长方形。也有学生逆向运用长方形的面积公式想到这个长方形的长和宽可能是24厘米和1厘米、或12厘米和2厘米、或8厘米和3厘米、或6厘米和4厘米,也画出了4个不同的长方形。
在上述练习中,问题由封闭变为开放,解决问题的思路由顺向变为逆向,学生在解决这个问题时,不是简单地运用面积公式计算长方形的面积,而是借助小正方形、或逆向运用公式在头脑中想象出多种不同形状的长方形,再将想象出的长方形在方格纸中画出来。这样的练习不仅帮助学生进一步巩固了对长方形面积公式的理解,而且发展了学生的空间观念。
二、不可忽视数学思想的感悟
数学思想是数学核心素养的重要组成部分,让学生在学习数学的过程中感悟数学思想是数学教学的重要目标。数学思想蕴含在数学知识形成、发展和应用的过程中,是数学知识和方法在更高层次上的抽象和概括。图形公式教学中蕴含着丰富的数学思想,需要我们深入挖掘,并让学生感悟。
(一)让学生经历过程感悟数学思想
数学思想蕴含在数学知识形成、发展和应用的过程中,想要让学生感悟数学思想,就需要让学生充分经历数学知识的形成、发展和应用的过程。在图形公式教学中,我们要让学生充分经历图形公式的形成过程,从而让学生感悟蕴含在其中的数学思想。
在教学苏教版小学《数学》五年级上册“三角形的面积”一课时,教师先出示图1方格图中的三个三角形,让学生说说它们分别是什么三角形,再让学生说说想先研究谁的面积,多数学生依据直觉想要先研究直角三角形的面积。在研究直角三角形的面积时,有学生用数格子的方法直接数出直角三角形的面积,还有的学生想到用两个一样的直角三角形拼成一个长方形或平行四边形,或将直角三角形等积转化成长方形或平行四边形,并依据转化前后图形之间的关系算出直角三角形的面积,从而得到直角三角形的面积计算方法。随后,教师让学生利用研究直角三角形的面积时获得的经验,研究锐角三角形和钝角三角形的面积计算方法。教师带领学生在前面分类研究的基础上,归纳出三角形的面积公式。最后,教师引领学生回顾获得公式的过程,让学生感悟蕴含在其中的分类、归纳思想。

图1
上述教学过程中,学生充分经历了先分类探究、再归纳公式的数学活动过程,从中不仅获得了三角形的面积公式,而且感悟到分类、归纳的数学思想。在教学过程中,教师要善于利用每个小环节,让学生感悟其中所蕴含的某种数学思想,这也是一种不可或缺的过程感悟和经验积累。
(二)让学生通过对比感悟数学思想
对比是感悟数学思想的最有效策略之一,通过对比能够让学生体会数学思想的价值,从而加深对数学思想的感悟。在图形公式教学中,我们可以让学生通过对比,感悟蕴含在图形公式中的数学思想。
在教学苏教版小学《数学》五年级上册“平行四边形的面积”一课时,笔者先出示一个方格图中的平行四边形让学生求其面积(每个小方格面积是1平方厘米)。有学生想到用数方格的方法数出面积,有的学生想到将平行四边形沿一条高分成一个直角梯形和一个直角三角形或两个直角梯形,再将它们拼成一个长方形,算出原来平行四边形的面积。这两类方法中,前一类方法是直接测量法,较为繁琐;而后一类方法运用了转化思想,是间接测量法,较为简单,且能根据其推导出平行四边形的面积公式。在学生运用不同的方法求出平行四边形的面积后,教师让学生对比这两类方法,学生从中感悟“转化能够化繁为简,能够在未知和已知之间建立联系”。
上述教学过程中,学生不仅通过探究自主发现了平行四边形的面积计算方法,而且在对比中体会到转化思想的价值,从而对转化思想形成较为深刻的感悟。
图形公式教学中不仅蕴含着转化思想、分类思想,还有其他的数学思想,如推理思想、模型思想、符号化思想等,这些数学思想都需要教师在教学中有意识地、循序渐进地运用合适的方法让学生去感悟。
三、不可忽视活动经验的积累
数学活动经验的积累是数学素养提高的重要标志,是学生不断经历、体验各种数学活动过程的结果,帮助学生积累数学活动经验是数学教学的重要目标。数学活动经验需要在“做”和“思考”的过程中积淀,是在数学学习过程中逐步积累的。在图形公式教学中,我们可以让学生充分经历“做”和“思考”的过程,从而帮助学生积累数学活动经验。
(一)让学生在“做”的过程中积累数学活动经验
数学活动经验是在“做”的过程中逐渐积累起来的,“剪一剪”“拼一拼”“做一做”等操作活动都能丰富学生的数学活动经验。在图形公式教学中,我们可以设计多样的、有层次的操作活动,帮助学生积累数学活动经验。
在教学苏教版小学《数学》三年级下册“长方形的面积”一课时,教师为学生提供6个1平方厘米的小正方形,让学生依次测量三个长方形的面积,三个长方形的长、宽分别为3厘米和2厘米、5厘米和2厘米、10厘米和8厘米(如图2所示)。在测量第一个长方形面积时,多数学生用这6个小正方形将其铺满,从而得到它的面积。在测量第二个长方形时,由于提供的小正方形不够用了,有学生想到了与同桌合作的方式,将两个人的小正方形聚在一起,通过铺满的方式得到这个长方形的面积;有的学生通过铺长和宽的方式,根据想象铺满得出这个长方形的面积。在测量第三个长方形的面积时,由于6个小正方形不能铺满它的长或宽,所以很多学生束手无策。经过一段时间的思考后,有学生想到了用小正方形的边长测量大长方形的长和宽,最终根据长和宽想象出铺满这个长方形需要多少个小正方形,从而得出这个长方形的面积。
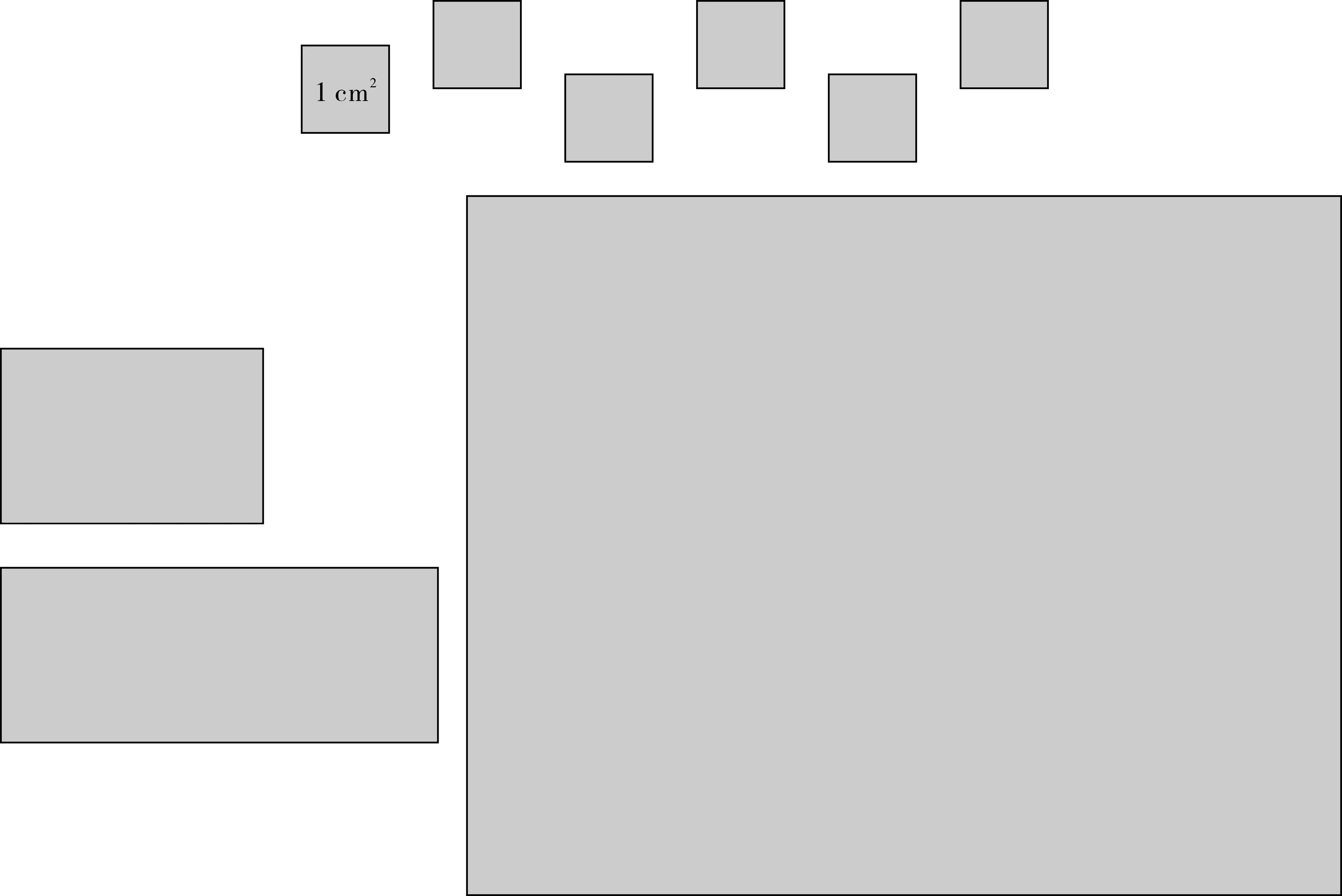
图2
在上述教学过程中,通过学生先用铺满的方法得出长方形的面积;再铺长方形的长和宽想象出长方形的面积;最后利用小正方形的边长测量出长方形的长和宽,再根据测量的结果想象出铺满的结果,得出长方形的面积。学生从直接测量逐步过渡到间接测量,从直接动手操作逐步过渡到在头脑中操作,其数学活动经验得到了充分的积累。
(二)让学生在“思考”的过程中积累数学活动经验
学生的数学活动经验不能止于操作经验,而需要通过反思、抽象、概括等思维活动,内化为学生的思维经验。在图形公式教学中,我们可以设计符合学生实际的、有效的思维活动,帮助学生积累数学活动经验。
在教学苏教版小学《数学》六年级上册“长方体和正方体的体积”一课时,教师在提出探究任务(测量一个长方体木块的体积)后,出示三个测量工具让学生选择(如图3所示),多数学生选择用小正方体测量,其理由是测量体积时要用单位体积。此时,教师并未让学生直接去测量,而是让学生思考前两个工具可以测量什么、怎么测量,学生通过思考激活了长度、面积的测量经验,以及长方形的面积公式的推导过程。然后,学生借助长方形面积公式的探究经验,通过探究得出了长方体的体积公式。教师让学生思考“前两个工具能否测量出长方体的体积”,学生通过思考明确前两种测量工具都可以测量出长方体的长、宽、高,也能通过计算得出长方体的体积。此刻学生也明白了,因为长方体木块是实心的,不能通过往里面填充小正方体测量它的体积,所以并不能直接用小正方体测量长方体的体积,而只能利用小正方体棱长的长度去测量大正方体的长、宽、高而已,这与用其他两个工具测量在本质上是一样的。最后,教师让学生对上述探究过程进行反思,通过反思,学生不仅感悟到不同维度的测量原理及本质之间的相似性,而且明白了直接测量和间接测量之间的联系,以及从直接测量走向间接测量的必要性。
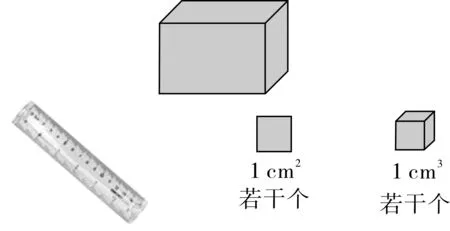
图3
在上述教学过程中,通过让学生选择测量工具,帮助学生在一维、二维和三维之间建立联系,启迪学生将长方形的面积公式探究经验用于长方体的体积公式的探究过程中。学生从中获得的数学活动经验不仅仅是操作经验,还有思维经验,并且这种数学活动经验可以迁移到其他类别的测量中,是一种可生长的数学活动经验。
