基于正态模型的电气试验方法优化及参数估计分析
2021-12-14鲁聪张亮张源张亚龙
鲁聪 张亮 张源 张亚龙
(1、国网宁夏电力有限公司检修公司,宁夏银川 7500112、宁夏中科恒瑞智能科技有限公司,宁夏银川 750011)
正态分布是一种统计学领域用于描述概率分布特性的概念,在社会生产与日常生活中常使用统计学方法进行正态分布参数的估算,通过获取标准偏差、中值等参数的估计值,获取到研究对象的正态特征。当前在电力科研与生产领域常开展放电特性试验,并根据试验结果掌握放电电压的具体数值,为输电线路及电力设备空气绝缘间隙的科学设计提供借鉴思路。通过选取不同方法进行统计分析与比较,能够为实际工程设计环节可靠性提升以及试验参数统计方面的理论研究提供现实借鉴意义。
1 空气间隙放电特性试验
1.1 试验方法
通常在过电压在情况下的空气间隙大小、绝缘子片数量将直接影响到变电站电气设备及输电运行的效能与稳定性,当前主要通过开展放电特性试验,从中提炼出放电电压值与偏差值,由此实现对空气间隙、绝缘水平等指标的科学配置[1]。在试验方法设计上,选取冲击电压发生器作为试验装置(如图1 所示),通过对棒电极、板电极之间的电气间隙处施加脉冲电压,即可开展数次放电试验。考虑到单次试验之间存在1~2min 的时间间隔,因此可确认各放电试验无显著相关性、属于独立事件,符合正态分布。当前在输电线路、变电站的绝缘配合设计上,主要基于50%放电电压值与空气间隙距离的差值进行距离计算,运用放电电压的标准偏差计算结果生成绝缘配合系数,但如何保证参数估计结果的精确性,成为电气试验中亟待解决的重点问题。在参数估计上,主要运用多级法或升降法进行试验结果的统计分析,获取50%放电电压值U50及标准偏差值σ 等统计参数,然而不同试验方法获取到的统计结果存在一定差异,还需结合具体试验数据进行比较分析。

图1 冲击电压发生器
以某棒-板电极装置为例(装置结构如图2 所示),该装置在长15m、直径60mm 的钢棒端部安装一个直径为60mm 的半球作为棒电极,选取规格为20×20m 的钢板接地后作为板电极,两电极之间设有5m 的空气间隙。待完成试验装置准备后,使板电极处于地电位,将棒电极顶端与高压引线连接,基于IEC标准对其施加250/2500 的标准操作冲击电压,并结合试验环境温湿度、大气压力等指标进行试验结果的修正。根据以往电气试验结果进行施加电压数值与放电几率之间关系的研究,可发现二者符合正态分布规律(如图3 所示),可通过建立正态模型计算出试验数据、完成参数估算[2]。
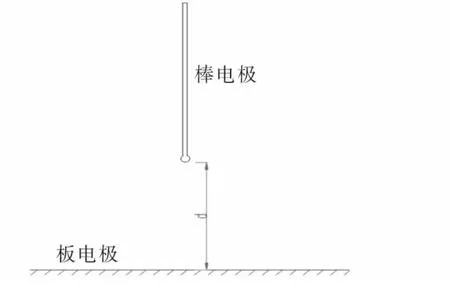
图2 某棒-板电极装置示意图

图3 正态分布曲线
1.2 试验操作与结果
1.2.1 多级法放电试验
在试验操作环节,首先选定m 个不同等级的电压(本次试验中m 取值为5)设为Ui(i=1,2,……,m);其次针对各级电压分别开展ni次加压试验(本次试验中ni取值为13),通过试验获取到电压幅值、判断有无放电情况,并记录试验数据;最后运用数理统计方法计算出U50和σ 等数值。
通过观察试验数据的统计结果可知,针对5 个不同级别电压分别开展13 次放电试验,对5 个电压等级分别施加1205kV、1277kV、1385kV、1397kV 和1456kV 的电压,获取到与之对应的放电比率值fi分别为0.078、0.386、0.463、0.693 以及0.924。从中可以看出,当施加电压值由1205kV 增加至1456kV 后,放电比率的均值由7.8%提升至92.4%,由此计算出正态分布统计中值,即为本次试验中所需计算的U50和σ。
1.2.2 升降法放电试验
在试验操作环节,同样将电压等级设定为Ui,对其施加n 组电压,并且对各组分别开展m 次加压试验,在每一次加压试验环节均需参考上一级电压的试验结果进行极差ΔU 增减量的调节。在试验程序设计上,针对放电比率的最小值、最大值两种情况寻求与之匹配的电压水平,分别建立以下两种程序:(1)耐受程序,假设对Ui施加一组m 次加压,倘若在此过程中未出现破坏性放电,可增加一个极差ΔU;当发生破坏性放电现象时,则减少一个ΔU。(2)放电程序,假设对Ui施加一组m 次加压,当耐受次数≧1 次时,可增加一个ΔU;当耐受次数<1 时,需减少一个ΔU。
本次试验将m 取值为1,基于两种程序分别开展15 次放电试验,将单次试验对应的电压值数据进行汇总,从中可归纳出1186 ~1190kV、1230 ~1294kV、1309 ~1381kV、1405 ~1407kV共计4 种电压等级。观察试验数据的统计分析结果可知,依据4种电压等级的分布区间获取对应的施加电压均值1187kV、1259kV、1333kV 和1406kV,试验次数分别为1 次、14 次、11 次和4 次,各级电压对应的放电比率依次为0、0.07、0.545 和1。从中可以看出,由于第1、4 级电压试验获取到的放电概率分别为0 和100%,不符合正态分布规律、属于无效数据,因此仅将剩余两级试验数据保留,为后续参数估计提供数据支持。
2 基于最小二乘法的参数估计结果比较
2.1 最小二乘法的计算


2.2 不同试验方法的参数估计结果
2.2.1 多级法参数估计

2.2.2 升降法参数估计

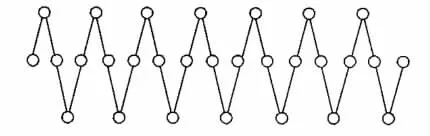
图4 理想化升降法示意图
2.3 参数估计结果比较
将运用两种试验方法获得的参数估计结果进行比较,如表1所示。从中可以看出,两种试验方法获取到的放电电压估计值存在极小差距,其参数估计结果基本保持一致;但标准偏差的差异值为42.59%,说明两种方法的估计结果存在明显差异。通过对产生差异的原因进行分析可知,基于最小二乘法原理运用升降法进行试验设计,分别对各级电压施加以ΔU 为单位的增减量产生数值变化,但各级电压变化量的差别可控制在一定范围内,以Uˆ50数值为基准略微波动,而排除最低电压、最高电压对应的两种概率极端值情况后,可将概率点控制在3 个以内,其概率值整体围绕50%浮动,并且不考虑0~15.6%、84.6%~100%两个区间内的概率值,不符合正态分布规律,计算出的标准偏差估计值较真实值仍存在显著差距,无法为实际工程设计环节提供可靠指导。
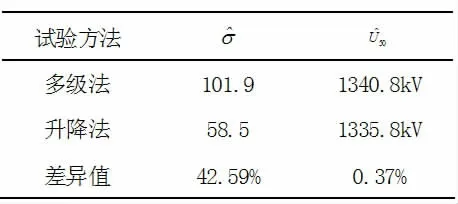
表1 参数估计结果比较
当前在通用试验操作领域普遍采用多级法进行σˆ的求解,运用该方法获取到的统计结果具备良好的稳定性,且参数估计值的置信检验结果较为理想,将该方法应用于电极装置空气间隙试验中,能够有效适应放电分散度差距较大情况下的间隙试验需求,在实际操作环节简单、易操作,满足空气间隙、绝缘匹配等试验的统计分析要求,具备良好适用性能[3]。但在实际工程设计环节仍需注意禁止直接运用标准偏差的统计结果进行电气绝缘设计,防止造成绝缘尺寸偏小的问题,处理好标准偏差参数估计结果与真实值间的关系,并采取有效纠偏措施,为工程设计工作实践提供参考价值。
3 结论
总体来看,通过运用多级法、升降法对某棒-板电极装置进行放电试验,获取到一定空气间隙下的放电概率分布特征。试验结果表明,两种方法在计算50%放电电压估计值的计算上均具备较高准确度,但升降法求解标准偏差估计值时仍存在明显差异,因此在工程设计实践中推荐采用多级法进行标准偏差求解,为绝缘配合水平与空气间隙等指标的科学配置提供有效方法,最大限度规避设计缺陷、提高电气设计水平。
