区域不同土层土壤容重建模方法比较
2021-12-14吴思聪陈弘扬庄红娟周鹏飞张世文
方 兵,吴思聪,陈弘扬,宋 强,庄红娟,周鹏飞,杨 斌,张世文*
(1.安徽理工大学地球与环境学院,安徽 淮南 232001;2.中国科学院南京土壤研究所,江苏 南京 210000;3.安徽理工大学空间信息与测绘工程学院,安徽 淮南 232001)
【研究意义】土壤容重(bulk density,BD)作为土壤物理性质之一,对于评估土壤养分、区域碳储量、土壤紧实度和土壤水分运移等至关重要[1],被广泛作为各种预测和描述性土壤模型的输入参数。尽管土壤容重数据十分重要,但在实际的获取工作中,常常由于土壤中植物根系和砾石较多等原因,很难或无法通过环刀法采样来测定[2];此外,由于环刀法操作繁琐,在野外大量获取容重数据是一件费时费力、甚至不切实际的工作[3]。因此在土壤科学领域,一些国内外学者开始利用日常易测定的土壤理化性质对土壤容重等不易测定的理化性质进行模拟,这种更易获取和实现的数学模拟方法被统称为土壤转换函数(pedotransfer functions,PTFs)。【前人研究进展】国内外用于构建土壤转换函数模型的方法众多,从基本统计方法到多变量空间统计均有涉及。采用逐步回归确定转换函数模型,并使用验证集法(以均方根误差RMSE作为误差度量指标)对模型测试误差进行估计是最常被使用的建模流程[3-5]。如WANG等[5]在中国黄土高原地区,从1254个土壤样品中随机抽取1003个土样作为模型训练集使用逐步多元回归得到转换函数模型,再将余下的251个土样作为测试集,以RMSE作为误差度量指标来评价模型的优劣。但逐步回归因追寻高效的运算效率从而无法保证在全部的变量组合模型中得到最优变量组合;同时,用以评判模型优劣的验证集法,对数据训练集和测试集的分割存在随机性,使模型测试误差的估计波动较大,往往高估了模型的预测能力,进而降低了模型的普适性与预测精度。近年来许多学者引入了神经网络的方法来提升模型输出的稳健性与预测精度,如高如泰等[6]基于BP-神经网络(BP-ANN)以土壤粒径分布、土壤容重、土壤有机质等土壤基本理化性质来对土壤水力学参数进行预测并得到较好的结果。廖凯华等[7]利用主成分分析(PCA)与神经网络相结合的方法(PANN),利用PANN消除了ANN输入层参数的相关性,降低了网络的拓扑复杂度,从而使模型的预测能力得到提升。神经网络虽在土壤变量预测上提高了模型输出的稳健性与预测精度,但该方法不能有效刻画出土壤转换函数的具体形式,进而影响了其在实践中的应用与推广。【本研究切入点】针对当前各种建模方法的不足,本文采用融合十折交叉检验的最优子集和lasso压缩估计的方法,选取影响土壤容重(BD,mg/m3)变化的环境因子,包括土壤有机质(SOM,g/kg)、砂粒(Sand,%)、黏粒(Clay,%)和粉粒(Silt,%)的体积分数、土壤含水量(WC,%)与土壤采样深度(Depth,cm)作为预测变量,分不同垂直尺度(0~10、10~20、20~40、0~40 cm)对皖北平原上的土壤容重进行模拟,并与现有土壤容重转换函数进行精度比较,同时探讨了最优子集和lasso压缩估计在不同垂直尺度下的适用范围。【拟解决的关键问题】本研究通过探讨不同建模方法的优劣,选取最优建模方法,以期为类似区域的土壤容重研究提供方法支撑。
1 材料与方法
1.1 研究区概括与数据处理
研究区位于安徽省北部(图1),属于皖北平原区域,全境属暖温带半湿润季风气候,并具有以暖温带向北亚热带渐变的过渡带气候特征。研究区北部与黄河决口扇形地相连,南部与江淮丘岗区隔淮河相望,大部属平原地带,地势平坦,总面积达3.9万km2。皖北平原年降雨量820~950 mm,境内河流均属淮河水系。土壤类型以砂姜黑土为主,并包含少量潮土,土层厚度在100~120 cm。
为建立区域容重转换模型,对研究区利用网格布点与分层抽样相结合的方法进行土壤样品的分层(0~10、10~20、20~30和30~40 cm)采集工作。采样时每个样点随机设置3个重复,共设采集样点34个,土样816个,其中环刀土样和混合土样各408个。土壤容重与土壤含水量采用环刀法测定,105 ℃下烘至恒重后,称重计算;土壤有机质采用重铬酸钾—外加热法测定;土壤机械组成采用比重计法,依据土壤矿质颗粒粒径分级标准(美国制):砂粒(2.000~0.050 mm),粉粒(0.050~0.002 mm),黏粒(<0.002 mm)[8]。
1.2 研究方法
1.2.1 十折交叉检验 十折交叉验证(Ten-fold cross-validation)是对一种统计学方法测试误差的估计。本文中,交叉验证法被用来评价最优子集法中不同变量规模下的模型表现能力,以及为lasso压缩估计的调节参数Lambda选择一个合适的值,用来均衡模型的方差—偏差,提升模型的稳健性。
十折交叉方法的具体实施过程,将土壤样品的数据集随机等分成10份,轮流将其中的9份用于训练数据集,剩下的1份作为检验数据集,并用残差平方和(residual sum of squares,RSS)与均方根误差(root mean squared error,RMSE)作为不同模型下的评价指标。
(1)
(2)
1.2.2 最优子集法 最优子集法(optimal subset method)对研究区p个土壤属性:土壤有机碳、土壤砂粒、黏粒和粉粒的体积分数、土壤含水量和土壤采样深度作为预测变量的所有可能组合,进行拟合回归。该算法对含有一个预测变量的模型(p|1),拟合p个模型,并以RSS最小作为(p|1)的最优模型;对含有两个预测变量的模型(p|2),拟合p(p-1)/2个模型,同时也是以RSS最小为依据,选取(p|2)的最优模型,依次类推,最终在这p个模型中,以十折交叉验证法(RSS作为度量指标),选取一个测试误差最低的模型作为最优模型。
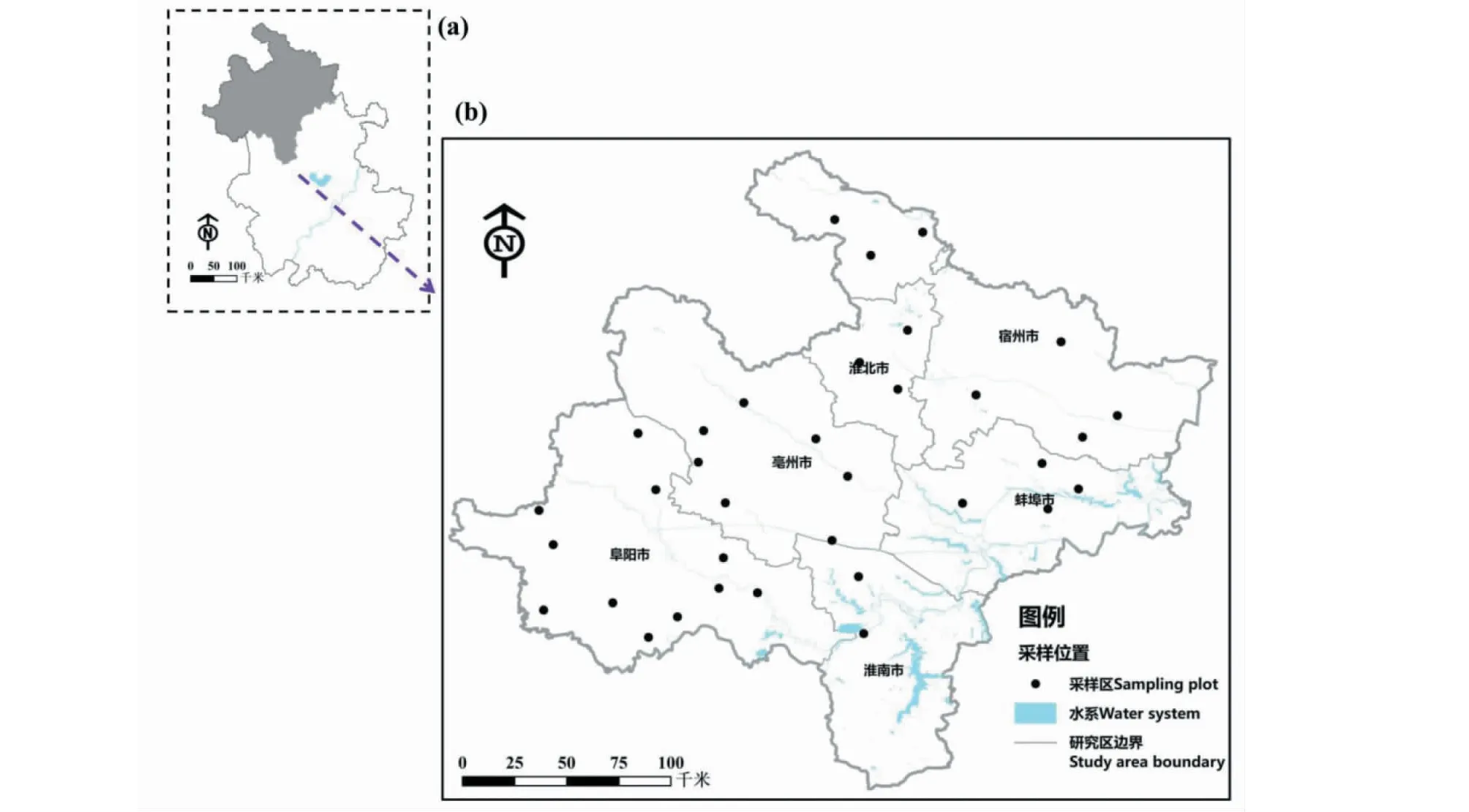
图1 研究区位置与采样点分布Fig.1 Location of the study area and distribution of sampling points
为了提高土壤容重转换函数模型的精度,本文引入最优子集法得到最优的p个模型,并采用十折交叉验证规避了训练集和验证集在分割上存在随机性,以残差平方和RSS作为度量指标,评价这p个模型的表现能力,并找出预测精度较高,模型变量组合最优的土壤容重转换函数模型。
1.2.3 lasso压缩估计法 在土壤容重转换函数模型的研究中,简单线性拟合、多元逐步回归法都是基于最小二乘法得以实现,该方法通常保证了所选数据训练集的偏差值较小,但无法降低模型方差的大小,即模型对于给定数值的输出稳定性较差。为了克服最小二乘法的缺陷,国内外学者引入了BP神经网络的方法来提升模型的稳健性[3,9-10],虽在土壤变量预测时提高了模型的稳健性与预测精度,但该方法并不能有效刻画出土壤转换函数的具体形式,进而影响了其在实践中的应用与推广。综上,本文引入lasso回归,以牺牲小部分模型偏差为代价,从而提高模型的稳健性,并给出具体的模型刻画形式。
与最小二乘法不同,lasso法并不具有尺度不变性,所以需要事先对训练集数据进行标准化处理,如下式:
(3)

lasso回归系数估计值通过最小化下式得到:
(4)

1.2.4 数据处理 土壤理化性质的描述性统计、Pearson相关分析、LSD多重比较以及基于融合十折交叉检验的最优子集法、lasso压缩估计法的模型构建及其相关图片的制作均使用R-3.5.3平台进行。
2 结果与分析
2.1 土壤理化性质的统计特征
2.1.1 描述性统计 土壤容重含量介于1.33~1.72 mg/m3(表1);土壤有机质介于1.28~44.62 g/kg,土壤含水量介于9.12%~35.10%,砂粒含量介于18.92%~84.83%,粉粒含量介于13.42%~74.27%,黏粒含量介于0.67%~12.59%。在土层0~40 cm下,土壤容重与其它土壤理化性质相比(如:土壤有机质、土壤黏粒),其变异系数最小,处于低变异水平(CV=0.08%);土壤含水量、粉粒和黏粒所选数据达到中等变异水平(CV=19.10%、24.13%和28.43%),土壤有机质与黏粒数据达到高度变异水平(CV=37.90%、52.96%)。土壤有机质、黏粒含量处于高度变异水平可能与研究区内各采样小区上所从事的不同农业活动有关[11-12]。

表1 土壤理化性质的描述性统计(n=134)
集中趋势和离散趋势是数据分布的2个重要特征,峰度(skewness)与偏态(kurtosis)可以通过描述数据分布形状的对称性、偏斜程度以及扁平程度反应这些分布特征,并度量所选数据分布与正态分布的差异。所选土壤容重数据服从正态分布,其频数分布图显示出轻微左偏和平顶(Skew.=-0.04,Kur.=-0.48);其它土壤理化性质数据也都较好地服从正态分布(表2)。
2.1.2 垂直变化规律 土壤有机质的含量在表层达到最大值(图2),并随土层厚度的增加而降低,其含量为20.86、15.63、11.82和9.90 g/kg,土壤容重呈现出先上升后降低的趋势,并在土层深度20 cm处达到最大值,为1.48、1.56、1.54和1.52 mg/m3。有研究表明,土壤容重与土壤有机质在土壤表层呈极显著负相关关系,即随着土层厚度的增加,土壤有机质含量的逐渐减少,土壤容重则呈现出增大的趋势[13]。土壤含水量与容重的变化趋势呈现出相反的变化,即先降低后升高,22.81%、20.19%、21.09%与22.60%;所选土壤黏粒、粉粒与砂粒的含量的变化趋势较为平稳,均在10%的幅度内波动(5.42%~6.29%、47.34%~48.92%和44.98%~47.28%)。综上,土壤有机质、土壤含水量、土壤容重的含量在表层0~20 cm变化较大,在土层20~40 cm变化较小,因此在后续研究中将垂直尺度划分为0~10、10~20、20~40与0~40 cm。

图2 土壤理化性质的垂直变化规律Fig.2 Vertical variation of soil physical and chemical properties

BD.土壤容重(mg/m3);WC.土壤含水量(%);SOM.土壤有机质(g/kg);Silt.粉粒(%);Sand.砂粒(%);Clay.黏粒(%) BD.Soil bulk density(mg/m3);WC.Soil water content(%);SOM.Soil organic matter(g/kg);Silt.Silt(%);Sand.Sand(%);Clay.Clay(%)图3 土壤属性与所选容重之间的相关系数Fig.3 Correlation coefficient between soil properties and selected bulk density
2.1.3 土壤容重的相关性分析 Curtis、Aleaxander与Benmoux等[3,14-16]认为土壤有机质、土壤质地是影响土壤容重变化的重要环境因子;土壤含水量在Suuster等[17]开发的预测模型中具有显著的统计学意义,并与容重呈反比;Qiao等[18]在构建转换函数模型时证明了土壤采样深度在对容重变异性的解释占据重要作用。根据现有研究,本文选取了上述与土壤容重相关的土壤属性,对所获得的土壤样本分不同垂直尺度进行了Pearson相关性分析(土壤采样深度为离散性变量,不参与相关性分析,图3)。
从图3-a的下三角矩阵中看出,土壤容重与其它土壤各属性的散点分布呈现出较高的非线性关系;上三角矩阵显示各土壤属性之间的Pearson线性相关系数,其中土壤容重与土壤有机质呈现出显著的负相关性水平(corr.=-0.17*),这与王霖娇等[16]的研究结果一致,Yun qiang W[23]指出土壤有机质含量可以解释土壤容重81.00%的变异性,是改变土壤空隙结构的重要聚合体,同时具有较强的吸水性,有机质含量的增加直接影响了土壤容重的下降[27];容重与其它土壤属性的相关系数介于-0.07~0.20,均处于较低的线性相关性,与下三角矩阵所得结论相一致。
从图3-b可知,0~10 cm土层中,土壤容重与土壤有机质呈现出显著正相关线性关系(corr.=0.33*),其系数的绝对值较其它土壤属性相比达到最高;20~40 cm土层中,土壤容重与黏粒呈现出显著的弱线性关系(corr.=-0.25*);0~40 cm土层中,土壤容重与土壤有机质和土壤含水量呈现显著的弱线性关系(corr.=-0.17*,-0.20*)。
Yang[13]指出土壤容重与土壤其他属性间可能存在显著的非线性关系。为使研究区土壤容重的预测精度得到提高,在后续模型的构建中,将会对现有数据中的一些土壤预测变量进行4种常见的转换,如:lnSOM、SOM2、(lnSOM)2和1/SOM。
2.2 模型的建立及其精度比较
2.2.1 土壤容重的最优子集回归模型 由图4可知,土层厚度为0~10和10~20 cm时,当变量数个数为1时(分别为:1/SOM、ln(SOM)),模型残差平方和值(RSS=0.005、0.002)达到最低。土层厚度为20~40 cm时,当所选3个变量(SOM、WC和Sand)时,残差平方和(RSS=0.005)达到最低。土层厚度为0~40 cm时,其所选2个变量[ln(SOM)、lnWC]使模型普适性达到最佳(RSS=0.006)。
4种函数模型精度均较高(RMSE接近0,图5),从散点分布趋势来看,土层0~10、10~20和20~40 cm,容重预测值与实际值较为接近1∶1轴,即预测结果较好,但土层0~40 cm,容重预测值与实际值偏离1∶1轴较大;从土壤容重转换函数的变量形式来看,易小波等[28]利用状态空间方程估算土壤容重值时提出,不同土层深度下土壤容重的影响因素不同,在本文得以印证。土层0~20 cm时土壤有机质是其主要的影响因素;而土层20~40 cm时,土壤有机质、含水量和砂粒是其共同影响因素。土壤有机碳含量随土层厚度的加深而逐渐减小,也是影响函数模型参数的重要因素,在土壤有机质含量较高的土壤中,容重主要受有机质含量影响较大,而在有机质含量较低时,土壤质地等其它理化性质才对容重产生影响[4,19-20]。

土层厚度:(a).0~10 cm;(b).10~20 cm;(c).0~40 cm;(d).20~40 cm Soil thickness:(a).0-10 cm;(b).10-20 cm;(c).0-40 cm;(d).20-40 cm图4 不同土层深度下的十折交叉验证结果Fig.4 Ten-fold cross-validation results for different soil depths

图5 基于最优子集法的土壤容重预测值与实测值比较Fig.5 Comparison of predicted values of soil bulk density and measured values based on optimal subset method
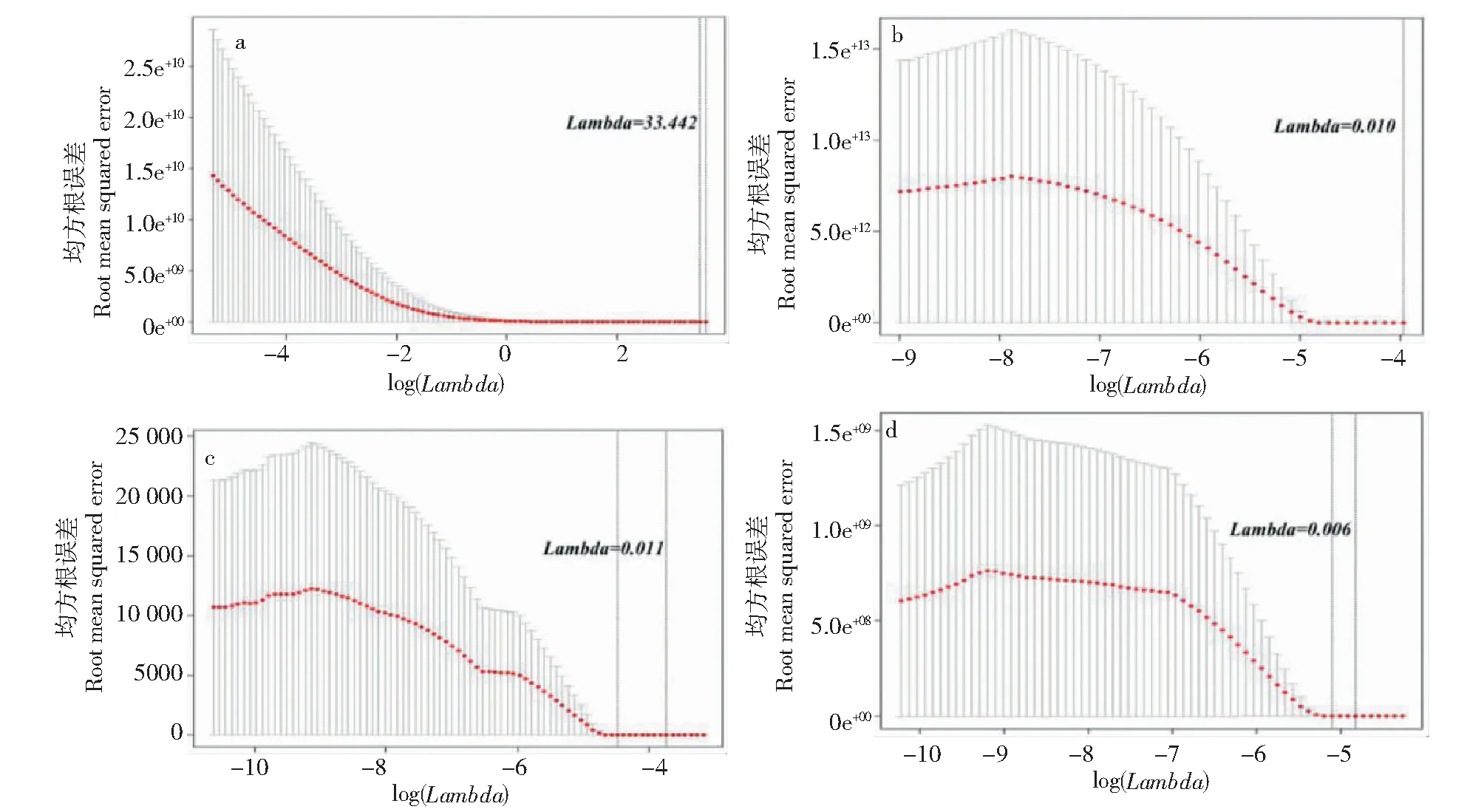
土层厚度:(a).0~10 cm;(b).10~20cm;(c).0~40 cm;(d).20~40 cm Soil thickness:(a).0-10 cm;(b).10~20cm;(c).0~40 cm;(d).20~40 cm图6 基于十折交叉验证的Lambda最优选择Fig.6 Lambda optimal selection based on ten-fold cross-validation
2.2.2 土壤容重的lasso压缩估计模型 Lambda值选择在-102~1010的范围进行土壤转换函数形式的压缩估计,该范围包含了只含截距项的空模型到最小二乘估计的拟合模型的所有情况,并利用十折交叉检验法计算每个值的交叉验证误差,以RMSE作为评价指标,选择误差最小的值。在土层厚度0~10、10~20、20~40和0~40 cm下最优的Lambda=33.442、0.010、0.011和0.006(图6);除土层0~10 cm的Lambda对回归系数估计的影响程度较大,对其余值的影响都较小。
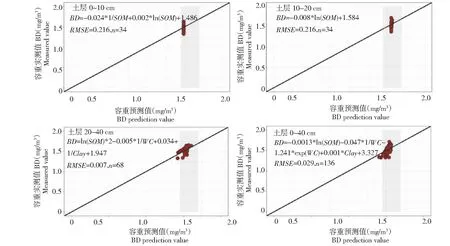
图7 基于lasso压缩估计法的土壤容重预测值与实测值比较Fig.7 Comparison of soil bulk density predictions and measured values based on lasso compression estimates
将上述所得Lambda的最优值带入lasso模型进行各土层下的转换函数模型的建立(图7)。lasso模型在土层0~10与10~20 cm下的土壤容重的预测精度较低,RMSE分别为0.216、0.091 mg/m3,较最优子集法相比分别下降了67%和40%;从散点分布趋势可以看出,容重预测值的变化范围较小(1.485~1.487、1.553~1.572 mg/m3),与土层的容重实际值的分布偏离较大。土层20~40与0~40 cm下的土壤容重预测精度(RMSE=0.007、0.029 mg/m3)较最优子集法相比得到了较大的提升,分别为90%和53%;从散点分布趋势来看,散点整体趋势较最优子集法相比,更加倾向于1∶1轴,即土壤容重预测值与实际值偏离较小,特别是在土层20~40 cm偏离达到最低。
2.2.3 两种土壤容重转换函数预测精度的比较分析 对于土壤容重的实际值、最优子集法与lasso法所得土壤容重预测值进行描述性统计与LSD多重比较(表2)。
由土壤容重的最大值、最小值以及变异系数可知,在土层0~10、10~20 cm,lasso法预测所得最大值偏低,最小值偏高,变异系数较低,由此说明lasso法在模拟土壤容重时表现出一定的平滑效应,而在土层20~40、0~40 cm下,最优子集法较lasso法相比平滑效应更为明显;LSD多重比较显示两种方法所得土壤容重预测值之间不存在显著性的差异,其与土壤容重的实际值也不存在差异(P>0.05),从统计学角度来看,上述2种方法对于土壤容重的预测值与实际值在数值上相差不大,即均为正确的土壤容重预测值。但综合平均值和标准差,土层0~10、10~20 cm,最优子集法较lasso法预测效果更佳,土层20~40、0~40 cm,lasso法预测值则更为接近实际土壤容重的分布趋势。综上,土层0~10,10~20 cm,使用最优子集法较lasso法效果更好;土层20~40、0~40 cm,使用lasso法模拟土壤容重更为精确。
2.2.4 不同土壤容重转换函数在皖北平原表现能力比较 由于成土过程、气候、生物、母质以及人类活动等影响,使土壤自身存在广泛的空间异质性的特点,所以土壤转换函数具有一定的研究区和适用限制范围;韩光中等[3]曾对中国的主要土壤类型分别建立了最适宜的土壤转换函数,结果显示不同土壤类型所具有的转换函数在形式上与变量上均存在较大差异。本文从现已发表的国内外土壤容重转换函数模型中,以存在土壤有机质、土壤质地、土壤含水量和土壤采样深度为参数的选取依据,结合本文已有土壤数据集,按照相应条件代入各传递函数模型中,求得土壤容重的预测值,并以均方根误差(RMSE)与平均误差(ME)为评价指标来衡量在皖北平原区域上土壤容重预测的适用性潜力。

表2 2种方法下的土壤容重数据的统计分析
由表3可知,各土壤转换函数在研究区的适用性表现不一。从平均误差值来看,利用Curtis R O(1964)、Adams W A(1973)和Benites V M(2007)模拟得到的ME值为正,说明这些容重传递函数模型高估了容重值;其余函数模型的ME值均为负值,说明了函数模型低估了容重值。通过RMSE作为另一个评价指标,进一步比较现有土壤容重函数的适用性潜力。所选函数模型的RMSE值在0.121~24.602 mg/m3,波动幅度较大,其中Adams W A(1973)、Yang Y Q (2005)、HAN G Z(2016)-A与HAN G Z(2016)-C的RMSE值最小,在0.012~0.034 mg/m3。综合RMSE与ME值来看,HAN G Z(2016)-A模型模拟结果相对最好,该模型的RMSE值接近于0,ME值为-1.197 mg/m3,研究区土壤有机质含量较高,可能是其模拟结果较好的原因。Huntington(1989)与Benites V M(2007)模型模拟结果最差,其原因可能在于,研究区土壤生成环境的不同,Huntington的研究区位于新罕布什尔州一个23 hm2流域上的森林土壤区域,皖北平原区域特殊的地形地貌(淮河平原区)和气候背景(暖温带半湿润季风气候)与其差异较大。Benite等[4]曾就不同土壤母质生成环境对于现已发表的土壤容重函数的使用发出提醒。
在土层0~40 cm,与现存该地区最优模型HAN G Z(2016)-A相比,使用融合十折交叉检验的最优子集、lasso压缩估计所开发的函数模型精度从RMSE上来看提高了一个小数位(RMSE=0.121至0.063 mg/m3),这说明了本文所构建的模型相比于现存模型,其更好的适用于皖北平原地区。
3 讨 论
最优子集法和lasso法分别在不同垂直尺度下对土壤容重的集中与分散趋势进行了较好的预测。但从散点分布趋势中可以看出,模型中依然存在一些并未解释的变异性。除了一些数据本身无法解释的变异外,在模型中引入对时空要素的刻画可能会对模型的解释能力有显著的改善。Lark和Cullis等[21-23]利用采样点的坐标信息与克里金法对模型施加了空间相关结构,使模型的解释能力得到提升。段良霞[24]则以时间序列数据相互依赖为基础,通过空间状态模型和经典线性回归模型对该区不同尺度下的土层深度水含量进行预测,并得到了较好的预测效果。土壤各属性间的相关性大小,通常表现为单一剖面下采样数据高于在不同剖面下所获得的数据[25],这种存在于单一剖面下的特有的相关性也许可以反映出该剖面对于其内部各土壤属性所产生的各种微小、未知的影响。同时,这种特有的相关性也可能广泛存在于单一的采样区、研究区,甚至包括特定的植被类型、气候与年份下[16]。这种特有的相关性是很难被实际捕获或量化。若只特定研究某一剖面下土壤容重的转换函数,这种难以量化的特有的相关性则可以作为噪音进行处理,也即在一般回归模型下包含固定效应(各土壤属性对于容重的影响)和噪音(特定剖面对土壤各属性的影响)。但现有国内外研究[18,26-27]中,往往是基于大量不同土壤剖面下所采集的数据,此时的数据集中存在两种随机因素会影响模型的预测能力,一种是某个特定土壤剖面所具有的随机噪声,另一种则是因为剖面与剖面在空间或时间上的不同而形成的随机效应,这种存在于数据集中嵌套的随机因素结构通常会导致对数据中实际可用信息量的误判,也可能会对参数估计和假设检验的结果产生影响。

表3 国内外土壤容重转换函数
在土层0~40 cm下的土壤容重预测模型中,土壤采样深度在最优子集法与lasso法中均未被选入。这是因为表层土壤有机碳含量与土壤采样深度间的高度的相关性(corr.=-0.67**)所造成的模型过拟合而被剔除。同时,在很多土壤容重的预测模型的研究中,采样深度均不被认作是用于预测容重的可能性变量。采样深度可以用作容重的预测因子,但它只能描述了其变异性中较少的部分[7-8]。但上述这些研究多集中在土壤表层(0~30 cm),Qiao等[28]在中国黄土高原地区进行了土层50~200 m下的土壤容重模型的构建,模型中采样深度作为的容重变异性的重要解释因子,但这可能也与土壤有机碳在土层深处含量较低有关,进而提高了采样深度的重要性。在之前的研究中,一些学者将采样深度作为连续型变量代入模型中,并得出容重与采样深度呈现出显著的非线性关系[19,29-30]。由于大多数的土壤样本是在固定深度下进行采集,因此无需将此结论扩展到任意模型中。尽管已有研究说明,表层采样深度对于容重的预测并不起决定性作用,但本文还是建议将采样深度作为分类变量引入任何的模型策略中,因为随着土层深度的增加,土壤中各属性均发生变化。
4 结 论
对于当前研究现状的不足,本文选取了最优子集、lasso压缩估计与十折交叉检验法构建土壤容重转换函数,并探究其在研究区不同垂直尺度下对土壤容重预测的效果,获得以下结论。
(1)土壤容重数据服从正态分布(Skew.=-0.04,Kur.=-0.48);土层0~40 cm,土壤容重变异系数为5.07%,处于低变异水平。Pearson相关性表明,在不同垂直尺度下,土壤容重与土壤有机质、含水量、黏粒、粉粒、砂粒呈现出较低的线性相关性(corr.<0.5)。
(2)在土壤有机质含量较高土层中,土壤容重的系统变异性主要受土壤有机质影响,当有机质含量较低时,土壤质地、土壤含水量对土壤容重的影响程度得到提升;土壤采样深度因与有机质间高度的相关性(corr.=-0.67**)所造成的模型过拟合,固在最优子集和lasso压缩估计法均被剔除。
(3)基于融合十折交叉检验的最优子集与lasso压缩估计所得土壤容重预测值与实际值没有显著差异(P>0.05),但在土层0~10、10~20 cm,最优子集法较lasso法预测效果更佳(RMSE=0.070、0.054),土层20~40、0~40 cm,lasso法预测值则更为接近实际的土壤容重分布趋势(RMSE=0.070、0.029)。
上述两种方法构建的模型相比于现有土壤转换函数模型,更好的适用于皖北平原地区,可为类似区域的土壤容重研究提供方法支撑。
