基于学习率自增强的图像识别深度学习算法

吕 伏 刘 铁

1(辽宁工程技术大学基础教学部 辽宁 葫芦岛 125105)2(辽宁工程技术大学软件学院 辽宁 葫芦岛 125105)

0 引 言

深度学习(Deep Learning)[1]作为统计机器学习(Statistical Machine Learning)的重要分支，是目前人工智能领域备受关注的研究热点。卷积神经网络作为深度学习的重要推动力，近年来取得了重大的突破，在计算机视觉、自然语言处理和遥感图像理解等领域有出色的表现，被广泛地应用。

Hinton等[2]提出深度置信网络(DBN)，它是含多隐藏层、多感知器的一种网络结构，DBN强大的特征提取能力和“逐层初始化”特有的训练模式，有效地降低了Deep Learning模型的训练难度。与浅层学习模型相比，Deep Learning模型有更深的网络层次，通过构建复杂的非线性网络模型，对输入数据的特征进行分层学习，实现图像特征的有效提取，最后把低层学习到的特征组合为高层抽象的图像特征，完成对输入数据的分类识别。

深度置信网络的提出是深度学习发展史上的一个里程碑，从此，深度学习快速发展，并被应用到众多领域中。在图像识别过程中，为了解决特征提取困难、无法满足实时性要求等问题，Liu等[3]通过构建自适应增强模型，针对分类误差进行有目的的训练，实现了卷积神经网络模型的优化调整和分类特征的自适应增强，并且网络的收敛性能和识别精度有较大的提高。Liu等[4]提出一种结合无监督和有监督学习的网络权值预训练方法，实验验证该算法在解决训练过程中易收敛于局部最优值的问题上优于现有算法。Gao等[5]在卷积神经网络模型AlexNet[6]的基础上，提出了对数据集采用数据增强等预处理方法。实验结果表明，识别准确率和识别速度有一定的提升。Song等[7]提出基于深度神经网络模型的手写体图像识别方法，让机器自动学习特征，并在此基础之上改进成本函数，加入Dropout[8]防止过拟合，实验结果表明，该方法对手写体数字的识别有更加快速准确的识别效果，在识别准确率和实时性方面均有提高。He等[9]在汉字识别过程中结合卷积神经网络，取得了较好的识别效果并降低了训练时间。Chen等[10]提出的手写体数字识别模型，有较好的识别精度，模型的识别能力甚至超过了人类的识别能力。但是目前深度学习模型仍然具有收敛速度慢、识别精度不高、泛化性不足等问题。

学习率是一个非常重要的模型训练超参数，决定了迭代的步长。学习率过大会使代价函数直接越过全局最优点，使最优解在极值点附近来回震荡；学习率过小会使代价函数的变化速度很慢，增加网络模型收敛的复杂度，并很容易使最优解收敛于局部最小值。现有的神经网络模型，学习率一般是随着迭代次数进行衰减，这对神经网络模型的收敛速度和识别精度有很大的影响。因此在网络模型的训练过程中动态调整学习率就显得非常重要。

受文献[11]的启发，为了进一步提高深度卷积神经网络的收敛速度、识别精度以及网络模型的泛化能力，本文通过研究深度卷积神经网络训练过程中学习率的变化情况，提出一种学习率自增强算法，在网络训练初期，用大于1的常数自增强学习率，加快网络模型向极值点的逼近速度。随着训练的进行，根据网络模型代价函数的相对变化率，调整网络模型的学习率。实验表明，该方法可以有效地提高网络模型的收敛速度，并使最优解在极值点附近的震荡程度得到极大缓解。

1 相关工作

深度卷积神经网络是一种特殊的多层神经网络模型，在图像处理领域有着广泛的应用，深度卷积神经网络是受动物视觉神经系统的启发，用卷积层模拟对特定图案的响应，池化层用来模拟动物视觉皮层的感受野，一般由输入层、隐藏层和输出层组成，如图1所示。输入层是未经任何处理的二维原始图像，隐藏层通常为卷积层和池化层的重复结构，输出层是对特征进行分类和识别的结果，其中特征提取和分类是在隐层中进行的。深度卷积神经网络对图像的分类识别主要包括两个过程，即前向过程和反向过程。前向过程包括特征提取和分类，计算各个神经元的激励值和损失值，而反向传播主要是权值更新的过程。前向传播过程会产生分类误差，反向过程通过把前向传播产生的误差反馈到网络模型中从而实现对权值和偏置的更新。

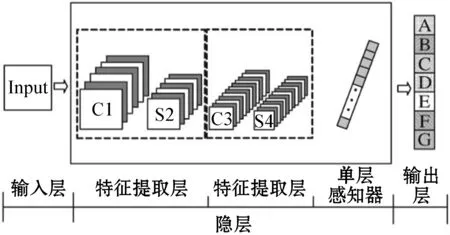
图1 卷积神经网络结构

设卷积层的第i个输入数据为Ii，卷积核为Wi，各有n个，偏置为Bi，激活函数为f，则卷积层输出特征的计算表达式为：

(1)

式中：con为卷积函数；Fc为卷积层输出的特征。

下采样操作是对卷积输出的特征做进一步的降维处理，并把对应输出输入到全连接层，全连接层经过权值变换和激活后得到本轮的分类结果，通过与分类真值比较，得到对应的分类误差。设全连接层的输入特征为T，对应的权值为W，偏置为B，激活函数为f，则全连接层进行分类的表达式为：

F0=f(W*T+B)

(2)

式中：F0为分类结果矩阵。

2 学习率自增强算法

2.1 代价函数

在机器学习中，经常选择代价函数作为优化的目标函数。代价函数指的是深度卷积神经网络模型的预测值和真实值之间的误差。样本数据集的代价函数定义为：

(3)

图2 ReLU函数图像

(4)

(5)

深度神经网络通过反向传播，将分类误差反馈到隐层中，使每层中的权值和偏置得到更新，进行下一次循环迭代时，使用最近更新后的各项参数进行网络模型的训练，通过不断的更新迭代，使网络模型中的识别率不断提高，损失函数降至最小。设l为学习率，则网络模型中的权值w和偏置b由w1和b1更新为w2和b2的表达式为：

(6)

(7)

由图2可知，ReLU激活函数是分段线性函数，自变量为负值或0时，函数值为0，自变量为正值时，函数值保持不变，这种操作被称为单侧抑制。在深度卷积神经网络模型中，由于梯度下降算法链式求导法则的乘法特性，存在梯度消失现象，通过使用ReLU激活函数，可有效地解决因为连乘而导致的梯度消失问题，整个过程的计算量较小，并且ReLU激活函数会使一部分神经元的输出为0，从而获得网络的稀疏性，减少了参数间相互依存关系，有效缓解过拟合问题的发生。但是ReLU激活函数的输出不是以0为中心，会使一部分神经元的输出为0，故随着训练的进行，有可能出现神经元“死亡”、权重无法更新的情况。因此，考虑到以上因素，本文提出学习率自增强算法，用大于1的常数自增强学习率，加快网络向极值点附近的逼近速度，随着训练的进行，根据模型代价函数的变化情况调整学习率，使得学习率的变化对于未知的数据更加敏感，提高了模型分类识别的性能。

2.2 基于代价函数变化率的学习率自增强算法

学习率是深度卷积神经网络模型训练过程中一个非常重要的超参数，它是梯度下降算法搜索过程的步长，对网络模型的性能有着非常重要的作用。学习率过大，将导致最优解在极值点附近来回震荡；学习率过小，将导致模型很难收敛或使得最优解收敛于局部最小值。因此，学习率对网络模型的收敛效果有极大的影响。而在以往的实验中，网络模型的学习率大多是根据经验来设定，在模型训练的整个周期中保持恒定或根据迭代次数进行衰减。在实际实验过程中，随着时间的推移，网络模型的学习情况复杂，在各个时期有很大的差异，因此，将模型的学习率设置为单一的不变量对模型的学习性能有重要的影响。本文提出的学习率自增强算法是受自适应调整学习率算法[11-12]启发，根据模型训练过程中各个阶段代价函数的变化情况调整学习率，相比于恒定的学习率，使用学习率自增强算法可以提升模型的性能，缩短训练的时间。在模型训练初期，为了加快网络的收敛速度，用大于1的因子自增强学习率，加快网络向极值点附近逼近的速度。随着训练的进行，由于模型接近收敛，因此在该阶段根据代价函数的相对变化率适当的增加或减小学习率，直至网络收敛或是达到设定的迭代次数。

第n个世代的学习率ln可以表示为：

(8)

(9)

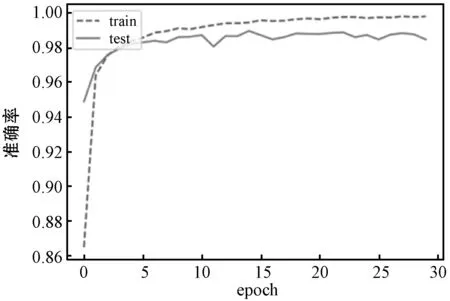
式中：l0为初始学习率；α(x)为代价函数的相对变化率；J(x)、J(x-1)分别为x轮和x-1轮的代价函数；本文设置阈值0

本文提出的学习率自增强算法，根据当前网络模型的训练世代数(epoch)和代价函数的相对变化率进行适当的更新，步骤如下：

Step1判断当前训练的世代数，若小于等于b，执行Step 2；若大于b，则执行Step 3。

Step2用大于1的常数自增强学习率。

Step3按式(3)计算代价函数的值，求出代价函数的相对变化率。

Step4若代价函数变化率小于0，则按ln=ln-1(1-aα(x))调整学习率;否则，按ln=ln-1(1-α(x))调整学习率。

Step5按式(6)和式(7)更新权值和偏置。

Step6当未达到设定的迭代次数时，返回Step 1继续执行;否则停止迭代，训练完成。

在网络训练的前b个世代，通过大于1的常数λ自增强学习率，从b+1世代以后，判断当前代价函数的相对变化率，如果代价函数的变化率大于0时，则根据代价函数的变化率适当的减小学习率，当代价函数变化率小于0时，则根据初始学习率和迭代次数适当的增大学习率。经过多次参数训练，得到公式中较优的参数取值为λ=1.05、b=4，即在模型训练的前4个世代用1.05的倍数自增强学习率。

3 实验与结果分析

本文实验是在Python环境下，采用Pytorch框架，基于AlexNet深度卷积神经网络实现图像分类识别[13]，网络设计5个卷积层，5个池化层，采用固定卷积核，使用最大值池化方法，所使用计算机的CPU型号为Intel(R)Core(TM)i7- 4700MQ，内存为16 GB。实验共分为两个部分，第一部分是在MNIST数据集[14]上对手写数字进行识别，验证本文算法对图像识别能力的优化效果；第二部分是在CIFAR-10数据集[15]上对图像进行分类识别，验证本文算法对一般图像的普适性。MNIST、CIFAR-10数据集中的部分样本如图3所示。

(a) MNIST手写数据集

(b) CIFAR-10数据集图3 数据集部分样本

根据式(8)和式(9)得到本文网络模型训练过程中代价函数和学习率的变化情况如图4所示。

(a) 代价函数

(b) 学习率图4 实验结果

3.1 手写数字数据集实验与分析

实验使用MNIST手写数字数据集，对学习率自增强的AlexNet[16]神经网络模型的性能进行测试和验证，MNIST数据集中共有7万条数据，其中6万条作为模型的训练数据，1万条作为验证模型识别准确率的测试数据，每个样本为28×28的灰度图像，0到9共10类的手写数字，在输入神经网络模型前，将样本进行归一化处理。使用本文中的学习率自增强算法作为网络模型的优化算法，每批次样本大小为256，共训练30代。在模型训练阶段，在全连接层引入Dropout，有效地避免过拟合问题，可消除全连接层对实验结果的影响。对结合本文算法的AlexNet网络模型在MNIST数据集上进行实验，记录图像分类结果的准确率情况，并绘制相应的曲线图。随着迭代的进行，准确率情况如图5所示。

图5 学习率自增强算法的识别准确率

可以看出，随着迭代的不断进行，学习率自增强算法的识别准确率不断上升，到达一定程度后，准确率不在变化，网络模型收敛，所以本文算法能够更好地反映学习率自增强的网络模型学习效果。

3.2 CIFAR-10数据集实验与分析

CIFAR-10数据集是由10类32×32的彩色图片组成，共6万幅图片，每一类包含6 000幅图片。CIFAR-10数据集被划分为5个训练的batch，每个batch包含1万幅图片，测试集batch的图片是由从每个类别中随机挑选1 000幅图片组成。在进行模型训练之前，同样需要将样本进行归一化处理。

相比于MNIST数据集，CIFAR-10数据集在每个类别中的差异相对较大，同时受姿态、颜色、背景等影响，在CIFAR-10数据集上的实验难度相对较大。在CIFAR-10数据集上，K-means+SVM[17]的识别准确率达到了79.60%。各种网络模型的识别准确率如表1所示。

表1 CIFAR-10数据集上各方法的识别准确率(%)

在CIFAR-10数据集上本文算法的实验结果如图6所示。

图6 CIFAR-10数据集误识率

由上述两个实验结果可以看出，结合本文算法的网络模型在一定程度上优于传统方法，但是在CIFAR-10数据集上的效果不如更深层次的网络，相比于Highway、ResNet等深层网络，本文算法的识别能力有限，存在一定的差距。

4 结 语

本文提出的学习率自增强图像识别算法，在网络模型训练阶段提高了调整学习率的灵活性，在迭代初期，能加大网络模型学习的步长，加快模型的收敛速度，当逼近最优解附近时，能根据代价函数的变化动态的调整学习率，避免出现震荡的情况。实验结果表明，该方法能在更小的迭代次数下接近最优解，有较好的收敛性，在一定程度上提高了图像识别的准确率。

由于本文实验的数据集为随机选取的图像数据，因此下一步研究工作将是如何设计更加有效的优化方法和正则化约束，进一步提高算法的识别准确率。另外，随着网络层数的增多，模型的学习能力越强，但耗时也相对增多，因此，如何兼顾效率和时间也是未来的一个研究方向。