基于新型倍压单元的准Z源耦合电感高电压增益DC-DC变换器
2021-12-14周雪松马幼捷
卫 科 周雪松 马幼捷 李 微
1(国网晋城供电公司 山西 晋城 048000)2(天津理工大学电气电子工程学院 天津 300384)
0 引 言
伴随着全球性能源危机和全球变暖问题的日益严峻,新能源的开发与利用在世界范围内快速推进,光伏、风能等清洁能源均得到了发展,在光伏发电并网系统中,光伏电池组在并网过程中需要用到大功率高增益的DC-DC直流变换器以解决光伏储能装置的电压远低于电网所需要的高电压之间的矛盾。近年来,升压变换电路的发展主要分为两部分:隔离型与非隔离型,其中非隔离型的高增益直流变换器主要拓扑结构有开关电感、开关电容、耦合电感和由二极管和电容器组成的倍压单元。
Boost直流变换器是经典的升压变换器,但是其升压增益特性有限,不适用于高功率场合。文献[1-3]将传统Boost的输入电感用耦合电感代替,并将耦合电感的副边与输出二极管串联,降低了变换器增益对占空比的依赖,避免变换器工作在极限占空比状态,提高了变换器增益范围,但是依然存在输入电流不连续、动态元件过多等问题,不适用于光伏系统。为了解决上述问题,文献[4]中提出了一种改进型的基于开关电容的Z源逆变器,与传统的Z源逆变器相比,它可以实现输入电流的连续,但升压能力没有提升。文献[5]提出了准Z源结构,具有输入电流连续、电容应力低、输入与输出共地等优点从而得到了广泛的应用。
目前倍压单元用于提高直流变换器增益的研究较为广泛[6-7],文献[8]提出了一种新型的耦合电感倍压单元,并将该单元应用在了传统的Boost中,但其存在升压能力有限、输入电流不连续等问题。本文提出了一种基于新型倍压单元的准Z源耦合电感直流变换器,显著提升了电压增益,减小器件应力,同时提高了变换器效率。
本文变换器拓扑如图1所示,电路由电感L1,电容C1、C2、C3、C4,耦合电感L2、L3,二极管D1、D2、D3、D4,开关管S组成。其中耦合电感由漏感Lk、励磁电感Lm和变比为Np∶Ns的一个理想变压器等效[9]。

图1 高增益直流变换器拓扑
1 电路特性分析
1.1 工作模态分析
1.1.1电感电流连续状态
变换器工作在电感电流连续状态时,其主要元件的工作波形和模态划分如图2所示。

图2 电感电流连续工作波形图
模态1(t0-t1):t1时刻之前,开关管S导通,在这一时间段内,输入电压源Vin与C1通过开关管S给电感L1储能,C2通过开关管S向漏感Lk和励磁电感Lm储能,耦合电感原边电压左正右负,电流由同名端流入,并向耦合电感的副边感应上正下负的电压,产生由同名端流出的电流向倍压电容C3、C4充电。此时间段内iL1、iLk、iLm和iL3线性上升,C1、C2电压下降,C3、C4电压上升,二极管D1、D2截止,D3、D4导通,负载R由电容Cf供电。
(1)
(2)
式中:N=Np∶Ns。
(3)
模态2(t1-t2):t1时刻,控制开关管S使其关断,上一模态的能量传输通道关闭,二极管D1承受正向电压导通,由输入电压源Vin与C2通过D1向电感L1充电,iL1线性上升。漏感Lk向电容C1充电,漏感两端电压变为左负右正,励磁电感电压方向不变,因漏感值较小,故漏感电流减小很快,副边耦合电感电流iL3快速减小,iLm继续线性上升,电容C1、C2两端电压开始上升。
(4)
(5)
模态3(t2-t3):t3时刻之前,开关管S仍处于关断状态。T2时刻,耦合电感副边电流iL3减小为0,此时间段内副边电流iL3反向并线性增大,励磁电感上的电流iLm线性减小。此时二极管D2导通,D3、D4反向截止,电感L1耦合、电感的励磁电感Lm、耦合电感副边上的电流iL3和电容C3、C4共同向负载供电。
(6)
(7)
模态4(t3-t4):t4时刻,开关管S导通,二极管D2处于反向恢复状态,副边电感上电流iL3上电流快速下降为0,二极管D1截止。电容C1电压开始下降,漏感电流开始上升,从下一时刻开始,电路重新工作于模态1。
(8)
(9)
(10)
1.1.2电感电流断续状态
变换器工作在电感电流断续模式时,其主要工作波形和模态划分如图3所示。
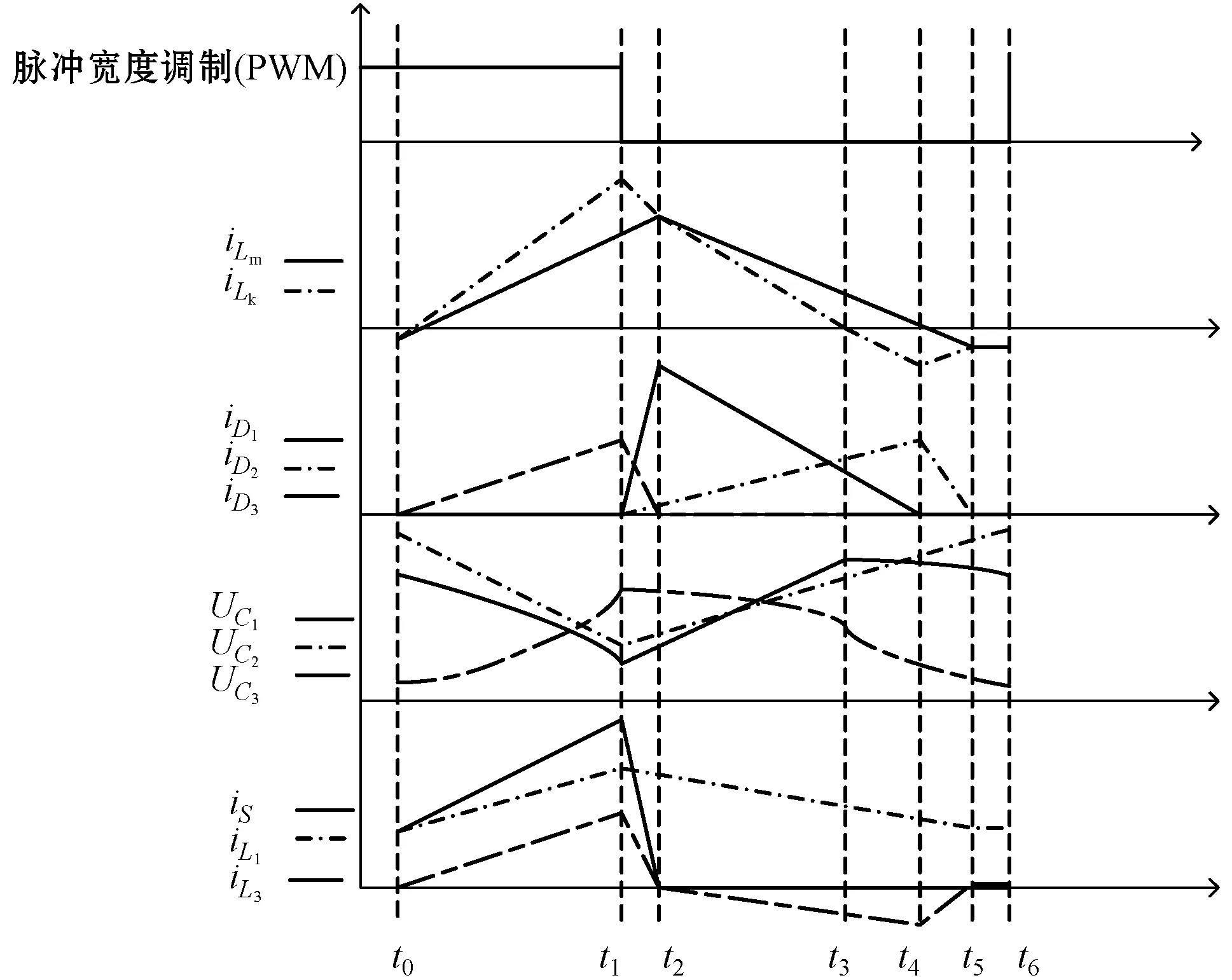
图3 电感电流断续工作波形图
模态1(t0-t1):在t1时刻之前,开关管S导通,电感L1、L2和Lk分别由输入电源、C1和C2供电,耦合电感原边电压左负右正,电流从同名端流入,在耦合电感副边产生由同名端流出的感应电流为倍压电容C3、C4供电。此时间段内对应的电流表达式为式(1)-式(3)。
模态2(t1-t2):在t1时刻,开关管S被控制关断,二极管D1承受正向电压导通,电容C1、C2分别由漏感Lk和输入电源供电,漏感两端电压变为左负右正,但是励磁电感电压的方向不变,且电流继续线性上升。对应电流表达式同式(4)-式(5)。
模态3(t2-t3):开关管S仍然处于关断状态,t2时刻耦合电感副边电流减小为0,然后反向并线性增大,二极管D2承受正向电压导通,D3、D4截止,漏感与励磁电感上的电流线性减小,电容C1、C2电压上升,倍压电容电压下降,输入电源Vin、输入电感L1和励磁电感Lm向负载供电。相对应的电感电压表达式同式(6)-式(7)。
模态4(t3-t4):t3时刻,漏感上的电流减小为0,输入电源、L1、励磁电感与C1向电容C2与耦合电感副边供电,C1上的电压开始下降,漏感上开始电流反向增加,副边电流线性上升并继续向负载供电。
模态5(t4-t5):开关管S状态不变,t4时刻,漏感电流开始反向减小,二极管D1反向截止,耦合电感副边感应电流iL3也开始反向减小。励磁电感上的电流减小为0并反向继续增加。
模态6(t5-t6):开关管S状态不变,t5时刻,副边电流减小到0,二极管D2反向截止。输入电源与输入电感L1向漏感Lk和励磁电感充电,漏感与励磁电感上的电流线性上升。电路工作状态与连续模式的模态4相同。直到下一个周期到来开关管S导通,电路重新工作于模态1。
1.2 高升压增益特性分析
根据上述的工作模态分析,可以看出工作于电感电流连续模式的新型倍压单元和耦合电感的高增益直流变换器的四个模态中,模态2与模态4所占时间都很短,所以主要考虑模态1与模态3。由电感伏秒平衡原理,分别得到L1、L2与Lk的伏秒平衡方程式为:
(11)
式中:D为占空比;K为耦合电感的绕组系数。
由模态3可得:
V0=VC2+VC3+VC4+VC1+NVC1
(12)
由式(11)、式(12)可得:
(13)
式中:Vg为输入电压。
将式(13)代入式(12)得到增益M为:
(14)
1.3 器件应力分析
根据上述由增益分析可得开关管S在关断期间的电压应力:
(15)
则:
(16)
二极管D1、D2、D3、D4电压应力:
(17)
(18)
(19)
综上,相比于传统准Z源变换器的开关管与二极管电压应力V0/(1-D)[10],本文提出的新型变换器的二极管应力得到了显著的降低。
由模态分析可知,一个周期内,流经电容C3、C4的电流平均值为0,因此一个周期内耦合电感的副边电流iL3的平均值为0,则原边电流iL2平均值也为0,由伏秒平衡原理可得电容C1、C2上电流平均值为0,则可以得到电感L1上的电流iL1与励磁电感电流iLm在一个周期内电流平均值为输入电流Iin。开关管S在导通状态下流经二极管D3、D4,在关断状态下流经二极管D2,由电容安秒平衡原理,可知流过二极管D2的电流平均值ID2即为输出电流I0,同理,二极管D3、D4上的电流平均值ID3、ID4亦为I0/2,参考iL3的波形图可得:
(20)
式中:iL3_on与iL3_off分别为副边电流在开关管导通和关断状态下的峰值。iL3_on和iL3_off的计算如下:
(21)
(22)
则可以得到二极管D1、D2、D3和D4的电流应力为:
(23)
(24)
(25)
图4为当耦合系数k=1、匝比N=3时不同变换器的电压增益M与占空比的关系图,可以看出,相同占空比的情况下,本文所提变换器的电压增益显著高于传统的Z源变换器。

图4 变换器增益曲线对比
1.4 电路参数设计
由增益表达式可以看出,变换器占空比应被限制在0~0.5之间,同时避免占空比在此区间内过大或过小。占空比过小,增益可能达不到所期望的值,占空比过大,由应力分析可知会导致元器件电流应力过大,电路中出现电流尖峰等对元器件产生损害并会增大损耗[11-12]。故权衡考虑电流和电压应力,选择占空比D=0.3,耦合电感匝比N=3。设计额定输入电压25 V,额定输出电压220 V,额定功率500 W。
1.4.1电感参数设计
准Z源直流变换器工作在电感电流连续状态与不连续状态的临界条件为:

(26)
根据模态3,在开关管S导通期间,由基尔霍夫电压定律可得:
(27)
要使变换器工作在电感电流连续模式,L1应满足:
(28)
同理可得励磁电感Lm应满足:
(29)
1.4.2电容参数设计
由式(13)的电容电压分别为:
(30)
电容器的电压纹波为:
(31)
选择电容C1、C2、C3、C4的电压纹波ΔC1、ΔC2、ΔC3、ΔC4为电容电压的1%。可得电容值为:
(32)
(33)
(34)
在选取电容器的参数时,选择的电容值越大,则等效的串联电阻就越小,因此考虑到损耗的因素,往往选值比上述值更大一些[13]。
1.4.3开关器件选择
根据前面对器件应力分析式(16)可得:
(35)
开关管闭合时,开关管S的电流平均值:
(36)
则有效值为:
(37)
根据上述电压电流应力计算,选择开关管型号为IPP110N20N3G。
根据式(17)-式(19)可得二极管的电压应力分别为:
(38)
根据式(23)-式(25)可得二极管电流平均值:
(39)
根据上述二极管电压与电流的应力参数,D1选择型号为STTH3003CW,D2选择型号为STTH3003CW,D3、D4选型号为STTH6002C[14]。
2 功率损耗分析
2.1 MOSFET功率损耗
MOSFET的损耗主要包括两部分:通态损耗、开关损耗。通态损耗电流有效值和导通电阻计算得到:
(40)
开关损耗分两部分计算,首先是开通损耗:
(41)
式中:UDS为开关管S上的电压;tr为开关管S的导通时间。
第二部分为关断损耗:
(42)
式中:tf为开关管S关断时间。
则MOSFET总损耗:
PMOS=P0+Pon+Poff=7.13 W
(43)
2.2 二极管损耗
二极管的功率损耗为二极管的正向压降与二极管导通时的平均电流相乘得到:
PD=PD1+PD2+2PD3=1×20×0.7+1×3.75×
0.7+2×0.75×4.38×0.3=18.596 W
(44)
2.3 电容功率损耗
电容功率损耗主要由电容串联等效电阻造成[15]。查询得到470 μF与47 μF的等效串联电阻分别为120 mΩ与50 mΩ,由RESR表示。计算可得电容功率损耗为:
(45)
(46)
(47)
电容损耗合计为:
PC=PC1+PC2+PC3=8.37 W
(48)
2.4 其他功率损耗
其他损耗主要指耦合电感的磁芯产生的损耗,常用磁芯损耗约为1.6 W,则系统磁芯损耗为3.2 W,则可得变换器效率为:
(49)
3 仿真分析
3.1 数学建模与频域分析
为了更好地分析变换器的稳态性能和动态性能,本节将对变换器进行系统建模和频域分析,由于变换器中含有二极管和全控型开关管等非线性元件,因此属于非线性时变系统。但是当直流变换器工作在稳态时,其小信号变换量之间可以等效看作为线性关系。目前普遍采用状态变量平均法对变换器进行建模,状态空间平均法是指对非线性的系统,利用平均法的一阶近似建立线性的数学模型,从而使非线性的系统可以得到线性模型,可以使用经典的线性控制理论对其进行稳态和小信号分析。
状态空间平均法的基本思想是根据占空比将开关管不同状态下的状态方程进行平均化处理,以电感电流和电容电压作为状态变量,输出电压和电流作为输出变量,建立系统平均状态方程。

(50)
式中:x为系统状态变量;y为输出变量;a、b、c为未知系数。设变换器工作在稳态时(满足低频假设与小波纹假设),则根据占空比对前面所分析的模态1开关管导通时的状态方程系数A1、B1、C1与模态3开关管关断时的状态方程系数A2、B2、C2根据式(51)得到平均状态方程。
(51)
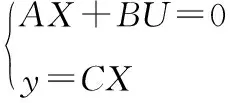
(52)
其中:


将本文变换器参数代入,由于本文变换器中储能元件较多,为高阶状态方程,故直接求解了系统的数值表达传递函数如式(53)所示。
Gvs=
(53)
根据式(53)绘制系统的开环伯德图如图5所示。

图5 系统开环伯德图
从图中看到系统幅值裕度-1.94 dB,相位裕度-49.3°,不能满足工程使用要求,根据系统开环频域特性,为了增加变换器闭环传递函数的稳定性,增加系统相位裕度,综合考虑后选择超前校正作为其补偿网络的设计方案。
本文设计校正网络增加增益环节,传递函数表达式为:
(54)
式中:α为分度系数;TS为时间常数;k为增益值。由式(54)可知,采用此补偿网络时,系统整体的增益会下降a倍,因此需要提高放大器增益用以补偿。由开环频率特性可知,系统开环相位裕度r0=-49.3°,而一般系统要求相位裕度r应该在45°左右。考虑误差ε,根据所期望的相位裕度可得系统最大超前角度:
φm=r-r0+ε=105°
(55)
其中最大超前角度:
(56)
可以计算出:
(57)

(58)
将上述的参数代入超前补偿的传递函数中,可得不加增益补偿时的传递函数如式(59)所示,伯德图如图6所示。
(59)

图6 不加增益时校正后的系统伯德图
可以看出,此时系统在期望截止频率的增益裕量约为10 dB,由:
L(ωc)=-20lgk
(60)
可得k=0.316,则可以得到完整的校正环节传递函数如下:
(61)
根据伯德图如图7所示,可以看出,系统加入校正环节后,其相位裕度明显改善达到了47.7°,符合期望值的45°左右,幅值裕度为13.6 dB,也是比较理想的,期望值10 dB左右,截止频率为ωp=1.46×104rad/s,在开关频率的五分之一左右。同时系统的稳态误差也得到了一定程度的减小,满足了工程应用的性能指标。

图7 加增益校正环节后系统伯德图
3.2 PSIM仿真
根据设定条件,经过优化的电路仿真参数如表1所示。

表1 仿真参数
根据上述参数,在仿真软件PSIM中搭建了一个500 W的仿真模型。
图8为输入电压Uin、输出电压U0的波形。增益效果与理论分析基本一致,当占空比为0.3时,输出电压约为370 V,略低于理想增益的输出380 V,这是因为在仿真过程中加入了漏感,导致耦合电感系数降低,储能电容的充电速率受到影响,倍压电容没有达到理想增压效果。

图8 25 V输入380 V/500 W电感电流连续模式输出仿真图
由图9可见,25 V输入、380 V/500 W输出情况下的开关管S、二极管D1和二极管D2电流应力分别为62 V、250 V左右,与理论分析基本一致,可以看出其中开关管的电压应力为V0/(1+N(2-D)),低于传统准Z源耦合电感的开关管应力V0/(1+D(N-1)),输出二极管的电压应力为V0(1+N)/(1+N(2-D)),低于传统准Z源耦合电感输出二极管的应力V0。相比传统的拓扑,本拓扑在进一步提高增益的同时降低了开关元件的电压应力。

图9 25 V输入380 V/500 W电感电流连续模式开关元件应力仿真图
从图10可以看到,电容C1、倍压电容C3、励磁电感与漏感的工作波形,与理论分析一致,验证了理论分析的正确性。

图10 25 V输入380 V/500 W电感电流连续模式工作波形仿真图
图11为电感电流断续模式下输入与输出波形,也实现了理想的高增益,图12为断续模式下各个元件的工作模态图,其中励磁电感电流出现负值,输出二极管D2提前截止,变换器工作状态与理论分析的模态图形一致,验证了理论分析的正确性,也实现了电压的高增益。
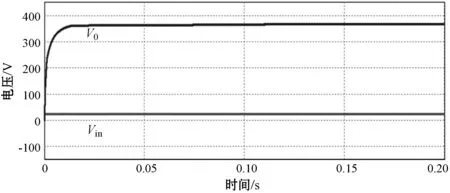
图11 25 V输入380 V/500 W电感电流断续模式输入输出仿真图

图12 25 V输入380 V/500 W电感电流断续模式工作模态仿真图
4 结 语
本文提出一种基于新型CLC倍压单元的准Z源耦合电感高增益的非隔离直流变换器拓扑,该拓扑解决了传统非隔离直流变换器电压增益有限、开关元件应力大、输入电流不连续等诸多问题。对系统进行了建模和频域分析,验证了系统闭环应用中的良好性能。按照500 W的PSIM仿真结果,可以看到:通过倍压单元的改进,该拓扑在适当的占空比与耦合电感匝比情况下显著提高了直流变换器的电压输出,达到了理想电压增益,同时进一步降低了开关元件的电压与电流应力,提高了变换器的可靠性,提高了变换器转换效率,在电感电流连续模式下满载效率可达93.05%。
