NOMA系统中基于全面学习粒子群算法的功率分配优化*
2021-12-14徐佳程嘉蔚柏仕超李晓辉王艺玲
徐佳,程嘉蔚,柏仕超,李晓辉,王艺玲
(安徽大学电子信息工程学院,安徽 合肥 230039)
0 引言
随着移动互联网的不断发展,移动数据呈现出快速增长的趋势,传统的正交多址(OMA,Orthogonal Multiple Access)技术已经满足不了海量的连接需求[1-2]。为了解决这些问题,5G 中引入了新型多址接入技术[3-4]。其中,非正交多址(NOMA,Non-orthogonal Multiple Access)技术是下一代蜂窝通信中最具有潜力的技术之一[5-6]。NOMA 技术集时域、频域和功率域于一体,并在发送端引入了功率域复用技术[7],使多用户能够共享资源,摆脱了传统的单用户独享资源的限制。
由于NOMA 系统具有功率域复用的特性,所以对功率合理分配是一个关键性问题[8-9]。参考文献[10]中介绍了全搜索功率分配算法(FSPA,Full Search Power Allocation),该算法是实现NOMA 系统最佳性能的功率分配方案之一。但是当用户数增加时,计算复杂度甚高,在实际操作中难以实现。参考文献[11]中介绍了固定功率分配算法(FPA,Fixed Power Allocation)和分数阶功率分配算法(FTPA,Fractional Transmit Power Allocation),其中,FPA 算法虽然减少了计算复杂度,但是没有考虑信道状态对功率分配的影响,所以得到的系统性能并不是最佳的;而FTPA 算法是在FPA 算法的基础上,引入了动态的功率分配因子,保证了低信道增益用户的吞吐量,符合实际操作环境[12]。参考文献[13]中介绍了迭代注水功率分配算法,有效降低了计算复杂度,但是在降低能耗方面还有所欠缺。
采用粒子群算法(PSO,Particle Swarm Optimization)进行功率分配可以实现节能减耗的目标,使能量效率最大化。参考文献[14]中介绍了采用原始粒子群算法进行功率分配的方法,但原始粒子群算法存在容易早熟收敛的缺陷,并且粒子在搜寻最优位置时会不断地向个体最优值和全局最优值靠近,即使当前搜寻到的最优值已经偏离了全局最优值,粒子还是会继续跟随当前的最优值,这将会导致粒子陷入局部最优,最终找到的最优值可能会偏离全局最优值[15]。为了解决这个问题,本文结合全面学习的粒子群算法(CLPSO,Comprehensive Learning Particle Swarm Optimization)[16]进行功率分配,全面学习粒子群算法可以有效提高种群的多样性,避免了早熟收敛和局部最优的缺陷,从而使系统能量效率得到优化。本文首先通过建立NOMA 下行链路能量效率系统模型,将功率分配优化问题等效成函数优化问题,其次采用了全面学习粒子群算法进行求解,最终获得更优的功率分配,使系统能量效率得到有效提升。
1 NOMA下行链路系统模型
对于单小区多用户NOMA 下行链路系统,系统模型如图1 所示。信道模型选择瑞利衰落信道,假设一个基站同时服务于K个用户,基站和用户之间以单天线进行数据交互,并且基站可以获得完全的信道状态信息(CSI,Channel State Information)。
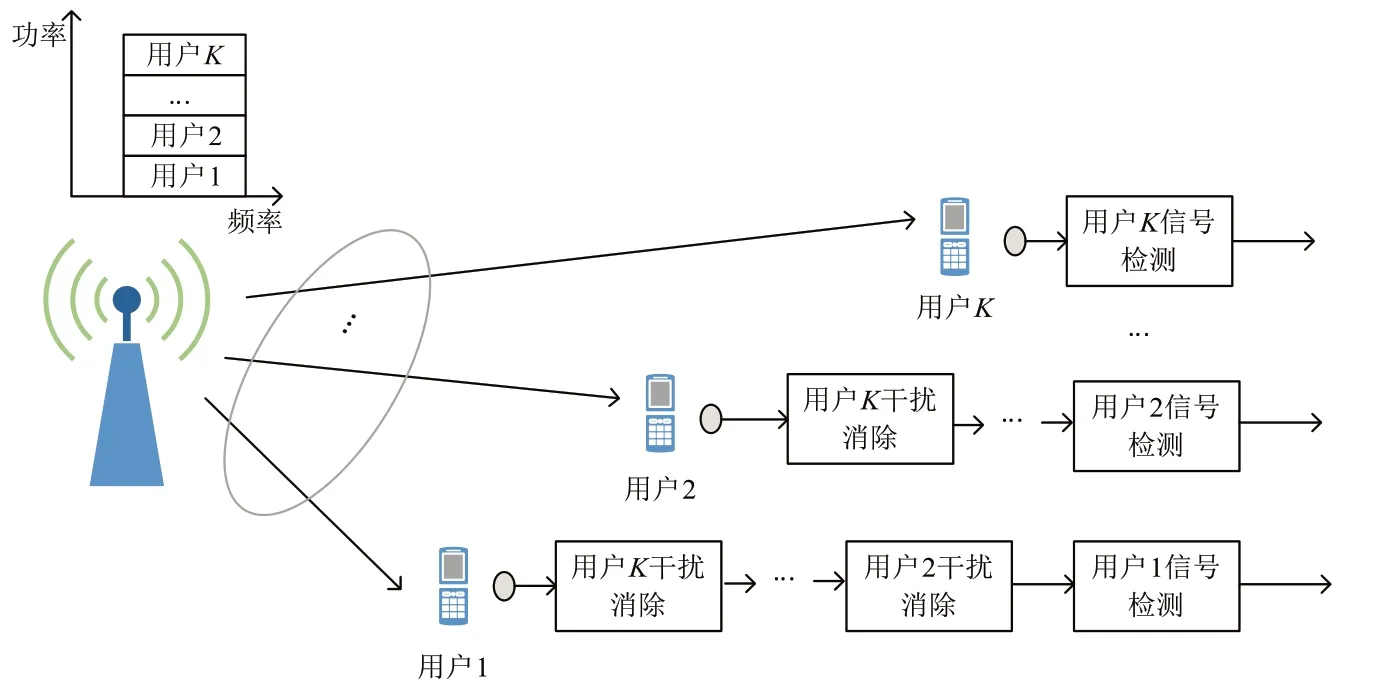
图1 NOMA下行链路系统模型
基站作为发射端在该子载波上发送的叠加信号为:

式中,hi为信道增益,ni为接收机ui处的加性高斯白噪声。这里将噪声设为方差为δ2且均值为零的高斯白噪声。
基站和用户ui之间选择瑞利衰落信道作为传输信道模型,可表示为:

式中,gi为瑞利衰落系数,Pi为用户ui在该子载波上的传输功率。L-1(di)为路径损耗,di为基站到用户ui的距离,用户ui在该子载波上的发送信号为si,假设si为标准化的,即E{si2}=1。
假设用户u1为小区中心用户,用户uK为小区边缘用户,则他们的信道增益从大到小排序为:

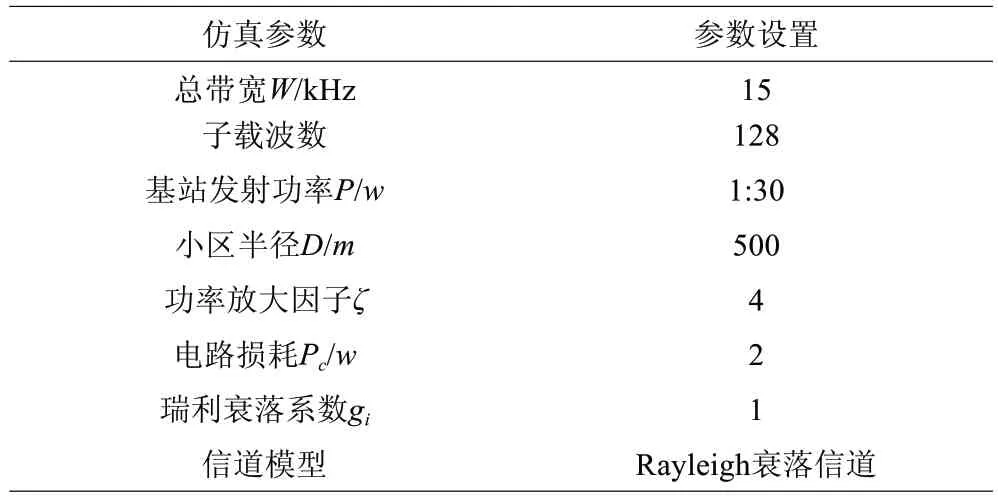
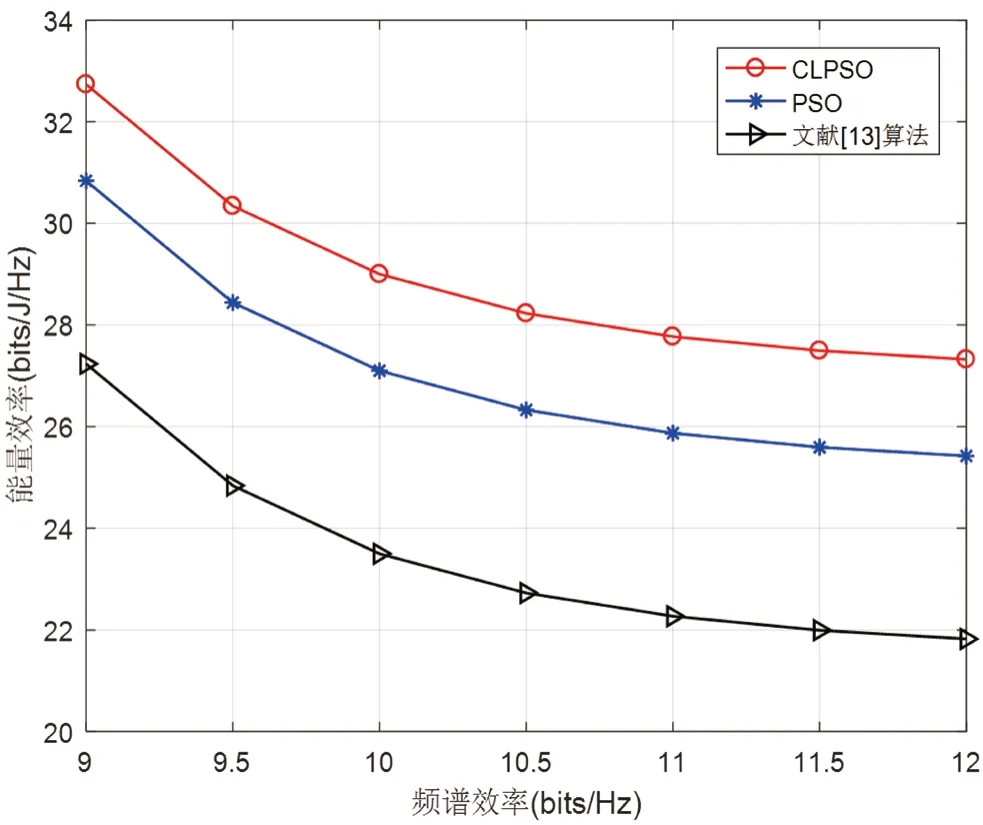
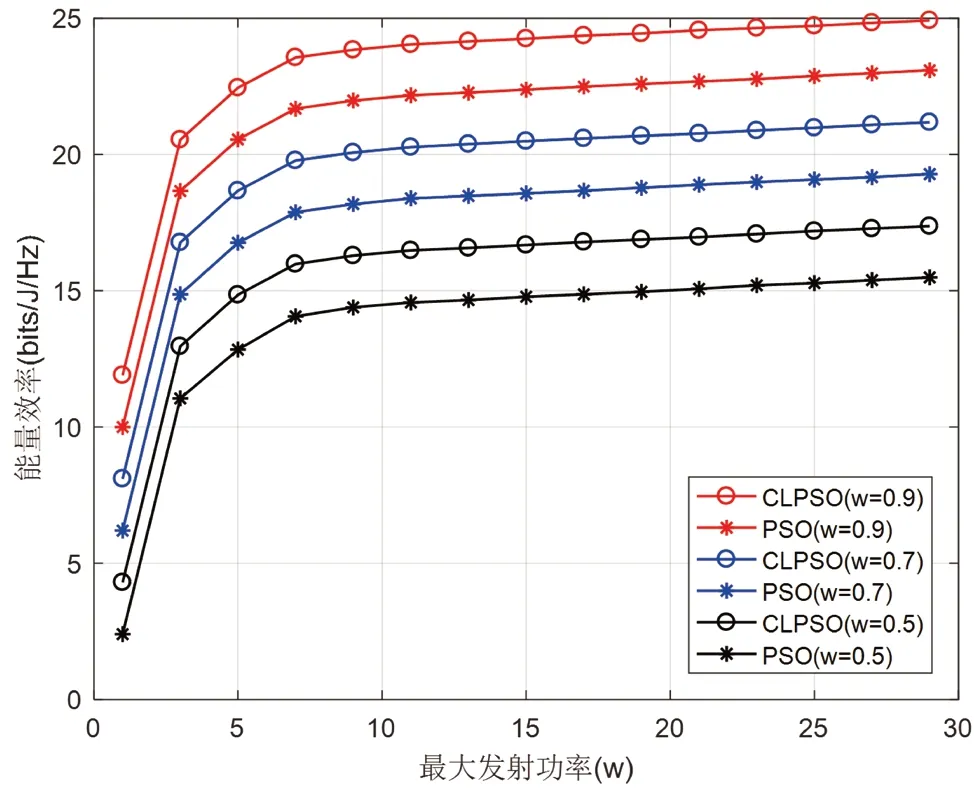
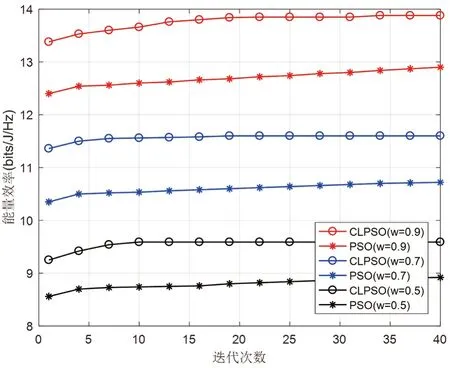
在此下行链路系统中使用串行干扰消除(SIC,Successive Interference Cancellation)技术进行信号的检测处理,假设用户ui(j 式中,W为基站的总带宽,其他用户的速率可表示为: 在无线通信系统中,频谱效率定义为系统传输的有效信息速率除以通信信道带宽,能量效率定义为有效信息传输速率与信号发射功率的比值。所以,NOMA 系统的能量效率和频谱效率分别为: 式中,ζ表示功率放大因子,Pc为电路损耗功率,基站的总功率为: 式中,Rimin为用户ui的最低速率要求,约束条件C1表示用户功率不小于0 且不大于基站总功率P;约束条件C2表示保证用户的最小速率;约束条件C3表示确保小区边缘用户的发射功率大于小区中心用户的发射功率。 为了提高NOMA 系统能量效率,本文采用全面学习粒子群算法进行功率分配。粒子群算法是将优化问题的解抽象成种群中的粒子,每个粒子通过学习自身飞行经验和其他粒子飞行经验来调整飞行的速度和位置,最终找到最优解。全面学习粒子群算法即为使用其他粒子的历史最好信息更新粒子速度的策略来改进粒子群算法。粒子可以更加全面地向群体最优位置Gbest、自身最优位置gbest及其他粒子的历史最优位置pbest学习,避免陷入局部最优。 式中ω为惯性权重,c1和c2为加速因子,r1和r2是属于(0,1)上的随机数。 惯性权重的取值直接影响算法的搜索能力,本文分别设置惯性权重ω为0.9,0.7 和0.5 来研究不同惯性权重情况下对能量效率的影响。 在NOMA 系统中采用全面学习的粒子群算法进行功率分配时,首先,将功率分配因子ei作为粒子在粒子群中的位置: 其次,设置功率分配系数范围为(0,1),即粒子的飞行范围。最后,将NOMA 系统的能量效率作为粒子群的适应度值,即f=ηEE,使用预定义的适应度函数来度量每个粒子的性能,最终求得的最优值即为最优功率分配方案。 全面学习的粒子群算法将自身飞行经验和其他粒子的飞行经验合并为一项,粒子的飞行速度更新方式为: 该算法中每个粒子在不同维度上通过相应的概率选择其他维度上的历史最优位置,摆脱了单纯学习自身最优位置的局限性,在一定范围内增加种群的多样性。pci为学习比例,阈值pci可表示为: 假设信道状态是已知的,并且无线信道为独立均匀分布的瑞利衰落信道。设置用户数K=20,功率域叠加用户数为2。在实际通信中,距离基站越近的用户信道增益越大。为了模拟实际通信,距离基站近的用户可视为小区中心用户;距离基站远的用户可视为小区边缘用户。迭代次数T=40,粒子的学习因子c1,c2=2。仿真参数如表1 所示: 表1 仿真参数设置 能量利用效率η可表示为: 图2 中不同频谱效率下采用全面学习粒子群算法、原始粒子群算法和文献[13]算法得到的能量效率的值如表2 所示。 图2 不同优化指标下系统能量效率和频谱效率的关系 采用全面学习粒子群算法、原始粒子群算法和文献[13]算法对NOMA 下行链路进行功率分配时能量效率和频谱效率的关系如图2 所示。由图可见,随着频谱效率的增加,能量效率不断降低。本文提出的全面学习粒子群算法所得到的能量效率优于原始的粒子群算法和文献[13]算法的能量效率,通过对表2 中的能量效率数值计算分析,采用全面学习粒子群算法得到的能量效率比采用原始粒子群算法和文献[13]算法得到的能量效率分别提升了6.6% 和19%,这表明采用全面学习粒子群算法得到了更优的功率分配因子。 表2 不同优化指标下得到的能量效率数值 在图3 中,比较分别通过全面学习粒子群算法和原始粒子群算法进行功率分配时,基站最大发射功率对系统能量效率的影响。随着基站最大发射功率的逐渐增加,在最大发射功率为0~5 W 的范围内时,能量效率迅速增加,而在基站最大发射功率大于5 W 之后,能量效率增加减缓,最后趋于不变。这是由于在初始阶段,基站的最大发射功率对系统能量效率约束相对较大,随着基站对系统能量效率的不断优化,最终趋近最优解,得到最优功率分配因子,此时继续增加发射功率,基站不会再消耗冗余的功率,系统的能量效率逐渐达到平衡。从图中可以看出,全面学习粒子群算法比原始粒子群算法得到更优的系统性能,并且在惯性权重ω=0.9 时,得到更高的能量效率。 图3 不同优化指标下系统能量效率与最大发射功率的关系 在图4 中,比较了全面学习粒子群算法和原始粒子群算法在不同惯性权重ω下的系统能量效率。从图中可以看出,系统能量效率随着迭代次数的增加而增加,并且当惯性权重ω=0.5 时算法的收敛性最好。且在相同的迭代次数下,全面学习粒子群算法可以得到更优的能量效率。 图4 粒子群算法在不同惯性权重下对能量效率的影响 本文在NOMA 下行链路系统中,以提升系统能量效率为优化目标,提出了采用全面学习粒子群算法进行功率分配。所提方法在满足用户最低速率要求的前提下提升系统能量效率,并且保证频谱效率。仿真结果表明,在相同的频谱效率条件下,本文所提方案比采用原始粒子群算法和文献[13]算法进行功率分配具有更高的能量效率,并且得到了更好的收敛性。通过本文所提方案实现系统能量效率优化,有效提升了资源利用率,减少了资源浪费。进一步研究将继续深入对过程进行自适应调整,使算法更加智能化。
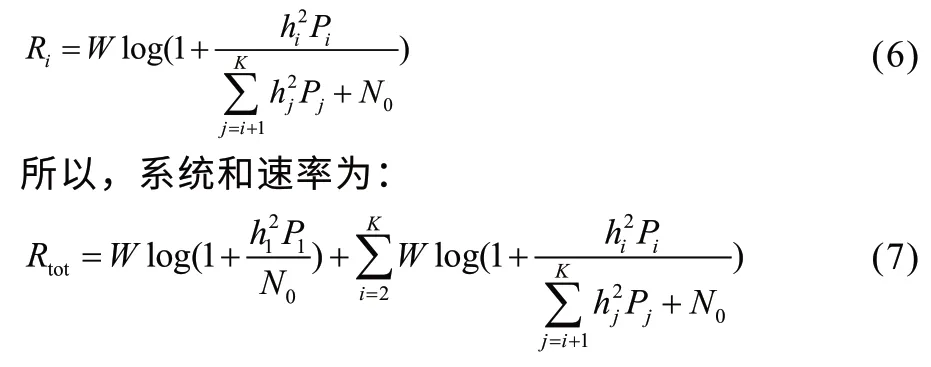
2 NOMA下行链路能效模型及优化问题

3 基于全面学习粒子群算法的功率分配方案
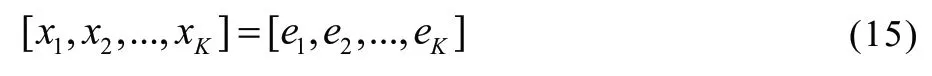
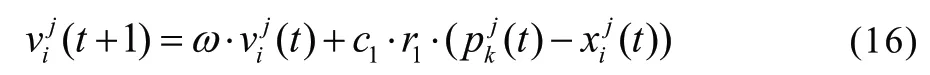


4 仿真分析


5 结束语
