多假目标干扰样式的干扰效果分析

叶锴，徐筱波，王登峰

（中国船舶重工集团公司第七二三研究所，江苏扬州，225001）

0 引言

在探测敌方雷达电磁信息并对其进行破坏的过程中，多假目标干扰作为一种常见的干扰方式，受到广泛关注。多假目标进行干扰的方式是干扰机发射与目标回波信号相仿的多假目标信号，跟随目标回波信号一起输入进雷达接收机[1]，影响敌方对真实目标的探测与跟踪，让雷达很难从这些假目标的里面分辨出真实的目标信号，甚至可能使雷达信号处理机处理回波时出现过载或饱和的现象，从而达到隐蔽真实数据的效果。又因为在进行干扰的时候大部分使用的是数字储频的方法，对雷达信号拦截后再复制延时转发，能够在很大程度上地减少干扰的功率[2]，增加干扰可能性，所以多假目标干扰的技术在干扰机里的应用也是越来越常见。

国内外对多假目标干扰的干扰样式和干扰特征开展过诸多研究。例如卷积相干干扰、类杂波干扰等，而当下对于该干扰样式效果的研究大都只考虑的是由于多假目标的出现，导致干扰效果增强，会使得检测门限抬高从而增加检测难度，但没有考虑到由于假目标间隔、幅度等的差异所导致检测门限不同、假目标数量增加甚至会致使干扰效果出现下降的情况[3]，由此可见，对于多假目标干扰的研究还不够透彻，对于多假目标干扰在干扰效果不稳定的定量分析是少之又少，没有仿真研究干扰效果随多假目标间隔的影响。因此本文将要借助恒虚警检测，从多假目标的形成机理，再通过恒虚警检测后的干扰效果的变化，对多假目标的干扰效果展开深入研究，并依靠仿真分析加以验证，从而分析出多假目标间距对干扰效果的影响。

1 多假目标的形成

1.1 干扰信号的产生

多假目标干扰的原理是通过形成遮蔽式干扰来压制真实目标信号，其产生方法总结起来主要有以下3种：

(1)使用存储转发。干扰机在截获雷达发射的完整信号后，开始对该信号采取复制延时转发的方式，当转发结束后再复制发送下一个。如果使用这种干扰方式，当干扰雷达使用的信号脉宽较小时，便容易生成密集度较高的多假目标；不过，假如干扰雷达使用的信号脉宽较大，那么假目标之间的间隔会随着发射脉冲信号宽度的增加而增加，起不到很好的干扰作用[4]。

(2)通过截取部分脉冲进行干扰。干扰机在获得雷达脉冲的局部信号之后开始持续转发，假目标的间距是靠侦察到的雷达发射信号脉宽所确定[5]，当所侦察的信号脉宽很小时，假目标的脉宽也会随之变小，从而增加密度，解决了第一种方法无法对脉宽大的信号产生密集干扰的问题。但是该方法也有缺点，因为回发的假目标仅仅是所发射的雷达信号的一部分，即使能保证假目标信号的功率不发生改变，可因为假目标信号不适应雷达匹配滤波器，所以无法得到雷达进行信号处理后的全部增益，所以假目标信号到达雷达系统后，并没有获取到雷达信号处理所需的全部功率，可能会使得假目标信号有一定程度的浪费。

(3)采用复制叠加干扰。将已复制的假目标信号进行时域延时并相互叠加，假目标信号进入雷达后再进行脉冲压缩处理，这时便会将脉冲宽度变小，此时形成的假目标会较为密集，密集程度是通过复制的脉冲信号间的时延所确定[6]。而因为干扰机所提供的发射功率是固定的，那么在时域上进行叠加的时候，每个假目标功率都仅为干扰机功率的一部分，所以假目标的功率会相对减少[7]。

本文采用复制叠加干扰方式，首先设定雷达的发射回波信号是线性调频（LFM）信号，记为下式：

式中:f0为载频；为调频斜率，其中Bw指信号带宽，wP指信号脉宽。

假定采样周期为sT，则采样信号的波形函数可表示成：

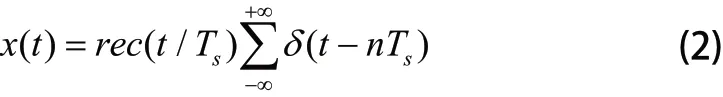
干扰机在给雷达回波信号进行采样后传送信号，其中采样的信号为：

由此可得该信号经脉冲压缩后的结果如下式所示：

式中，y(t)代表的是初始雷达发射信号通过脉冲压缩后得到的输出。根据上式中能够得知，干扰信号在进行脉冲压缩后的第一项与初始回波信号完全相同，唯一不一样的地方是幅度转换成原来信号幅度的τ/Ts倍[8]。

在采样雷达信号后，干扰机转发采样后的信号，每次采样后再转发，可以一次，也能够多次，即所谓的复制转发，次数的最大值为N=T s/τ−1。如果 N 是整数，则干扰机能够实现 N 次完整转发[9]; 如果 N 不是整数的情况，那么最后一次转发只能转发局部的采样信号。当发送该信号后，这时转发的假目标信号与真实回波信号有一定延时，能够使得回波信号的前后出现假目标串，然后再对采样信号进行正弦加权调频，此时转发的信号为：

式中：mf=k fma/Ω为调频系数。

由此可知，干扰信号可表示成：

1.2 干扰信号的频域特性

干扰信号的频谱表达式一般由下式所示：

式中:J(f)、S2(f)和Q(f)分别为j(t)、s2(t)和q(t)的频谱。

针对转发的信号s1(t)，当其通过脉冲压缩后所形成的信号幅值如下式：

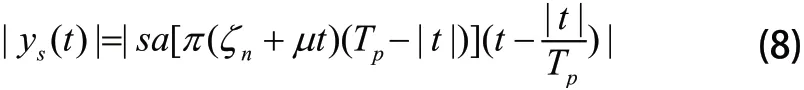
式中：ξn=nfs。在t的值取t=−ξ n/µ时达到最大值。相邻最值之间的间隔时间记作：

正弦加权后的信号q(t)的调制信号n(t) =asin Ωt具有周期性，如果t所代表的持续时间是无穷大的情况[10]，那么使用贝塞尔函数便可以把它变为如下形式：

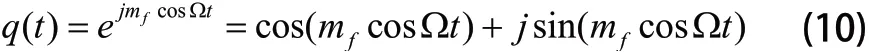
可进一步转化为：

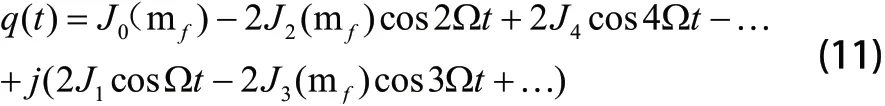
由式（11）可见：q(t)为间隔频率取Ω的正弦波构成，其幅度与贝塞尔函数值J s(mf)有关，对J s(mf)来说，对于某固定mf，当n>mf+1时，J s(mf)≈0，脉冲干扰有效的数目约等于转发信号2mf。

转发信号s2(t)的频谱为，进行正弦调频后的信号频谱是那么干扰信号频谱可表示成：

由此可知，采样后的正弦加权调频干扰就可以理解为在生成的假目标信号前后再对称产生了多个假目标，这个数目约为2mf[11]。间歇采样转发干扰所生成的假目标间距为：f s/µ，正弦加权调频干扰所生成的假目标的间距可表示为∆tsin=fsin/µ。

2 恒虚警检测设置

如果想要将发现概率增大，那么根据干扰、杂波等因素，可以考虑使用恒虚警检测器，恒虚警检测器是种类很多，其中比较常见的恒虚警检测器包含单元平均取小（SO-CFAR）恒虚警检测器、单元平均恒虚警检测器（CA-CFAR）和单元平均取大恒虚警检测器（GO-CFAR）这三种情况，三种检测器在增大检测概率上有着不一样的效果。

如图1所示，这是恒虚警预警器的示意图，假设单元数一共为N个，中间的为被测试单元，被测试单元左右紧挨着的是保护单元，数目为两个，被测单元左边（包括保护单元）为左侧假目标，其能量的平均值用表示，其中；被测单元右边（包括保护单元）为右侧的假目标，其能量的平均值用表示，其中那么可以把CA-CFAR、GO-CFAR与SO-CFAR这三种单元平均恒虚警检测器的检测门限则可以用式（13）、（14）、（15)所示：

图1 恒虚警检测器示意图

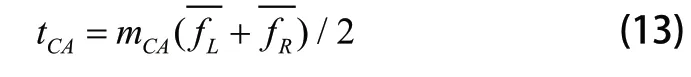
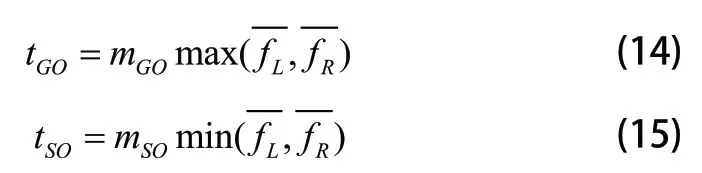
式中：mCA、mGO和mSO是单元平均检测器、单元平均取大检测器、单元平均取小检测器的乘性因子。

干扰机获取目标回波信号之后通过复制、幅度调频等处理后，产生很多和目标信号近似的假目标信号，导致雷达很难发现真实目标位置。在多假目标的影响后，当恒虚警检测器的参考单元里面出现出现假目标时，就能够改变雷达恒虚警检测门限，从而影响雷达对于真实目标的探测。

由式13到15所知：在多假目标恒虚警检测中的影响因素主要有两个，一个是被检测目标两边假目标参考单元的能量大小，另一个则是恒虚警检测器的乘性因子取值。这两个因素的取值，将会直接影响目标检测的效果。

如果将假目标之间相隔的距离设为∆dj，守卫单元个数为2个，那么恒虚警检测器的长度大小便可以表示成为L=（2N+3）∆dr，∆dr为检测的参考单元距离，那么恒虚警检测器参考窗内的假目标平均数量为

在m＜1时，如图2所示，拖动恒虚警检测器的参考窗，恒虚警检测器里并不会包括假目标，而在真、假目标之间的距离大于N∆dr的时候，恒虚警检测参考窗里也不包含假目标，此时恒虚警检测门限VCA、VGO和VSO不会受到影响。而当真、假目标间隔取值小于N∆dr时，恒虚警检测参考窗里仅剩1个假目标，此时VCA和VGO受到假目标的干扰。

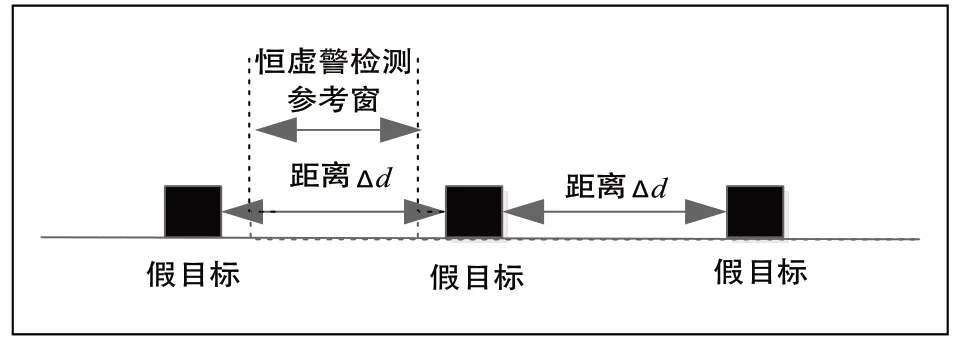
图2 m<1时的参考窗与假目标关系

在1≤m<2时，如图3所示，即假目标间隔长度超过参考窗长度的一半却没有达到一个参考窗长度时，那么无论恒虚警检测器的参考窗在哪里，均有起码1个假目标落入参考窗内，此时，检测门限tCA、tGO和tSO都被影响。

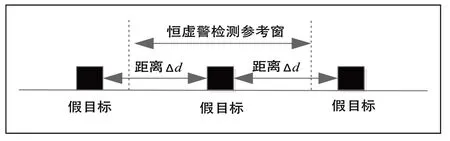
图3 1≤m<2时的参考窗与假目标关系

在m≥2时，如图4所示，无论恒虚警检测器的参考窗处于什么位置，都有至少1个假目标各落入恒虚警检测器的参考窗左右相隔的参考单元中，此时的检测门限将会受到假目标的影响。

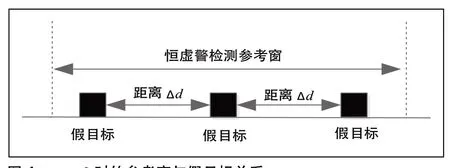
图4 m≥2时的参考窗与假目标关系

2.1 检测器的乘性因子对检测门限的影响

针对不同用途的雷达，所对应的虚警概率不同，导致乘性因子m的数值会发生变化，检测门限变化大小也随之改变。例如如果雷达是用于跟踪制导，则需要降低检测门限从而获得较高的发现概率，这时乘性因子m的取值也便随之而增加。以单元平均恒虚警检测器为例，乘性因子mCA的表达式如下：

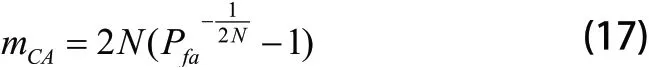
式（17）中：Pfa代表的是虚警概率。乘性因子取值不同，检测器的输出量也会变化。例如针对左右两侧参考单元个数等于N/2时的 CA-CFAR检测器来讲，由式（16）便能计算到当虚警概率不一样时的乘性因子数值。假设N=20，则Pfa数值取10-4、10-6、10-8时，可以求到乘性因子mCA的数值分别等于10.36、16.50、23.40，而虚警概率的大幅变化会导致检测门限随之变化。虚警率的值越小，检测门限的取值则越大。

2.2 CFAR检测下的多假目标干扰效果

由上所述，多假目标恒虚警检测下的干扰效果跟假目标本身的能量以及雷达的检测门限和虚警概率有关。在以上参数发生改变时，干扰效果也会不一样。

在m≪1时，由于是多假目标稀疏分布。这时的假目标就会取代真目标信号，显示在雷达终端设备中，此时的假目标在通过逼真调制后便能够形成欺骗干扰的作用。

在m<1时，假目标间隔超过恒虚警检测器参考窗大小，真假目标混合在一块。如果真假目标处于不同的恒虚警检测器，那么真假目标均会被检测到；如果真假目标落入同一个恒虚警检测器，假目标对雷达探测目标会产生影响。

在1≤m<2时，假目标会分散在各个检测窗里。因为每一个假目标的信号功率远远大于噪声功率，所以当检测器内不包括真实目标时，每个假目标都可以被检测，从而形成干扰效果。在检测真实目标信号的时候，将检测门限用t=mpj/2N表示，其中m为乘性因子，pj为假目标能量的值，处在相同参考窗内的真假目标之间会发生遮蔽现象。当干扰效果较强，出现检测门限超过目标回波信号能量时，雷达将检测不到真实目标；当干扰效果较弱时，此时检测门限V小于真目标信号能量，真目标混在假目标中，难以分辨。

当m≥2时，在恒虚警检测窗里将有至少2个假目标。检测门限也可以简单表示为V=knxj/2N，其中n为检测窗内的假目标个数。当检测门限的值超过目标回波信号能量时，雷达则探测不到目标实际信号。并且在探测假目标时，检测窗内假目标之间也会互相影响，而如果检测门限数值超过被探测的假目标能量，假目标便会出现自遮蔽现象，雷达此时也无法发现假目标；此时，根据V>xj，推出kn>2N；以单元平均恒虚警检测为例，由推出当N＝10和n＝2时，得到假目标出现自遮蔽的虚警概率约为0.95* 10−6；当n＞1，此时假目标密集程度更高，这时假目标出现自遮蔽的概率也变得更大。因为干扰机发射的功率要分摊到多个假目标里，所以假目标数量越多，每个单独假目标的功率就会越小，通过CFAR处理后，只有当信号大于检测门限值时，真实的回波信号才会被雷达发现，所以如果干扰信号较弱、真目标信号又大于检测门限数值并且检测门限V大于假目标能量xj，这时在假目标自遮蔽效应的影响下，没有产生明显的干扰，很难影响雷达对目标实际回波信号的探测。这也就解释了为什么会出现多假目标干扰效果反而比单个假目标干扰效果差的原因。

3 仿真与分析

为了更好验证假设，通过MATLAB仿真进行验证，程序流程图如图5所示。

图5 程序流程图

具体流程是先假设雷达发射信号的脉宽是25μs，带宽是20MHz，采样率是2.4GHz，脉冲重复周期是200μs，信噪比取15dB，然后根据设置的参数生成一个线性调频信号，之后再对信号进行脉冲压缩，然后采用复制转发的方式加入多假目标，最后使用蒙特卡洛采样，结合单元平均恒虚警检测，假设参考单元数目是20，恒虚警率为10-6，对真、假目标混合后的信号进行区分检测。得到的情况如下：

(1)在未加入干扰信号时，目标回波信号经脉冲压缩后的图像如图6所示，此时雷达检测概率如图7所示，当信噪比为15dB时，雷达检测概率约为0.88。

图6 真实目标脉冲压缩后的信号

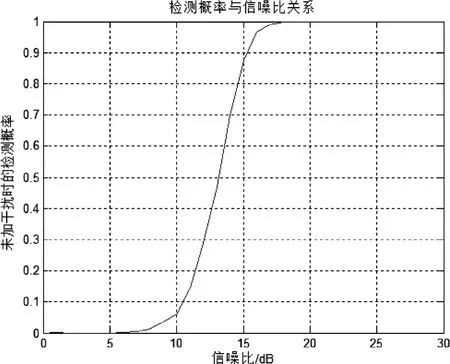
图7 无干扰下的检测概率与信噪比关系

(2)当加入干扰信号且信噪比固定为100dB，当假目标稀疏时，蒙特卡洛采样次数为1000次，经过脉冲压缩后的干扰机发射的干扰信号与真实信号的关系由图8可见，从图中可以看出：此时单个假目标与真实回波信号信号幅度相同，而在多假目标压制下，可以对真目标可以完成压制效果。通过图9可以看出：当信噪比为15dB时，此时雷达的检测概率约为0.75，与未加干扰时有明显下降。

图8 干扰机发射的干扰信号与真实信号的关系

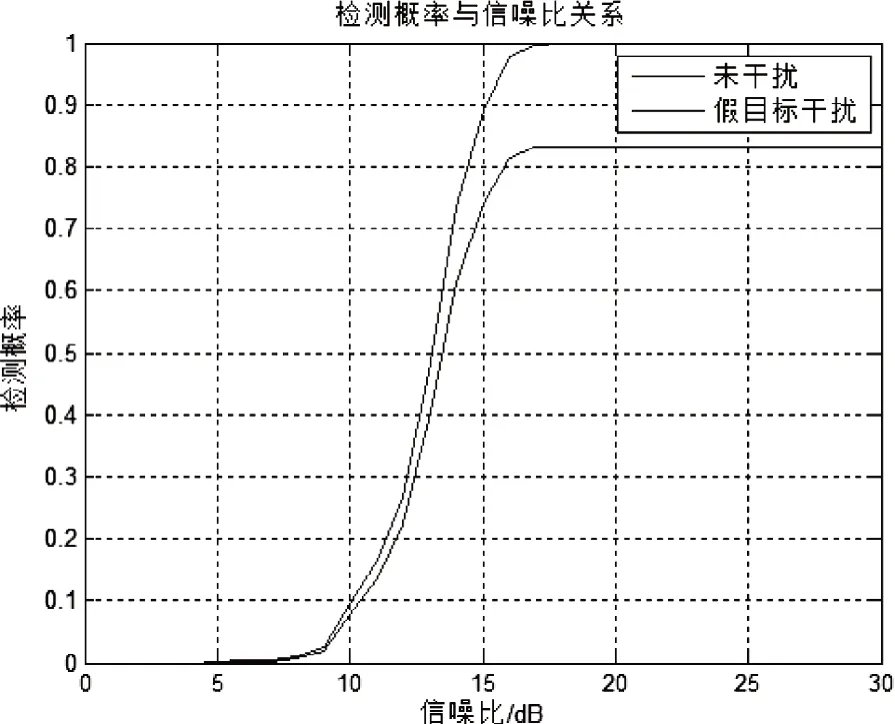
图9 稀疏假目标干扰下的检测概率与信噪比关系

(3)当加入干扰信号且信噪比固定为100dB，假目标过于密集时，假目标功率也随之降低，经过脉冲压缩后的干扰机发射的干扰信号与真实信号的关系由图10可见，由图可见：此时假目标功率低于真实目标功率，脉宽大幅减小，小于真实目标信号脉宽，起不到压制目标信号的效果，再观察雷达检测概率，在信噪比为15dB时，检测概率与未加干扰时没有发生太大差异，假目标干扰不明显（见图11）。

图10 干扰机发射的干扰信号与真实信号的关系

图11 密集假目标干扰下的检测概率与信噪比关系

4 结论

根据恒虚警检测下的多假目标之间间隔的不同，通过理论加仿真分析，比较出多假目标干扰样式在不同间隔时干扰效果的差异，通过本文的理论推算，结合仿真分析后能够发现，当开始多假目标干扰的时候，可以通过被干扰雷达的恒虚警检测参数对假目标间隔进行修正。当假目标数量增加且间距过小时，会使得单个假目标的干扰功率减少，甚至出现压制不住目标信号的情况，没有起到降低雷达的发现概率的作用。因此为了获得较好的干扰效能，应当适当调整假目标间隔的大小，使得检测门限抬高的同时又不会使得假目标干扰功率下降太快，从而达到干扰雷达侦察的效果，为提高多假目标的干扰效能提供更加合理的支撑。