南沙群岛永暑礁西南部珊瑚礁动力稳定性分析评价

赵文燕，王桂萱,2，尹训强,2，赵 杰

(大连大学 土木工程技术研究与开发中心，辽宁 大连 116622)

珊瑚礁主要由霰石、镁方解石和碳酸钙组成，其中碳酸钙含量高达约96%，是珊瑚群体死后经过长期的地质作用演化形成的土体。在岩土地质学中，其被认为是一种特殊的岩土类型。

珊瑚礁在许多工程中都得到应用。自20世纪40年代起陆续引起关注，澳大利亚和美国利用珊瑚礁在太平洋岛屿上修建了高速公路和机场跑道，据报道这些设施使用至今[1]；在伊朗波斯湾附近首次发现与近海石油平台稳定性有关的岩土工程问题。然而，当时这些问题并没有引起关注；20世纪末，珊瑚礁建设方面的问题被广泛报道，引起了人们的关注，并开始对珊瑚礁的力学特性进行研究[2]。尽管在陆地边坡、隧道及核电等方面的稳定性已经进行了大量的研究[3-5]，但对珊瑚礁地层的稳定性和机制仍知之甚少。随着现代深海渔业、海洋能源、海底油气资源的开发以及旅游、交通和国防事业的发展，珊瑚岛礁的建设在我国具有极其重要的战略意义和经济价值，为了满足珊瑚岛礁技术建设的需要，针对珊瑚岛礁的场地稳定性、液化特性及岩体结构等相关问题的研究已迫在眉睫。国内许多学者展开研究并取得一些成果。胡进军等[6]对典型岛礁场地地震效应进行了初探，考虑礁岩构造和海水对岛礁场地地震反应分析的影响；陈国兴等[7]针对饱和珊瑚砂进行循环加载实验，发现了围压和相对密度对珊瑚砂液化特性影响的规律；邵广彪等[8]针对地震液化分析了海底液化震害特点，指出液化研究中的不足；李建波等[9]对层状土动力分析进行了等价线性化分析研究。

文中以永暑礁西南部珊瑚礁为工程背景，对其进行数值模拟，对土体进行等价线性化处理，从稳定安全系数、动力加速度响应及液化特性3个方面分析珊瑚礁的稳定性。

1 工程概况

永暑礁西南部礁体稳定性从宏观角度来看，其没有断层活动通过，属于区域地壳稳定性较好地区。永暑礁[10]坐落于南海诸岛的中部(9°32′N—9°42′N, 112°52′N—113°04′E)，是一种开放式环礁。如图1所示，礁顶顶部呈橄榄形，长轴为NEE—SWW走向，长度约为25 km，短轴为NW—SE走向，宽度约为6 km，面积约为110 km2。礁顶的中部为开放式泻湖，面积约为105 km2，水深20～30 m。永暑礁表层由疏松的生物砂石组成，表层以下是礁灰岩，礁体呈现“岩盆结构”。

图1 永暑礁平面图Fig.1 Plan map of Yongshu Reef

根据工程地质和勘探资料[11]对南海永暑礁的礁体形态和地貌进行分析，收集了永暑礁西南部珊瑚礁的地质相关数据，做出永暑礁工程地质的剖面图，如图2所示， 其显示珊瑚礁地层在横向上具有明显的带状分布特点，永署礁地层由五层组成[12]即块状砾石、砂砾、中粗砂、粉细砂和礁灰岩。珊瑚礁方面的研究之所以能够发展迅速，由于它的出现解决了陆地不足和高额的建设成本问题，就地取材，将其作为理想的填筑材料。然而，鉴于珊瑚岛礁海洋工程地质体及钙质砂易碎等特殊的动力力学特性，其在复杂海域环境下珊瑚岛礁的抗震安全分析问题需亟待解决。

由于珊瑚岛礁中钙质砂易碎性、考虑土体的非线性特征，需要对土体进行等价线性化处理，通过数值模拟计算，根据不同情况下的计算结果来分析评价珊瑚礁的抗震安全性，从而得出揭示礁坡的地层构造、地形和位置以及珊瑚砂的物理特性对珊瑚礁稳定安全系数、动力加速度响应及液化特性的影响规律。

2 岛礁抗震稳定性分析计算模型

2.1 珊瑚岛礁有限元模型

计算模型采用二维模型，如图3所示。珊瑚礁从表面到底部有大量的块状砂石、砂砾、中粗砂、粉细砂和礁灰岩。岛礁模型主体部分长274 m，在场地与结构的相互作用计算中，根据经验可知，场地的计算边界宜取结构基础宽度一半的5倍。因此，本文将岛礁模型底部基岩延伸至685 m。整个轮廓可以分为2 519个节点和2 194个单元，最大网格尺寸为2 m。

图3 永署礁有限元模型Fig.3 Finite element model of Yongshu Reef

2.2 材料本构

珊瑚礁动力本构模型及相关参数的确定是珊瑚岛礁场地地震反应分析的前提和基础。本文根据陈国兴等[12]通过动三轴试验得出的珊瑚岛礁试验数据并提出的一种适用于珊瑚礁的修正Matasovic本构模型进行分析，并通过不同围压下的相对密度验证了该本构模型的合理性。具体的剪切模量G/Gmax和阻尼比D与剪应变幅值的关系，如图4(a)所示。

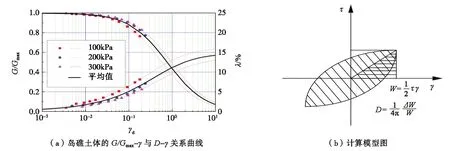
图4 本构曲线及模型Fig.4 Constitutive curve and model

该本构模型中应力-应变关系如下：

(1)

其中剪切模量可以表示为：

(2)

式中，G0为初始时刻土体的最大剪切模量；γγ为参考剪应变；β，s为描述珊瑚礁初始骨架曲线形状的系数。

永署礁西南部珊瑚礁在地震作用下的稳定性与土的动力特性密切相关。众所周知，土体是一种非线性很强的材料，土体的参数多，计算复杂，采用传统的非线性时程分析方法难以控制。Seed[13]首次提出了等价线性化的概念，简化其在地震荷载作用下土体的非线性响应，将土体假定成粘弹性，将土体的剪切模量G定义为所有滞回圈的平均斜率，而土体的滞回圈的面积即能量的耗散作为阻尼比D，用此方法来研究土体的非线性特征，如图4(b)所示。等价线性化分析最大的优点在于能充分考虑土体在地震作用下的非线性及复杂性，计算思路清晰且难度低，计算结果的准确性能够满足工程中的需求。此外，该方法还能大大提高计算效率。

在等价线性分析方法中，通常需要试验确定土体材料的最大(初始)剪切模量G0，其计算公式如下：

(3)

(4)

等效剪应变振幅用于确定剪切模量及阻尼比，由于初始等效剪应变振幅大小未知，因此必须由迭代来确定。目前，进行等价线性法计算主要结合波动问题的频域求解过程。

2.3 计算输入

2.3.1 地震波选择及波浪荷载输入

目前我国在南海尚未设置专门强震检测系统，因此缺乏对南海地震的实测记录。由于南海和日本都处于环太平洋地震带，地址条件相似。因此，为了考虑震级、频率等因素的影响，本文选取的地震动记录来源于与日本东京湾在PGA及持时相似的人造波，其具体的加速度时程如图5所示。

另外海浪能对珊瑚岛礁也有较大的影响[14]，因此加入波浪作用，采用的波浪荷载周期为4.5 s，作用时间为25 s，如图5(c)所示，但是在分析中不考虑波距和波深的影响，因此，将波浪荷载简化成与时间相关的切向边界应力。

图5 时程曲线Fig.5 Time history curve

2.3.2 计算参数

由于珊瑚礁特殊的物理力学性质，其颗粒与一般的陆源砂有显著的差异，文中所用的物理力学参数见表1。

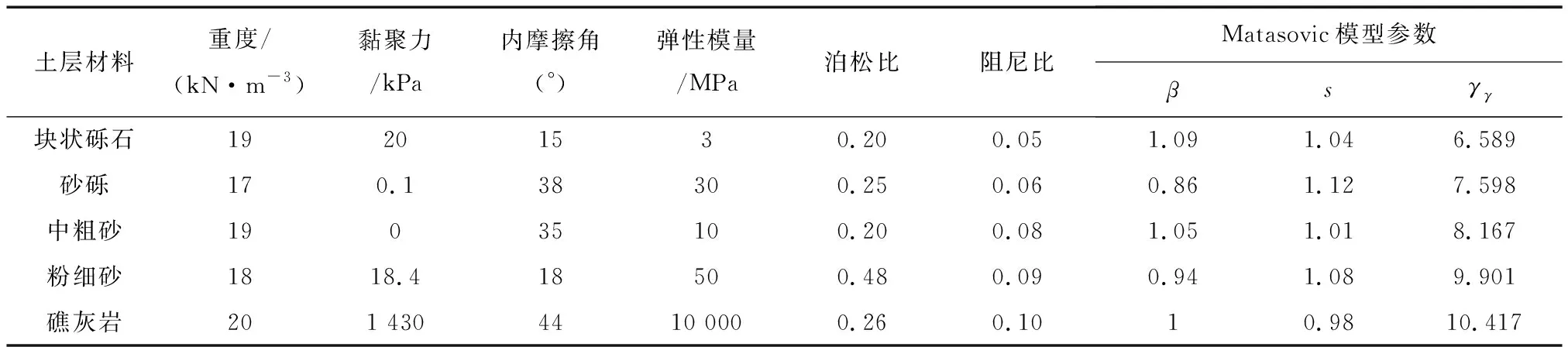
表1 珊瑚礁地层物理力学参数Table 1 Physical and mechanical parameters of coral reef strata

3 永暑礁西南部珊瑚礁抗震稳定性分析

3.1 稳定性分析

在静水压力和地震荷载作用下，采用滑动面法计算边坡稳定安全系数，其中将地震荷载简化为水平和竖直两个方向的不变加速度作用，进而转化为一种地震惯性力，最终确定最危险滑动面。数值计算结果如图6所示：内礁坡安全系数为1.1，外礁坡安全系数为8.491。表明珊瑚礁两侧较稳定，但珊瑚礁两侧的安全系数相差显著，外礁坡比内礁坡安全的多。其主要原因可能是外礁坡珊瑚礁具有天然的生物礁结构，结构稳定性好，而泻湖附近的内礁坡生物礁呈粉细砂质非胶结结构，结构的稳定性较差。

图6 永署礁滑动面Fig.6 Yongshu Reef sliding surface

动力有限元分析中考虑波浪荷载并将其简化为与时间相关的切向边界应力，如图7所示，不考虑波浪场与土体表面之间的相互作用，把波浪荷载都作为外部荷载单独施加到土体表面。

图7 波浪荷载示意图Fig.7 Schematic diagram of wave load

采用有限元动力时程分析方法，其是计算每一个时刻结构下的稳定性安全系数，考虑在地震过程中珊瑚礁结构应力的瞬时变化，另外，该方法还充分考虑了土体材料的非线性和不均匀性。我国在海工建筑物方面的相关规范中均采用此方法进行抗震稳定性评价分析。何江达等[15]计算分析了每个单元节点的应力分布和变形情况；赵杰等[16]运用有限元动力时程法计算导流堤的最小安全系数来分析其稳定性。因此，采用此方法分析珊瑚岛礁结构，并把最小安全系数作为评价岛礁稳定性的标准。

利用有限元计算土体中各个单元高斯点在每一时间点的动应力变化，与静应力场叠加并分析结构的动力稳定性，具体的安全系数计算如下：

(5)

式中ci、φi分别为第i个单元土体的粘聚力、内摩擦角；li表示第i个单元滑弧的长度；σni、τni分别表示为第i个单元滑弧面上法向应力、切向应力。

在地震和波浪荷载作用下，计算得到的最危险滑动面，如图8所示。内礁坡的安全系数约为0.6～1.8，而靠近海一侧的外礁坡安全系数约为1.8～4.2。得出安全系数随时间变化过程，如图9所示，安全系数内礁坡比外礁坡更小，相较于外礁坡更危险，需采取一些必要的加固措施。

图8 内外坡最危险滑动面Fig.8 The most dangerous sliding surface of inner and outer slope

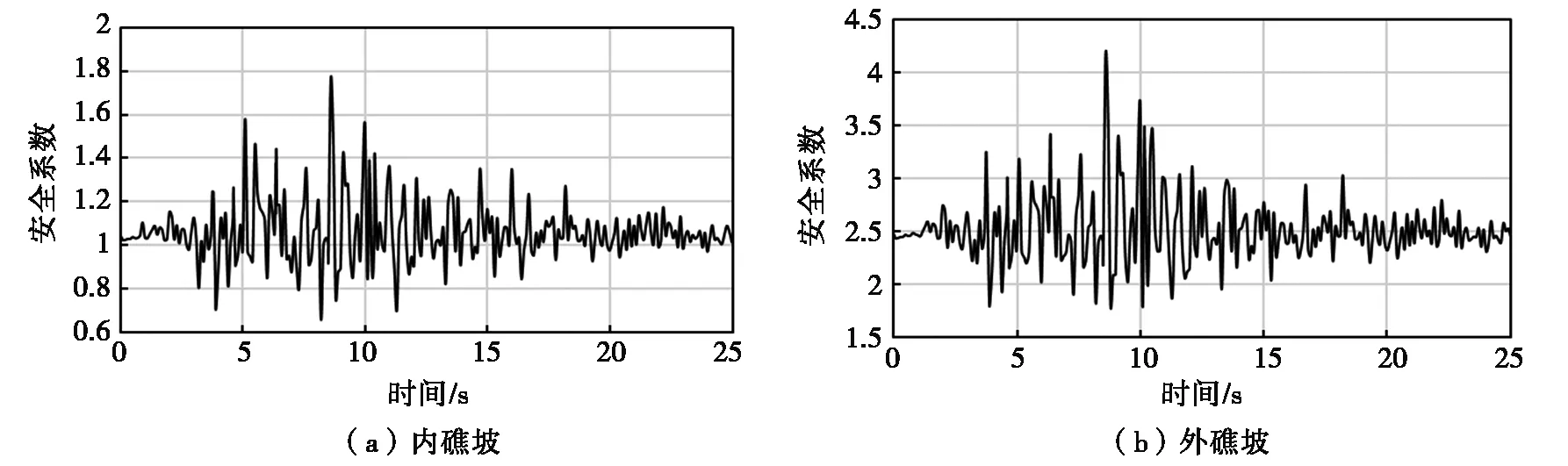
图9 动力安全时程曲线图Fig.9 Dynamic safety time history curve

3.2 加速度响应分析

考虑地震和波浪荷载作用，计算结果如图10所示，由于土层厚度不均，其动力效应有所不同；同时，土的特性也不同且上层有砂土和黏土，不同监测点的加速度响应和放大规律存在一定的差异。给出了不同方向的加速度响应分布情况：珊瑚岛礁水平方向加速度的最大放大倍数为6.67，竖直方向加速度的最大放大倍数为3。

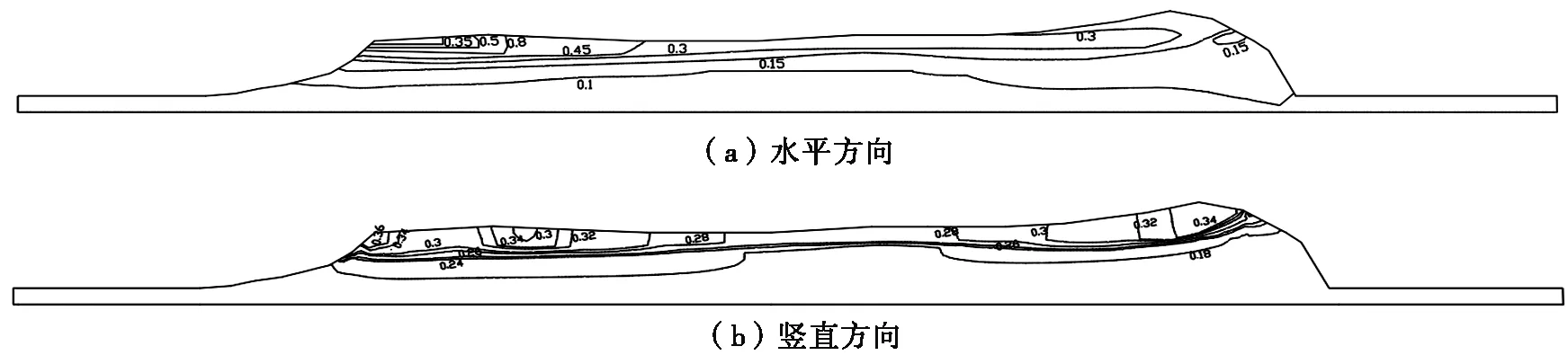
图10 最大加速度响应Fig.10 The maximum acceleration response

为了探究珊瑚岛礁内部的加速度的响应过程，在内部的土层分界面上设置6个监测点，输入同一种不同峰值的地震波，针对岛礁PGA放大系数进行分析，具体监测点的位置如图11(a)所示。通过计算监测其放大过程分析峰值加速度的变化情况。分析结果得到的规律如图11(b)：(1)整体上，随着输入地震动峰值的增大水平向PGA放大系数呈逐渐减小的趋势，主要可能是因为输入的地震动幅值越大，土层产生的剪应变越大，进而剪切模量减小，土体的强度降低，最终使PGA放大系数减小；(2)局部上，珊瑚岛礁的加速度在-2 m附近有转折，在此PGA放大系数存在临界点，原因可能是临近地表处土层剪应变较大，导致剪切模量减小，土层出现了软化的趋势，从而PGA放大系数有所减小；(3)岛礁内部结构的PGA放大系数自下而上两个方向都随着高程的增加而减弱，最终基本稳定在1左右；(4)输入同一种不同峰值的地震波对岛礁在不同监测点的加速度放大效应存在着显著差异，这可能与地形和位置有关。在地震波和波浪荷载的共同作用下，随其强度的变化土体的非线性也随之改变。由此可推断，珊瑚岛礁的加速度响应及相应的分布规律不仅与受到的地震波和波浪荷载的影响，也可能与土层的厚度及土层种类特性有关。

3.3 液化特性分析

在液化动力分析中，大多都采用总应力法，但是没有考虑孔隙水压力和有效应力对剪切模量产生的影响。因此，有效应力法[17]相比较于总应力法更合理准确。本文采用有效应力法对砂土层进行液化特性分析。

有效应力法中液化的土体有效应力为零，采用孔隙水压力-应变模型，求出孔隙水压力，进而求出对应下的有效应力。有效应力是零的液化单元相连成了液化区。采用有效应力法中的孔压-应变模型，具体理论如下：

(6)

Δεvd为累积体积应变，γ为剪应变，c1、c2、c3、c4分别为排水周期剪切试验确定的试验参数。

(7)

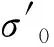
永署礁地层结构中存在不同厚度的砂土层，在地震及波浪荷载作用下采用上述方法进行液化分析，取c1=0.70、c2=0.61、c3=0.22、c4=0.50，给出珊瑚砂循环次数和体应变关系，如图12(a)所示。计算出每个时间段孔隙水压力的增量，得出每个时段结束时的累计孔压，最终求出单元时段的有效应力，得出有效应力为零的液化单元。计算结果如图12(b)所示。整体来看，由于砂土的特性，结构的整体刚度低，在地震及波浪荷载作用下，中粗砂和粉细砂层液化带范围较大，液化程度较严重。内礁坡液化区域远大于外礁坡的液化区域。

图12 液化分析Fig.12 Liquefaction analysis

4 结论

以永暑礁西南部珊瑚礁为研究对象，开展了强震及波浪等荷载作用下的静动力联合分析，具体分析得出的结论如下：

(1)在地震及波浪荷载作用下，从安全系数随时间变化可以看出，外礁坡在静水压力、地震及波浪条件下都是稳定安全的；然而，内礁坡可能会发生滑坡等失稳现象，这可能归因于内外礁坡的地层构造。

(2)整体来看，随着输入地震动峰值的增大，水平方向PGA放大系数呈逐渐减小的趋势；局部而言，珊瑚岛礁的加速度在-2 m附近有转折，此处的PGA放大系数存在临界点，原因可能是临近地表处土层剪应变较大，导致剪切模量减小，土层出现了软化的趋势，从而PGA放大系数有所减小；另外，岛礁内部结构的PGA放大系数自下而上两个方向都随着高程的增加而减弱，最终基本稳定在1左右；对于输入同一种不同峰值的地震波，针对岛礁在不同监测点的加速度放大效应存在着显著的差异，这可能与地形和位置有关。

(3)由于珊瑚砂的物理特性，结构的整体刚度低，在地震及波浪荷载作用下，局部中粗砂和粉细砂层液化带液化程度较明显，但相对岛礁整体液化程度小，不会影响岛礁的整体稳定性。

由上可知，基于有限元框架所建立的计算分析模型具有良好的合理可靠性，研究成果可为类似岛礁工程的抗震稳定性综合评价提供有益的参考。