旋转式无线充电系统偏移特性研究
2021-12-13程志远李东东邵会文
程志远 陈 坤 李东东 李 峥 邵会文
(上海电力大学电气工程学院 上海 200090)
0 引言
无线电能传输技术(Wireless Power Transfer,WPT)因其具有较高的安全性、灵活性和可靠性而被广泛应用于水下用电设备、生物医疗、电动汽车和无人机等各个领域[1-6]。
目前,作为人类探索海洋环境的重要水下设备——自动水下航行器(Autonomous Underwater Vehicles, AUV)普遍采用直接接触式传能方式,存在漏水、漏电等重大安全隐患。而无线电能传输技术因其采用非物理接触式实现能量传输,具有安全性高、环境适应性强等优点,可作为解决这一问题的有效手段[7-8]。典型的无线电能传输工作原理如图1 所示。交流电源经工频不控整流产生直流母线电压,后经逆变电路产生高频交流电,通过谐振网络由LCT 将能量传递至副边,最后经谐振补偿网络及高频整流环节实现负载供能。

图1 WPT 系统工作原理Fig.1 Working principle of WPT system
AUV 在水下进行无线充电过程中大多采用笼状对接系统,但由于水压与洋流的干扰可能发生轴向偏移[9],与充电装置之间的相对位置发生未对准的情况,进而对互感与耦合系数产生影响[10]。文献[11]研究了电动汽车上平面方形线圈横向偏移对互感的影响,并对线圈进行了抗横向偏移优化,同时采用串-串拓扑稳定系统输出。文献[12]为解决无线电能传输中由于线圈未对准而引起传输效率降低的问题,提出了一种太极线圈结构,通过与其他线圈对比,验证了太极线圈具有较高的抗偏移性。文献[13]设计了一种抗偏移性能优异的电动汽车用WPT 系统,该系统采用扁平螺线管的磁耦合结构,具有非常突出的抗横向偏移性能。但这两种结构用于AUV 在水下进行无线充电时兼容性较差,将提高建造成本。文献[14]提出了适用于动态无线充电的原边侧T 型补偿拓扑结构及参数设计方法,该补偿拓扑与设计方法具有在较大偏移范围内仍保持传输功率稳定的特性。目前,AUV 水下充电过程中需进行旋转对位,且容易发生旋转不对准的情况。故文献[15]提出了一种具有反向缠绕接收器并兼容AUV 外形的线圈结构,该结构在发射器线圈与接收器线圈之间发生旋转未对准的情况下,具有较为良好的传输性能。文献[16]提出了一种适用于AUV 水下充电的磁耦合结构——旋转式松耦合变压器 (Loosely Coupled transformer, LCT) 结构,该结构在不改变AUV 自身形状的前提下,实现灵活的机械对位,以相对较低的成本有效避免了旋转未对准的情况。但文中未对所提结构进行互感耦合的理论分析和偏移特性分析。然而互感耦合与偏移特性对于无线电能充电系统而言是十分重要的参数和特性,其会对系统的传输能力及传输效率产生影响,故本文对耦合系统的互感及偏移特性展开分析。
本文针对旋转LCT 发生轴向偏移对互感、自感、耦合系数、输出功率及传输效率产生的影响展开研究。首先给出了基于LCL_S 补偿结构WPT 系统输出功率与互感M的关系,并推导了旋转LCT的互感计算模型,在此基础上通过仿真对轴向偏移、副边线圈长度、互感、输出功率及效率之间的关系进行了分析,最后搭建一套WPT 样机对理论分析结果进行了实验验证。
1 WPT 系统建模与分析
1.1 旋转LCT 结构
旋转LCT 结构如图2 所示。原边侧铁氧体磁心在最外侧,副边铁氧体磁心在最内侧;副边线圈嵌套于原边侧线圈内。为了减少邻近效应与趋肤效应,原副边线圈均由利兹线绕制而成。该结构在不改变AUV 外形的条件下安装于AUV 外表面,且在AUV航行过程中不会造成额外阻力。

图2 旋转LCT 结构Fig.2 Rotary LCT structure
本文设计的笼状对接无线充电系统如图 3 所示。其中,LCT 原边侧部分安装于笼状对接装置,LCT 副边部分安装于AUV 中部。采用该种对接装置可使AUV 在水下无线充电过程中极大地避免了径向偏移情况的发生,LCT 副边安装于AUV 中部,有效地避免了传能过程中对AUV 前后端通信系统及高精度传感器等关键部件的电磁干扰。AUV 充电过程如下:当 AUV 需补充电能时,首先通过导航系统将AUV 引入笼状对接装置,同时发出充电信号,水下无线充电系统开始对AUV 进行电能补给。

图3 AUV 笼状对接无线充电系统Fig.3 AUV cage-like docking wireless power transfer system
1.2 LCL_S 型WPT 系统分析
图4 为本文所采用的基于旋转LCT 结构无线充电系统电路拓扑结构,其中UD为经工频不控整流转换的直流输入电源,S1、S2、S3、S4开关管构成H 桥高频逆变电路,Cp、Cs为原、副边谐振补偿电容,VD1、VD2、VD3、VD4为副边高频整流二极管,Cf为滤波电容,RL为负载,LCT 原、副边均采用圆筒磁心结构。
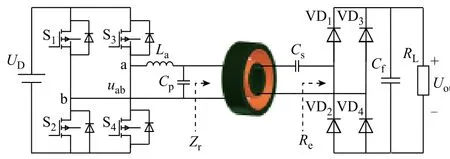
图4 系统拓扑Fig.4 System topology


式中,ω0为谐振角频率。根据电压与电流方程,可得出原、副边工作在谐振状态下各电流表达式为
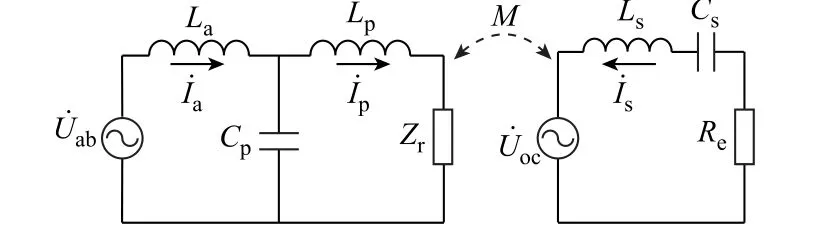
图5 LCL_S 型WPT 系统等效电路Fig.5 Equivalent circuit of LCL_S type WPT system
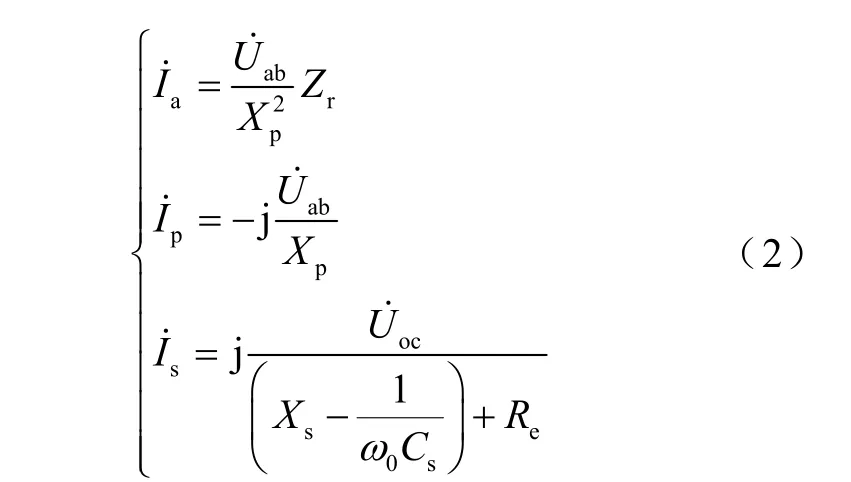
式中,Xp、Xs分别为原、副边电抗;Zr、Xp及Xs表达式为

对于副边采用串联补偿结构的WPT 系统,式(3)中的Re为

综合式(1)~式(4),可得到系统的输出功率Ps为
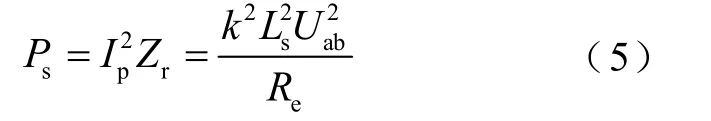
式中,k为耦合系数,表达式为

对于能量传输系统,效率是较为重要的参数,由文献[17]可得系统效率表达式为

从以上理论分析可知,互感M的变化会对无线电能传输系统中一些关键参数产生较大影响,如反映阻抗、耦合系数、效率及输出功率等,因此本文重点针对互感变化对系统传输性能的影响展开研究。
2 互感参数分析
图6 为载流圆线圈空间中任意一点磁场计算模型。载流圆线圈的圆心为坐标原点O;D(x,y,z)为磁场中任一点的坐标;D′(tcosα,tsinα,0)为D在xOy平面的竖直投影点;α为投影点到原点的连线与x轴的夹角;载流元Idl与x轴的夹角为β;i、j、k分别为x、y、z轴方向的单位向量。则dl为

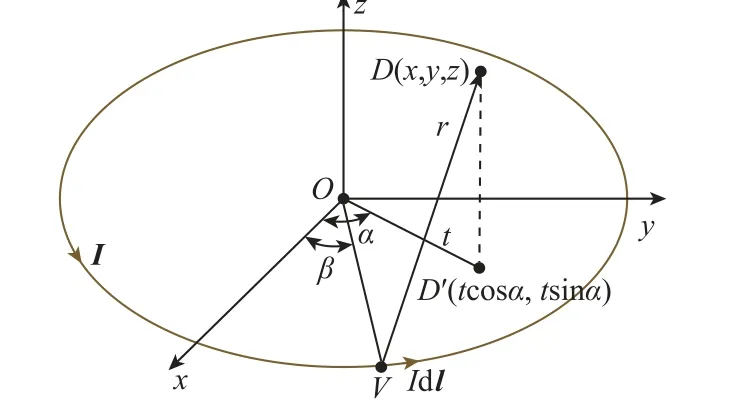
图6 载流圆线圈空间任一点磁场计算模型Fig.6 Calculation model of magnetic field at any point in current carrying circular coil space
Idl到P点的距离为

由于载流圆线圈的磁场强度仅存在径向分量与轴向分量[18],则
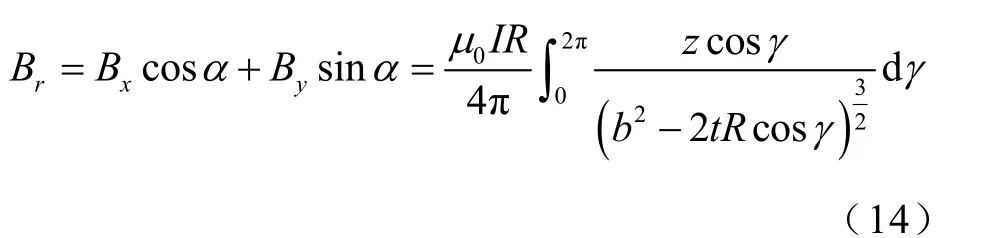
图7 所示为一个长为l1、半径为R1的载流密绕螺线管内部任一点磁场计算模型。本文所研究的原、副边线圈均为密绕线圈,故忽略其匝间距。线圈匝数为N1,电流为Ip,单位长度的匝数n1=N1/l1。由于螺线管中的磁场关于z轴对称[19],故本文可对螺线管内的一点磁场进行如下求解。
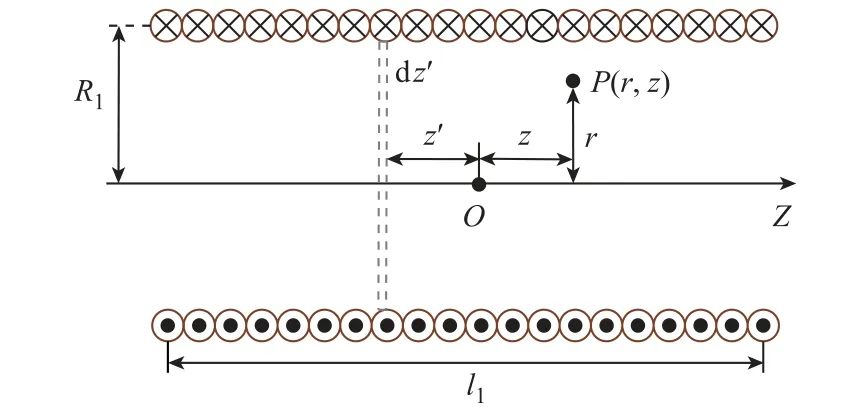
图7 载流螺线管内部任一点磁场计算模型Fig.7 Calculation model of magnetic field at any point in current carrying solenoid
r为P点到螺线管轴线的垂直距离;z为P点在坐标轴z上的投影点到坐标原点的距离;在螺线管上取一段长为dz′线圈元,匝数为n1,该段所通过的电流为Ipn1dz′,则由式(11)和式(12)可得

由式(16)可知,P点在螺线管线圈中的位置z发生变化时,轴向磁感应强度Bz的值将受到影响,同时r的改变将导致径向偏移。由于本文不对径向偏移进行分析,故仅考虑轴向偏移的变化对互感的影响。
互感可定义为

式中,ψm为接收线圈的磁通量;Ip为接收线圈的电流。将单匝接收线圈置于图7 所示螺线管内部,由于径向磁场将相互抵消,故其磁通量为

由式(20)、式(21)可得,M与原、副边线圈的半径、匝数、长度及其相对位置密切相关,且长度越长互感值越大。同时通过式(21)及式(16)可知,副边线圈在原边线圈内部的相对位置发生变化即z′-z的绝对值发生变化,Bz和Dr受到影响。结合式(20)可知,互感M将发生改变,具体变化情况将在第3 节进行分析。由文献[20-21]可知,铁氧体磁心可使线圈互感得到相应的改善,依据文献[4]所提仿真与曲线拟合的方法可确定铁氧体磁心系数kc,该系数与螺线管线圈互感之积即为旋转LCT 的互感值。
3 偏移特性分析
AUV 在水下充电过程中,由于受到强大的水压与暗流的影响,导致其与对接装置较容易发生轴向偏移,故本文将对多种不同情况的轴向偏移展开分析,为后续旋转式LCT 的开发与应用提供参考。由于AUV 充电系统中原边充电装置一般固定不变且改动难度较大,故本文在做仿真分析时仅改变副边磁心与线圈的长度,且各侧磁心与线圈均为等长,即齐平状态。
表1 为原边的仿真参数。表2 为副边的仿真参数,副边磁心外径均为48mm,磁心内径均为38mm,螺线管线圈半径均为 44.5mm,利兹线线径均为3.5mm。

表1 原边参数Tab.1 Primary side parameters
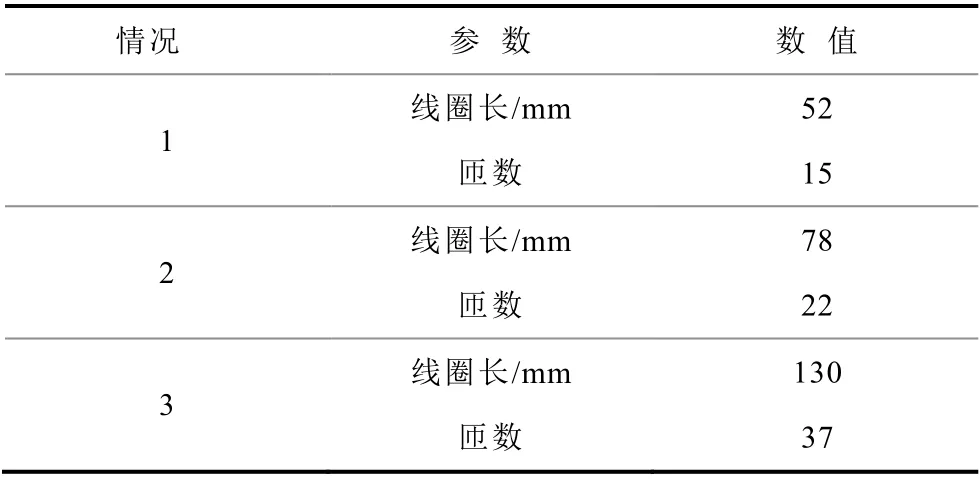
表2 副边参数Tab.2 Secondary side parameters
图8 为旋转LCT 轴向偏移示意图。图8 中轴向偏移距离L为旋转LCT 的副边线圈相对原边线圈较正对时轴向偏移出的距离。

图8 旋转LCT 轴向偏移示意图Fig.8 Schematic diagram of axial offset of rotary LCT
3.1 轴向偏移对互感的影响
下面将对三种不同副边长度的LCT 进行轴向偏移分析,观察在不同偏移状态下,旋转LCT 的互感与耦合系数的变化。
图9 为旋转LCT 副边长度为52mm 时,原、副边线圈互感、耦合系数与轴向偏移距离的关系图。由图9 可知,M与k均随着L的增大而不断减小,互感减小趋势与耦合系数几乎一致。这种现象表明,对副边线圈长度为52mm 的旋转LCT 结构,随着轴向偏移距离的增大,其耦合程度在不断的降低。

图9 长度为52mm 时轴向偏移Fig.9 Axial offset at 52mm length
图10 为旋转LCT 副边长度为78mm 时,原、副边线圈互感、耦合系数与轴向偏移距离的关系图。此时原副边线圈长度相等,M与k均随轴向偏移距离L的增大呈现先增大后减小的趋势,互感下降的幅度最为明显,最小值为57.41μH。出现先增大现象的原因可能在于原边螺线管线圈两端存在稍大于其内部场强的磁场,使得LCT 的耦合程度提高。
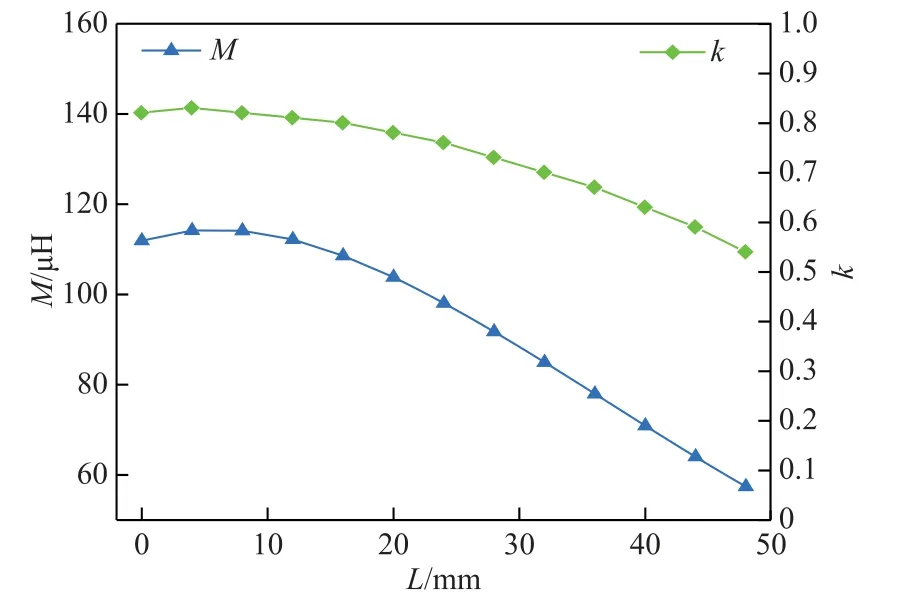
图10 长度为78mm 时轴向偏移Fig.10 Axial offset at 78mm length
图11 为旋转LCT 副边长度为78mm 时,副边线圈无偏移、偏移8mm 与偏移48mm 的磁场云图。

图11 磁场云图Fig.11 Magnetic field nephogram
由图11 可知,副边线圈偏移48mm 时,原、副边线圈之间的磁场较为发散,与之对应的图10 中此时互感值最小;副边线圈偏移8mm 时的磁场较原副边对齐情况略显集中,与之对应的图10 中副边线圈偏移8mm 的互感值略大于原、副边线圈完全对齐的情况。
图12 为旋转LCT 副边线圈长度为130mm 时,互感、耦合系数与轴向偏移距离的关系。随着轴向偏移距离L的增大,M在不断地减小。轴向偏移在0~12mm 范围内变化时,k几乎没有变化;在12~48mm 范围内变化时,k缓慢减小。

图12 长度为130mm 时轴向偏移Fig.12 Axial offset at 130mm length
由图9~图12 可知,互感值随副边线圈长度的增大而增大,随轴向偏移距离的增大而减小,与理论分析相一致。同时,副边线圈长度越长,其耦合系数k受轴向偏移影响越小。
3.2 轴向偏移对输出功率及效率的影响
由图13 可知,对于副边线圈长度为130mm、78mm、52mm 的三种情况,在0~48mm 范围内发生轴向偏移,DC-DC 效率受轴向偏移影响很小,其值较为接近,分别稳定在72%、75%、71%附近。
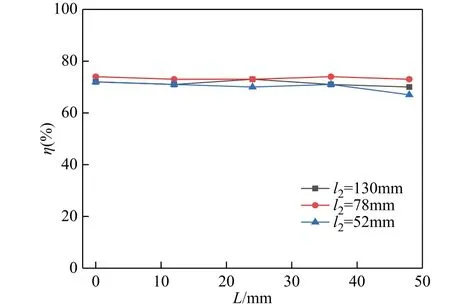
图13 DC-DC 效率随轴向偏移的变化Fig.13 Change of DC-DC efficiency vs. axial offset L
由图14 可知,线圈长度为130mm 的情况下,输出功率受轴向偏移影响较长度分别为78mm、52mm 的小,且长度为78mm 的情况下,输出功率随轴向偏移的增大而下降的趋势较长度为52mm 的情况稍缓,即副边线圈长度越长,旋转LCT 的输出功率抗轴向偏移能力越强。
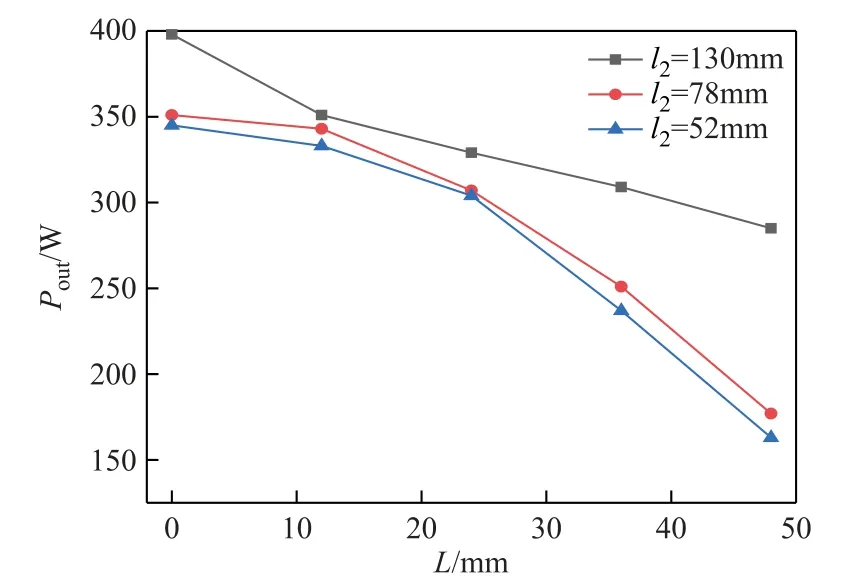
图14 输出功率变化Fig.14 Change of output power
4 仿真与实验验证
为了验证理论分析和结果的正确性,设计和开发了一套基于LCL_S 补偿结构的无线电能传输系统样机,如图15 所示。实验中采用JT6343A 直流电子负载,LW-10010KD 直流电源,系统所设计稳定运行的最大传输功率为1kW。实验参数见表1 与表2,系统谐振频率为50kHz,谐振参数依据式(3)选取,实验中选取副边长度为130mm 线圈结构进行实验验证。图16 为旋转LCT 实物,图中,副边线圈长度较原边线圈长,副边线圈匝数为37 匝。

图15 实验平台Fig.15 Experimental platform

图16 旋转LCT 实物Fig.16 Physical of rotary LCT
图17 为逆变输出电压、逆变输出电流及负载输出电压、负载输出电流的示波器波形。此时原、副边侧线圈偏移距离L为0,DC-DC 效率为72%。图中逆变输出电流滞后于逆变输出电压,主要在于计算补偿参数时理论计算值与实际匹配值有误差,以及副边后级电路反射到原边的等效电阻呈感性导致。
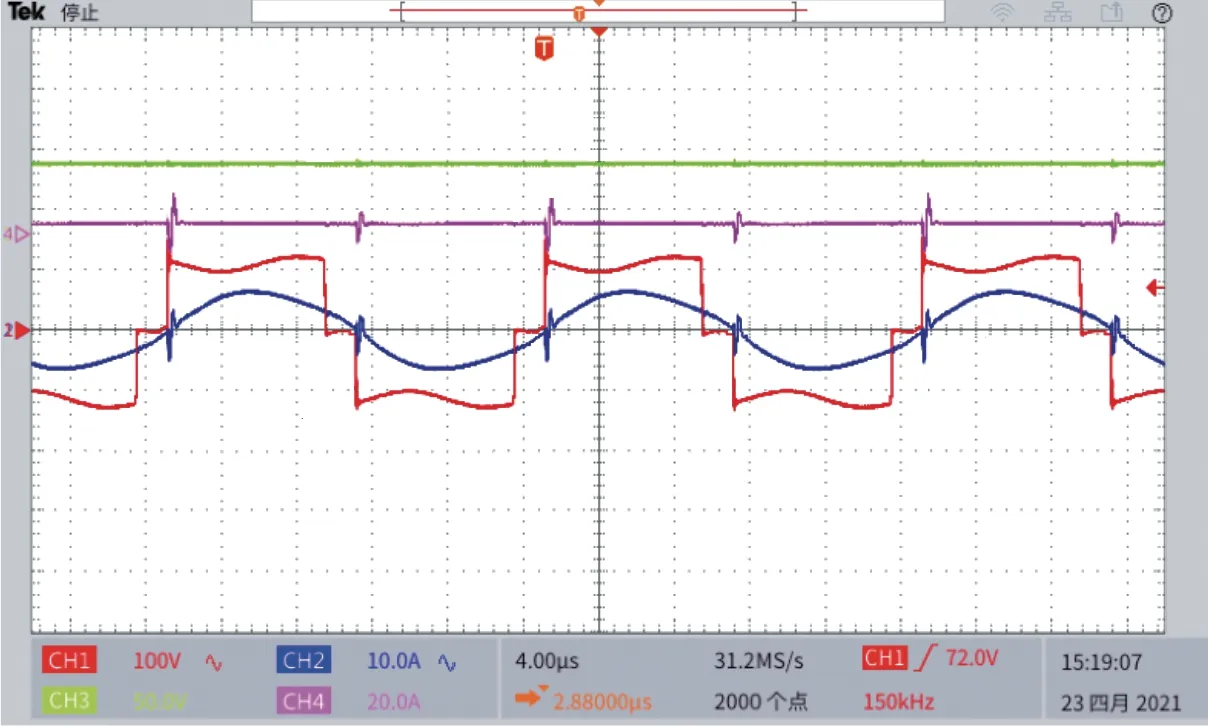
图17 输出电压、电流波形Fig.17 Waveforms of output voltage and output current
图18 为互感值的仿真计算实验对比,仿真结果与计算结果吻合的很好;在轴向偏移0~24mm 范围内,实验值较仿真计算值小约 9%;在轴向偏移24~48mm 范围内,实验值与仿真计算值偏差4%左右,均在允许的误差范围内。存在误差的主要原因在于线圈缠绕过程中,线圈之间存在空隙和缠绕不均匀的情况,而仿真与计算均假定线圈之间无空隙且均匀贴近磁心。

图18 互感仿真计算实验对比Fig.18 Comparison of mutual inductance under simulations, calculations and experiments
图19 为实验与仿真的DC-DC 效率值随轴向偏移距离变化曲线。图中仿真值稳定在72%左右,实验值稳定在68%左右,受轴向偏移的影响较小。实验值与仿真值产生偏差的主要原因在于实验过程中系统存在其他损耗,导致DC-DC 效率降低。

图19 DC-DC 效率仿真实验对比Fig.19 Comparison of DC-DC efficiency under simulations and experiments
图20 为输出功率随轴向偏移距离变化的实验值与仿真值的变化。由于实验过程中存在其他损耗,从而导致实验值较小。但从图20 可知,其变化趋势是一致的,均随轴向偏移距离的增大而不断减小;在轴向偏移48mm 时,较原来正对时的输出功率减小约30%,即系统的功率传输能力随轴向偏移的不断增加而不断减弱,且影响较大。
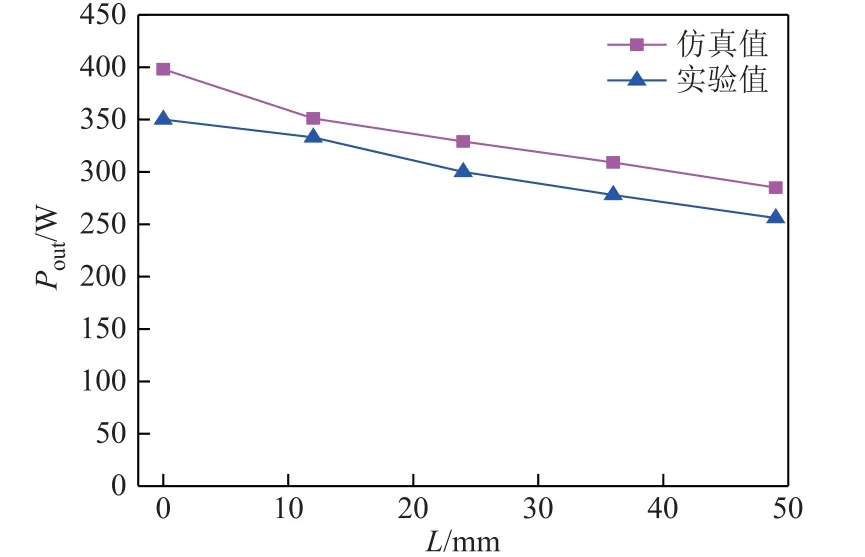
图20 输出功率仿真实验对比Fig.20 Comparison of output power under simulations and experiments
5 结论
本文以AUV 水下无线充电为研究背景,建立了旋转式LCT 互感计算模型,同时通过仿真分析了不同副边线圈长度条件下轴向偏移对旋转式 LCT耦合系数、输出功率及效率的影响,并搭建了实验平台进行实验验证,最后得到如下结论:
1)互感值与副边线圈长度呈正相关,同时轴向偏移越大耦合系数与互感值越小;副边线圈长度越长,耦合系数受轴向偏移影响越小。
2)轴向偏移越大,输出功率越小;且副边线圈长度越长旋转LCT 的抗轴向偏移能力越强,输出功率受轴向偏移影响越小。
3)旋转式LCT 的DC-DC 传输效率受轴向偏移的影响较小,即DC-DC 传输效率的抗轴向偏移能力较强。
