面向表面质量的工艺参数稳定域优化研究
2021-12-13陈娟娟巨孔亮
陈娟娟,巨孔亮
(1.西安工程大学服装与艺术设计学院,陕西 西安 710048)(2.西安工程大学机电工程学院,陕西 西安 710048)
铣削加工广泛应用于航空航天、船舶、电子等领域,其加工表面质量对工件品质至关重要。表面粗糙度和残余应力作为衡量表面质量的重要性能指标,也是铣削表面形貌评价和力学性能表征的主要评价指标[1-2]。为了使表面粗糙度和残余应力同时获得理想效果,提高铣削表面质量,对铣削过程的工艺参数控制成为关键。
工艺参数对表面粗糙度和残余应力的影响不同。对于表面粗糙度,毛玺等[3]进行了7075铝合金表面铣削试验,研究工艺参数与表面粗糙度之间的影响规律,获得了各加工因素最优参数水平;罗恒等[4]采用单因素法探究了铣削量对7A09铝合金铣削表面粗糙度的影响;Tlhabadira等[5]采用田口法研究了AISI P20铣削工艺参数对表面粗糙度的影响,建立表面粗糙度评价模型并获得最优解;Karkalos等[6]基于响应曲面法研究了工艺参数对Ti-6Al-4V ELI合金表面粗糙度的影响,建立模型并对铣削参数进行优化分析。对于残余应力,罗恒等[4]通过单因素法研究了铣削用量对7A09铝合金铣削表面残余应力的影响;郑耀辉等[7]采用有限元仿真与试验验证相结合的方法分析2024铝合金铣削表面残余应力随铣削参数的变化,并对铣削参数进行了优化;Wu等[8]针对Ti-10V-2Fe-3Al进行铣削正交试验,通过仿真分析和实验验证明确了切削参数对残余应力的影响及形成机理;Masmiati等[9]研究了S50C中碳钢铣削过程中润滑剂和铣削方式的影响,基于响应曲面法建立了残余应力的预测模型。上述研究均以工艺参数对表面质量单一指标的影响为中心,可能导致其他表面质量评价指标的失控。因此,本文在加工过程中兼顾多评价指标以对工件表面质量进行更全面的表征。
实际铣削加工过程中存在很多不可控因素,因此不仅要考虑到影响表面质量的多种因素,还需要找到可靠的工艺参数区间,以提高加工过程的稳定性。本文基于灰色关联分析将表面粗糙度和残余应力转化为灰色关联度(grey relational grade,GRG),针对GRG建立二阶回归响应模型,利用多参数全局相对灵敏度分析(multi-parameter global relative sensitivity analysis, MPGRSA)和单参数局部灵敏度分析(single parameter local sensitivity analysis,SPLSA)开展工艺参数对GRG影响研究,以获得工艺参数稳定域。
1 试验设计
选用φ1 mm的硬质合金铣刀在VMC850机床对7075铝合金工件进行干式切削。根据机床性能及经验,选取加工参数——主轴转速n、进给速度vf和轴向切深ap设计了三因素三水平BBD(box-behnken design)[10]试验。使用Mahr XT20表面粗糙度测量仪测量表面粗糙度,在PROTO LXRD MG2000测试中心分析残余应力,试验参数及测量结果见表1。
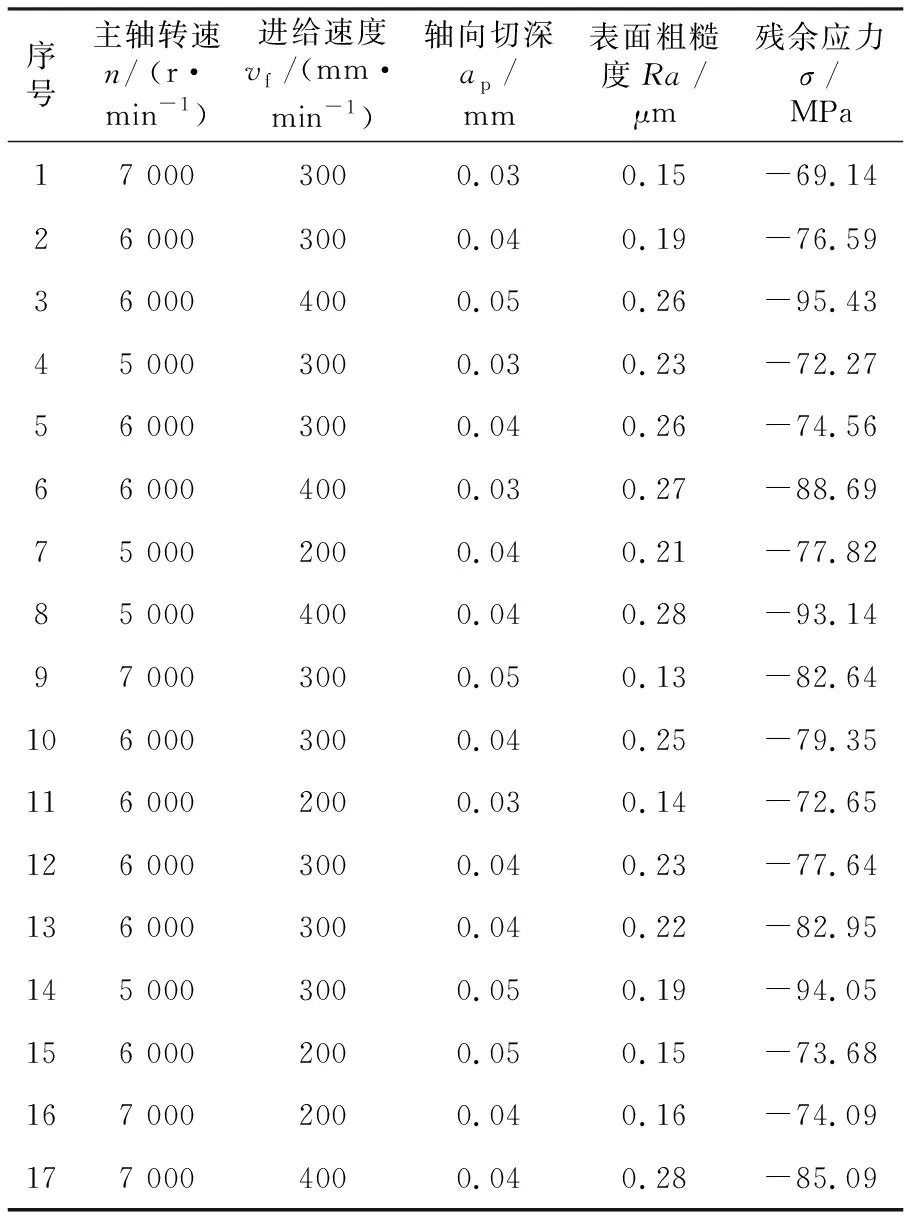
表1 试验参数安排及结果
2 多目标优化
由于表面粗糙度和残余应力量纲不同,难以同时达到最优,为了使两个指标同时达到较好效果,利用灰色关联分析法[11-12]将多目标转化为单目标进行表面质量分析。
灰色关联分析过程如下:
1)原始数据标准化处理:分别使用式(1)和式(2)对具有望大特性和望小特性的指标进行计算。
(1)
(2)
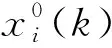

(3)
式中:Δ0i(k)为参考序列与第i个指标的比较序列第k组试验的绝对差值。
(4)
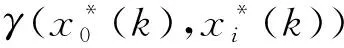
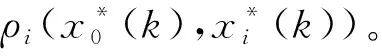
(5)
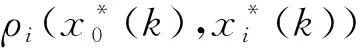
图1所示为表面粗糙度和残余应力优化为灰色关联度的结果。
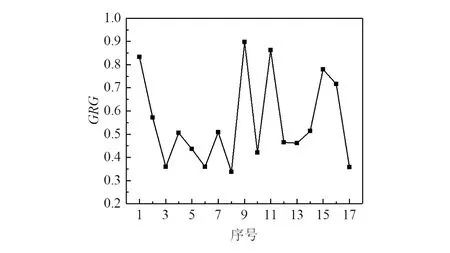
图1 多目标优化结果
3 结果与讨论
3.1 建立模型
本文以灰色关联度GRG为响应变量,利用Design-expert软件基于响应面法建立了工艺参数和响应变量之间的联系,得到响应变量的二阶回归模型:
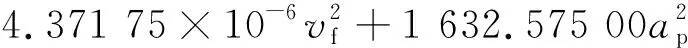
(6)
对模型进行了方差分析,结果表明,GRG模型的信度P=0.012 9<0.05,故模型显著。此外,绘出了模型的残差概率分布如图2所示,残差点均分布在直线附近,无明显异常残差,说明拟合效果较好,GRG模型可靠。
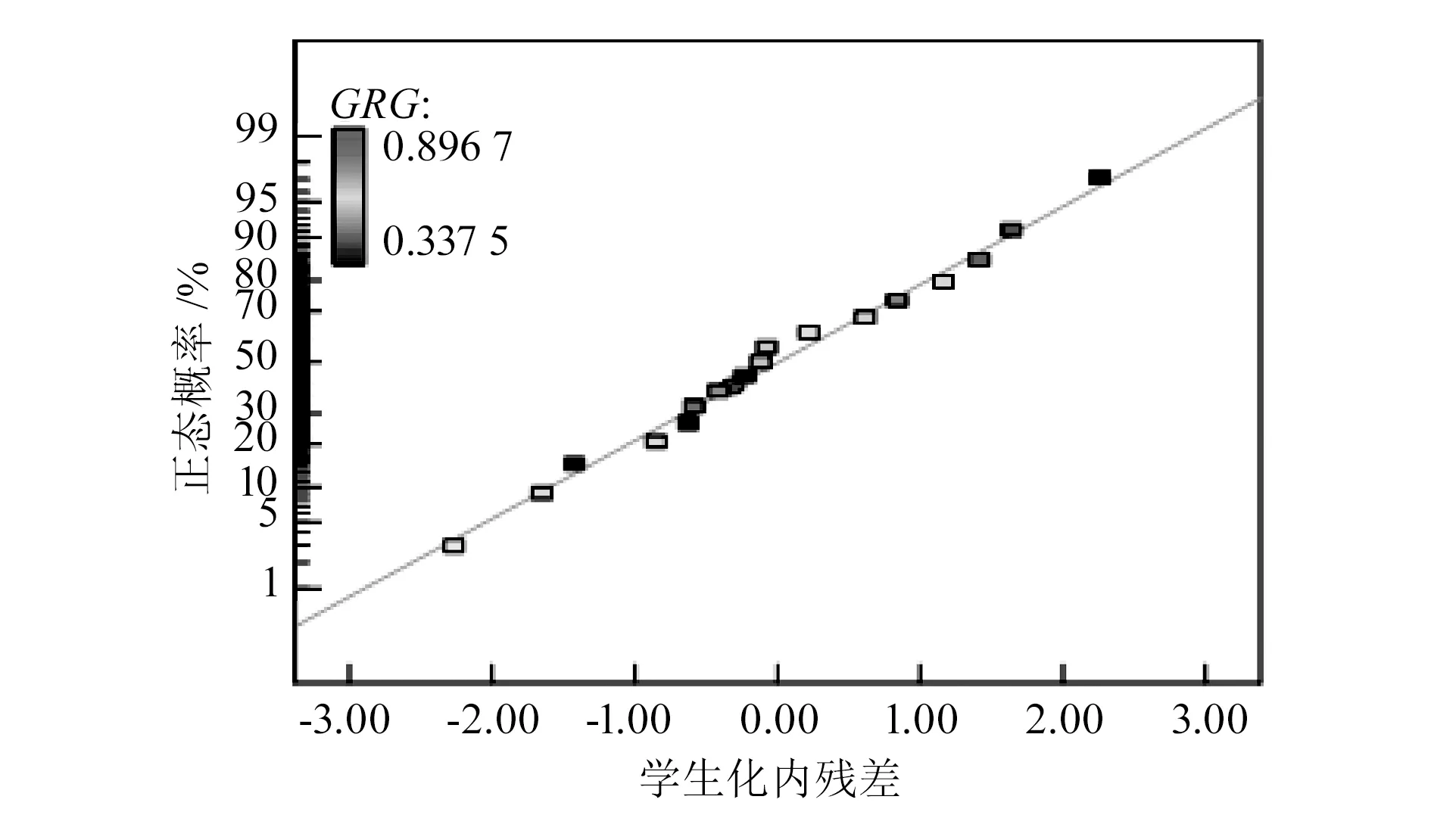
图2 模型的学生化内残差概率分布图
3.2 MPGRSA
MPGRSA从整体上揭示了工艺参数对响应的相对重要性[13-14]。具体过程为:将每个工艺参数随机生成均匀分布的序列,通过多次运行Monte Carlo模型获得相应目标值并计算平均值,经过比较确定可接受和不可接受的累积分布曲线,根据曲线之间的偏差度KS评估参数的相对灵敏度[15]。设定重复次数N为5 000,结果如图3所示。

图3 MPGRSA结果
KS越大表示灵敏度越大,由图3可知,在本文研究的参数范围内,进给速度为最敏感参数,主轴转速对GRG的影响次之,轴向切深对GRG影响最小。
3.3 SPLSA
SPLSA研究的是单工艺参数对响应的影响程度[13,16],反映响应f(x)对工艺参数xi的变化梯度,则灵敏度S(xi)可以表示为:
(7)
式中:Δxi为xi的增量。
分别计算铣削工艺参数的单参数局部灵敏度,其他固定参数设为n=6 000 r/min,vf=300 mm/min,ap=0.04 mm,单参数灵敏度模型如下:
(8)
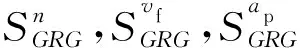
取工艺参数范围中值,将各工艺参数分为(Ⅰ)和(Ⅱ)两个区间,绘制单参数灵敏度曲线如图4所示。对于主轴转速和进给速度,参数在(Ⅱ)区间的灵敏度均值明显高于(Ⅰ)区间,灵敏度均值在两区间的变化幅度相同;轴向切深在两个区间的灵敏度均值无显著差异, (Ⅰ)区间和(Ⅱ)区间的灵敏度均值分别为16.484 5和16.170 1,即(Ⅰ)区间灵敏度变化范围略大于(Ⅱ)区间。
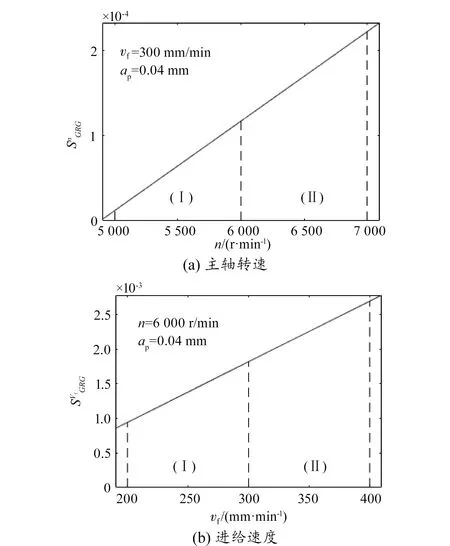
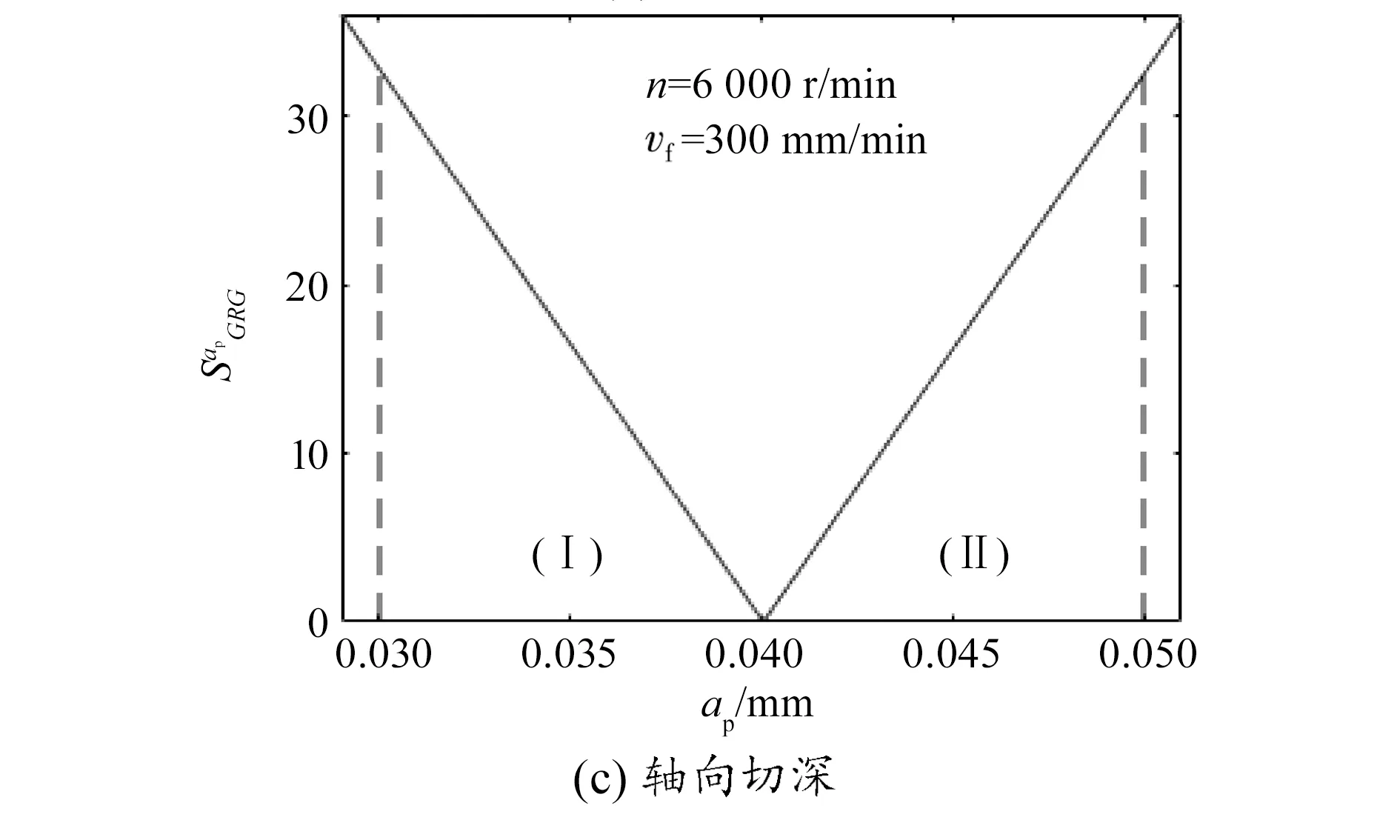
图4 SPLSA结果
3.4 稳定域优化分析
工艺参数的稳定域是指响应对工艺参数变化不敏感且响应较好的区间。由 MPGRSA结果可知,轴向切深的KS值相对于主轴转速和进给速度最小,对GRG的影响最小;SPLSA结果表明,主轴转速和进给速度两区间的灵敏度均值变化明显,而轴向切深的两区间灵敏度曲线几乎呈对称分布,灵敏度均值相差极小。因此,可以认为主轴转速和进给速度为GRG的敏感参数,需要进一步进行稳定域分析,而轴向切深为不敏感参数,其稳定域为整个区间。
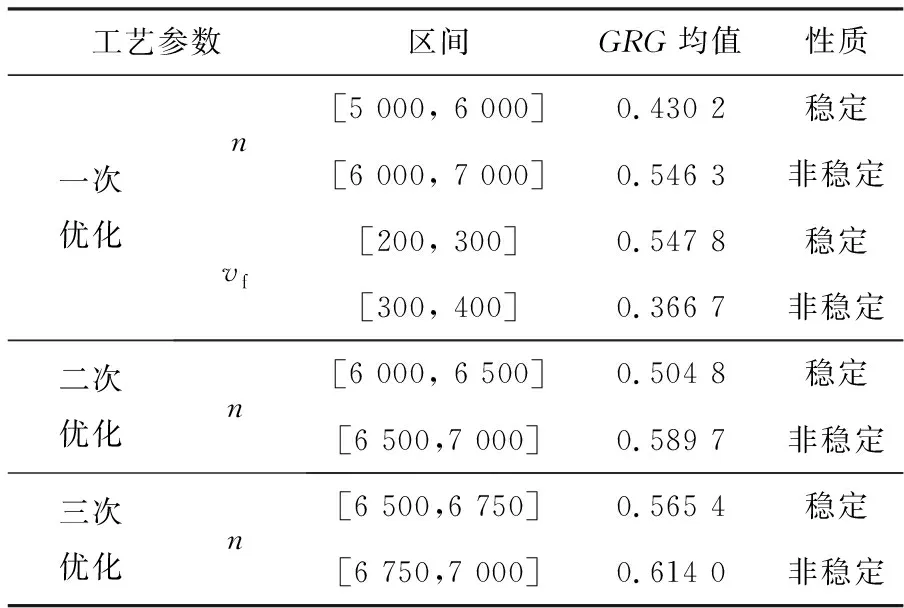
对于主轴转速和进给速度,分别计算工艺参数划分的两区间内SPLSA均值A1和A2,取A1和A2的均值记为A0,若Ai 表2 工艺参数的稳定区间和非稳定区间 为了进一步优化上述结果,分别在工艺参数的两区间随机选取5 000个点计算对应GRG均值。当稳定区间的GRG均值大于非稳定区间时,稳定区间优于非稳定区间,认为稳定区间为该工艺参数的稳定域,否则对非稳定区间取中值重新划分稳定区间和非稳定区间,继续进行上述分析,直到获得稳定域。参数稳定区间优化结果见表3。 分析表3可知,在一次优化过程中进给速度在(Ⅰ)区间的GRG均值优于(Ⅱ)区间,因此其稳定区间为稳定域;主轴转速在(Ⅰ)区间的GRG均值劣于(Ⅱ)区间,故对GRG均值更好的(Ⅱ)区间继续进行优化,经过二次优化和三次优化后主轴转速在(Ⅰ)区间的GRG均值仍然劣于(Ⅱ)区间,但是由于参数区间已经足够小,故不再需要进行优化,将GRG均值更优的区间作为稳定域。优化后铣削工艺参数稳定域分别为:主轴转速[6 750,7 000],进给速度[200,300],轴向切深[0.03,0.05]。 表3 优化的铣削工艺参数稳定区间 分别从稳定域和非稳定域中随机各选取3组工艺参数组合,对优化后工艺参数稳定域进行可靠性验证,前3组为稳定域,后3组为非稳定域,实验结果见表4所示。由表4可知,前3组稳定域参数实验得到的GRG均值优于后3组非稳定域的GRG均值,验证了稳定域优化的有效性。 表4 稳定域实验结果 表面粗糙度和残余应力都直接受到铣削工艺参数的影响,优化表面粗糙度和残余应力对提高铣削表面质量具有重要意义。为了同时获得较为理想的表面粗糙度和残余应力,利用灰色关联分析将多目标优化为GRG,建立基于响应曲面法的GRG的二阶回归模型。根据GRG模型分别对工艺参数进行了MPGRSA和SPLSA灵敏度分析,获得工艺参数的稳定域。MPGRSA结果表明,进给速度对表面质量的灵敏度最高,主轴转速次之,轴向切深最小,结合SPLSA结果可知轴向切深为不敏感参数,初步确定了工艺参数的稳定区间。对工艺参数稳定区间进行优化获得稳定域为:主轴转速[6 750,7 000],进给速度[200,300],轴向切深[0.03,0.05],验证了工艺参数稳定域的可靠性,为提高加工过程的稳定性和进一步控制铣削表面质量提供了依据。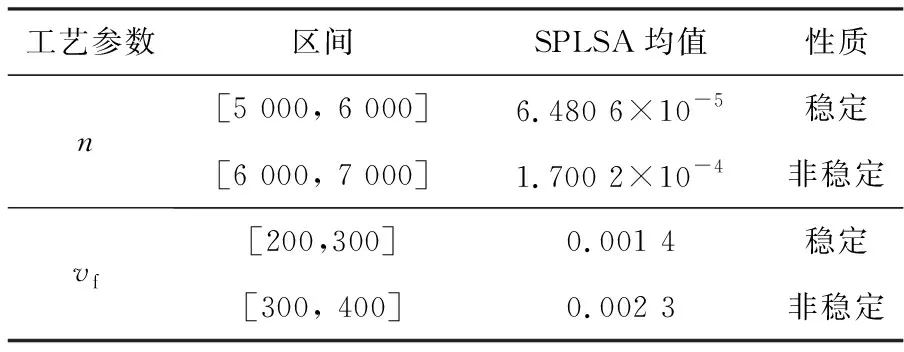
3.5 实验验证

4 结束语
