径锻压下率对镁棒热力参数及组织演变的影响
2021-12-13邹景锋马立峰朱艳春
邹景锋,马立峰,朱艳春
塑性成形
径锻压下率对镁棒热力参数及组织演变的影响
邹景锋,马立峰,朱艳春
(太原科技大学 机械工程学院,太原 030024)
通过径向锻造工艺制备大尺寸镁合金棒料,并研究ZK60镁合金稳定变形区轴向截面边部位置的组织演变规律。基于轴对称模型,利用数学解析方法建立不同压下率下的镁棒应变分量数学模型;使用弹塑性有限元分析软件对不同压下率下的镁棒径锻过程进行热力耦合分析;采用GFM-SSP32径锻机对铸态ZK60镁合金棒材进行阶梯锻造实验。随着径向压下量的增大,晶粒细化明显。当压下率达到62.29%时,孪生动态再结晶机制开动;与模拟结果相比,数学模型预测的平均相对误差约为8.4%,可较准确表征径锻镁棒的应变分布情况。径向锻造工艺完全可以制备ZK60镁合金棒材,并可有效解决镁合金塑性变形过程中的易开裂、散热快等问题。
镁合金;径向锻造;热力参数;组织演变
镁合金作为目前工程应用中最轻的金属结构材料,具有比强度高、比刚度高、阻尼减震性好、尺寸稳定性好、机加工方便、易于回收等优点,被誉为“21世纪绿色工程金属结构材料”[1],被广泛用于航空航天、国防军工、汽车、电子3C等高尖端领域[2—3]。镁及镁合金为密排六方晶体结构,具有散热快[4]、塑性变形温区窄等材料特性,导致镁合金低温塑性成形能力差,阻碍了镁合金的进一步开发和应用。常见的民用镁合金型材多以压铸件[5]和挤压件[6]为主,铸造及挤压组织特征显著。鉴于此,国内外的专家学者们做了大量研究,发现锻造技术诱导晶粒细化可显著提高镁合金的塑性。权高峰[7]等研究了镁合金轮毂的模锻工艺,制备了性能良好的镁合金轮毂。Miura[8—9]等对AZ31和AZ61合金进行低应变速率降温多向锻造,制备了平均晶粒尺寸分别为0.43 μm和0.8 μm的超细晶粒合金锭坯,发现其在高温低应变速率下具有超塑性。同时,Miura[10]等在室温低应变速率条件下,制备出屈服强度为530 MPa,抗拉强度为650 MPa的高强度AZ80镁合金锭坯。吴远志[11]发现AZ31合金多向锻造组织的演变可分为2个阶段,当累积应变小于1.32时,晶粒逐渐细化;当累积应变大于1.32时,再结晶晶粒在热激活作用下逐渐长大。目前,关于镁合金锻造的研究多集中在单向加载的多向锻造领域,以及壳体类零件的精密模锻,关于镁合金棒材径向锻造的研究尚未见报道。径向锻造工艺作为一种双向同步加载的高频锻打工艺(成形原理如图1所示),在提升锻件力学性能、表面成形质量、生产效率的同时,双向同步的多向加载方式可有效限制锻造过程中裂纹的萌生与扩展[12]。同时,高频锻打过程产生的变形热可对镁合金锻造过程中的温度散失予以补偿。径锻镁合金棒材在镁合金管材、轴类零件、医疗器械以及中低压压力容器等终端服役领域具有广阔的应用前景。此外,国内外学者对径向锻造的成形工艺做了大量研究,锻造的合金包括合金钢、钛合金、铍、铝、钨和超高温合金等[13—15],均获得了很好的成形效果。
文中以镁合金棒材为研究对象,以径向锻造为生产工艺,重点研究压下量的变化对镁合金棒径锻过程的影响。采用理论推导和有限元模拟相结合的方法,系统地研究不同压下率下,镁合金棒材径锻过程中的应变以及温度分布规律。通过GFM-SSP32径锻机进行ZK60棒材的阶梯锻造实验,研究不同压下率下,镁合金棒材组织的演变规律。

图1 径向锻造的成形原理
1 应变场理论模型推导、有限元模拟及实验方案制定
1.1 径锻过程的理论模型推导
工件的进给速度为,在相邻2次锻打期间,锤头和工件的相对轴向距离移动为,其中为锤头往复运动周期时长的一半。根据锤头的几何形状,可知锤头的每次径向压下量为:
=∙tan(1)
式中:为锤头入口角度。已知工件总的变形量为0−1,需要的锻造次数为=(0−1)/,0,1分别为棒材的始锻半径与终锻半径。
推导得出棒材的局部压下率为:
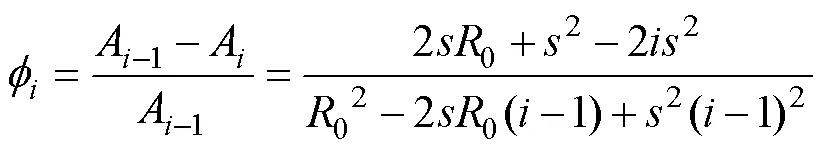
式中:为横截面面积;为打击次数,1≤≤。径向锻造过程中的锻造载荷呈对称分布,单锤变形量小,符合应力轴对称模型,由塑性力学知识得知,圆柱坐标系下应力平衡微分方程为[16]:

结合应力轴对称模型的特征,面上没有切应力,即τ=τ=0;各应力分量与坐标无关,故对的偏导数都为0。将式(3)进一步简化为:
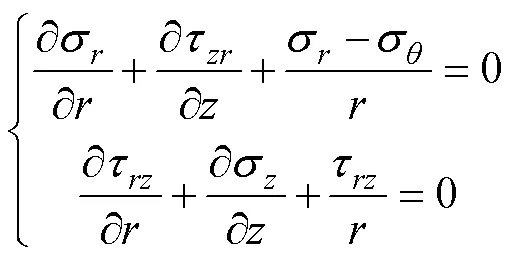
由塑性力学知识得知,圆柱坐标系下应变平衡微分方程为[16]:
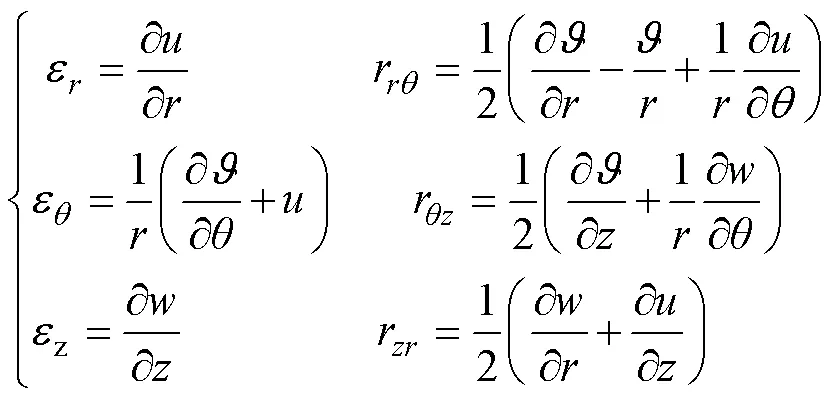
式中:,,分别为径向、周向、轴向位移分量。当轴对称塑性变形时,子午面始终保持平面,周向位移分量v=0,故r=r=0,径锻工艺的应变分量为:

由体积不变原理得:
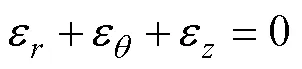
假设工件在径向锻造过程中,各横截面材料轴向流动均匀,即z为与无关的常量。求解微分方程得:
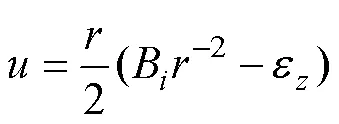
进而得到锻造过程中第个截面变形产生的轴向应变增量式:



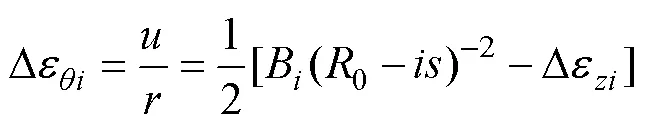
1.2 热力耦合有限元模型的建立
采用FEM分析软件Abaqus-Explicit建立镁合金棒材径锻工艺的热力耦合模型,其中所用棒料规格为142 mm,锤头入口角度为8°,打击频次为每分钟300次。模型采用温度-位移耦合的显示动力学分析方法,充分考虑传热学的影响,设立了锤头与工件间的摩擦生热(剪切摩擦因数为0.6[17])、镁棒自身的热传导系数(117 W/(m∙k)[18])以及工件与空气间的对流散热系数(综合对流换热系数为19 W/(m2·K)[19])。模型通过设置多分析步模拟工件的多道次热锻过程,各道次累积压下率分别为17.40%,41.15%和62.29%。结合现场实验工况,工件采用步进式螺旋送进方式,送进速度为750 mm/min,并认为锤头的运动符合正弦曲线=12sin(31.4)。具体有限元模型如图2所示,设定累计分析步时间为52 s。

图2 镁合金棒材径锻工艺有限元模型
1.3 实验方案
所用材料为142 mm的铸态ZK60镁合金棒材,化学成分如表1所示。采用随炉加热方式,升温速度为10 ℃/min,当温度达到350 ℃时,保温3 h,随后利用GFM-SSP32径锻机,开展ZK60镁合金棒材的阶梯锻造实验,棒料阶梯锻造的各道次单边总压下量分别为6.5 mm(17.40%),10 mm(41.15%),11.25 mm(62.29%),经过锤头多次打击(锻造)加工成形。为避免多次加热诱导的热激活效应对实验结果产生干扰[20],中间不进行二次加热(补热),锻后空冷,如图3所示[21]。由图3b不难发现,锻后工件表面质量良好,未出现裂纹。随后,对同一根棒材未变形区以及3个压下量下的外圈横截面组织,进行微观组织形貌观察。
表1 ZK60镁合金的化学成分(质量分数)

Tab.1 Chemical composition of ZK60 magnesium alloy (mass fraction) %

图3 ZK60镁合金的阶梯锻造实验
2 结果与分析
2.1 应变场理论计算结果
通过应变场理论式(9—11)分别计算不同压下率下的棒材外圈的径向应变分量(11)、切向应变分量(22)和轴向应变增量(33),对计算结果进行拟合,结果如图4所示。11,22,33曲线的校正决定系数(Adjust.R-Square)分别为0.992 22,0.999 89,0.999 55。
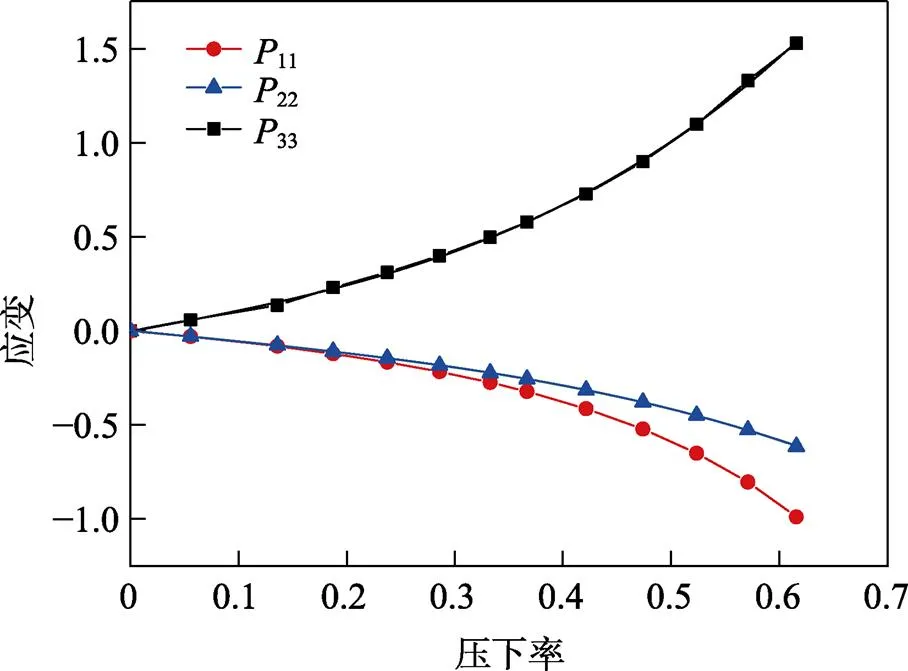
图4 应变场理论计算及拟合结果
2.2 模拟结果
为了与应变场理论计算结果进行相互验证,对不同压下量的ZK60镁合金棒材的应变分量进行了有限元模拟,如图5所示[21]。在径向锻造过程中,当等效应变值达到0.2时,坯料被锻透[22]。在第1道次时(如图5a所示,压下率为17.40%),心部应变值已高于0.2。低应变区(应变值≤1/3max的区域,其中max为该截面的应变最大值)的面积占棒材横截面面积的比值较高;相对均匀应变区(应变值为1/3max~2/3max的区域)占棒材横截面面积的比值(面占比)相对较小。如图5b所示,随着道次的增加,棒材整体应变呈上升趋势,径向方向上,低应变区的横截面面积占比降低,相对均匀应变区域的横截面面积占比显著上升。如图5c所示,当压下率达到62.29%时,棒材心部的应变值已大于0.8,棒材整体应变值以及相对均匀变形区的面积占比进一步提高。由此可见,随着压下量的增加,相对均匀变形区的面积占比逐步提高,有利于提高镁合金棒材径向方向上的组织均匀性。周向上应变差值极小,可忽略周向应变对组织演变的影响。

图5 不同压下率的ZK60镁合金棒材等效应变分布
提取了锻后棒材不同变形量下的应变分量模拟结果,与理论计算结果进行对比,如图6所示。经统计,应变场理论结果的平均相对误差仅为8.4%,可见,通过应变场理论计算模型能够较好地预测镁合金棒材径向锻造过程中的应变变化规律。

图6 应变场理论计算及模拟结果对比
此外,通过模拟不同压下量的ZK60镁合金棒材径锻过程,观察到一个有趣的现象,锻后棒材的温度不降反升,如图7所示。当应变速率为7 s−1时,随着压下率的增加,棒材整体呈升温趋势,且温升幅度沿径向由内向外逐渐增大,其中最后一道次外圈总温升高至34.8 ℃。在ZK60的阶梯锻造实验中,也观察到了这一现象。
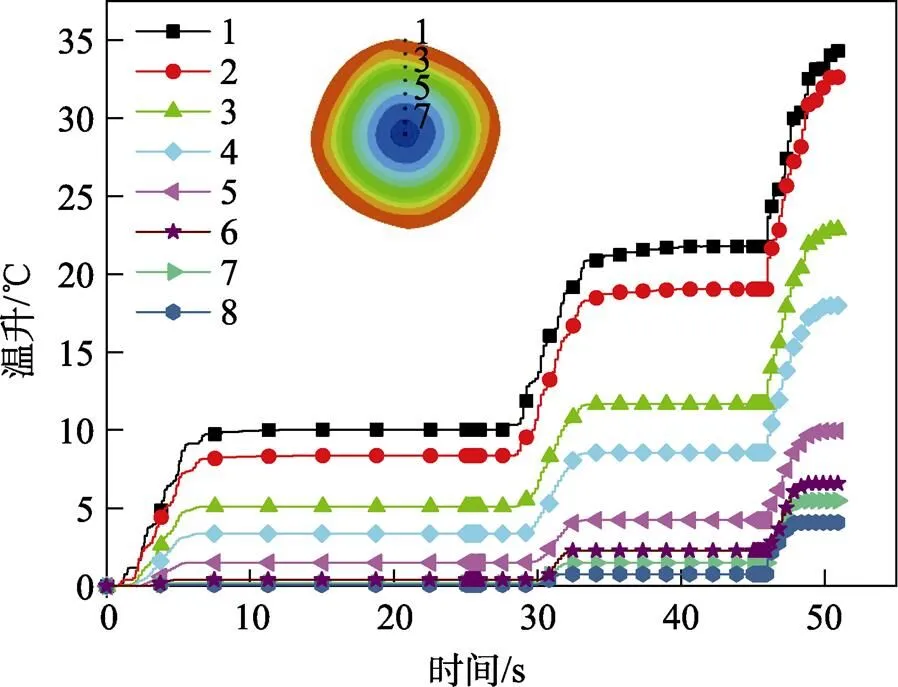
图7 ZK60镁合金棒材各取样点的时间历程温升曲线
棒材变形过程中的热量主要来源于径锻过程中机械能转化为金属塑性变形时产生的变形热,以及金属与模具之间摩擦做的功。传统塑性变形工艺的应变速率较低,在变形过程中,单位时间内由机械能转化的变形热有限,不足以补偿棒材在空气中的散热以及与模具间的热量流失,致使棒材整体温降严重。在径向锻造过程中,由于单位时间内对棒材的打击频次增加,应变速率明显提高,螺旋送进的进给方式以及4个锤头的高频同步脉冲锻打使棒材周向和轴向均匀分布了多个热源,极好地弥补了锻造过程中的热量损失,提高了棒材变形过程中温度分布的均匀性。此外,锤头与棒材外表面间的摩擦生热,也是造成锻后温升的原因之一。
2.3 不同压下率下的ZK60镁合金微观组织形貌及分析
为了进一步验证理论计算和数值模拟的应变场变化规律,分析在径向锻造过程中,ZK60镁合金应变对组织演变的影响,开展了阶梯实验,并对不同压下量的显微组织进行了观察,如图8所示。图8a为锻造前ZK60镁合金的原始显微组织,图8b—d是应变速率为7 s−1,压下率分别为17.40%,41.15%,62.29%时,径向锻造稳定变形区横截面边部位置的金相组织。由图8可知,随着压下率的增加,单位面积内的晶粒数量逐步增多,再结晶晶粒数量增多,晶粒尺寸逐渐细化。此外,由图8a可知,初始材料的晶粒比较粗大,呈等轴分布,晶粒尺寸约为20~30 μm。由图8b可知,经较小压下率的径向锻造后,晶粒细化不明显,部分晶界的位置发生了晶粒变形破碎,少数晶界周围发现了动态再结晶晶粒。随着累积压下率增加至41.15%,如图8c所示,大部分原始晶粒被破碎,孪生机制开动,晶粒尺寸细化,动态再结晶晶粒数量增多;当压下率达到62.29%时(见图8d),晶粒细化更显著,界面内布满了细小的动态再结晶晶粒,局部区域晶粒尺寸达到纳米级,同时,孪晶数量增多,值得注意的是,在部分孪晶内观察到了动态再结晶现象。

图8 ZK60镁合金在不同压下率下的光学显微组织
滑移、孪生和晶界滑移(GBS)是镁合金塑性变形的主要机制。晶界滑移是镁合金中最重要的晶间变形机制,由于GBS通常只有在高温低应变速率下才能发生,且在实验过程中,加热炉离径锻机距离较远,期间散热较多,同时,所用材料的初始组织较为粗大,故镁合金在高应变速率径向锻造过程中,GBS难以发挥明显作用。此外,当径向锻造过程中的应变速率较大时,不利于相邻晶粒间滑移的传播和连续性,因此,当变形量累积到一定程度时,会引起晶界附近较大的应力集中,此时单纯的滑移难以释放应力,必须依靠孪生或裂纹的萌生和扩展来协调形变和释放应力[23]。
结合应变分布云图(图5c)进一步分析得知,当压下率达到62.29%时,镁合金棒材的边部应变值剧增,位错塞积严重,单纯的滑移已不足以释放集中应力。研究表明,裂纹的萌生和扩展均可释放应力,且裂纹多由拉应力引起,沿大致垂直于最大拉应力的方向传播[24—25]。径向锻造同步双向对称的加载方式在一定程度上遏制了裂纹的萌生和扩展[12]。为释放径向锻造过程中的应力集中,需引入裂纹的竞争机制——孪生。孪生作为协调形变和释放应力的有效方式,其形核速度大于裂纹的萌生和扩展速度[26],在释放径锻过程中的应力集中时,可发挥重要作用。综上,如图8d所示,当压下率累积达62.29%时,孪晶数量明显增多。
此外,孪晶界阻碍位错运动作为再结晶的储能方式,以及孪晶界和晶界附近亚结构取向差的存在,极易诱导动态再结晶在孪晶内形核[27]。如图8d所示,当压下率达到62.29%时,部分区域的孪晶已极为密集。在径向锻造变形过程中,孪晶界阻碍了位错运动,导致孪晶界附近位错塞积严重,为了释放孪晶界阻碍位错运动产生的集中应力,孪晶界周围的塞积位错重排,孪生再结晶机制开动。
3 结语
基于轴对称模型,利用数学解析方法确定了铸态ZK60镁合金棒材径锻过程中的应变场数学模型,模型预测的平均相对误差约为8.4%。
镁合金经高频锻造产生的变形热极好地弥补了镁合金材料散热快、塑性变形温区窄的塑性变形劣势,锻后温升高达34.8 ℃。通过后续对工艺参数的优化,在不采取加热以及保温(补温)的前提下,可实现“近等温”锻造。对提高镁合金棒材组织的均匀性,以及锻造过程中组织演变的控制极为有利。
ZK60镁合金在径向锻造过程中的组织演变分为3个阶段,当压下率≤17.4%,其晶粒细化机制多为机械式击碎,晶界处有少量再结晶晶粒;当17.4%˂压下率≤41.15%时,晶粒细化机制主要为形变诱导动态再结晶,孪晶较少;当41.15%˂压下率≤62.29%时,晶粒尺寸细化明显,孪晶增多,受孪晶晶界阻碍,孪生再结晶机制开启。
[1] 查敏, 王思清, 方圆, 等. 高性能轧制镁合金研究进展[J]. 精密成形工程, 2020, 12(5): 20—27.
ZHA Min, WANG Si-qing, FANG Yuan, et al. Research Progress of High Performance Rolling Magnesium Alloys[J]. Journal of Netshape Forming Engineering, 2020, 12(5): 20—27.
[2] 潘虎成, 武华健, 程仁山, 等. Al、Mn元素对Mg-2.5Sn-3.5Ca合金微观组织与力学性能的影响[J]. 精密成形工程, 2020, 12(5): 28—36.
PAN Hu-cheng, WU Hua-jian, CHENG Ren-shan, et al. Effect of Al and Mn on Microstructure and Mechanical Properties of Mg-2.5Sn-3.5Ca Alloy[J]. Journal of Netshape Forming Engineering, 2020, 12(5): 28—36.
[3] 郑兴伟, 赵宗, 汪伟, 等. Mg-Nd-Zn-Zr稀土镁合金无缝管材正反挤压过程模拟[J]. 精密成形工程, 2020, 12(5): 59—65.
ZHENG Xing-wei, ZHAO Zong, WANG Wei, et al. Simulation of Forward and Back Extrusion Process of Mg-Nd-Zn-Zr Seamless Tube[J]. Journal of Netshape Forming Engineering, 2020, 12(5): 59—65.
[4] 汪凌云, 黄光杰, 陈林, 等. 镁合金材轧制工艺及组织性能分析[J]. 稀有金属材料与工程, 2007, 36(5): 910—914.
WANG Ling-yun, HUANG Guang-jie, CHEN Lin, et al. Research on Rolling Technology of Magnesium Alloy Sheets[J]., 2007, 36(5): 910—914.
[5] 李荣德, 于海朋, 袁晓光. 压铸技术及压铸合金的发展与应用[J]. 机械工程学报, 2003, 39(11): 68—73.
LI Rong-de, YU Hai-peng, YUAN Xiao-guang. Development and Application of the Die-Casting Technology and Alloy[J]. Chinese Journal of Mechanical Engineering, 2003, 39(11): 68—73.
[6] 李落星, 周佳, 张辉. 车身用铝、镁合金先进挤压成形技术及应用[J]. 机械工程学报, 2012, 48(18): 35—43.
LI Luo-xing, ZHOU Jia, ZHANG Hui. Advanced Extrusion Technology and Application of Aluminium, Magnesium Alloy for Vechicle Body[J]. Chinese Journal of Mechanical Engineering, 2012, 48(18): 35—43.
[7] 高建良, 章桢彦, 靳丽, 等. 镁合金锻造研究综述[J]. 热加工工艺, 2012, 41(15): 104—108.
GAO Jian-liang, ZHANG Zhen-yan, JIN Li, et al. Review on Forging Forming Technology of Magnesium Alloy[J]. Hot Working Technology, 2012, 41(15): 104—108.
[8] MIURAL H, YU G, YANG X. Multi-Directional Forging of AZ61 Mg Alloy under Decreasing Temperature Conditions and Improvement of Its Mechanical Properties[J]. Materials Science & Engineering A, 2011, 528(22): 6981—6992.
[9] MIURA H, YANG X, SAKAI T. Evolution of Ultra Fine Grains in AZ31 and AZ61 Mg Alloys during Multi Directional Forging and Their Properties[J]. Materials Transactions, 2008, 49(5): 1015—1020.
[10] MIURA H, NAKAMURA W, KOBAYASH M. Room-Temperature Multi-Directional Forging of AZ80 Mg Alloy to Induce Ultrafine Grained Structure and Specific Mechanical Properties[J]. Procedia Engineering, 2014, 81: 534—539.
[11] 吴远志, 严红革, 朱素琴, 等. 多向锻造ZK60镁合金组织和性能的均匀性[J]. 中国有色金属学报, 2014, 24(2): 310—316.
WU Yuan-zhi, YAN Hong-ge, ZHU Su-qin, et al. Homogeneity of Microstructure and Mechanical Properties of ZK60 Magnesium Alloys Fabricated by High Strain Rate Triaxial-Forging[J]. Transactions of Nonferrous Metals Society of China, 2014, 24(2): 310—316.
[12] 王连东, 高全德, 梁晨, 等. 径向精密锻造机V字锥形锤砧锻造分析及数值模拟[J]. 机械工程学报, 2011, 47(20): 146—151.
WANG Lian-dong, GAO Quan-de, LIANG Chen, et al. Deformation Analysis and Numerical Simulation of V-Shaped Cone Anvil Forging in the Fine Forging Machine[J]. Chinese Journal of Mechanical Engineering, 2011, 47(20): 146—151.
[13] 王永飞, 赵升吨, 范淑琴, 等. 径向锻复合单向压缩变形-再结晶熔融法制备半固态坯料的研究[J]. 稀有金属材料与工程, 2017, 46(10): 2900—2907.
WANG Yong-fei, ZHAO Sheng-dun, FAN Shu-qin, et al. Semi-Solid Billet Prepared by Radial Forging Combined with Unidirectional Compression Recrystallization and Partial Melting[J]. Rare Metal Materials and Engineering, 2017, 46(10): 2900—2907.
[14] FAN L, WANG Z, WANG H. 3D Finite Element Modeling and Analysis of Radial Forging Processes[J]. Journal of Manufacturing Processes, 2014, 16(2): 329—334.
[15] 卞祝, 葛清蕴. HRB500高强钢筋钢纤维混凝土梁受剪试验和承载力计算[J]. 重庆工商大学学报(自然科学版), 2018, 35(2): 94—99.
BIAN Zhu, GE Qing-yun. Experimental Study on Shear Resistance of Steel Fiber HRB500High-Strength Reinforced Concrete Beams and Calculation of Shear Capacity[J]. Journal of Chongqing Technology and Business(Natural Sciences Edition), 2018, 35(2): 94—99.
[16] 俞汉清. 金属塑性成形原理[M]. 上海: 机械工业出版社, 1999: 79—85.
YU Han-qing. Metal Plasticity Forming Theory[M]. Shanghai: China Machine Press, 1999: 79—85.
[17] CHEN J, CHANDRASHEKHARA K, MAHIMKAR C, et al. Study of Void Closure in Hot Radial Forging Process Using 3D Nonlinear Finite Element Analysis[J]. International Journal of Advanced Manufacturing Technology, 2012, 62(9/10/11/12): 1001—1011.
[18] 王春明, 陈云贵, 肖素芬, 等. 铸造Mg-3Zn- (0.5~3.5)Sn合金的导热率和机械性能[J]. 稀有金属材料与工程, 2013, 42(10): 2019—2022.
WANG Chun-ming, CHEN Yun-gui, XIAO Su-fen, et al. Thermal Conductivity and Mechanical Properties of as-Cast Mg-3Zn-(0.5~3.5)Sn Alloys[J]. Rare Metal Materials and Engineering, 2013, 42(10): 2019—2022.
[19] DING Y P, ZHU Q, LE Q C, et al. Analysis of Temperature Distribution in the Hot Plate Rolling of Mg Alloy by Experiment and Finite Element Method[J]. Journal of Materials Processing Technology, 2015, 225: 286—294.
[20] 简炜炜, 康志新, 李元元. 多向锻造ME20M镁合金的组织演化与力学性能[J]. 中国有色金属学报, 2008, 18(6): 1005—1011.
JIAN Wei-wei, KANG Zhi-xin, LI Yuan-yuan. Microstructural Evolution and Mechanical Property of ME20M Magnesium Alloy Processed by Multidirectional Forging[J]. Transactions of Nonferrous Metals Society of China, 2008, 18(6): 1005—1011.
[21] ZOU J F, MA L F, JIA W T, et al. Microstructural and Mechanical Response of ZK60 Magnesium Alloy Subjected to Radial Forging[J]. Journal of Materials Science & Technology, 2021, 83: 228—238.
[22] 董节功, 周旭东, 朱锦洪, 等. 径向锻造三维成形锻透性的数值模拟[J]. 机械工程材料, 2007, 31(3): 76—78.
DONG Jie-gong, ZHOU Xu-dong, ZHU Jin-hong, et al. FEM Simulation of Forging Penetration Efficiency of Radial Forging in 3D[J]. Materials for Mechanical Engineering, 2007, 31(3): 76—78.
[23] 熊爱明. 钛合金锻造过程变形-传热-微观组织演化的耦合模拟[D]. 西安: 西北工业大学, 2003: 110—116.
XIONG Ai-ming. Coupled Simulation of Deformation-Hsat Transfer-Microstructural Evolution for Forging Processes of Titanium Alloys[D]. Xi'an: Northwestern Polytechnical University, 2003: 110—116.
[24] ZHU S Q, YAN H G, CHEN J H, et al. Effect of Twinning and Dynamic Recrystallization on the High Strain Rate Rolling Process[J]. Scripta Materialia, 2010, 63(10): 985—988.
[25] ZHENG M Y, ZHANG W C, WU K, et al. The Deformation and Fracture Behavior of SiCw/AZ91 Magnesium Matrix Composite during in-Situ, TEM Straining[J]. Journal of Materials Science, 2003, 38(12): 2647—2654.
[26] ZHU S Q, YAN H G, LIAO X Z, et al. Mechanisms for Enhanced Plasticity in Magnesium Alloys[J]. Acta Materialia, 2015, 82: 344—355.
[27] 詹美燕, 李春明, 尚俊玲. 镁合金的塑性变形机制和孪生变形研究[J]. 材料导报, 2011, 25(3): 1—7.
ZHAN Mei-yan, LI Chun-ming, SHANG Jun-ling. Investigation of the Plastic Deformation Mechanism and Twinning of Magnesium Alloys[J]. Materials Review, 2011, 25(3): 1—7.
Effect of Radial Forging Reduction Rate on Thermodynamic Parameters and Microstructure Evolution of Magnesium Alloy Bar
ZOU Jing-feng, MA Li-feng, ZHU Yan-chun
(School of Mechanical Engineering, Taiyuan University of Science and Technology, Taiyuan 030024, China)
This paper aims to prepare the large-size magnesium alloy bar through radial forging process and study the microstructure evolution of the axial section edge in the stable deformation zone of ZK60 magnesium alloy. Based on the axisymmetric model, a mathematical model of the strain components of magnesium rods with different reduction rates was established by the mathematical analysis method; the thermal coupling analysis was carried out for the radial forging process of magnesium bars with different reduction rates by the elastic-plastic finite element analysis software; the step forging experiment was carried out on the cast ZK60 magnesium alloy bars by the GFM-SSP32 radial forging machine. The results showed that the grain refinement is obvious with the increase of radial reduction, and the twinning dynamic recrystallization mechanism is turned on when the depression rate reaches 62.29%; compared with the simulation results, the average relative error predicted by mathematical model is about 8.4%, which can more accurately characterize the strain distribution of the radial forging magnesium bars. The radial forging process can completely prepare ZK60 magnesium alloy bars, and effectively solve the problems of easy cracking and fast heat dissipation during the plastic deformation of magnesium alloy.
magnesium alloy; radial forging; thermodynamic parameters; microstructure evolution
10.3969/j.issn.1674-6457.2021.06.011
TG314.3
A
1674-6457(2021)06-0084-07
2020-04-26
国家自然科学基金(U1910213,51501122);山西省重点研发计划(201903D121088)
邹景锋(1993—),男,博士生,主要研究方向为轻质金属变形机理及组织性能。
马立峰(1977—),男,教授,主要研究方向为大型冶金装备设计理论与成套技术、镁合金变形理论与装备技术、金属材料轧制复合理论与装备技术。
