基于CFD技术的舵叶翼型选用分析
2021-12-12耿国祥董有凡何金帅
耿国祥,胡 义,董有凡,王 帆,何金帅
(武汉理工大学 能源与动力工程学院,湖北 武汉 430063)
0 引 言
舵是决定操纵性和快速性优劣的主要设备之一,但是目前其设计选型还是沿用传统的方法,即根据已有的母型船资料和经验确定舵的类型和数目,然后依据经验公式和相关规范要求评估水动力性能。
传统方法依据规范中的经验公式确定的相关参数虽然计算简单,但是得出的结果往往过于保守。而且未对不同舵叶翼型剖面的水动力性能进行模拟仿真,只是依赖母型船数据确定舵叶翼型,导致选型全面性不足。
近年来随着计算机性能与计算流体力学的快速发展,通过CFD软件对舵叶的水动力性能仿真逐渐成为研究热点。国内外很多学者用CFD对舵叶翼型开展过不少研究,李胜忠[1]构建了翼型水动力优化平台,为翼型选型设计提供思路;马玉成等[2]用CFX对敞水舵的水动力性能进行了分析,证明数值仿真和实验数据吻合性较好;周广礼等[3]对敞水舵水动力计算提出4种简化方法,为水动力计算提供理论支持。杨建民[4]和喻红霞[5]基于面元法对鱼尾舵的水动力计算提出新方法,结果表明可显著提高船舶操纵性。周轶美等[6]研究了高效翼型在潜艇上的应用,仿真结果与拖曳水池实验对比表明可显著提高潜艇操纵效率。朱文蔚等[7]提出的WZF系列鱼尾舵比传统的NACA系列升力系数提高了1.5倍,有广泛的应用前景。
本文通过CFD软件,基于SSTk-ω湍流模型和有限体积法对NACA翼型和优化后的高效翼型在均匀流场中进行数值模拟,在不同攻角下通过粘性流场得到其阻力系数和升力系数,结合速度矢量图和压力云图评估水动力性能,并以Exploration号极地邮轮为实例,与公式法和舵模换算数据进行对比分析,最终验证仿真结果可以为实船选型提供参考依据。
1 数学模型
1.1 控制方程
本文将求解不可压缩流体的RANS方程作为求解舵叶在三维粘性流场中的基本方程[7]。
1.2 湍流模型
SSTk-ω模型是由Menter提出并推广的,该模型的特点是对近壁面和边界层的流动采用不同的处理方式。李锦林[8]对敞水舵分别采用SSTk-ω模型和RNGk-ω模型进行水动力仿真,并与泰勒水池实验进行对比,结果证明SSTk-ω模型在水动力数值仿真结果方面相比与RNGk-ω模型有更高的精度。本文的湍流模型也采用SSTk-ω模型,用CFD模拟计算的过程中,假设水为不可压缩流体且在操舵时船舶方向与航速未发生变化,并忽略水流流过舵叶时的热量交换。
1.3 数值方法
离散化方法采用有限体积法,压力方程采用标准的离散格式进行离散,对动量方程[9]、耗散方程以及湍流动能方程采用2阶迎风格式进行离散,压力与速度耦合算法采用SIMPLE算法,采用非结构网格对整个流域进行网格划分,对流场与舵叶的接触面附近网格进行加密处理。
2 水动力计算理论
2.1 舵叶在流场中的受力
舵叶在水流中的受力与有限翼展的飞机机翼在空气中的受力相似。在均匀流场中舵叶表面水流流速不同使得压力变化产生压差,压差变化导致的升力变化就会影响船舶的操纵性。水流掠过翼型表面时会产生阻力,影响船舶的快速性。
对舵叶在均匀流场中进行受力分析后,相关符号及无因次量如下:

式中:Pn为法向力,N,Pl为升力,N;Pd为阻力,N;AR为舵叶在中纵剖面上的投影面积, m2; ρ为水的密度, k g/m3,V为水流速度, m /s。
2.2 传统水动力计算方法
1)经验公式法
乔塞尔公式[10]是计算水动力性能的方法之一,具体公式如下:
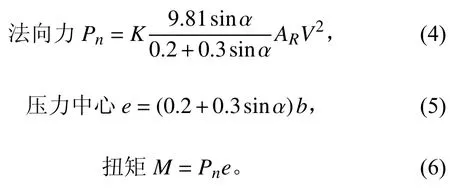
式中: α 为舵角,(°);AR为舵叶在中纵剖面上的投影面积, m2;b为舵叶弦长,m;V为水流速度, m /s;e为舵叶压力中心与舵叶前端导缘的距离,m;K为修正系数,与舵角大小、螺旋桨尾流和舵的相对位置有关。
2)模型试验换算法
模型实验换算是根据舵模试验资料来换算所需翼型的水动力系数,常用普兰特公式[11]进行换算,对NACA0018翼型以展舷比 λ=6时升力阻力系数进行换算,可以得到 λ=1.46时的升力系数和阻力系数,换算结果如表1所示。
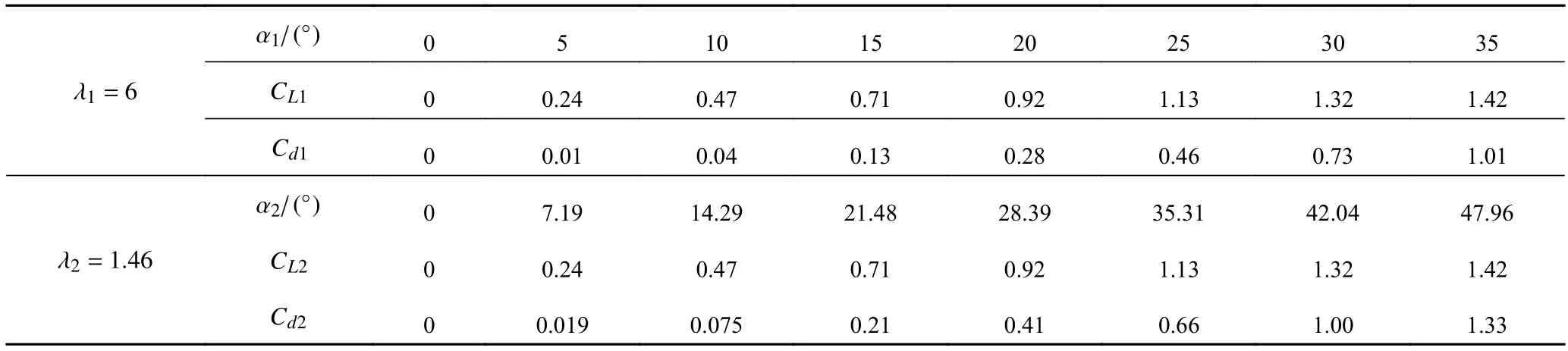
表1 λ=1.46 的换算结果Tab.1 Conversion results ofλ=1.46
3 不同翼型在CFD中的数值仿真
为了保证选型全面性,本文对NACA翼型和优化后的高效翼型进行CFD仿真计算,其中NACA翼型系列具有低阻力,高升阻比等优点,广泛沿用至今。高效翼型舵是由矩形舵后加了楔形尾后状如鱼尾而得名,经过水动力实验后发现鱼形尾部可以显著提高舵效。
3.1 矩形舵水动力性能仿真
选取剖面为NACA0018和NACA0020的2种不同厚度的舵叶翼型作为研究对象,最大相对厚度分别为18%和20%,在CAD软件中完成舵叶建模,2种翼型的展长h均为350mm,弦长b均为240mm,展弦比λ=h/b为1.46,在ICEM CFD中完成计算域设置和网格划分,划分后的非结构网格数量约为240万。
本文设置的计算域为圆柱形,如图1所示。其中流场直径为10倍弦长,将左侧边界定义为Inlet,入口设置为速度入口,流速为7.8m/s,方向垂直入口面,舵叶前端导缘与入口面距离为4倍弦长。将右侧边界定义为Outlet,出口设置为压力出口,压力为未扰动时的边界压力,舵叶后端导缘与出口面距离为5倍弦长,默认在该处流动已经充分发展。计算域的外边界距离舵叶中心线距离为5倍弦长,速度和主流速度一致,舵叶表面定义为无滑移且不可穿透的边界条件。
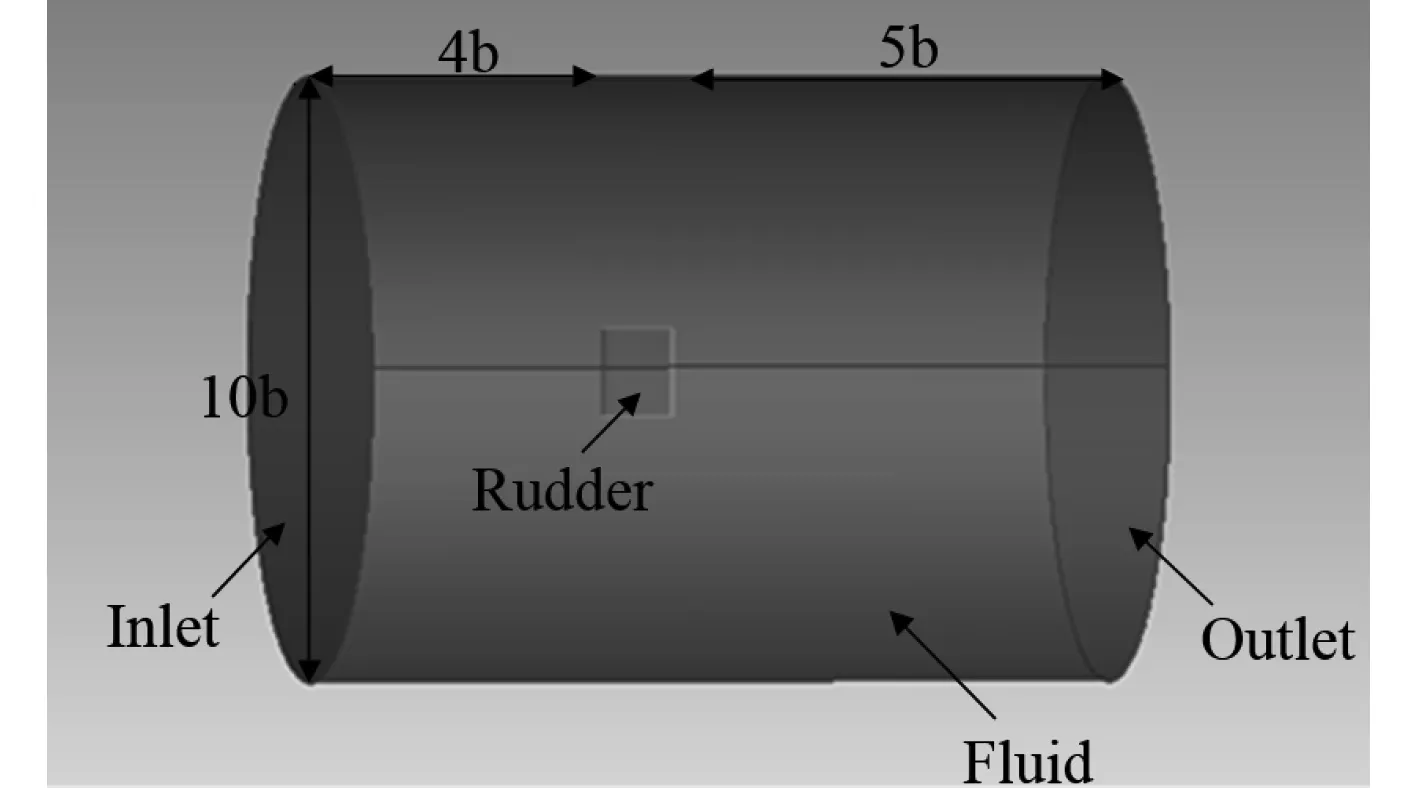
图1 矩形舵计算域示意图Fig.1 Schematic diagram of rectangular rudder calculation domain
1)如图2~图5所示,随着舵角的增大,背流面处的水流与叶面逐渐分离,NACA0018翼型在35°舵角时尾部已经产生涡流,随着舵角变大涡流半径也逐渐变大,而NACA0020翼型在35°舵角时并未产生涡流,说明相对厚度较大的翼型,产生尾部涡流的舵角较大,涡流分布范围较小,大舵角对升力的影响越小。

图2 NACA0018翼型在30°时的速度矢量图Fig.2 Velocity vector of NACA0018 airfoil at 30°

图4 NACA0020翼型在30°时的速度矢量图Fig.4 Velocity vector of NACA0020 airfoil at 30°

图5 NACA0020翼型在35°时的速度矢量图Fig.5 Velocity vector of NACA0020 airfoil at 35°
2)如图6和图7所示,随着舵角的增大,作用在舵叶表面压力中心逐远离舵缘向舵叶中部移动,涡流在NACA0018翼型背流面尾部产生的压力的明显大于NACA020翼型,压力过高会导致大舵角时的升力性能下降。

图6 NACA0018翼型在30°时的压力云图Fig.6 Pressure cloud diagram of NACA0018 airfoil at 30°

图7 NACA0020翼型在35°时的压力云图Fig.7 Pressure cloud diagram of NACA0020 airfoil at 35°
3.2 高效翼型舵水动力性能仿真
本文选用的高效翼型是在矩形舵的基础上对剖面翼型进行优化,以NACA0018翼型舵叶为母体加装鱼形尾翼改装为高效翼型,采用与NACA翼型相同的流场设置和网格划分方式,通过后处理可以得到水流作用于舵叶表面的流速和压力情况,如图8~图11所示。
由图8和图9可知,由于最大厚度更靠近舵首缘且尾部收缩剧烈,相比2种NACA翼型,高效翼型在30°舵角时背流面尾部已经出现水流分离,并且随着舵角增大尾部涡流半径也逐渐增大,导致大舵角时对升力性能的影响越大。

图8 高效翼型在30°时的速度矢量图Fig.8 Velocity vector of high efficiency airfoil at 30°

图9 高效翼型在35°时的速度矢量图Fig.9 Velocity vector of high efficiency airfoil at 35°
由图10和图11可知,随着舵角增大,翼型表面压力中心产生后移,相比与NACA翼型,背流面尾部涡流对高效翼型尾部的压力作用更加明显,对翼型尾部强度要求较高。

图10 高效翼型在30°时的速度矢量图Fig.10 Pressure cloud diagram of high efficiency airfoil 30°

图11 高效翼型在35°时的速度矢量图Fig.11 Pressure cloud diagram of high efficiency airfoil 35°
3.3 结果分析
仿真计算来流速度为7.8 m/s,对舵叶从0°~40°攻角范围内每间隔5°进行一次模拟计算,将测得的水动力系数绘制为曲线图,如图12~图15所示。
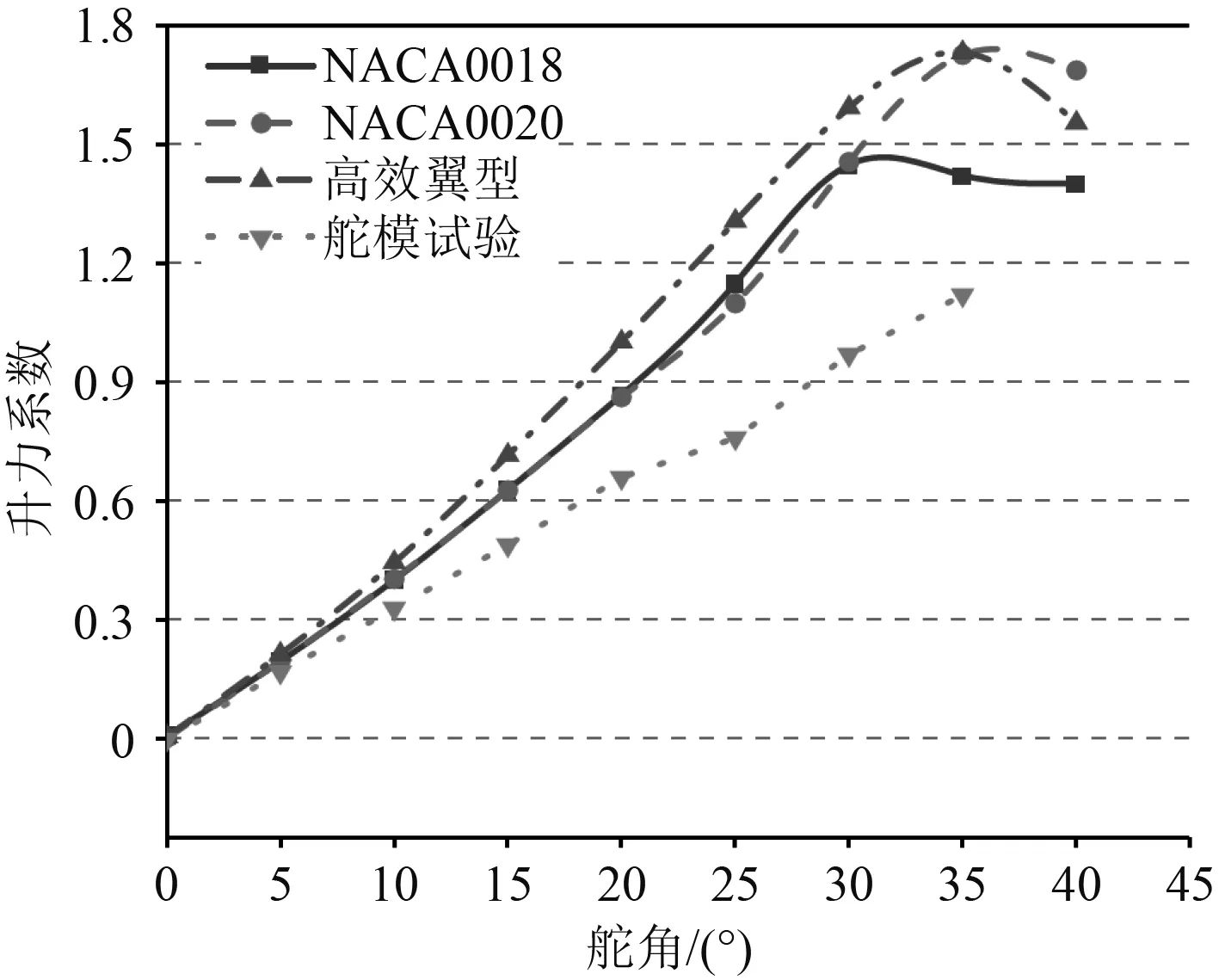
图12 升力系数对比图Fig.12 Fig, 12 Comparison of lift coefficient
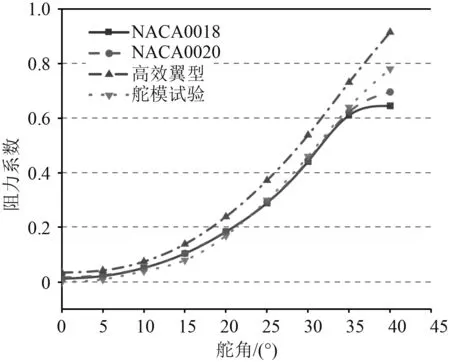
图13 阻力系数对比图Fig.13 Comparison chart of drag coefficient
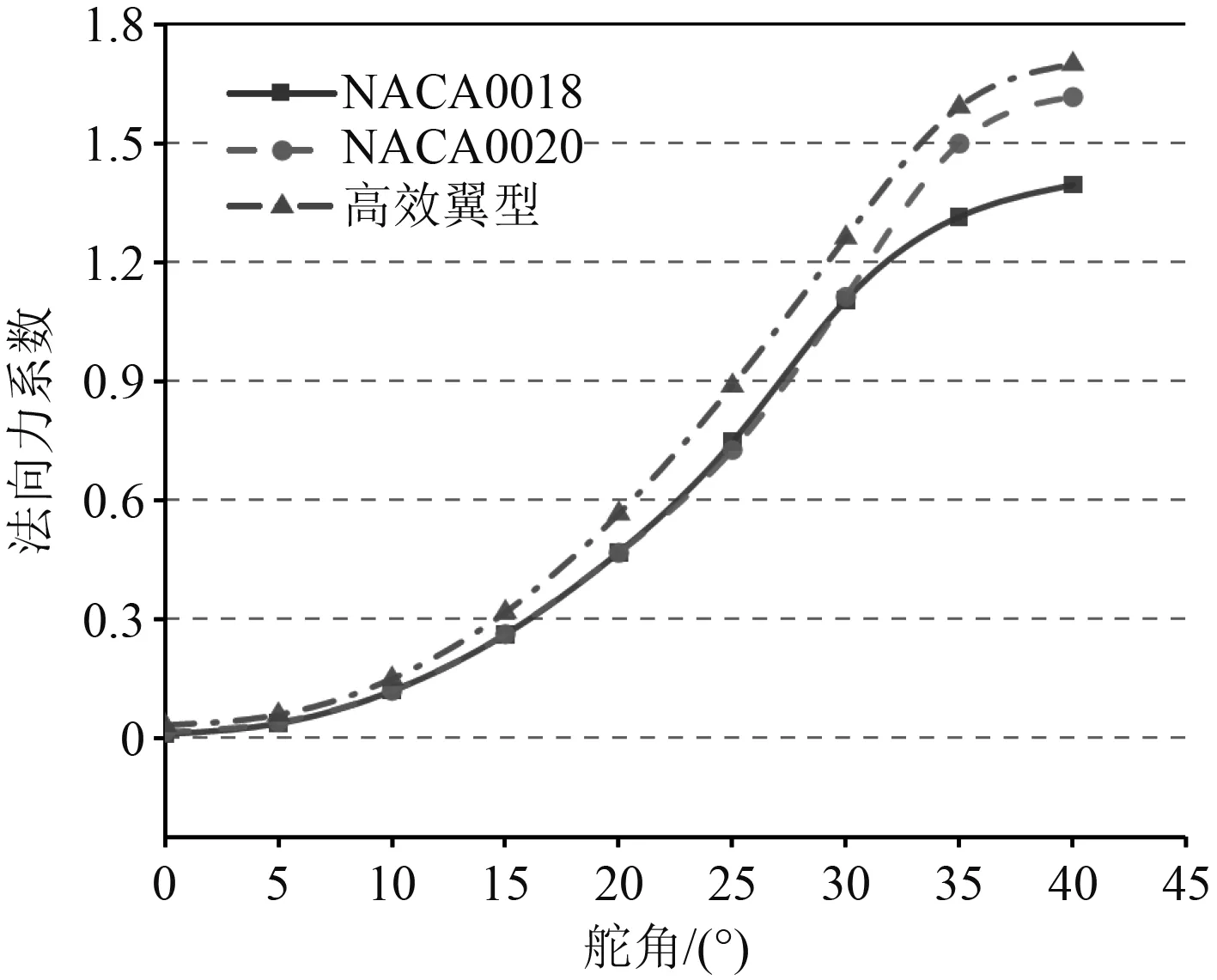
图14 法向力系数对比图Fig.14 Comparison chart of normal force coefficient
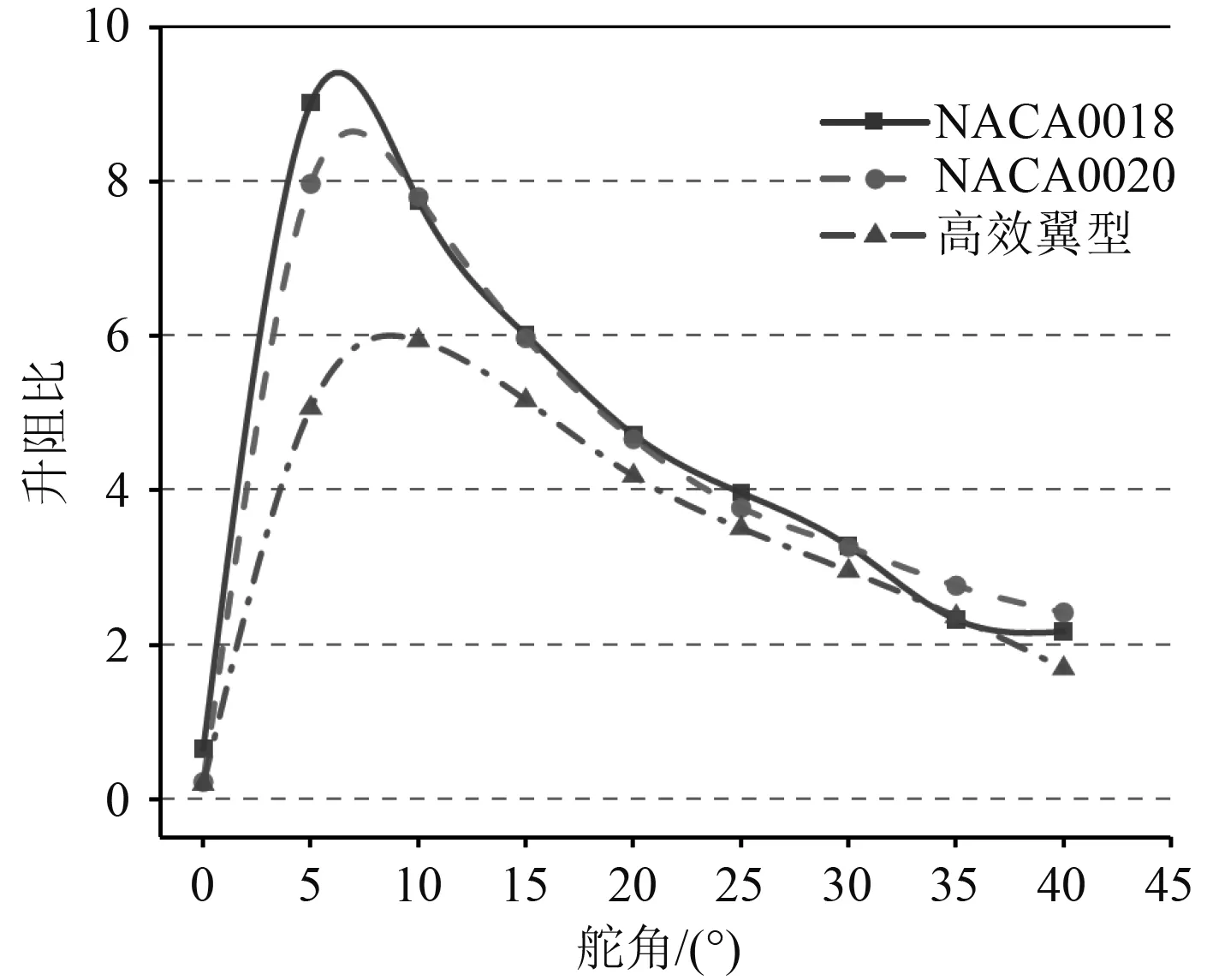
图15 升阻比对比图Fig.15 Comparison chart of lift-drag ratio
从图12和图13可以看出,3种翼型随着舵角增大升力系数先增大后减小,迎流面积逐渐增大导致阻力系数一直保持增大。在小舵角前,对不同NACA翼型升力和阻力的CFD仿真与理论计算结果误差较小,厚度比对NACA系列翼型的升力和阻力影响较小。随着舵角的逐渐增大,尾部涡流的产生对舵叶的升力产生较大影响,而对舵叶阻力未有太大影响,相比于NACA翼型,优化后的高效翼型升力提高了10%~20%,阻力提高了20%~45%,这样不能直接体现出高效舵的水动力性能优劣。
从图15可以看出,全舵角范围内NACA翼型比高效翼型升阻比平均高出25%,而NACA翼型在0°~10°范围内翼型相对厚度越大升阻比越小,30°~40°范围内,相对厚度大的翼型升阻比越大。
从图14可以看出,随着舵角的增大,高效翼型相对于NACA翼型舵效提高了15%~50%,说明高效翼型的舵效优于NACA翼型。当舵角超过30°以后,NACA0020翼型舵效比NACA0018翼型提高10%~15%,说明大舵角时,相对厚度大的翼型舵效更优。
4 翼型选用分析
舵的选型应贯穿船舶设计的总体过程,应根据船舶的总体性能要求展开。以Exploration号极地邮轮为例进行选型计算,其船舶主尺度和舵参数见表2。
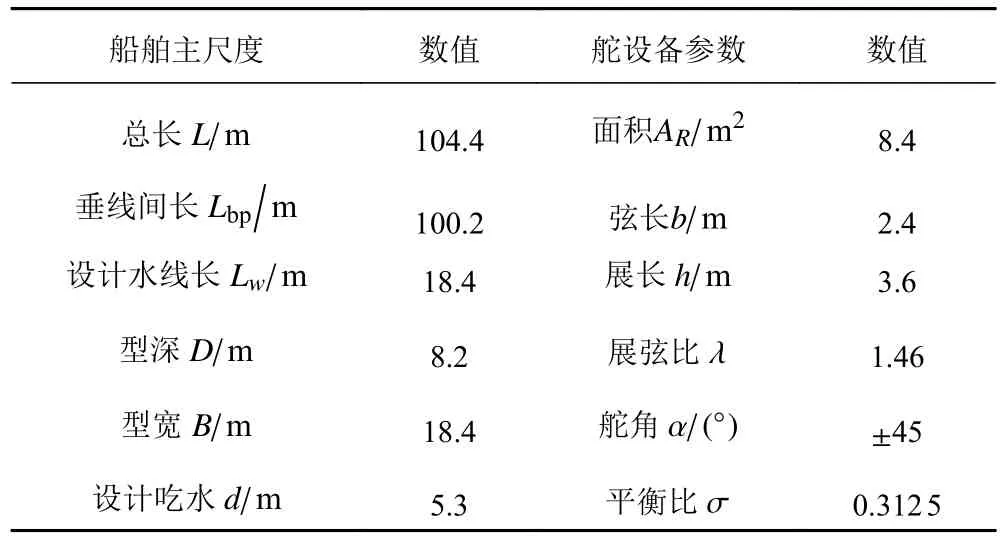
表2 Exploration号基本信息Tab.2 Basic information of Exploration
以NACA0018翼型数据作为传统方法计算的参数,通过传统方法和CFD仿真计算得到的最大舵杆扭矩见表3。
从表3可以看出,所有方法得出的舵杆扭矩均满足设计扭矩要求,水动力仿真得出的数据比公式法换算得出的舵杆扭误差更小,高效翼型的扭矩比2种NACA翼型的扭矩仿真结果更大,对船舶快速性需求更有优势,2种NACA翼型计算得到的扭矩差距不大。本文的Exploration号极地邮轮常航行在极地海域,为防止邮轮在冰区航行时由于低速而受困于冰区,要求船舶航速不得低于5 kn,并且还要频繁进出港口,因此相对于快速性而言对船舶的操纵性有更高的要求。此外航行在极地时由于浮冰作用,对舵叶表面的强度提出更高要求,因此排除高效翼型。
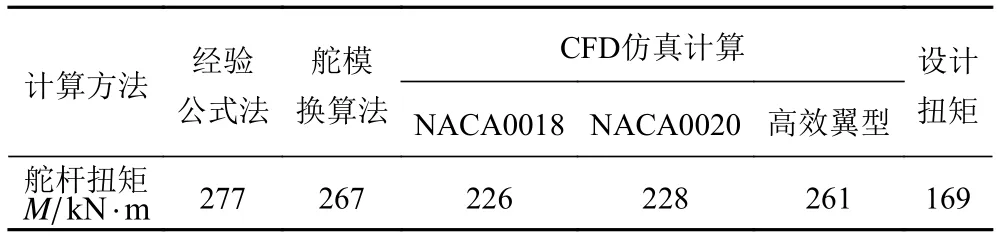
表3 最大扭矩Tab.3 Maximum torque
综合来看,NACA0020翼型在满足设计扭矩的前提下,相比于NACA0018翼型,大舵角时受尾部涡流影响较小,在舵叶背流面压力较小,水动力性能更好;相比于高效翼型,虽然升力性能略低,但是阻力却更小,升阻比更优,尾部涡流对背流面压力作用较小,更适合对操纵性和舵面强度要求高的船舶。
5 结 语
本文基于RANS方程和SSTk-ω模型对3种翼型在均匀流场中进行水动力性能仿真,根据升力系数和阻力系数对舵叶的水动力参数进行计算,并与传统方法进行对比。通过速度矢量图和压力云图对水流和舵之间的相互作用进行分析,结合实船验证得出结论如下:
1)在小舵角时,相对厚度小的翼型升阻比较大,在大舵角时,翼型厚度越大的翼型升阻比更大,涡流产生舵角大,分布范围小,可拓宽升阻比范围;
2)高效翼型在升力提高的同时,不应该忽略阻力对水动力性能的影响,由于尾部收缩较早涡流产生的舵角更小,对尾部压力作用更大,强度要求更高;
3)传统的公式计算与实际选型要求误差更大,CFD仿真则可以缩小实际误差,优化了舵叶翼型选用思路;
4)舵设备选型应综合考虑船舶整体需求,采用规范计算、CFD仿真与海试相结合的方式,在节约成本的前提下可以更能满足实际工况需求。
