基于浮动车轨迹的城市出行分析与流量预测

周 昀，丁 峰，程添亮

(1.江苏自动化研究所，江苏 连云港 222006；2.日照市公安局交通警察支队，山东 日照 276826)

1 引 言

智能交通系统是解决现代城市交通问题的主要方法。浮动车技术是基于GPS、GIS的获取道路交通信息的一种新型技术，相较于其他信息采集方法，浮动车技术采集路况信息更经济、覆盖范围广、受天气影响较小。出租车作为城市出行中最为活跃的交通工具，其行驶轨迹密度与城市人口居住密度存在较强的关联关系。通过对交通信息的定性和定量分析，能够为各种各样的交通应用提供服务。根据出租车途径路口起讫点的分布特征，我们可以刻画市民出行画像；通过预测城市特征路口过车量，能够为交通决策提供重要的参考意见。以数据为驱动的智能交通分析需要准确的行车轨迹数据和精准的地图匹配数据作为支撑，本文中轨迹数据依赖于车载GPS，地图数据依赖于高德地图。由于数据的可获取性，在已取得的成果上，本次研究提出点到点匹配与车辆行驶轨迹相结合的地图匹配方法，使用更少的地图信息，达到更精确的地图匹配。

1 文献综述

根据数据来源、数据形式、分析需求的不同，目前基于轨迹的地图匹配算法主要有几何匹配算法、拓扑关系算法、概率统计算法和先进匹配算法。在本文中则根据实际情况，我们选择了几何算法和拓扑关系算法相结合的算法。城市交通起讫点分析是监测与管理城市交通运行情况的重要一环，掌握城市交通需求方便我们采取合理的交通管控、规划方案。早先起讫点研究中的检测数据主要来自地磁、线圈等定点检测数据，Bell等、Perrakis等提出了一种基于贝叶斯估计的OD矩阵估计，结果表明模型估计和实际数据吻合度较高。曹喻旻等在车辆轨迹和定点检测器数据的基础上，提出了一种可以保证OD矩阵可靠性、计算路段流量与路段行程估计的OD估计模型。

路网交通流预测则从短时交通流的角度，对城市路况进行分析。张良力(2015)等使用ARMA模型对交叉口车辆的碰撞风险进行了评估，根据车辆进入交叉口前的速度，预测车辆进入交叉口后的速度，作为判断交叉口内车辆发生碰撞的风险依据，基于ARMA模型的预测结果能够实现车速较高精度的预测。胡浩(2019)等基于ARMA和BP神经网络的组合模型，对城市路网中的特征路口交通流进行了预测，并验证了预测效果的可行性和有效性。赵晓静(2017)等针对短时交通流的突发性、时变性和非线性等特点，基于序列分解的思想，对信号期望数据建立ARMA模型，对噪声数据进行维纳滤波处理再建立预测模型，通过组合模型实现预测结果的优化。

2 算法与模型

本文数据主体为浮动车轨迹数据和地图数据。浮动车轨迹数据来自2020年日照市五月980辆出租车GPS轨迹数据，包括轨迹点的经纬度、时间戳、瞬时速度、行车方向等信息；地图数据取自高德地图，包括路口、道路等地理位置。基于以上数据我们运用地图匹配算法刻画出租车的行驶轨迹，为分析城市通行分布与关键路口车流量预测提供数据支持。

2.1 数据准备

由于受到设备硬件和信号传播途径的限制，我们需要对收集到的数据先进行数据清洗和坐标系转换，具体步骤如下。

(1)删除重复、时间错乱、缺失、漂移等轨迹数据，其中20 s内的缺失数据用均值法进行插补。

(2)坐标转换；将浮动车GPS装置的WGS-84(World Geodetic System-84)坐标转换成GCJ-02坐标系(火星坐标系)。

(3)轨迹划分；出租车在行驶过程中，会出现换班、休息等情况，导致行车轨迹出现间隔。在起讫点问题的分析中，完整的行车轨迹是关注重点，故需要将时间间隔大、没有关联关系的轨迹进行划分，如果轨迹数据间隔超过8 h，我们认为两段轨迹不相关。

2.2 起讫点算法

算法主要功能：统计出租车每天在不同路段的通行情况。

在起讫点算法中，首先要将轨迹点与地图信息关联，对高架、快速路、复杂路口等情况，除了使用点到点地图匹配法，还要考虑历史轨迹，多条件约束下，保证路口地图匹配地准确性。其次，统计出租车起讫点通行量信息，根据统计数据分析日照市居民出行在时间和空间上的分布。考虑到出租车在城市交通中的特殊地位，其行车轨迹可用于刻画城市客流分布信息和波动规律，为进一步提高城市公共交通服务水平、增强城市公共交通智能化管理提供了一种发展方向。

算法设计过程：

(1)用点到点地图匹配算法初步获取出租测经过路口的信息；

(2)用点到线地图匹配算法和轨迹点的行驶方向、与路口相对方向对第一步得到的路口信息进行检查，进一步保证时间上相邻的轨迹点在空间上也相邻，得到最终的路口信息；

(3)针对第二步得到的结果，筛选出与路口最近轨迹点对应的地图信息，按照时间顺序确定车辆途径路口的轨迹；

(4)统计每辆车每条轨迹中途径路口的路段信息，将所有路口按照时间顺序两两匹配，得到起讫点路径对，其中算法只记录起点和终点不同的路径对。

起讫点算法流程如图1所示。

图1 起讫点算法流程图

2.3 统计学模型

本文使用统计学中的K-Means聚类和ARIMA模型对日照市出租车行驶轨迹分布以及关键路口车流量预测进行分析，K-Means是经典的快速聚类法，ARIMA模型是传统的时间序列分析方法。

交通流预测一直受到广泛的关注，基于预测可以有效地了解未来时段的交通流状态。本文通过分析特征路口车流量时间序列的内部结构特征，可推演出该路口出租车的行驶规律，最终实现路口过车辆的预测。常用的时间序列模型有ARMA(Auto-Regressive Moving Average Model，自回归移动平均模型)， ARIMA(Autoregressive Integrated Moving Average model，求和自回归移动平均模型)是ARMA的扩展，适用于分析非平稳时间序列，其表达式为

Φ(B)xt=Θ(B)εt

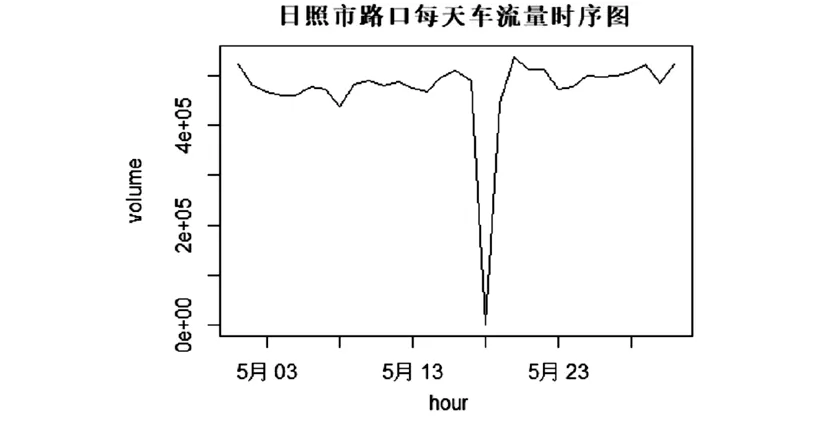
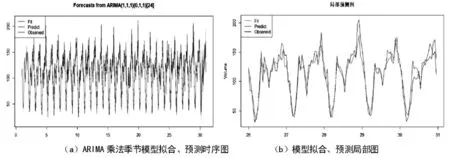
E(xsεt)=0,∀s

(1)

式中：B为延迟算子；Φ(B)=1-φ1B-…-φpBp，是自回归系数多项式；Θ(B)=1-θ1B-…-θqBq是移动平均系数多项式，模型系数求解一般使用最小二乘估计或极大似然估计。若q=0，那么AEMA(p,q)就退化成AR(p)模型；若p=0，ARMA(p,q)就退化成MA(q)模型。

使用ARMA模型时，需要先检验序列的平稳性，如果序列平稳，一般可以根据序列的自相关和偏自相关系数确定ARMA模型阶数；如果序列不平稳，需要对序列进行差分处理，提取趋势、周期等信息得到平稳序列后再建立ARMA模型，就可得到ARIMA模型。

3 实证分析

基于本次样本数据可统计出日照市路口浮动车每天车流总量和每小时的过车量，如图2所示，日照市路口出租车每日总流量在50万辆上下浮动(5月18日数据缺失，视为异常值，删除)，如图3所示序列总体呈现出较强的周期性、时变性和非线性，时间上的分布特征明显。接下来，使用K-Means聚类法和ARIMA模型分别分析日照市每日居民出行分布和关键路口车流量预测。

图2 日照市路口日流量时序图

图3 路口小时流量时序图

3.1 路口起讫点分布

为了充分考虑到节假日对城市出行产生的影响，本次研究选择2020年5月1日和5月8日为样本。综合描述性统计分析和K-Means聚类法，可得到居民出行在时间和空间上的分布为。

(1)时间上，每日出租车出行量有3个高峰，分别为上午高峰(7时～11时)、下午高峰(14时～19时)和夜间高峰(21时～22时)，说明城市交通流量分布和居民工作和娱乐出行密不可分。

(2)空间上，工作日车流量较大的区域集中在市政中心、商业区、日照市各大医院附近，节假日车流量主要集中在旅游景点、商业区和高铁站附近，存在一定的节假日效应。工作日居民的出行主要以工作、就医为主，节假日则主要以娱乐、休闲为主。

基于日照市居民节假日和工作日出行在时间和空间分布的特征，我们发现居民的出行存在一定的周期规律。由于区域或路口客流量的大幅增加会给道路通行带来巨大的压力，如果能够合理、准确地预测重要路口的过车量，为居民出行提供路况信息，可以为减缓道路通行压力提供一定的帮助。

3.2 路口过车量预测

在对城市关键路口车流量的分析中以大连路和北京南路交叉口为样本，北京南路作为日照市的重要交通枢纽，其过车量具有一定的代表性。在后面的研究中以该路口5月前30天中每小时过车量序列，预测其5月31日的每小时过车量。

图4 大连路、北京南路交叉口过车量序列分析

图4(a)表明该路口出租车的过车量呈现出明显的趋势性和一定的周期性，ADF平稳性检验后p值远小于显著水平0.05，故该序列平稳。在建模中从时间序列的随机性分析和确定性分析两个角度出发，分别使用ARIMA季节模型和Holt-Winters三参数指数平滑模型。图4(b)可知序列自相关拖尾并且包含明显的周期因素，故对序列进行一阶2步差分。

图5 大连路、北京南路交叉口过车量序列残差分析

对序列进行一阶24步差分后，序列平稳，由于原序列的长期趋势并不明显，但是存在一定的短期趋势。此处我们选择加法和乘法ARIMA季节模型、Holt-Winters三参数指数平滑模型。如图5(a)所示自相关和偏自相关系数，我们选择ARIMA(1,(1,24),)加法季节模型和ARIMA(1,11)×ARIMA(0,11)乘法季节模型进行拟合。在确定性分析中，也同样选择了加法和乘法模型，四个模型的AIC值如表1所示。

表1 拟合模型AIC值

基于AIC准则，选择ARIMA(1，11)×ARIMA(0，11)乘法季节模型描述该路口期望出租车过车量的时变性，模型如下

(2)

模型残差序列白噪声检验显示模型的残差短期内不存在相关性，模型拟合效果理想，可以接受。残差序列的方差齐性检验显示，平方残差序列不存在短期自相关性，根据图6(b)可知残差符合正态性假设且不相关，故认为ARIMA(1,11)×ARIMA(0,11)乘法季节模型可以用来刻画该序列并进行预测。

由于ARMA族模型更适用于短期序列的预测，如果进行长期预测，预测误差会逐渐变大，作为对比分别进行了6期、12期、18期和24期预测，预测效果如图6(b)所示，预测精度地评价指标如表2所示。从RMSE(均方误差)来看，6期预测的精度更高，因为随着预测期数的增加，RMSE也有一定程度地增加。由于RMSE对异常值敏感，说明超过6期的预测中，有个别点的预测误差较大，MAE(平均绝对误差)也验证了这一点，这与图6(b)的预测结果是一致的。在对预测精度要求较高的情况下，我们推荐使用短期预测。

图6 大连路、北京南路交叉口过车量序列预测结果

表2 ARIMA(1，1，1)×ARIMA(0，1，1)乘法季节模型预测精确度指标

4 结 论

本文基于出租车浮动车和地图数据，提出了一种结合点到点匹配与车辆行驶轨迹的地图匹配算法，分析了城市居民的出行分布，预测了城市关键路口过车量。目前的研究成果还有很多需要进一步深入探索的地方，例如车流量预测中只考虑了特征路口，没有对整个城市路网的车流量实现预测；ARMA族模型在非线性序列预测和长期预测上有一定地劣势，可以考虑多模型组合的方法改进，在保证预测精度的基础上，延长预测时间。希望在未来的研究中，充分融合多学科知识，为城市交通优化提供科学的方法和支持。