网联交叉口信号-车辆轨迹协同优化控制方法*

赵祥模，张心睿，王润民，徐志刚，凡海金

（1.长安大学信息工程学院，西安710064；2.长安大学，车联网教育部-中国移动联合实验室，西安710018）

前言

交叉口是城市道路的关键节点，车流在交叉口处交汇、冲突，使交叉口成为城市路网中的交通瓶颈。车联网（vehicle to everything，V2X）与智能网联汽车（connected and automated vehicle，CAV）的应用为提高交叉口交通效率、减少交通排放提供了新的解决思路［1］。V2X技术实现将网联信号灯与CAV连接为一个整体，可以显著增强车辆与道路的感知控制能力，进而实现网联信号交叉口的交通信号控制及车辆运动轨迹的优化。

围绕网联信号交叉口，部分学者研究从宏观交通层面进行交通效率优化，文献［2］～文献［5］以停车次数与交通延误为优化目标，建立交叉口交通信号优化模型。然而，仅进行交通信号控制优化不考虑车辆运动轨迹，使得车辆频繁加、减速，难以保证车辆燃油经济性与驾乘舒适性。部分学者提出从微观层面进行车辆轨迹优化。高志军等［6］提出一种基于动态距离窗的轨迹规划算法，结果表明该方法可以有效提升交叉口效率，并实现更小的速度波动；文献［7］中提出的车辆到达时序优化模型和车辆速度优化模型可有效降低车辆平均行车延误和油耗。但上述方法忽略了交通信号优化对交叉口通行能力的优化提升，且存在难以适应高密度车流环境的问题。此外，部分学者开展了车辆速度与交通信号协同优化研究。王云鹏等［8］设计了一种遗传算法-粒子群算法混合求解策略，对交通信号与车辆轨迹进行双目标协同优化，但车辆轨迹估计与优化计算相互嵌套，速度规划模型可能存在无解情况；戴荣健等［9］提出一种交通信号与车辆轨迹协同优化控制方法，仅考虑了交叉口通行效率与车辆停车次数，车辆控制分为加速与减速模型，未考虑对加速度进行优化，车辆燃油消耗难以得到优化。

针对现有不足，本文中综合考虑交叉口通行效率和车辆燃油经济性，在构建一种网联信控交叉口协同控制应用场景的基础上，研究提出一种分层解耦式网联交叉口交通信号-车辆轨迹协同优化控制方法，实现宏观交通信号与微观车辆轨迹的协同优化。

1 网联信控交叉口协同控制应用场景

1.1 网联信控交叉口场景设计

针对研究需求，本文设计了一种双向两车道的典型网联信控十字交叉口应用场景，如图1所示，场景中的信号灯与CAV均具备V2X通信能力，可实现实时交互通信。网联信号灯可以将交通信号相位及配时信息向外界广播，CAV可以将自车速度、位置等状态信息发送给处于其通信范围的网联信号灯，并实现与其他车辆的交互连接。交叉口分别有4个方向交通流：向东直行、向北直行、向西直行和向南直行。

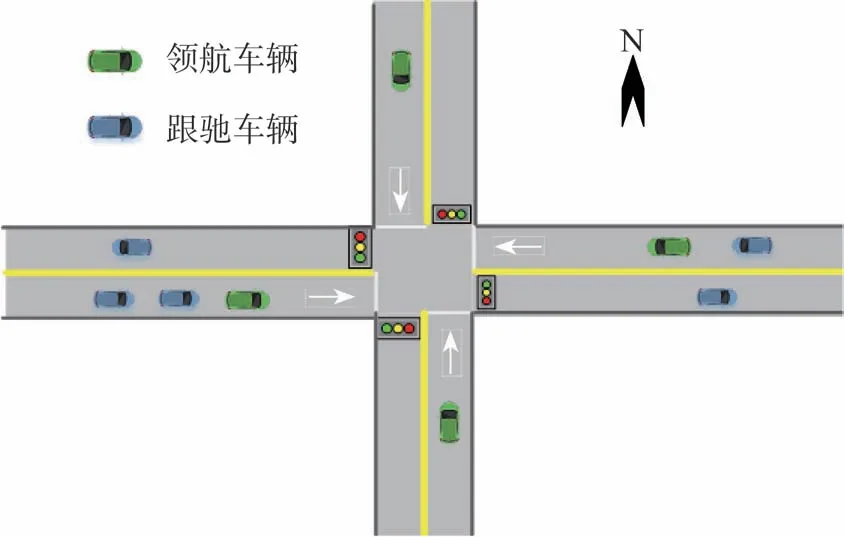
图1 双向两车道的典型网联信控十字交叉口场景

1.2 假设条件

（1）智能网联汽车假设：假设场景中所有车辆均为CAV，车辆可根据控制方案无延时地自动驾驶。

（2）通信环境假设：设定V2X有效通信范围为400 m［10］，其中网联信号的通信范围以交叉口区域中心为圆心；同时设定V2X通信为实时可靠的通信。

（3）车辆运动行为假设：假设CAV不存在换道、转向、掉头等行为，忽略轮胎及路面特性。

2 交通信号-车辆轨迹协同控制模型

交通信号-车辆轨迹协同优化控制问题具有优化变量多、模型复杂的特点，针对构建的网联交叉口场景，本文提出一种分层解耦的交通信号-车辆轨迹协同控制模型，如图2所示。网联交通信号灯获取车辆状态信息，结合交通流模型、车辆运动学模型，以最小化交叉口交通延误为优化目标，得到下一个周期最优配时及相序信息；CAV进行车辆轨迹优化，即根据交通信号优化结果，结合车辆状态信息、车辆能耗模型、车辆动力学模型，以车辆燃油经济性为优化目标，通过改变车辆速度和加速度，调整车辆行驶轨迹。

图2 网联信控交叉口协同控制模型

2.1 基于V2I的交通信号优化控制

2.1.1 临近交叉口车辆运动轨迹分析及建模

为降低交通信号优化计算复杂度，首先采用DBSCAN聚类算法［11］将车流根据行驶方向、车间距离进行聚类，形成交叉口各入口方向上车队，车辆分为领航车辆与跟驰车辆，如图1所示。将车辆运动至交叉口期间的运动轨迹划分为3段［12］，车辆在阶段1与阶段3具有恒定的加速度，在阶段2具有恒定速度，记车辆到达交叉口的时间为Tarrival，则车辆运动过程受式（1）约束：阶段1从初始位置开始，假设车辆初始车速为v0，加速度为a1，经t1时间后，行驶距离为d1，车速调整为v1；阶段2车辆以v1匀速行驶t2，行驶距离为d2；阶段3车辆以加速度a2运动，经t3后，行驶距离为d3，到达交叉口停止线，此时将车辆速度记作vf，最优情况下vf应为道路限速vmax。

式中D为车辆在初始位置时与交叉口的距离，记车辆最大制动加速度为admax，最大加速度为amax，舒适加速度为ac。

（1）领航车辆轨迹分析及建模

领航车辆是车队中第一辆车，因此根据交叉口当前交通信号信息与领航车辆行车状态，可得到车队到达交叉口的边界值。本文根据领航车辆初始位置和速度不同，将其行车轨迹分为以下2种情况。

1）车辆以当前车速到达交叉口，需要停车等待红灯。为保证车辆到达交叉口时恰好为绿灯相位，其进入交叉口前需经历减速、匀速、加速3个阶段（每阶段时长可为0），可细分为如图3所示的4种情况：

图3 领航车辆情况1下的行驶轨迹

情况1-1，车辆距离交叉口很远，在阶段3可缓慢加速，到达交叉口时达到最大车速；

情况1-2，车辆距离交叉口较远，在阶段3以最大加速度加速行驶，到达交叉口时可达到最大车速；

情况1-3，车辆距离交叉口较近，在阶段3以最大加速度加速行驶，但到达交叉口时仍未达到最大车速；

情况1-4，车辆距离交叉口很近，只经历阶段1减速阶段便进入交叉口。

图3 中，绿色实线为阶段1轨迹，黑色实线为阶段2轨迹，蓝色实线为阶段3轨迹，对应的运动约束条件如表1所示。

表1 领航车辆情况1约束条件

2）车辆以当前车速行驶，可在绿灯相位不停车通过交叉口，但损失了部分绿灯时间。为减少绿灯损失，车辆进入交叉口前需经历加速、匀速以及加速3个阶段（每阶段时长可为0），可细分为如图4所示3种情况：

图4 领航车辆情况2下的行驶轨迹

情况2-1，在绿灯开始前，车辆有充分时间进行轨迹调整，阶段3以舒适加速度加速行驶且进入交叉口达到最大车速；

情况2-2，在绿灯开始前，车辆在阶段1、3均采用最大加速度加速行驶且进入交叉口达到最大车速；

情况2-3，车辆仅经历阶段1，且进入交叉口时未达到最大车速。

图4 中，橙色虚线代表车辆以最大加速度行驶轨迹，红色虚线为车辆以初速度匀速行驶轨迹，黑色实线为车辆实际轨迹，约束条件如表2所示。

表2 领航车辆情况2约束条件

基于上述领航车辆轨迹分析，通过式（1）即可得到不同情况下领航车辆到达交叉口时间的边界值。

（2）跟驰车辆轨迹分析及建模

对于跟驰车辆，不仅受到交通灯信号的约束，还受车队中前方车辆运动状态的约束。根据与前车间运动状态关系，将跟驰车辆行车状态划分成以下2种情况。

1）最优跟驰状态，如图5中绿色轨迹所示，该状态下车辆跟驰行为可采用CACC模型［13-14］进行刻画，此时跟驰车辆应满足式（2）和式（3）。

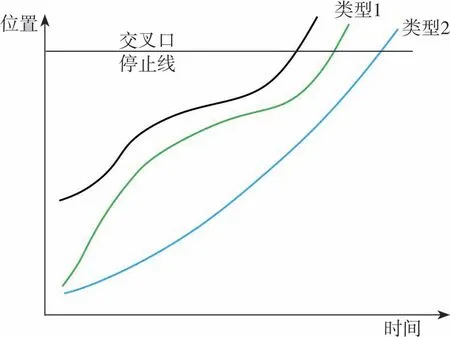
图5 跟驰车辆行驶轨迹

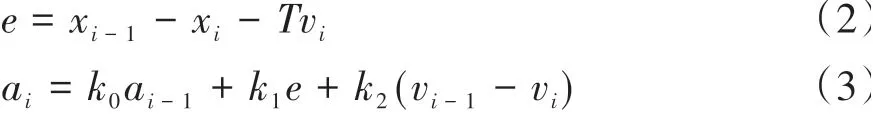
式中：xi为跟驰车辆i的位移；xi-1为跟驰车辆前车i-1的位移；vi为跟驰车辆i的速度；vi-1为跟驰车辆前车i-1的速度；ai为跟驰车辆i的加速度；ai-1为跟驰车辆前车i-1的加速度；T为车头时距；e为实际车间距离与期望车间距离的误差；k0为前车加速度项权重系数；k1为车间距误差项权重系数；k2为速度差项权重系数。

2）自由行驶状态，如图5中蓝色轨迹所示，该状态下应采用最大加速度加速行驶以减少延误，此时跟驰车辆应满足式（4）和式（5）。

2.1.2 车辆运动学模型

所有车辆应满足式（6）~式（11）所示运动学约束。

式中：x（t）、v（t）、a（t）分别为t时刻车辆行驶的位移、速度和加速度；v0为车辆初始时刻t0时速度；l和vf分别为到达交叉口停止线tf时车辆行驶的位移与速度。

2.1.3 安全约束

车辆行驶过程中，须与前车保持安全距离以避免发生事故。车辆行驶应满足式（12）约束。

式中：xi（t）为第i辆车行驶位移；xi-1（t）为第i-1辆车行驶位移；Δv为第i辆车与第i-1辆车的速度差；τ为最小车头时距；s为静止时最小车间距离，本文取3 m。

领航车辆受前方车辆队列尾车行驶状态约束，若领航车辆与前方尾车间距过近，下次聚类时将成为前方车辆队列的跟驰车辆。

2.1.4 交通信号控制模型

（1）绿灯时长约束

绿灯信号时长gs取值应满足式（13）约束：

式中gmax和gmin分别为最大绿灯时长和最小绿灯时长。

（2）信号状态约束

定义Gi为第i相位的绿灯时长，N为相位总数，Y为黄灯时长，C为周期长度，信号灯相位设计满足式（14）约束：

本文设计如图6所示十字型交叉口2相位控制结构，相位切换可由状态转换图（图7）描述，每相位的时长由车队预计通过时长与最大最小绿灯时长共同决定，如式（15）所示。

图6 十字型交叉口2相位控制结构

图7 相位切换状态转换图

式中gtravel为车队通过交叉口时长。

在上述约束条件下，车队中跟驰车辆在当前优化周期如无法通过交叉口，可在下个优化周期转变为领航车辆，与其后方车辆形成新的车队。

2.1.5 交通信号优化模型

由上述分析可得到网联信号灯通信范围内所有车队的状态（车队到达时间、通过交叉口所需时长、车队平均速度以及车队车辆数）。将这些信息作为交通信号优化输入初始状态数据，以相序和绿灯分配时长作为交通信号优化控制变量进行优化。将所有车队视为“作业”，优化问题转化为作业调度问题，因此建立以最小化交通延误为目标函数的优化模型，如式（16）所示。

式中：J表示交叉口总延误；dij为第i个进道口第j个车队的延误；Ωi为第i个进道口车队集合；ttravel为实际旅行时间；Li/vmax为自由流下旅行时间。

约束条件如式（1）~式（15）所示。

2.2 车辆轨迹优化控制

在交通信号优化的基础上，形成一个周期的交通信号配时方案。车辆轨迹优化控制问题可等价为在固定最优配时方案下最小化车辆燃油消耗的车辆轨迹控制问题。

2.2.1 车辆动力学模型

由文献［15］可知，汽车的驱动力Ft需要平衡的行驶阻力包括滚动阻力Ff、空气阻力Fw、坡度阻力Fi以及加速阻力Fj，因此汽车行驶方程表示为

式中：Ttq表示发动机输出的转矩；ig和i0分别为变速器和主减速器的传动比；ηT表示传动系的机械效率；r表示车轮半径；G表示车辆重力；f表示滚动阻力系数；CD表示空气阻力系数；A表示迎风面积；ρ为空气密度；v表示车速；δ表示汽车质量换算系数；m为汽车质量。

2.2.2 车辆能耗模型

本文采用文献［16］中所述的燃油消耗模型

式中α0、α1和α2为油耗模型系数。

根据汽车功率平衡方程式，可以得到输出功率P（t）：

2.2.3 车速最优控制模型

由于跟驰车辆受到领航车辆约束，因此在保证交通通行延误最小的情况下，调整领航车辆运动轨迹就可以实现整个车队燃油经济性的提升。固定交通信号配时下的车辆轨迹优化控制即转化为最小化领航车辆燃油消耗的优化问题。建立以最小化领航车辆油耗为目标函数的优化模型：

约束条件为式（1）~式（12）、式（17）~式（20）。

2.3 交通信号-车辆协同优化问题求解

2.3.1 基于遗传算法的交通信号优化问题求解

遗传算法是模拟生物基因遗传的做法，对群体个体按照环境适应度加以操作，实现优胜劣汰的进化过程，具有计算时间少、鲁棒性高的特点。因此本文采用遗传算法对交通信号优化问题进行求解。设计优化算法流程如图8所示，步骤如下。

图8 遗传算法流程图

（1）种群初始化。本文采用数字符号编码方式，将优化前交叉口所有车队排列顺序表示一条染色体，队列个数n表示染色体长度。

（2）适应度函数计算。本文中选择目标函数的倒数作为适应度函数。

（3）选择操作。选择轮盘赌法完成选择操作。记群体大小为s，其中个体i的适应度为fi，则i被选择的概率为

概率pi反映了个体i的适应度在整个群体的个体适应度总和中所占的比例。

（4）交叉操作。随机选择两个个体，在对应位置交换基因片段，同时保证每个个体依然是1-n的随机排列，防止进入局部收敛。

（5）变异操作。随机选择个体，同时随机选取个体的两个基因进行变换以实现变异操作。

（6）终止条件判断。如果满足终止条件，输出最优个体，即下一周期优化方案。

2.3.2 车辆轨迹优化问题求解

如2.1.1节所述，本文将领航车辆轨迹分成3段，因此式（21）可改写成式（24），此时车辆轨迹优化问题转化为包括5个变量的非线性优化问题。本文使用python最优化算法SOPT库进行求解。

3 仿真测试与结果分析

3.1 仿真环境构建与参数配置

本文基于SUMO仿真软件搭建如图9所示的仿真环境，基本仿真参数如表3所示。

图9 仿真场景

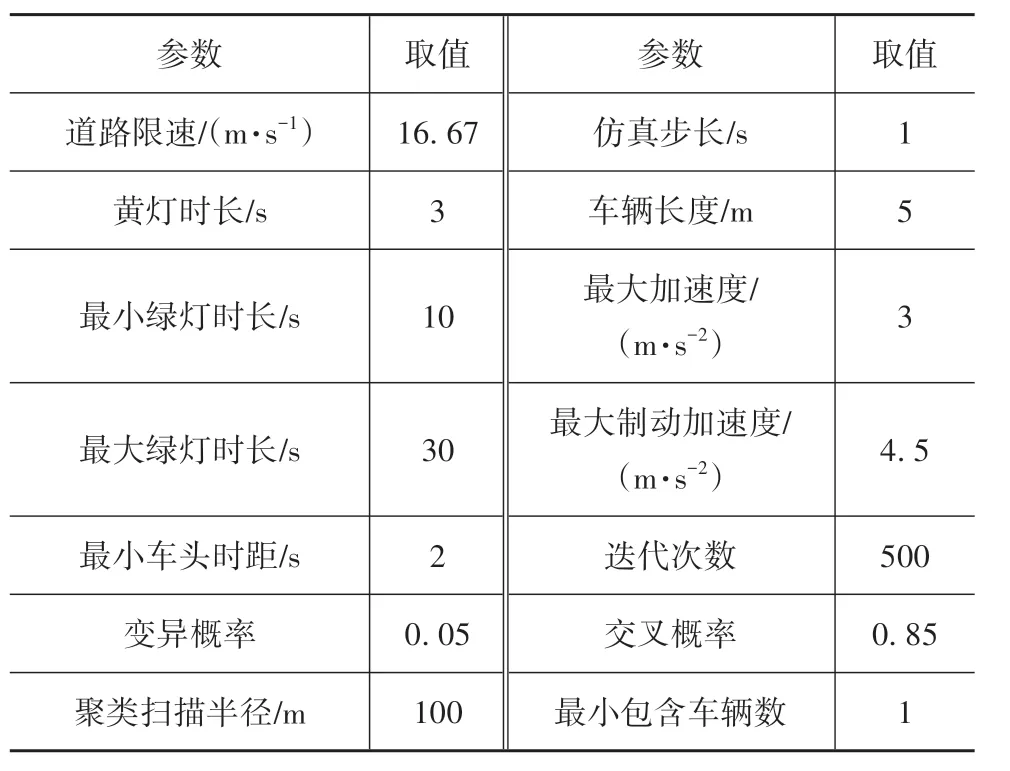
表3 基本仿真参数

3.2 测试方案设计及评价指标选取

3.2.1 测试方案设计

（1）控制方法有效性测试方案

本文采用文献［17］中所述交通流量强度描述车流量大小，交通流量强度在0.6~2.0之间为不饱和状态，在3.0~4.0之间为过饱和状态，车流量随交通流量强度增大而增大。为验证不同车流量及分布情况下提出的协同优化控制方法的有效性，设计以下测试方案。

1）测试工况1——不同交通流量工况：交叉路口各方向车流量相等，分别在0.6、1.0、2.0、3.0和4.0 5种交通流量强度工况下开展测试，以验证所提出方法在低交通流量到高交通流量的交通环境下的性能表现。

2）测试工况2——不均衡交通流量工况：将交叉路口支路划分为干线与支线，以东西方向为干线，南北方向为支线。设置干线与支线交通流量比例为1∶1、1.2∶0.8、1.4∶0.6和1.6∶0.4 4种工况，在不同工况下验证所提出方法的性能表现。

本文选择定时交通信号控制（fixed time control，FTC）、固定配时下的绿波车速引导（green light optimal speed advisory，GLOSA）和信号配时自适应控制（adaptive green light control，AGLC）方法作为对比参照。其中FTC中的交通信号按红灯33 s、绿灯30 s、黄灯3 s的方案运行；对于GLOSA，网联车辆获取信号灯数据，根据自身位置计算一个建议车速，并按照此车速行驶；AGLC根据采集车辆信息自适应调整信号配时。

（2）控制方法敏感性测试方案

为进一步分析本文提出的协同控制方法的敏感性，在不同最小绿灯时长及不同V2X通信范围条件下对本文提出的协同优化控制方法稳定性的影响进行仿真测试。

1）测试工况1——最小绿灯时长影响测试：将最小绿灯时长设置为5、6、7和8 s，在交通流量强度为0.6和3.0两种工况下，验证不同最小绿灯时长对所提出方法的影响。

2）测试工况2——V2X通信范围影响测试：将V2X通信范围分别设置为500、800和1 000 m，在交通流量强度为0.6和3.0两种工况下，验证不同V2X通信范围对所提出方法的影响。

3.2.2 评价指标选取

（1）平均旅行时间延误（average travel time delay，ATTD）：指一次仿真中，自车辆进入仿真场景起，通过交叉口并驶出的所有车辆旅行时间延误的平均值，其中，延误是指车辆在通过交叉口时由于信号控制或交通拥堵等状况导致的时间延误。

（2）平均燃油消耗（average fuel consumption，AFC）：指一次仿真中，由车辆进入仿真场景起，通过交叉口并驶出的所有车辆的燃油消耗量的平均值。

3.3 控制方法有效性测试结果与分析

3.3.1 不同交通流量下的测试结果与分析

均衡交通流量工况下的测试结果如图10和图11所示。由图可知，在不同交通流量下，本文提出的协同控制方法的ATTD和AFC值均最低：在交通流量强度为0.6时，较FTC方法，其ATTD和AFC分别下降约33%和6%；较GLOSA方法，其ATTD和AFC下降约25%和1.5%；较AGLC方法，其ATTD和AFC下降约8%和0.9%。在交通流量强度为4时，较FTC方法，其ATTD和AFC分别下降约35%和11.8%；较GLOSA方法，其ATTD和AFC分别下降约20.3%和4%；较AGLC方法，其ATTD和AFC分别下降约34%和11.4%。因此可以认为，在不同的交通流量场景下，本文提出的协同控制方法均可以有效提升交叉口通行效率和车辆燃油经济性，特别是在高交通流量下，其控制效果更显著。

图10 不同交通流量下的ATTD

图11 不同交通流量下的AFC

3.3.2 不均衡交通流量下的测试结果与分析

不均衡交通流量下的测试结果如图12和图13所示。随着干、支线道路交通流量比例差距增大，本文提出的协同控制方法优势愈加显著，其ATTD和AFC较FTC方法分别下降约65%和24%；较GLOSA方法分别下降56%和21%；较AGLC方法分别下降46%和11%。测试结果表明，FTC和GLOSA方法难以适应实际车辆到达情况，造成大量绿灯时间的浪费；而AGLC方法则缺少对车辆轨迹的优化，优化性能不佳；本文提出的协同控制方法依赖车辆到达信息的精细化感知，进行精准合理配时和行车轨迹调整，可实现交通效率和燃油经济性的显著提升。

图12 不均衡交通流量下的ATTD

图13 不均衡交通流量下的AFC

由3.3节测试结果可知，在多种交通条件下，本文提出的协同控制方法可显著提升交通效率和车辆燃油经济性，且在高密度、交通流量不均衡的交叉口环境下提升效果更加显著，表明本文提出的协同控制方法是有效的。

3.4 控制方法敏感性测试结果与分析

3.4.1 最小绿灯时长的影响分析

最小绿灯时长的影响测试结果如图14所示，随着最小绿灯时长的增大，ATTD和AFC减小幅度不断变小，即协同控制方法的性能受到最小绿灯时长的影响。最小绿灯时长由5增大到8 s，且交通流量强度为0.6工况下，ATTD和AFC的减小幅度分别由29.87%和18.7%下降到18%和11.6%；交通流量强度为3.0工况下，ATTD和AFC的减小幅度分别由16.11%和13.5%下降到7.8%和7.9%。分析原因在于较小的最小绿灯时长可避免由于交通流的波动产生绿灯时长浪费，有效提高交叉口通行效率。可以预见，若最小绿灯时长为0，即在一个周期内仅有一个方向为绿灯相位，另一相位跳过，可能会大幅度提升交通效率与燃油经济性，但这种在某一行驶方向不分配通行权的策略，违背交通公平性原则，将造成少数车辆过长时间等待，因此建议最小绿灯时长设置为5 s。

图14 最小绿灯时长对方法影响结果

3.4.2 V2X通信范围的影响分析

V2X通信距离的影响测试结果如图15所示，随着V2X通信距离的增加，ATTD和AFC减小幅度不断增大，即提出方法性能受V2X通信距离的影响。交通流量强度为0.6工况下，提出的协同控制方法的ATTD和AFC减小幅度分别由9.8%和3.3%增加到18.7%和6.9%；交通流量强度为3.0工况下，ATTD和AFC的减小幅度分别由14%和6.7%增加到26.7%和14.7%。分析原因在于随着V2X通信距离的增大，车辆将拥有更加充分的时间进行轨迹调整，从而提高交叉口通行效率和燃油经济性。对于有效通信距离的设计，不仅要考虑设备自身性能约束，还需考虑复杂交通环境的影响。但从图15可以发现，当V2X通信距离由800增加至1 000 m时，ATTD和AFC减小幅度不明显，因此认为设计V2X通信距离为800 m，可实现较优的交通效率和燃油经济性协同控制。

图15 通信距离对方法影响结果

4 结论

为了提升交叉口通行效率与车辆燃油经济性，构建了一种网联信控交叉口协同控制应用场景，并提出了一种分层解耦的网联信控交叉口交通信号-车辆轨迹协同优化控制方法，将交叉口协同控制问题转化为交通信号和网联车辆行车轨迹的分层协调优化。采用“作业调度”和遗传算法对交通优化问题进行求解；采用分段优化方法实现车辆轨迹优化简化处理。基于SUMO仿真平台的测试结果显示：本文提出的方法在均衡与不均衡的交通流量强度下，均可有效提升交通效率和车辆燃油经济性，且在高密度不均衡工况下对交通效率和燃油经济性提升更为显著；在合理的范围内，最小绿灯时长越小，V2X通信范围越大，协同控制方法的效果就越好。未来交通环境下，CAV与人工驾驶汽车混行将是一个长期的过程。混合交通流下，人工驾驶汽车受驾驶员驾驶行为的影响，会对协同优化的执行结果产生影响，因此后期有必要开展面向混合交通流的交叉口交通信号-车辆轨迹协同优化方法的研究。此外在现实情况下，V2X通信并非理想化，丢包、时延等不可靠的通信可能造成交通信号与车辆执行较期望规划存在偏差，因此需要进一步深入研究在不可靠通信环境下的网联信控交叉口协同控制方法。