基于随机数的多关节机械臂最小动力学参数集的分析研究

朱汉子, 卢剑伟, 陈新法, 尤 昕

(1.合肥工业大学 机械工程学院,安徽 合肥 230009; 2.合肥工业大学 汽车与交通工程学院,安徽 合肥 230009; 3.合肥泰禾光电科技股份有限公司,安徽 合肥 231200)

随着机械臂应用领域的增加,高速、高精度是机械臂追求的重要技术性能[1],全面掌握其动力学性能并进行精准控制是高性能机械臂研发的关键。其中,机械臂动力学参数的辨识是掌握其动力学行性能并进行控制的重要前提。但多关节机械臂动力学模型自身较为复杂,不是所有的参数都能够被辨识出来[2]。因此,从标准动力学参数中筛选确定最小动力学参数集,不仅可以降低动力学参数辨识的复杂度,还可以提高基于动力学模型的机械臂控制的快速性和鲁棒性[3]。

国外研究人员较早开始关注多关节机械臂最小动力学参数的集合问题[4]。文献[5]将动力学参数融入机械臂动力学模型中构建新的公式,利用递归的闭环关系法求解所需的动力学参数组合;文献[6]通过对机械臂动力学参数回归矩阵的分析,总结相应的动力学参数组合规则,并根据机械臂关节间的运动关系,按照组合规则确定最小动力学参数集[7]。但是上述获得最小动力学参数集的方法还有不足:一方面需要较长时间分析动力学参数的回归矩阵来确定动力学参数的组合关系;另一方面在实际应用过程中根据组合规则确定最小参数集的过程繁琐。

为此,本文在考虑关节摩擦和关节电机转动惯量基础上,首先利用MDH(modified Denavit-Hartenberg)方法建立多关节机械臂运动学模型,采用递推式牛顿欧拉方法建立其动力学模型;然后利用随机数模拟机械臂关节的运动学参数,设计了一个列变换旋转矩阵,通过该矩阵重组动力学参数的广义回归矩阵,确定回归矩阵各列的独立性和相关性;最后对重组的动力学参数的回归矩阵进行正交三角(QR)分解,从标准动力学参数中确定最小动力学参数集及其对应的最简回归矩阵。

1 机械臂动力学模型

六关节机械臂简图如图1所示。

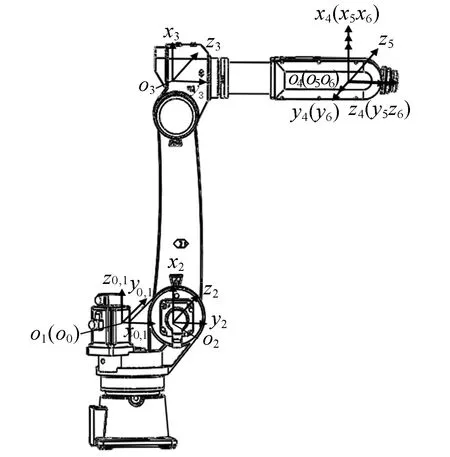
图1 六关节机械臂MDH简图

本文利用MDH方法建立其模型,并采用牛顿欧拉方法建立包含关节电机惯性量和关节摩擦在内的机械臂动力学模型[8]。

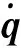
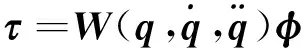
(1)

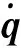
各关节电机转动惯量Ia的力矩τdriver如下:

(2)

库仑-黏滞摩擦所引起的力矩τfriction如下:

(3)

其中:fv为黏滞摩擦系数;fc为库仑摩擦系数。

以上三者是线性化的,通过线性叠加获得机器人关节力矩τall的公式[9]，具体如下:

τall=τ+τdriver+τfriction

(4)

整个机器人动力学参数φ为:

φ=[φ1φ2…φn]T

(5)

第i连杆标准动力学参数φi如下:

φi=[LxxiLxyiLxziLyyiLyzi

lxilyilzimiIaifcifvi]

(6)

其中

Lxyi=Ixyi-mirxiryi;

Lxzi=Ixzi-mirxirzi;

Lyzi=Iyzi-miryirzi;

lxi=mirxi;lyi=miryi;lzi=mirzi。

连杆i与MDH坐标系的i关系如图2所示。

图2 连杆i与MDH坐标系的i关系

机械臂的第i连杆质心Ci的转动惯量为[IxxiIxyiIxziIxxiIyyiIyziIzzi],机械臂的第i连杆质心Ci相对第i连杆MDH坐标原点oi的质心位置为[rxi,ryi,rzi]。采用平行轴定理消去机械臂动力学的非线性项,由(6)式的变量定义可得机械臂的第i连杆的质心Ci的转动惯量相对第i连杆MDH坐标原点oi的转动惯量的转化量为[LxxiLxyiLxziLxxiLyyiLyziLzzi]和质心位置的转化量为[lxilyilzi],mi为第i连杆的质量。

2 动力学参数分析

机械臂最小动力学参数集是从标准动力学参数中筛选组合出来的[10],由于并不是每一个标准动力学参数都对机器人关节力矩有影响,并且机械臂动力学参数对关节力矩的贡献值也有大小之别。机械臂标准动力学参数的可筛选组合性表明了其动力学参数对应回归矩阵空间是可以进行压缩和精简的[11]。

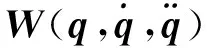
(7)

ψ∈Rm×n(m≥n)是非列满秩的矩阵,ψ的最小线性无关列组对应标准参数φ的基参数空间。最小线性无关列数也是ψ的空间维度k,而n-k列是需要删除和线性整合的。ψ的空间维度k对应标准参数φ的基参数个数,此k列贡献度最大。筛选出的n-k列对应标准参数φ中贡献度几乎为0的参数和贡献度是相关性的参数,其中,贡献度为0的参数需要删除,贡献度是相关性的参数则需要基于基参数进行线性组合。

3 列变换矩阵的求取

标准的矩阵QR分解如下:

(8)

其中:Q为m×m的正交矩阵;R为m×n的上三角矩阵。

通过对ψ进行分解求解动力学参数贡献度。由于多关节机械臂动力学参数的回归矩阵ψ是非列满秩的矩阵,对其标准QR分解不具有唯一性。但是通过Householder方式的 QR分解能够解决ψ的标准QR分解不唯一的问题[12]。于是通过列变换的QR分解使得ψ具有QR分解的唯一性,即

(9)

列变换矩阵Π∈Rn×n显示ψ各列的独立性与相关性,其中Ak、Bn-k为R的分块矩阵。

r=rank(ψ),Q为正则矩阵,Ak为k×k的上三角非奇异矩阵,rank(ψΠ)=rank(Ak)。由Householder矩阵H1,…,Hk和变换矩阵Π1,…,Πk可得:

(H1,…,Hk)ψ(Π1,…,Πk)=R=

(10)

令C(m-k)(n-k)=[zk+1,…,zn],其中参数zj为C的各列,令‖zp‖2=max(‖zk+1‖2,…,‖zn‖2),其中j=k+1,…,n。如果rank(Ak)=k,那么‖zp‖2就等于0。于是,该变换矩阵Π的设计方法如下:

广义矩阵ψ初次QR分解,对初次分解获得R矩阵的对角线数值的非零值对应的列位置和零值对应的位置进行标记,根据标记位置构造列变换原矩阵Θ,然后对n阶单位矩阵进行Θ列变换来构造列变换矩阵Π。

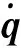
(11)

令E为m×n的单位矩阵,该随机数下的广义矩阵的旋转矩阵p为:

p=ΘE

(12)

4 基参数及参数线性组合

利用(12) 式列变换矩阵p可得:

(13)

其中:φ1为基参数;φ2为基于基参数的可线性组合的参数。

将ψ进行列变换,可得k个独立的列矩阵ψ1和n-k个需删除、组合的列矩阵ψ2:

ψrandomp=[ψ1ψ2]

(14)

对 (14) 式随机广义矩阵ψrandom进行列变换后,对ψrandomp进行QR分解,可得:

[Q1RkQ2Rk×(n-k)]

(15)

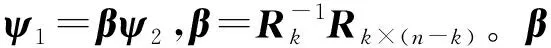
φmin=φ1+βφ2

(16)

最小参数集φmin及其对应回归矩阵ψ1与标准动力学参数φ及其对应回归矩阵ψ关系如下:

ψφ=ψ1φmin

(17)

5 求解与验证

通过数值算例验证本文提出方法求解的最小动力学参数集的正确性和有效性,机械臂的MDH参数见表1所列。

表1 机械臂MDH参数

应用本方法得到的机械臂最小动力学参数集的符号组合解如下:

Lzz1+Lyy2+Lyy3+0.487lz2+0.300 2lz3+

0.592 9m2+0.209(m3+m4+m5+m6),

Lxx2-Lyy2-0.186(m3-m4-m5-m6),

Lxy2,

Lxz2-0.431 8lz3+0.040 3(m3+m4+m5+m6),

Lyz2,

Lzz2+0.186(m3+m4+m5+m6),

lx2+0.431 8(m3+m4+m5+m6),

ly2,

Lxx3-Lyy3+Lyy4+0.866 2lz4+

0.187 1(m4+m5+m6),

Lxy3-0.020 3l4z-0.008 8(m4-m5-m6),

Lxz3,Lyz3,

Lzz3+Lyy4+0.866 3lz4+0.188(m4+m5+m6),

lx3-0.020 3(m4-m5-m6),

ly3-lz4-0.433 1(m4-m5-m6),

Lxx4-Lyy4+Lyy5,

Lxy4,Lxz4,Lyz4,

Lzz4+Lyy5,lx4,

ly4+lz5,

Lxx5-Lyy5+Lyy6,Lxy5,

Lyz5,Lzz5+Lyy6,lx5,

ly5-lz6,

Lxx6-Lyy6,Lxy6,Lxz6,

Lyz6,Lzz6,lx6,ly6。

因为摩擦项和电机转动惯量项参数不能精简,为了保证机械臂动力学模型的完整性,本文将其纳入建模之中,所以原有各连杆参数有[LxxiLxyiLxziLyyiLyziLzzilxilyilzimi],其中i=1,…,6,参数总量为60个。本文方法去除连杆1中的Lxx1,Lxy1,Lxz1,Lyy1,Lyz1,lx1,ly1,lz1和连杆6中的lz6,最后通过线性组合成上述的最小动力学参数集的36个符号组合解结果,同时在CORE I5 CPU 上求解该六关节机械臂的最小参数集用时为3.64 s。

为验证该方法的最小参数集在动力学上的准确性与有效性,利用Matlab软件里robot tools模块建立该机械臂模型如图3所示,设计的圆弧轨迹如图4所示。

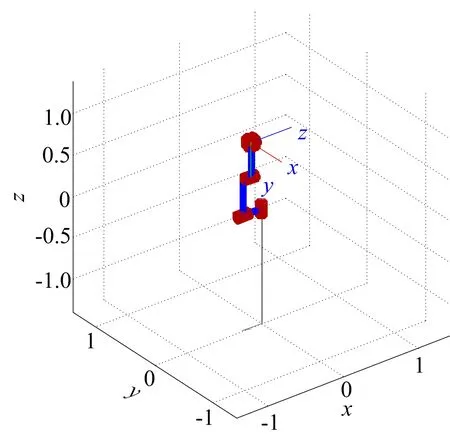
图3 机械臂结构

图4 机械臂轨迹

该软件模块获得圆弧轨迹下各关节运动变量,其中机械臂第3关节的角度、角速度和角加速度如图5所示。对比简化前与简化后机械臂的各个关节的力矩值,如图6所示。

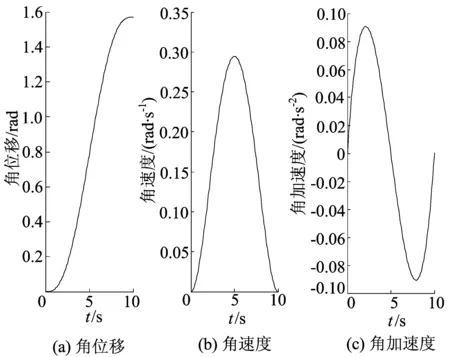
图5 机械臂的角位移、角速度和角加速度

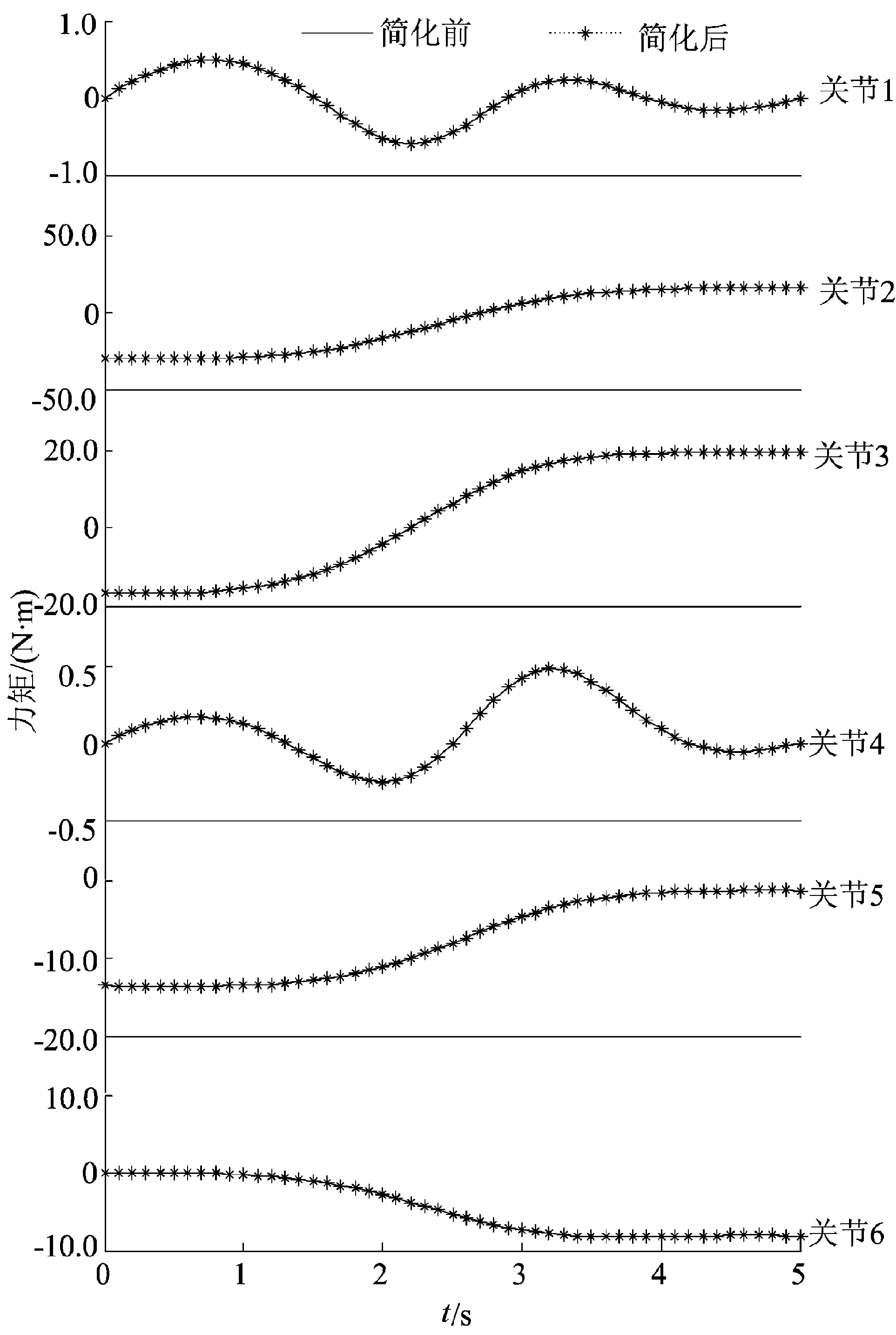
图6 模型简化前与简化后力矩对比

通过Adams建立的机械臂仿真模型,采用有限项傅里叶级数获得辨识激励轨迹,利用最小二乘法辨识六关节机械臂的前3个关节的最小动力学参数集，并计算前3个关节的关节力矩,与Adams仿真出的该激励轨迹下的前3个关节力矩对比如图7所示;3个关节的仿真力矩与辨识力矩误差值如图8所示。

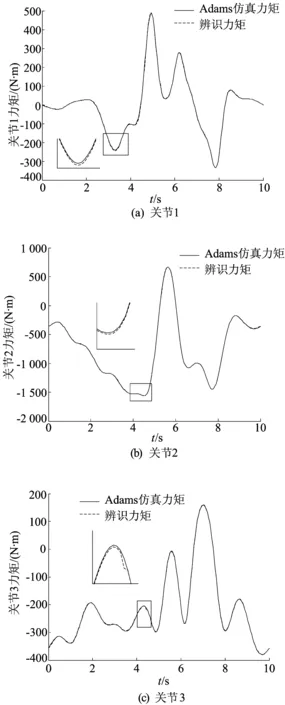
图7 关节力矩Adams仿真与辨识计算力矩

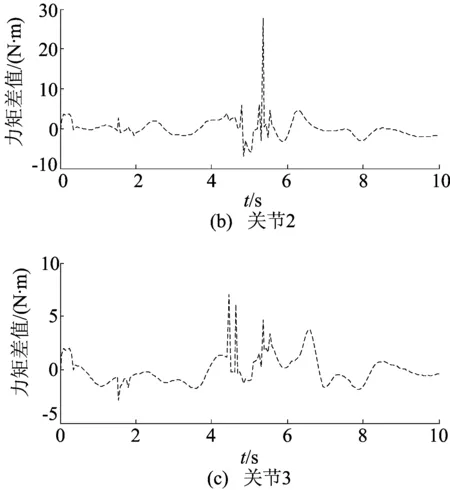
图8 关节力矩Adams仿真值与辨识计算值误差值

通过以上2种方式对比,本文的最小动力学参数集计算方法完整反映出原有机械臂动力学特性;同时通过辨识结果分析可知,该方法计算的最小动力学参数集有较好的辨识性。

6 结 论

为了求取多关节机械臂最小动力学参数集,本文利用生成的随机数模拟多关节机械臂运动参数,设计一种回归矩阵的变换矩阵,从而在较短时间内确定最小动力学参数集。以六关节机械臂为例,通过数值算例对所提出的方法进行了验证,结果表明,本文提出的方法获取的最小动力学参数集准确有效,所提出的最小动力学参数计算方法稳定、可靠。