协变量缺失下集值映射多目标规划模型仿真

吴功跃，周香花

(南昌大学科学技术学院，江西南昌330047)

1 引言

自从多目标规划问题被提出，就普遍存在并广泛应用于交通运输、资产负债管理、金融投资、军事科学等众多领域中，这些领域均在经济、军事以及日常生活中起着重大的决策作用，且占据着举足轻重的地位[1]，因此，各类多目标规划模型应运而生。该模型凭借对当中层次关系的恰当描述、对决策者意愿的全方位展示以及将社会生产实际问题作为规划根本等诸多优势，不断拓宽应用前景，提升应用价值。针对多目标规划模型的实际应用背景，许多相关学者与研究人员都对其展开了深入探索。

例如，谢仕炜等人[2]以通信领域主动配电网为研究对象，设计出一种不确定随机网络理论的多目标规划模型，经架构不确定随机主动配电网，完成经济最小化与最小生成树搜寻的目标设定，采用三维不确定机会空间解得多目标规划问题；文献[3]提出的PSO-GRA耦合决策下排水沟系统多目标规划模型中，利用粒子群算法获取非劣解集，结合灰色关联投影法选择最终决策；文献[4]以运输行业为研究背景，将模糊变量设定为供应链的风险与绩效，构建出一种模糊动态非线性多目标规划模型，设立成本、风险最小化与绩效最大化目标后，综合考虑供应商、订单分配、风险以及绩效等因素，得到模糊动态非线性多目标规划模型，利用模糊评价法实现模型的处理与计算。

因上述各文献模型中未考虑到数据缺失情况，导致规划结果存在一定的偏差，为此，本文以协变量缺失为前提条件，提出一种集值映射多目标规划模型。通常在采集数据过程中，因某些因素造成只有部分数据得到观测(比如问卷调查阶段，被调查者由于问题涉及个人隐私而未给出答案)，由此便产生了数据缺失现象。为解决数据缺失带来的误差与错误推断，引入示性随机变量，令协变量为随机缺失，根据协变量缺失情况，实现参数与非参数的经验似然推断，减小规划误差，增强模型鲁棒性。

2 协变量缺失下集值映射多目标规划模型构建

2.1 模型建立及约束条件确定

利用一个上层决策者(即领导者)与多个独立且平行的下层决策者(即跟随者)，构建集值映射多目标规划问题的数学模型。跟随者在领导者做出决策后，根据领导者的决策知识来最小化其目标函数，领导者再制定出对其目标函数具有优化作用的决策。值得指出的是，该多目标规划模型的决策过程存在一定的交互性[5]。

设定下层决策者数量是n个，领导者在给出决策之前有充分考虑到跟随者的反应，且选择的决策结果是以跟随者决策为基础，其表达式如下所示

(BLMOP)1=minQ(x，y1，…，yn)

(1)

下列方程组为对应约束条件

(2)

通过上式可以看出，领导者最优决策的制定复杂程度随着跟随者提供决策范围的不断缩小而降低，且有可能等同于下层问题中部分有效解相对应的目标函数值。综上所述，用目标函数值集Ti(x)代替最优反应集Ei(x)是可行的，因此，由(BLMOP)1表达式推导出的下列多目标规划模型

(BLMOP)2=minG(x，z1，…，zn)

(3)

对应约束条件式如下所示

(4)

基于该多目标规划模型，领导者目标函数用G:A*T1(x)*…*Tn(x)→Y表示。基于各类导数概念与集值优化问题[6]的关联结果，令下列方程式成立

F(x)={G(x，z1，…，zn):zi∈Ti(x)，i=1，2，…，n}

(5)

其中，集值映射是F:A→2Y，并基于此将(BLMOP)2改写为下列表达式

(BLMOP)3=minF(x)

(6)

此多目标规划模型的约束条件方程组如下所示

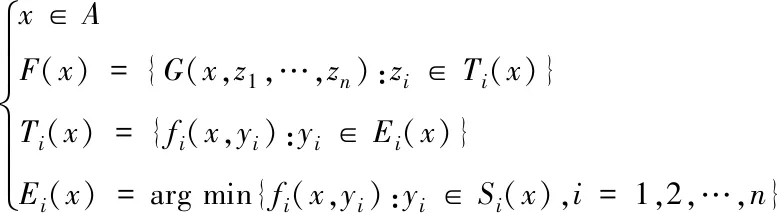
(7)

此时，令x0∈A、yi0∈Si(x0)、zi0=fi(x0，yi0)、z0=G(x0，z10，…，zn0)成立。

当满足(F(x)-z0)∩{-intC}=∅与yi0∈Ei(x0)时，(BLMOP)3的弱有效解[7]为(x0，y10，…，yn0)。其中，∀x∈A。

2.2 模型参数经验似然推断

设定规划模型的随机样本为{Yi，Xi，Ui，Zi}，可完全观测到的样本是(Yi，Xi，Ui)，而缺失的协变量则是Zi。利用示性函数技术[8]，引入随机变量δi，令协变量为随机缺失，且满足下列条件式，推导出式(9)

(8)

P(δi=1|Yi，Ui，Xi，Zi)=P(δi=1|Yi，Ui，Xi)

=π(Yi，Ui，Xi)

(9)

上式表明，已知Yi，Ui，Xi时，δi与Zi均具有独立性，选择概率函数为π(Yi，Ui，Xi)。

基于协变量Zi缺失情况与逆概率加权方法[9]，利用下列逆概率加权目标函数，实现分量参数β的最小化估计

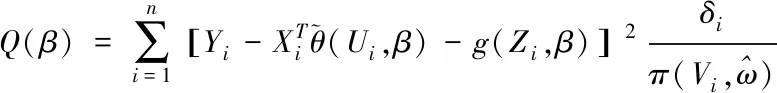
(10)

综上得出分量参数β的辅助随机向量表达式，如下所示

(11)

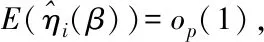
(12)

采用拉格朗日乘子法[11]计算分量参数的经验似然比函数，得到下列解方程表达式

(13)

式中，拉格朗日乘子为λ，界定公式如下所示

(14)

2.3 模型非参数经验似然推断

若已知随机样本Ui的密度函数是f(u)与分量参数β，且满足下列表达式

E{X[Y-g(Z，β)-XTθ(u)]}=0

(15)

假设核函数K1h1的带宽是h1，则非参数θ(u)的辅助随机矢量与经验对数似然比表达式分别如下所示

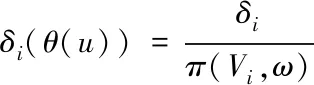
(16)

由于此函数不属于标准的卡方分布[12]，故构建下列残差调整下辅助随机矢量表达式

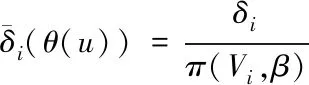
(17)

因此，采用下列表达式界定非参数θ(u)的残差修正经验对数似然比

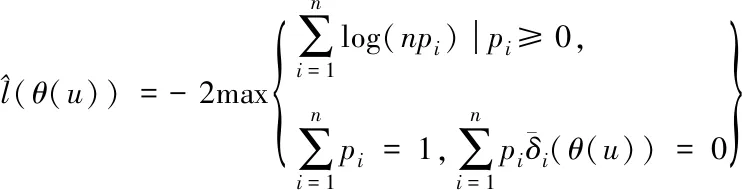
(18)

3 集值映射多目标规划模型仿真分析

协变量缺失下集值映射多目标规划模型的仿真结果通过C#编程软件获得，实验环境主要采用因特尔I5 3516型号4.2GHz处理器，内存为8GB。为验证模型有效性，降低随机性对模型结果产生的影响，分别采用文献[2]、文献[3]、文献[4]方法以及文本所建模型展开以下仿真。

3.1 协变量缺失下模型经验似然检验效果

图1所示为样本函数取不同数值(100、150、200)、显著性水平是0.05时的经验似然比检验结果。

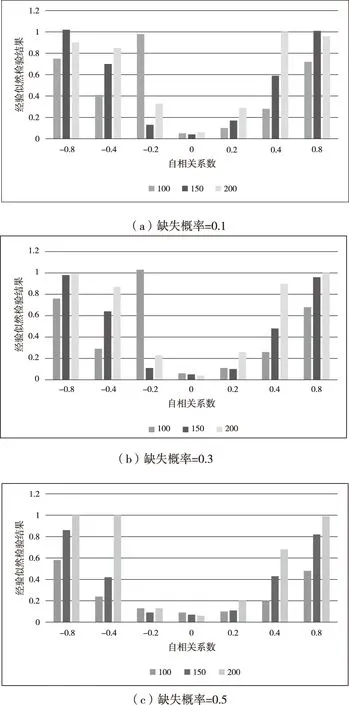
图1 不同缺失概率下经验似然检验结果

根据图1中的经验似然检验仿真结果可以看出：关于不同样本函数取值，数值越高，经验似然检验越趋近于1，说明经验似然检验效果与样本函数值之间呈正相关关系，检验功效随样本函数值的增加而更优，这是因为本文引用逆概率加权方法，最小化估计了分量参数，构建出对应的经验似然比函数，并采用拉格朗日乘子法求取解值；针对缺失概率与经验似然检验结果关系，一般情况下，显著性水平将随着协变量缺失概率的不断上升而逐渐偏离预设值，而本文方法因利用示性随机变量，进一步假设了协变量为随机缺失，经结合协变量缺失情况，使上表中数据与预设值较为拟合，大幅提升了经验似然检验性能。综上所述，本文提出的经验似然推断方法能够对协变量缺失下集值映射多目标规划模型的经验似然做出有效验证，具有较好的合理性与可靠性。

3.2 集值映射多目标规划模型性能评估

设定模型决策变量分别是5维与10维，验证模型的有效性。通过运行各模型10次，对比运行结果相关性能，得到的性能指标结果为各层函数的最优、最差以及中等函数评估次数，还有由目标函数取得的精准度、下层被执行次数以及执行时的下层函数评估次数均值，具体数值如列各表所示。

通过表1中10次运行评估指标数据可以看出：文献提及的各类多目标规划模型下层最优函数评估次数分别是本文模型的5.48倍、7.72倍、6.88倍，上层分别是本文模型的8.53倍、7.3倍、7.98倍；针对下层中等函数评估次数，分别是本文模型的6.08倍、7.19倍、7.01倍，上层分别是本文模型的4.6倍、4.11倍、4.24倍；而下层最差函数评估次数则分别是本文模型的7.23倍、7.32倍、6.99倍，上层分别是本文模型的6.17倍、6.86倍、6.43倍。这是因为上层决策者将下层决策者的反应作为考虑因素，且下层决策者提供决策范围的不断缩小大幅降低了上层决策者的最优决策制定复杂程度，使得本文模型不必参与过多的函数评估，在一定程度上减少了评估次数。

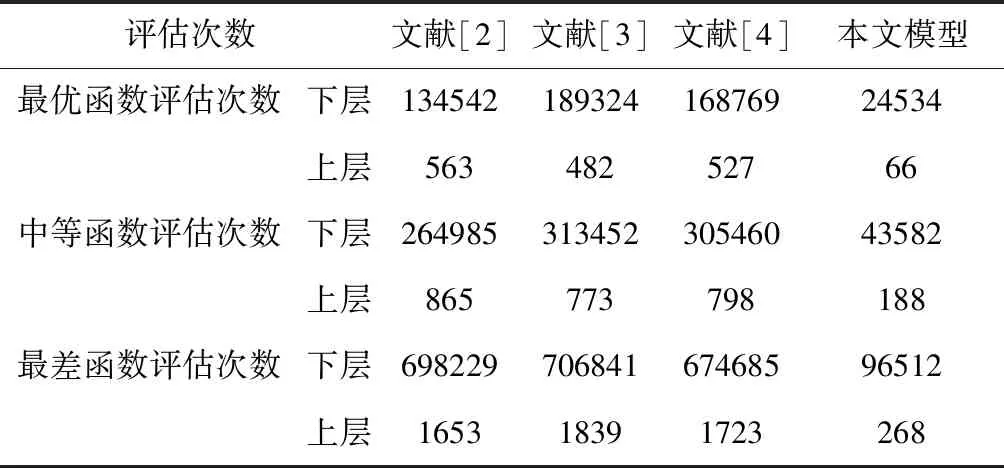
表1 5维多目标规划模型各层函数评估次数统计表

由表2数据可知：尽管本文模型与文献方法的上层中值目标函数精度差异较小，但下层精度对比文献模型更理想，且其中值下层被执行次数也仅有各文献模型的0.27～0.28倍，由于对协变量缺失下模型经验似然做了推断，加快了模型的收敛速度，所以，在一定程度上降低了下层函数评估次数。

表2 5维多目标规划模型各层目标函数相关指标统计表

从整理得到的表3评估次数发现：各层函数评估次数均随着决策变量的增加而大幅上升，与此同时，文献各模型出现了不同程度的失效现象，比如文献[3]几乎完全失效，文献[4]在执行最差函数评估时失效，只有文献[2]模型与本文模型完成了所有评估，但经过对比可知，本文模型的各级函数评估次数因持续缩小跟随者决策范围而具有较大优势，仅是文献[2]模型各层评估次数均值的0.12倍与0.28倍。

表3 10维多目标规划模型各层函数评估次数统计表

从表4各层目标函数相关指标数据可以看出：本文模型的各层中值目标函数精度均优于文献方法，其平均调用下层问题次数也因经验似然推断阶段，极大程度小于各文献模型。

表4 10维多目标规划模型目标函数相关指标统计表

4 结论

本文针对实际数据收集过程中存在的数据缺失问题，构建出一种基于协变量缺失的集值映射多目标规划模型。尽管目前已经取得了一定的研究成果，但仍需在以下几个方面做出改进：关于多目标规划模型的异方差检验与序列相关检验等问题，应继续进行进一步的探讨；逆概率加权方法稳健度不足，在今后的工作中，应尝试结合线性加权、降维等更优越的算法与策略，获取协变量缺失下更稳健的估计值，并在一定程度上降低运算复杂度；因时间关系，实例应用研究的实验对象较为单一，应将模型应用于多个实际问题中，通过发现更多问题，完善模型性能，提升模型实用性与通用性；将多目标规划模型的最优性条件研究作为下一阶段的研究重点，以最优性条件作为基础，进一步提升运算效率与收敛速度。本文成果为多目标规划模型理论与方法的发展指明了方向，为优化与决策等问题的处理奠定了坚实的理论基础。