基于热泵热量传递系数预测的PV/T-SAHP系统建模

李畸勇，周兴操，王纪港

(1.广西大学电气工程学院，广西 南宁 530004；2.广西电力系统最优化与节能技术重点实验室，广西 南宁010020)

1 引言

太阳能属于可再生能源，总量丰富且覆盖范围广。近年来，太阳能使用规模的逐步扩大加快了相关产业的技术升级，将太阳能应用于我国的建筑用能领域也大有推广之势[1]。但受制于材料物理性能限制，包括单晶硅、多晶硅在内的光伏(PV)组件对太阳能的转换率仍低于20%，太阳照射带来的温升还将进一步降低其发电效率[2]，故集发电、蓄热功能的光伏光热一体化热泵(PV/T-SAHP)系统受到了人们越来越多的关注[3-4]。

PV/T-SAHP系统主要包括光伏光热(PV/T)组件、集热水箱、热泵、蓄热水箱等，整个系统的运行直接受到天气情况变化的影响。对PV/T-SAHP系统进行建模，不仅便于进行性能研究，还可用于设计各类优化控制策略，实现太阳能的高效利用。目前，对PV/T-SAHP系统的建模方法大致分为两类：其一，借助各种仿真软件进行模拟。John Clauß[5]利用建筑性能软件(BPS)研究了热泵建模的复杂度对能效和热泵运行等关键性能指标的影响。Francesco Reda 和Satu Paiho[6]在TRNSYS软件中比较了太阳能辅助吸收式热泵及光伏驱动空气源热泵两种PV/T-SAHP系统的供热节能性能。受到PV/T-SAHP系统种类不同的影响，仿真软件难以做到较高适用性，精确度也有待提高。其二，进行热力学分析，建立复杂的数学模型。裴刚，季杰[7]提出的PV/T-SAHP系统模型包括PV/T模型和热泵热力循环模型两部分。该模型可以模拟在全天过程中PV/T-SAHP系统性能参数的动态变化，可用于分析PV/T模块的面积、倾斜角、管间距等参数对系统性能的影响，便于系统的优化配置。张政[8]针对光伏太阳能热泵/环形热管(PVSA-HP/LHP)复合热水系统建立数学模型，对该系统在热泵(HP)模式独立运行、环形热管-热泵(LHP-HP)复合模式运行下的性能进行对比模拟。上述两篇文献均采用微元法对系统进行建模，考虑了制冷剂在热泵中液相、气相、气液两相等三种不同的工作状态。模型构成十分复杂，求解需不断迭代并且及时更改所设定的冷媒蒸发温度，耗时过长导致难以应用于实时优化控制系统的设计。

为此，本文首先利用Elman神经网络预测出热泵的热量传递系数[9]，等效热泵复杂的热量传递过程，大大降低了PV/T-SAHP系统的建模难度。然后采用集总参数法[10]对PV/T-SAHP系统进行建模。最后通过实验验证了该模型预测结果与系统真实运行情况基本一致。

2 PV/T-SAHP系统介绍

本文研究的是水冷式PV/T热泵系统，如图1所示，通过控制器控制水泵将集热水箱中的冷却水泵至PV/T组件并不断循环，在积聚热量的同时降低了PV/T组件的温度。当集热水箱的水温上升到一定值，其降温效果显著下降。此时须开启热泵，一方面可将集热水箱中的热量转移至蓄热水箱中储存以满足日常热水需求，另一方面也可降低集热水箱中水温保证降温效果。PV/T-SAHP系统可大幅提高光伏板发电效率，实现电能与热能的综合利用。

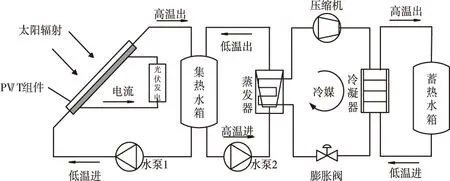
图1 PV/T-SAHP系统示意图

由图1还可知，蓄热水箱从冷凝器处获得的热量与蒸发器处从预热水箱带走的热量直接相关。本文将同一采样周期内蓄热水箱获得的热量与蒸发器处转移的热量之比定义为热泵热量传递系数K。

3 热泵热量传递系数预测

3.1 热泵热量传递系数预测因子的选取

本文的实验地点选在广西南宁地区(东经108.3° 北纬22.8°)，组件正南朝向，22°倾角放置，通过校园气象站采集气象数据，包括太阳辐照度(Gr)、环境温度(Thj)、环境湿度(Hhj)、风速(Ws)，通过光伏光热监控系统采集水泵2频率(fsb)。此外，该系数还应存在时间序序列上的自相关性，故本文另选取预测时刻前两个时间序列数据K(t-2)、K(t-1)来分析该自相关性，时间间隔为20s。相关系数r的计算公式如下

(1)

晴天条件下，上述变量的相关性结果如表1所示。

表1 晴天条件下各预测因子的相关系数

多云条件下，上述变量的相关性结果如表2所示。

表2 多云条件下各预测因子的相关系数

由表1和表2可知，晴天及多云条件下，各因子相关系数稍有不同，但整体相关趋势相同，且热泵热量传递系数自相关性很强，距离预测时刻越近的时间序列温度数据相关性越强。水泵2频率、太阳辐照度、环境温度与其相关性依次减弱，环境湿度、风速相关性最弱故不予考虑。因此，本文选取组件预测时刻前两个时刻历史数据和水泵2频率、太阳辐照度、环境温度等数据作为神经网络模型的输入参数，预测流程如图2所示。

图2 热泵热量传递系数预测流程图

3.2 Elman神经网络模型

Elman网络是一种典型的递归神经网络，其在某时刻k的输出状态不仅与k时刻的输入状态有关，而且还与k时刻以前的递归信号有关，表现出善于进行动态建模的特性。图3为Elman神经网络结构示意图，包含输入层、隐含层、输出层以及具备动态记忆功能的承接层。

图3 Elman神经网络结构

由前述分析可知，某一时刻热泵热量传递系数与上两时刻的传递系数以及气象数据有较强的相关性。为了提高预测精度本文选择Elman神经网络对热泵热量传递系数进行动态建模。Elman神经网络的数学模型为

x(k)=f(ω1xc(k)+ω2u(k-1))

(2)

xc(k)=x(k-1)

(3)

yk=ω3x(k)

(4)

其中，f(x)取为sigmoid函数，即

(5)

3.3 预测实例分析

3.3.1 数据样本选取与标准化

本文选取2018年7月1日至2018年10月1日晴天、多云天气下的热泵热量传递系数数据作为数据源。选取数据源中2018年7月1日至2018年9月15日热泵热量传递系数数据作为网络训练数据，共500个样本，建立预测模型，选取2018年9月16日至2018年10月1日热泵热量传递系数数据用于检验网络的预测精度，共100个样本。

由于辐照度、温度、湿度、风速等数据量纲不同且大小差异较大，因此对一组数据x={x1、x2…xn}，进行以下标准化变换

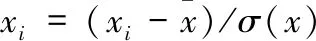
(6)

3.3.2 预测评价标准

本文采用相对误差RE和平均绝对百分误差MAPE对热泵热量传递系数Elman模型预测精度进行评价，两者的计算式分别为：

(7)

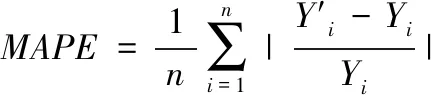
(8)

3.3.3 预测结果

在MATLAB对上述预测系统进行建模之后，本文得出了晴天及多云条件下的Elman神经网络预测结果。图4、图5分别是晴天、多云条件下Elman神经网络模型的热泵热量传递系数预测值与真实值。图6是两种天气条件下，Elman神经网络模型的相对误差。表3为两种天气条件下Elman模型预测误差的评价指标。

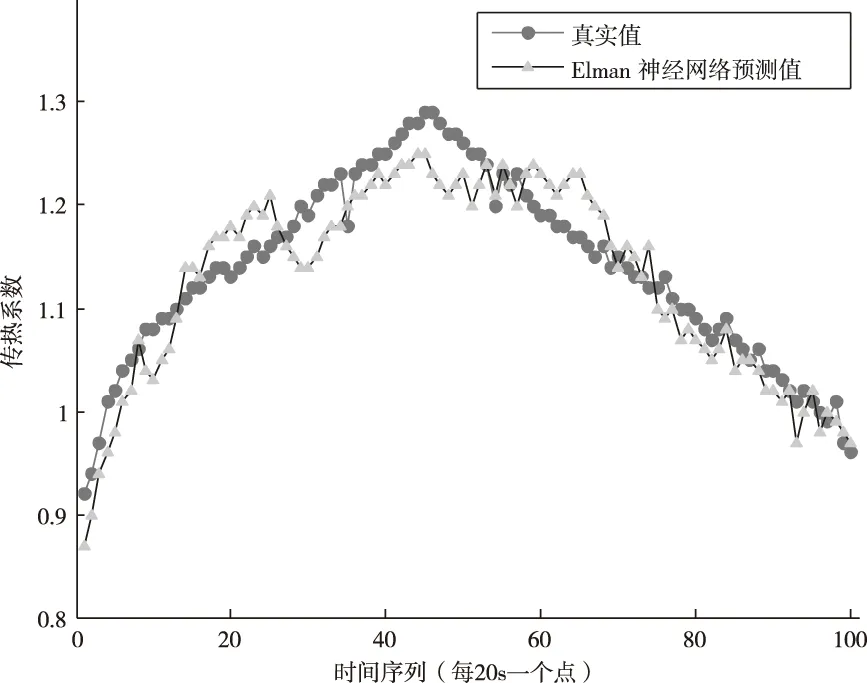
图4 晴天条件下Elman模型预测结果

图5 多云条件下Elman模型预测结果

图6 晴天及多云条件下预测结果的相对误差

表3 Elman模型预测误差评价指标

由图4、图5可知，Elman神经网络模型预测结果符合天气变化情况。由图6、表3可知晴天及多云条件下预测结果相对误差均不超过8%。上述试验结果说明ELman神经网络预测热泵热量传递系数K是可行的，代K值简化热泵部分而得到的PV/T-SAHP系统模型可靠性则尚有待验证。

4 PV/T-SAHP系统模型建立

水冷式PV/T-SAHP系统在运行时属于典型的非稳态导热问题，其可归结为由包含非稳态项的导热微分方程及相应单值性条件所构成的定解问题。完全从分析解的角度求解这类问题难度是很大的。本文选用集总参数法对其作近似动态特性分析。

集总参数法以热能守恒定律为基础，建立物体两端热容量与由不同热传递机制引起的热流之间的平衡方程。

(9)

式中，C——热容量(J/℃)，ρ——密度(g/cm3)；A——(面积)，m2；L——厚度(m)；c——比热容，[J/(kg·℃)]；qcon——传导热流(W/m2)，qcov——对流热流(W/m2)，qra——辐射热流(W/m2)。

4.1 PV/T组件

图7为PV/T组件纵向结构示意图，从上到下依次为玻璃盖板层、光伏电池层、太阳能电池背膜(TPT)层、铝箔纸层、铜管层。

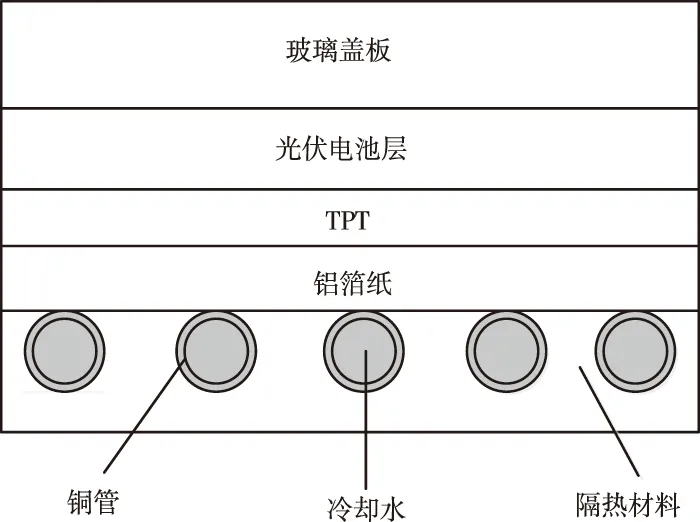
图7 PV/T组件纵向结构示意图

利用集总参数法建立各层热量平衡方程如下：

玻璃层

(10)

式中，G——外来投射辐射(W/m2)；α——辐射吸收比，无量纲，本文中玻璃层及光伏电池层对太阳辐射的吸收比αfg、αpv分别取0.5、0.9。θ——热阻。热阻计算方法为

(11)

光伏电池层

(12)

式中，τfg——玻璃层对太阳短波辐射的透过率，取0.85。

TPT层

(13)

铝箔纸层

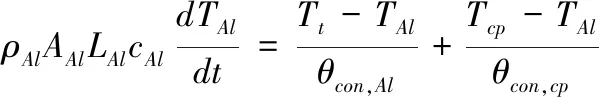
(14)

铜管层

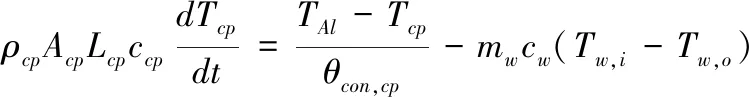
(15)

式中，mw——单个采样周期内流过铜管的水的质量流量；Tw，i，Tw，o分别是集热水箱光伏板侧的进出口水温。

4.2 集热水箱

如图1所示，忽略箱体与环境的热量交换，集热水箱内水温主要受从PV/T组件吸收回来的热量以及由热泵运行蒸发器处所带走的热量影响。

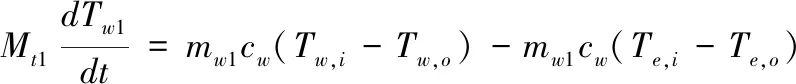
(16)

式中，Mt1是集热水箱中水的总质量，取100kg；mw1——单个采样周期内流过蒸发器的水的质量流量；Te，i，Te，o分别是蒸发器的进出口水温。

4.3 蓄热水箱

蓄热水箱同样忽略其与环境的热量交换，其热量来源只有从热泵冷凝器处吸收。这一部分热量可由式(16)中蒸发器吸收热量量与热泵热量传递系数K共同表示，故蓄热水箱的热量平衡方程为

(17)

式中，Mt2是蓄热水箱中水的总质量，取150kg。

5 V/T-SAHP系统模型验证

5.1 试验数据选取与处理

PV/T-SAHP系统模型由式(10)～(17)的常微分方程组构成，光伏板温度是其中一个可求量，且本文中光伏板温度可通过温度传感器测得，故选择其作为模型验证变量。

本文根据天气预报选择2018年8月13日、8月27日分别作为晴天天气、多云天气的实验日，PV/T-SAHP系统全天运行，早上10点左右，开启热泵，经过10分钟通水降温光伏板温度显著降低且逐渐趋于稳定。数据采集系统每隔20s时间采集一次数据并存入数据库。本文选取上述两典型天气日数据代入PV/T-SAHP系统模型，验证其准确性。同样，用式(6)对数据进行标准化处理。

5.2 预测评价标准与结果

PV/T-SAHP系统数学模型预测精度仍采用相对误差RE和平均绝对百分误差MAPE进行评价。

在Simulink软件中搭建前述数学模型，并将各项已知参数如ρ、A、L、c、k等[11]以及由数据采集系统采集的环境温度Thj、太阳辐照度Gr和风速Ws输入，可求出PV/T组件各层结构以及集热水箱、蓄热水箱的温度值，之后不断进行迭代可得温度动态变化情况。

图8、图9分别为晴天及多云条件下数学模型的光伏板温度预测值及真实值。图10为晴天及多云条件下，预测结果的相对误差值。表4为两种天气条件下数学模型预测误差的各项评价指标。

图8 晴天条件下的数学模型预测结果

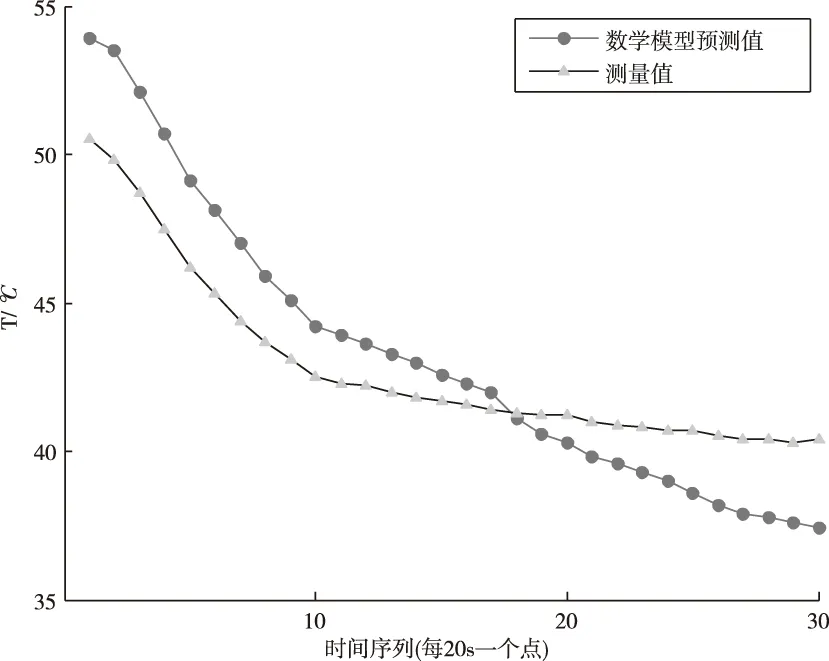
图9 多云条件下的数学模型预测结果

图10 两种天气条件下，预测结果的相对误差

表4 预测误差评价指标

由图8～9可知，在晴天及多云条件下，数学模型预测值与真实值的走势相近。由图10及表4可知，数学模型预测值的相对误差均在10%以内，基于集总参数法的PV/T-SAHP系统动态模型仿真性能较好。

6 结论

本文以光伏光热一体化热泵系统为研究对象，提出一套更为简单的系统建模方案，并利用实验平台验证了该方案的可行性，具体结论如下：

1)从热泵蒸发器侧传递到冷凝器侧的热量可以用神经网络算法进行预测，从而避免复杂耗时的数学计算。实验结果表明，Elman神经网络预测模型对热泵热量传递系数预测精度较高，相对误差集中在1%～6%之间。

2)在Elman神经网络预测模型的基础上，基于集总参数法建立的PV/T-SAHP系统动态模型的能较好模拟系统实际运行情况。