低速无人驾驶纵向运动控制的仿真研究
2021-12-10曹志雄
唐 坤,曹志雄
(北京天隼图像技术有限公司,北京 100000)
1 引言
低速无人驾驶相较于高速无人驾驶,其技术特点有:首先,由于低速无人驾驶车辆(后文低速无人车均指此类低速无人驾驶车辆)的行驶速度远小于高速无人驾驶车辆,因此二者在控制周期、测量精度以及逻辑决策等方面都有较大差异;其次,低速车辆多应用厂区、景区等特定的环境,这些场地通常为非规范化的道路或缺乏明显的道路标识,突发状况较多,因此,要求其能够对控制命令有快速、准确的响应;再次,低速车辆的线控底盘多为自主研发,没有统一的制式标准,给控制增添了许多不确定因素[1]。
目前,国内外已有一些研究机构对于车辆纵向控制进行了各种尝试。如基于PID控制的优化算法,卡内基梅隆大学研究团队采用非线性PID控制策略[2];国内百度团队的“阿波龙”采用的位置-速度双闭环PID控制。再如基于滑模控制的算法,意大利的帕维亚大学研究团队提出了纵向二阶滑模控制策略;以及韩国的Liang H等人提出的参数滑模下位控制策略[3,4]。如基于模糊控制的算法,法国的P.F.Toulotte等提出的具有极点配置功能的模糊纵向控制策略[5]。还有清华大学宾洋团队提出的非线性干扰解耦和变结构控制原理的鲁棒控制算法[6]。以及日本东京大学的M.Omae等人提出的基于鲁棒控制理论的前馈加H-infinity反馈的纵向控制策略[7]等。
本文通过对上述纵向运动控制算法的研究总结,并结合低速无人车工作环境和自身结构的特点,对低速无人驾驶纵向运动控制进行了仿真研究。
2 低速车试验平台介绍
低速无人车的底盘多为自主研发,因此,在建立仿真平台时,无法采用通用底盘模型。本文以北京天隼图像技术有限公司研发的FELIS AHC201型线控底盘为基础进行了仿真平台的搭建。其中FELIS AHC201是一款针对园区物流/移动充电等商业应用而研发的小尺寸、载重型线控底盘,其结构如图1。

图1 FELIS AHC201结构
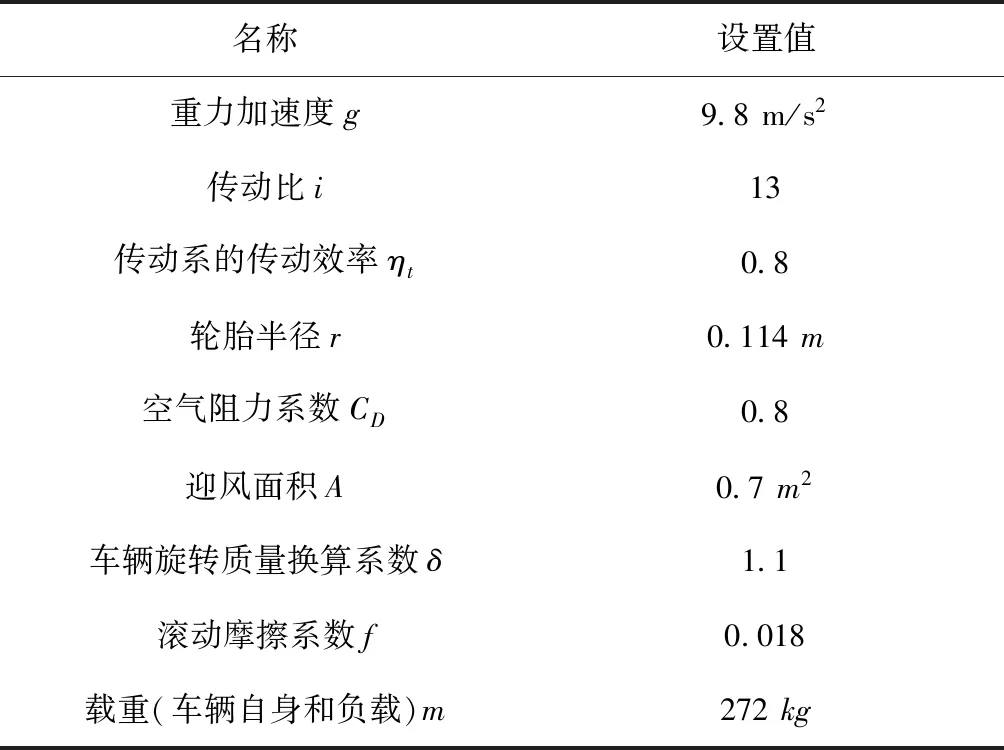
FELIS AHC201主要集成了主控系统、双横臂独立悬架系统、阿克曼转向系统、电磁驻车制动系统、液压行车制动系统以及后桥差速驱动系统,配备了高精度转角传感器、内置电机编码器,其车辆参数配置见表1。

表1 FELIS AHC201整车参数
其中驱动系统主要包括驱动电机、电机控制器、差速器等,根据驱动控制指令,控制驱动电机输出驱动转矩;行车制动系统采用电子液压制动技术,根据制动控制指令,控制行车制动总成输出作用于车轮的制动压强。
3 Carsim/Simulink联合仿真平台建立
3.1 Carsim车辆模型与接口设置
基于FELIS AHC201完成了Carsim车体参数、各个机械系统(转向系统、悬架以及轮胎等)参数以及控制方式的设置。
目前Carsim尚未开发针对电动车辆的仿真模块,因此,将驱动系统设置为由Carsim外部直接提供作用于差速器的驱动转矩,如图2。
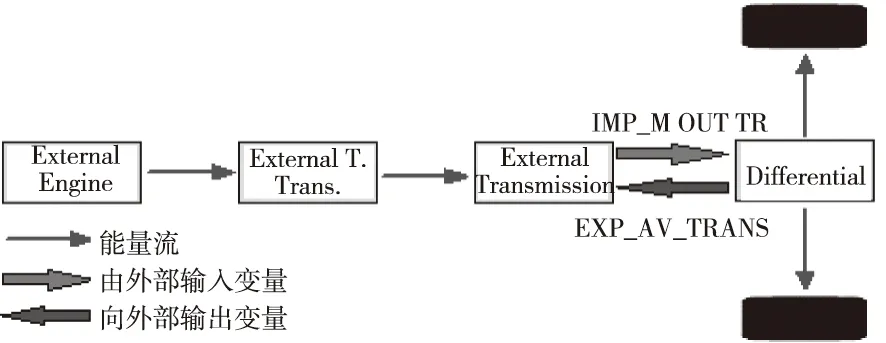
图2 Carsim车辆模型的动力系统
制动系统设置为由Carsim外部直接提供作用于轮胎的制动压强。而驱动系统和制动系统的数学模型[8,9]则根据电机驱动特性以及制动系统的动力学关系在Simulink中搭建。
Carsim与Simulink联合仿真的实现,需要对二者之间的输入输出接口进行设置,基于纵向速度控制的输入输出数据设置见表2[10]。
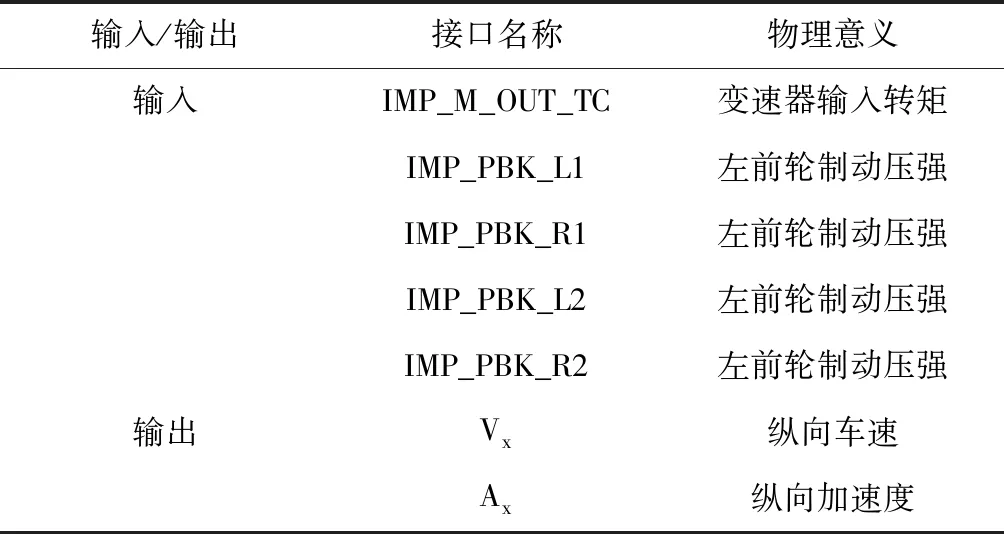
表2 Carsim/Simulink联合仿真输入输出接口设置
3.2 驱动电机模型
驱动系统的输出特性需要满足车辆动态性能指标要求,如加速、爬坡性能等。在驱动过程中,驱动电机与传统发动机的区别在于驱动电机具有一定的过载能力,根据发动机驱动特性的原理,采用电动机的峰值特性进行动力性能分析[11]。假设驱动电机具有理想的峰值特性,其峰值转矩-转速关系曲线如图3。
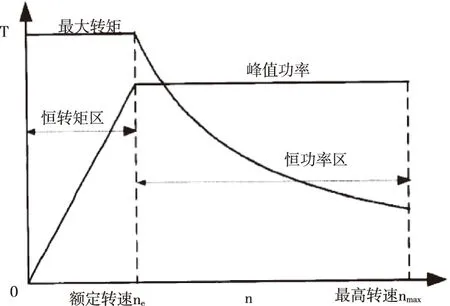
图3 驱动电机峰值特性曲线
实际电机控制器的加速信号为0~5V信号,经过标定转换,转换为转矩占空比Lac,在给定转速n下,驱动电机输出转矩的表达式为

(1)
式中,ne为电机基速;Tn_max为在给定转速n下,电机的峰值转矩;Pn_max为在给定转速n下,电机的峰值功率[12]。
综上,根据式(1)中转矩占空比Lac、转速n和输出转矩Te的函数关系,结合电机参数,见表3。
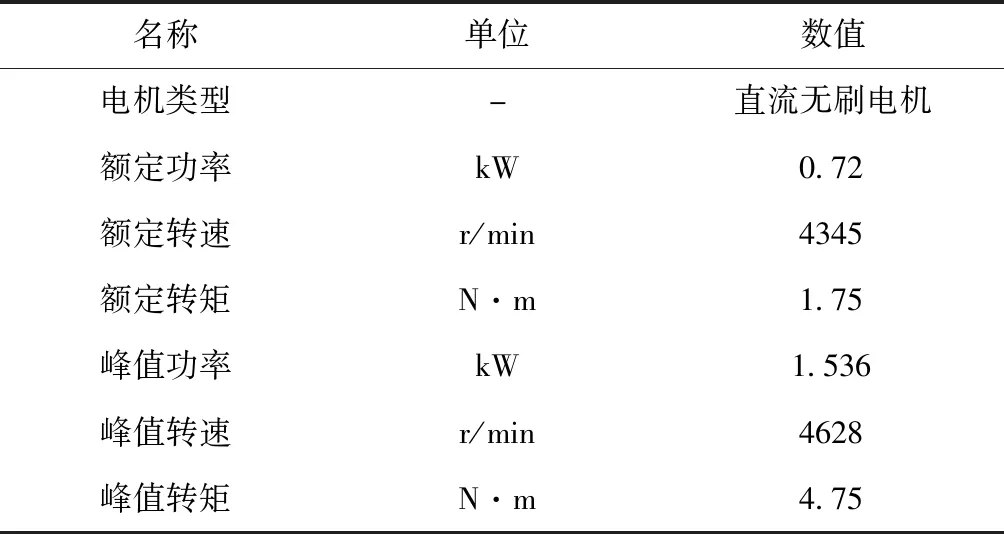
表3 FELIS AHC201驱动电机参数
利用MATLAB建立关于电机特性的MAP图作为电机模型,以转矩占空比Lac、转速n作为输入,输出转矩Te作为输出。如图4。
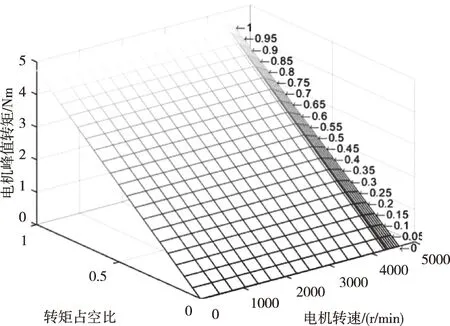
图4 电机峰值特性MAP图
3.3 制动系统模型
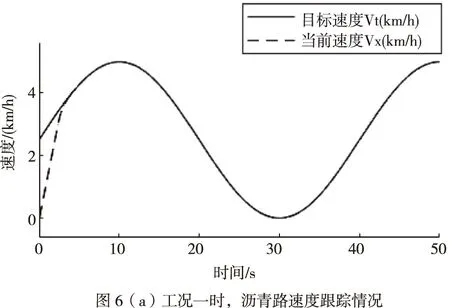
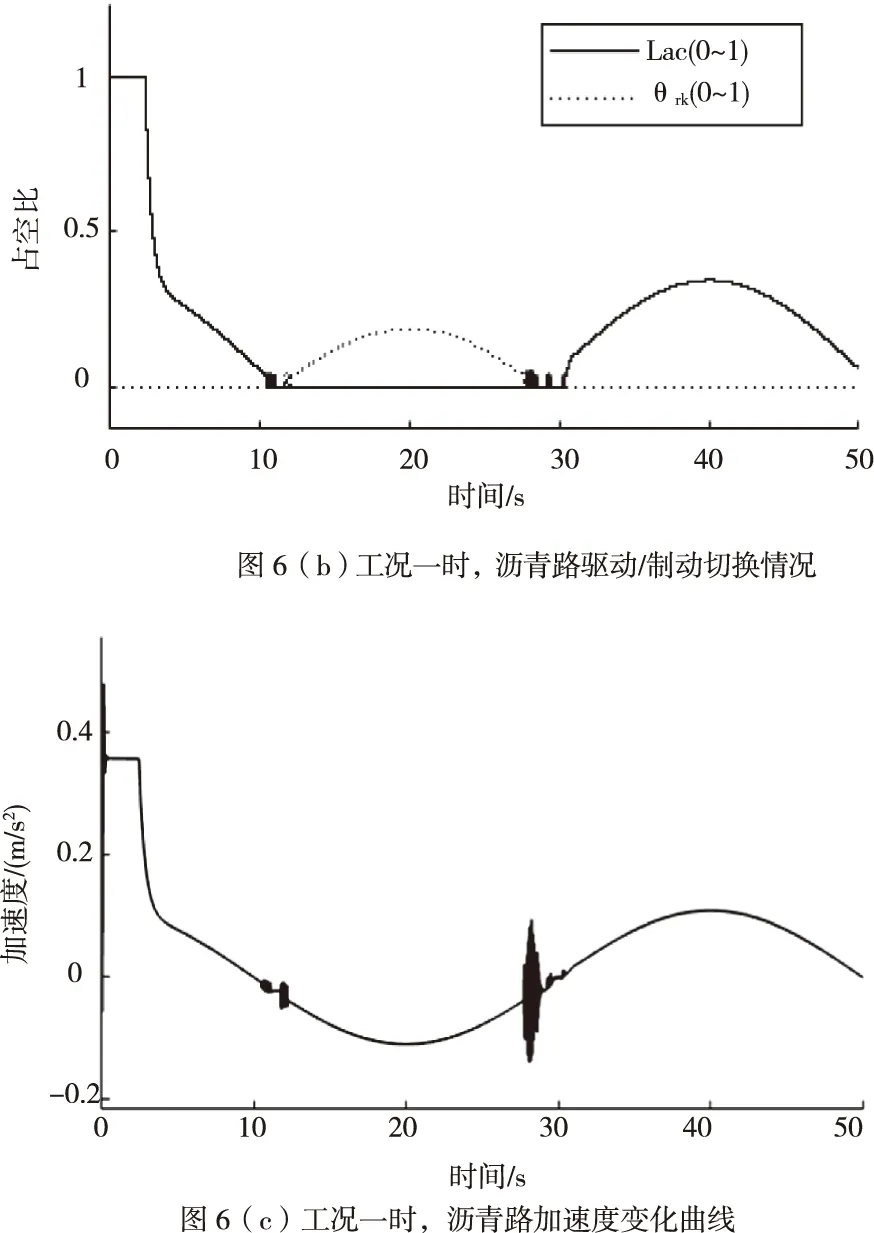
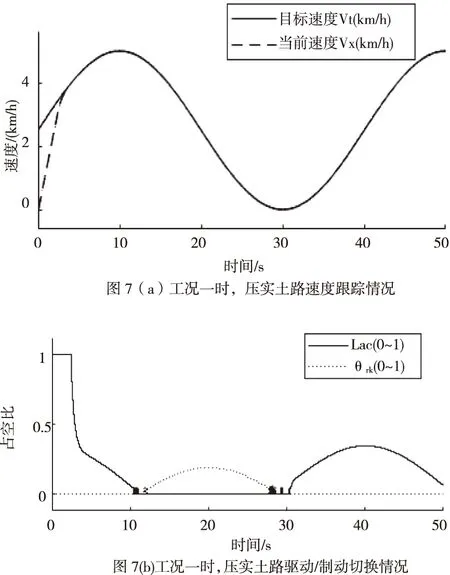
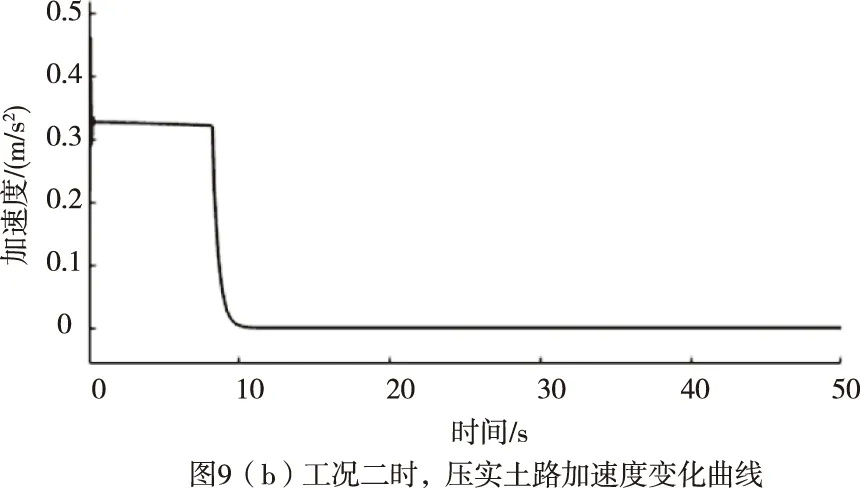
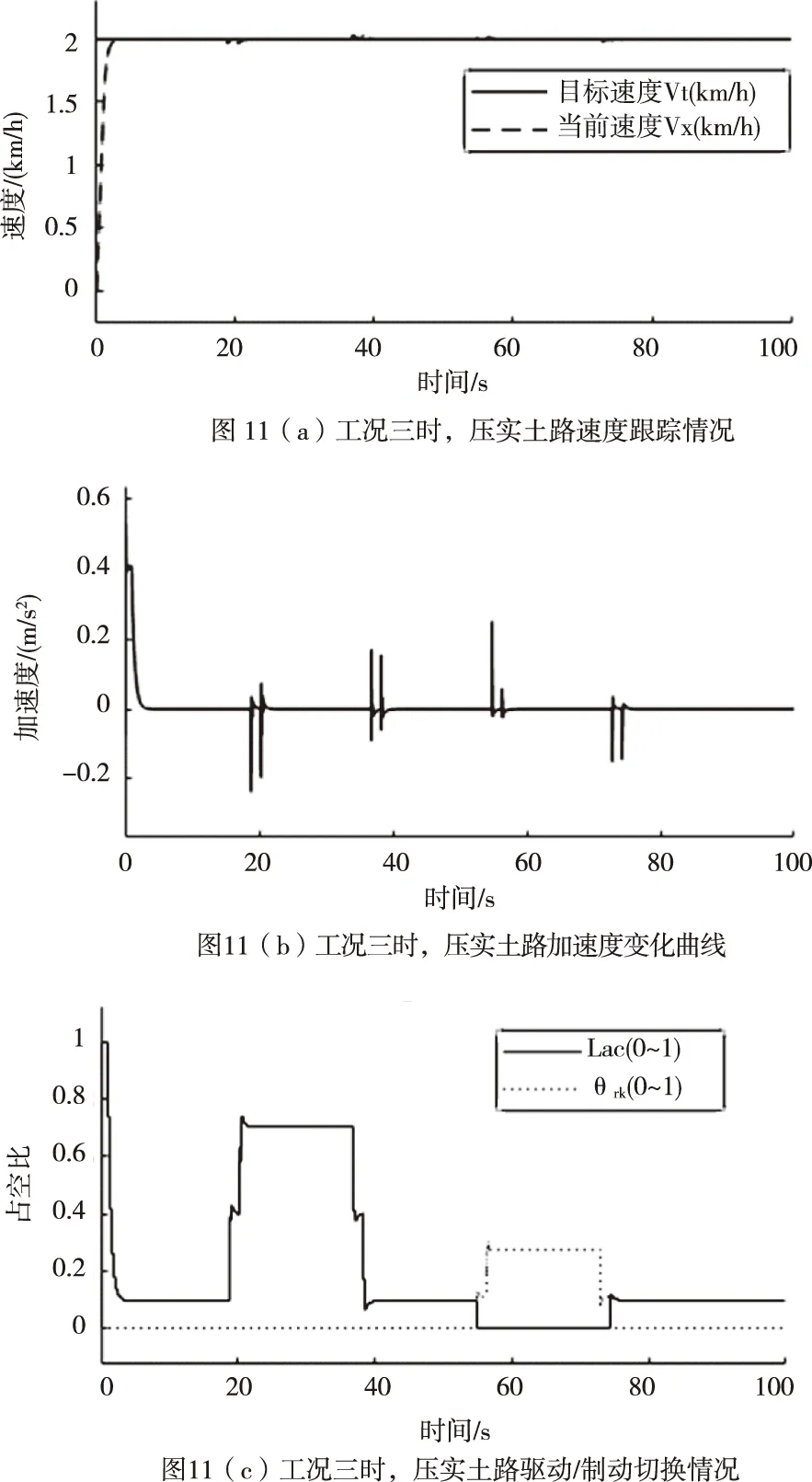
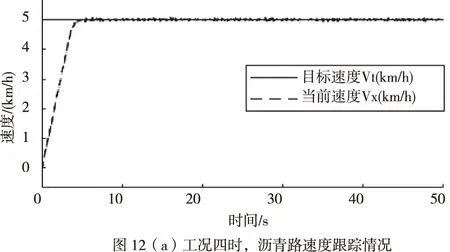
车辆在行车制动时,车轮制动动力源由电子液压制动总成提供,同样将其控制器0~5V制动信号标定转换为制动占空比θrk,通过实车测试拟定出车辆加速度a与θrk的函数关系:a=fBrk(θrk);根据车辆动力学平衡,可以确定加速度a与制动力Frk的函数关系:Frk=fa(a)。因此,在Frk Frk=k1·θrk+k2 (2) 式中: 制动力Frk又与作用于车轮的制动压强Pdes(MPa)呈线性关系:Pdes=kFrk,其中k=1.21,由此求得车轮制动压强Pdes。 控制器的功能为通过一定的控制策略调节车辆的纵向速度(Vc),使其能够稳定、准确、快速的对目标速度(Vt)进行跟踪。控制器整体结构设计为分层式,如图5。 图5 控制器结构框架 其中上位机控制器通过PID+LQR补偿控制算法计算期望加速度ades。下位机控制器通过切换逻辑判断需要执行的控制(驱动/制动控制),然后根据车辆的逆动力学模型,求取驱动占空比Lac或制动占空比θrk。 上位机控制器采用PID+LQR自适应补偿控制算法。PID控制采用增量式PID的方式,以目标速度与当前速度的偏差e作为输入,控制产生加速度apid。 理想条件下,期望加速度与输出加速度成一阶惯性的关系[13]: (3) 但在实际中,由于车辆系统强非线性、外界扰动等原因,实际输出的加速度as与理想的输出加速度a存在一定的偏差,因此,需要一定的补偿控制来纠正偏差,即 (4) 式中:△an补偿的加速度;as为补偿后实际输出加速度,此时,as=a。 利用前向欧拉法,将上式(4)离散化,得到状态空间方程: X(k+1)=AX(k)+B1W(k)+B2U(k) Y(k+1)=CX(k) (5) 由于控制系统的控制目标为控制车辆的速度,因此将车速作为系统的输出,即C=[1 0]。 设实际状态变量X想状态变量Xd偏差为E,则有 E(k+1)=AE(k)+B1W(k)+B2(U(k)-Ud(k)) (6) 式中,以目标车速的实时状态作为理想状态,E(k)=X(k)-Xd(k)为k时刻的状态偏差,由于U(k)=Ud(k),因此, E(k+1)=AE(k)+B1W(k) (7) 这样,将系统误差问题转化为状态调节问题,根据LQR寻优控制的原理,针对式(7)对应的系统,设置目标函数为 (8) 式中,Q和R分别为E和W对应的权重矩阵,并对目标函数进行离散化处理。 设置式(7)对应系统的反馈控制器为 W(k)=-G·E(k) (9) 式中,G为状态反馈增益矩阵。 将式(9)代入式(8),求解其对应的Riccati方程,获取G,进而获得补偿加速度△an。 因此,可求得补偿后上位机控制器输出的期望加速度ades为 ades=apid+△an (10) 下位机控制器的任务包含:逻辑切换、通过驱动或制动的逆动力学模型计算驱动控制占空比Lac或制动控制占空比θrk。 在切换逻辑中,根据期望加速度ades的正负方向,决定施加何种控制。当ades>0时,表示车辆正在加速,施加驱动控制;当ades<0时,表示车辆正在减速,施加制动控制。但为了防止驱动与制动频繁切换,设置一定的缓冲区间[-0.1,0.1],在缓冲区间内,不施加任何控制,即Lac=0和θrk=0。综上,其切换逻辑设计为 (11) 根据加速过程车辆动力学平衡,逆向推导出电机驱动力矩Ttq与车辆加速度a的关系: (12) 式中,ua为车辆行驶速度(km/h)。由此,根据期望加速度ades,能够计算得到期望的驱动力矩Tdes,涉及参数见表4。 表4 FELIS AHC201动力系统相关参数 根据驱动电机的输出转矩的能力,设置标定转矩:Tref=4.75Nm,由此确定转矩占空比: (13) 同理,根据制动过程车辆动力学平衡,逆向推导出制动压强Pμ与车辆加速度a的关系: (14) 由此,根据期望加速度ades,能够计算得到期望的制动压强Pdes,涉及参数见表5。 表5 FELIS AHC201制动系统相关参数 根据制动总成提供制动压强能力,设置其标定压强:Pref=10MPa,由此确定制动占空比 (15) 通过Matlab/Simulink和Carsim联合仿真平台,对基于上述控制器的纵向速度跟踪控制系统的控制性能进行仿真测试。参照FELIS AHC201的性能指标,设计仿真工况,对比仿真结果,确定控制性能,FELIS AHC201的性能指标见表6。 表6 FELIS-AHC201的性能指标 仿真分别在Carsim 模拟的沥青路和压实土路环境中进行,控制周期设置为0.01 s,根据FELIS AHC201的性能指标,设置沥青路的最高行驶车速为13 km/h,压实土路的最高行驶车速为10 km/h,设置多种工况,分别测试速度跟踪控制性能、加速控制性能、爬坡控制性能以及抗干扰的能力。 1)工况一:在两种路面环境下,设置目标车速成正弦周期变化,周期为40 s,幅值为2.5 km/h。 2)工况二:在两种路面环境下,设置目标速度保持最高车速行驶。 3)工况三:在两种路面环境下,依据根据FELIS AHC201性能指标,设置目标速度保持最低爬坡速度2 km/h行驶。车辆在平直路面行驶10 m,突遇坡度为20%的上坡道路,行驶10 m后,上坡结束;继续平直行驶10 m后,遇到坡度为20%的下坡道路行驶10 m后,下坡结束;继续平直行驶10 m。 4)工况四:在两种路面环境下,设置目标速度保持为5 km/h,外部环境设置(4~5)m/s风速的干扰。 1)按照工况一的设置,当车辆行驶在沥青路时,在行驶4.4 s后,实现了对目标车速的有效跟踪,最大超调量为0.2 km/h,延滞时间为0.1 s,如图6(a);驱动与制动的占空比信号能够有效、及时的实现切换,如图6(b);运行至30 s附近时,目标车速近似为0 m/s,并且其变化缓慢,造成驱动与制动切换频繁,加速度波动较为剧烈,其最大波动值为0.16 m/s2,远小于性能指标的要求值0.5 m/s2,如图6(c)。当车辆行驶在压实土路时,在行驶4.6 s后,实现了对目标车速的有效跟踪,最大超调量为0.1 km/h,延滞时间为0.1 s,如图7(a);驱动与制动的占空比信号能够有效、及时的实现切换,如图7(b);驱动与制动切换造成加速度产生的最大波动值为0.13 m/s2,同样小于性能指标的要求值0.5 m/s2,如图7(c)。 2)按照工况二的设置,当车辆行驶在沥青路时,设置目标车速为最高车速13 km/h,最大超调量为0.2 km/h,车速上升时间为8.5 s,小于性能指标的要求值10 s,如图8(a);加速度的最大值为0.49 m/s2,小于性能指标的要求值0.5 m/s2,如图8(b)。当车辆行驶在压实土路时,设置目标车速为最高车速10 km/h,最大超调量为0.1 km/h,车速上升时间为6.2 s,小于性能指标的要求值10 s,如图9(a);加速度的最大值为0.46 m/s2,同样小于性能指标的要求值0.5 m/s2,如图9(b)。 3)按照工况三的设置,当车辆行驶在沥青路和压实土路两种环境时,每一次路况的变化引起速度波动后,都能及时有效的恢复速度的跟踪,最长恢复时间均小于4 s,保持了对低爬坡速度的跟踪,速度偏差的范围在[-0.1,0.1] km/h之间,如图10(a)和11(a);加速度的波动范围在[-0.2,0.4] m/s2之间,满足性能指标要求的[-0.5,0.5] m/s2,如图10(b)和11(b);驱动与制动能够实现及时有效的切换,如图10(c)和11(c)。 4)按照工况四的设置,当车辆行驶在沥青路和压实土路两种路面环境时,外部风速干扰使得车速产生了一定的波动,速度偏差的范围控制在[-0.2,0.3] km/h之间,如图12(a)和13(a);相应加速度的波动范围为[-0.4,0.5] m/s2,满足性能指标要求的[-0.5,0.5] m/s2,如图12(b)和13(b)。 综上仿真测试,其测试结果表明: 1)控制系统具有良好跟踪控制能力。工况一的测试中,两种路面环境速度跟踪的延滞时间、超调量以及上升时间均满足控制系统的设计要求,加速度变化范围满足性能指标的要求,加速与制动实现平稳切换,跟踪过程平稳。 2)控制系统具有良好加速控制能力。工况二的测试中,两种路面环境的最高车速的加速时间均小于性能指标要求值,并且加速过程速度上升平稳,加速度的最大值均小于性能指标的要求值。 3)控制系统具有良好的爬坡控制能力。工况三的测试中,两种路面环境下,控制系统均能够实现性能指标要求的最大爬坡度;并且每一次路况转换,均实现了对目标车速的快速、准确的跟踪。 4)控制系统具有良好的抗干扰能力。工况四的测试中,能够克服外部风速干扰,保持了对目标车速的准确、平稳的跟踪。 本文基于FELIS AHC201型线控底盘的结构及参数,搭建了车辆纵向运动控制系统的联合仿真平台。针对低速无人车的纵向速度跟踪控制的需求,设计了基于分层结构及PID+LQR补偿控制算法的速度跟踪控制器。并对纵向速度跟踪控制系统的控制性能进行了仿真测试,仿真结果表明在不同工况条件下,该系统满足车辆性能指标的要求,实现了预期的设计目标。 后续针对低速无人车运动控制将要开展的工作:首先通过实车测试,优化Carsim车辆模型参数,完善联合仿真平台;其次设计、优化运动控制策略,完善运动控制系统;最后利用仿真测试平台,逐步代替实车测试平台,开展车辆运动控制系统相关性能的测试,以此来缩短运动控制系统的开发周期,降低测试风险。4 控制器的设计
4.1 控制器结构

4.2 上位机控制器设计
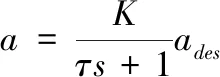

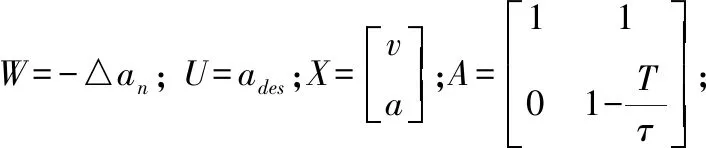
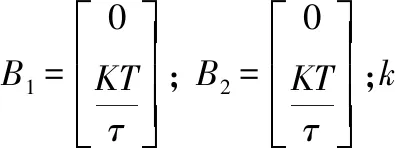

4.3 下位机控制器
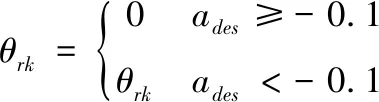
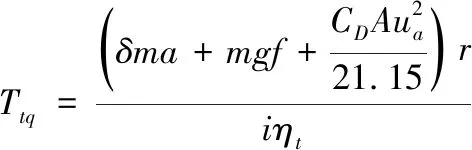
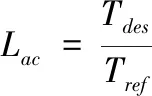


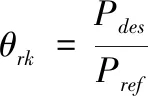
5 仿真测试

5.1 仿真设计
5.2 仿真结果






6 结论
