基于SelQPSO的WMR区间二型模糊逻辑控制
2021-12-10结昆仑佃松宜
结昆仑,赵 涛,佃松宜
(四川大学电气工程学院,成都 610065)
1 引言
轮式移动机器人(WMR),可在危险恶劣人工难以到达的地方移动,其在航空航天、工业、商业、核电、石油工业、船舶行业等领域得到广泛使用[1,2,3]。而环境结构复杂、环境恶劣等因素导致人工操作十分困难,所以对于WMR的控制成为关键研究技术之一。
WMR是一种特殊的非线性系统[4],其跟踪的期望轨迹随着时间的变化而变化,这导致WMR的轨迹跟踪控制成为难题,而模糊逻辑控制(FLC)在处理这类非线性问题方面体现出较好的性能。文献[5]通过FLC动态调节快速双幂次趋近律参数,从而减小滑模控制造成的抖振现象。文献[6]采用Back-stepping建立机器人运动学控制器,滑模控制建立机器人动力学,通过FLC调节滑模增益,以减小控制过程中出现的抖振现象。文献[7]通过GT2FLC调节非奇异终端滑模控制器的趋近律增益,以提高系统响应速度,文献[8]通过粒子群优化算法对交叉算子进行了优化,提高了对WMR控制的收敛速度和稳定性。然而,以上控制方法需要建立精确的数学模型,很少考虑外部干扰的情况,FLC的隶属函数参数大多数是通过专家经验选择。
模糊逻辑控制(T1FLC)是由Zadeh[9]教授通过对人脑研究于1965年提出的一种智能控制。之后已成功运用在移动机器人控制[10]、模式识别、管理决策等领域。针对T1FLC对被控对象模糊化程度低、受不确定性因素影响大的问题,Zadeh教授于1975年提出了一种二型模糊逻辑控制[11](T2FLC),T2FLC描述事物更加全面,但随之而来的是计算量增大,之后人们为了简化计算量,将T2FLC中的次隶属度均设为1,即区间二型模糊(IT2FLC)。
在IT2FLC中,其核心是模糊控制规则的建立[12],而模糊控制规则的建立是通过设置相应的隶属函数参数,设置隶属函数参数常用的传统方法包括基于专家经验与控制工程知识、基于操作人员操作经验、基于过程的模糊模型等,而这些方法容易造成不必要的误差,导致控制精度降低。
粒子群优化算法(PSO)是由Kennedy与Eberhart通过对鸟群研究于1995年提出的一种优化算法[13]。由于PSO是通过模拟鸟群设计的,其随机性和群体智能性不高,之后J.Sun等[14]人将普通粒子替换成具有量子行为的粒子,提出了QPSO算法,提高了PSO全局收敛性能。针对QPSO算法,文献[15]通过将自然选择机理与量子行为粒子群优化算法结合的方式,进一步对QPSO进行改进,以提高算法全局收敛性和求解精度。本文将采用改进的QPSO算法对IT2FLC的隶属函数参数进行优化。
本文所做的贡献主要有:①根据WMR数学模型,针对轨迹跟踪控制问题,设计了基于优化思想的IT2FLC,来实现WMR轨迹跟踪控制;②针对IT2FLC中隶属函数参数难以确定问题,通过改进的QPSO算法(SelQPSO)对隶属参数进行优化,从而提高IT2FLC控制精度;③通过增加外部扰动验证了本文所提的控制方法具有较强的抑制扰动能力。最后通过仿真验证了本文所提的控制方法与经过QPSO优化的IT2FLC、未经优化的IT2FLC以及T1FLC算法相比具有更好的性能。
2 轮式移动机器人
2.1 WMR数学模型
WMR在一个平面工作时,需要通过控制每个车轮转速,间接控制其整体线速度、角速度从而能精确地跟踪上一条给定轨迹,到达期望位置,WMR结构示意如图1。
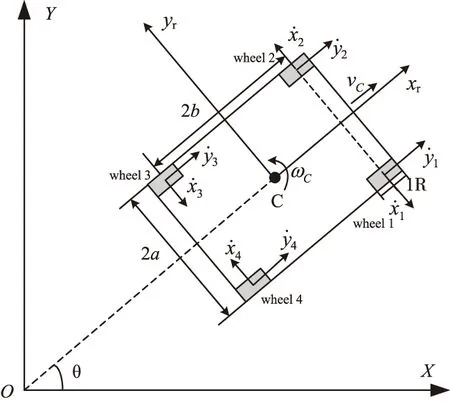
图1 WMR结构示意图
其中,C为WMR质心,R为磁轮半径,2a为WMR宽度,2b为WMR两车轮中心的距离,vC为WMR整体线速度,ωC为WMR整体角速度,θ为WMR运动方向与X轴夹角,即为WMR的姿态角。
注1:WMR的质心与其几何中心吻合,且线速度
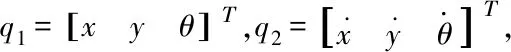

(1)
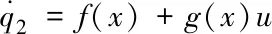
(2)
其中
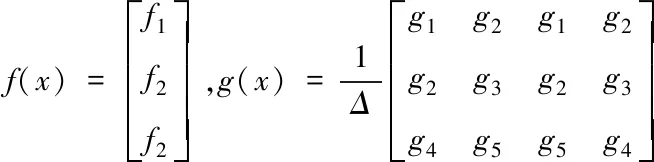
(3)
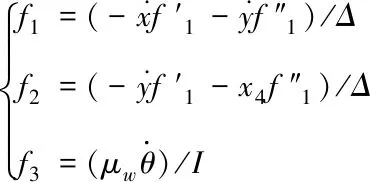
(4)
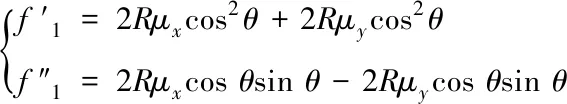
(5)
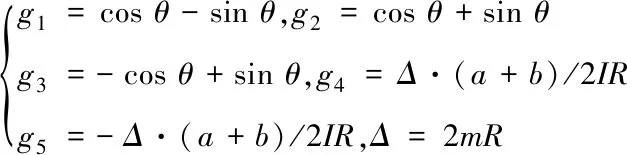
(6)
μx,μy,μw分别为WMR横向移动、纵向移动、原地移动时车轮与平面间的摩擦系数,m为WMR质量,I为WMR的转动惯量,u为车轮的转矩矩阵。
2.2 WMR误差模型


(7)
其中,vCr为WMR整体参考线速度,ωCr为WMR整体参考角速度,
本文设计的WMR轨迹跟踪控制器,其主要是通过控制输出u间接控制vC、ωC,且vC,ωC有界,使其在任意初始误差情况下,在有限时间内快速跟踪上期望轨迹,即
注2:控制输出u通过系统耦合性间接控制vC、ωC。
3 区间二型模糊逻辑系统
在处理非线性系统控制问题上,传统的T2FLC要优于T1FLC,但是T2FLC内部的计算量十分大,不适用于实际工程,于是人们提出了IT2FLC,相对于T2FLC,IT2FLC是将次隶属度均设置为1的一种特殊T2FLC,T2FLC模糊集A[11]表示为
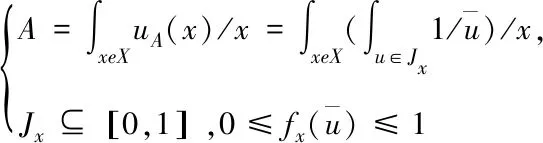
(8)
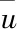
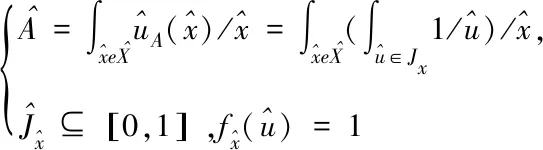
(9)
定义 1[17]:二型模糊集中所有的主隶属度组成的集合称之为A的不确定迹,记为FOU(A),如式(10)所示
FOU(A)=∪xeXJx
(10)
FOU(A)由模糊集上隶属度UMF和下隶属度LMF两条曲线构成,其取值的好坏直接影响IT2FLC的控制效果,如图2,阴影部分为不确定迹。
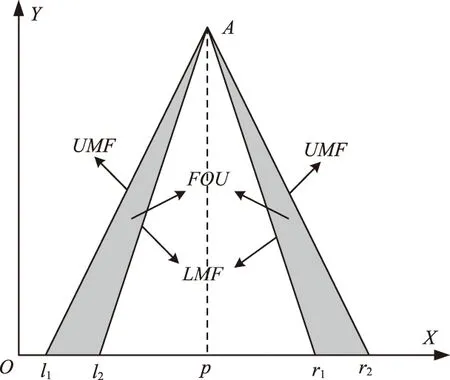
图2 三角形模糊集合的FOU
IT2FLC与T1FLC系统组成十分类似,都包括模糊器、规则库、模糊推理、解模糊等。不同之处是IT2FLC在进行解模糊前,要先进行降型计算,本文所用的降型方法为中心集降型法[18](Center of sets,CS),如式(11)。
(11)
其中,
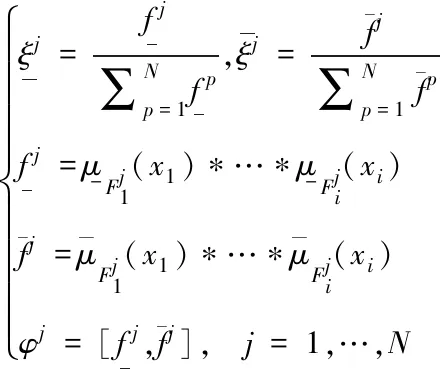
(12)
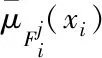
系统输出通常取Ycos(x)的中点,即
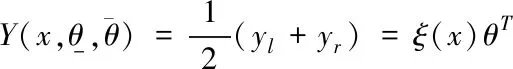
(13)
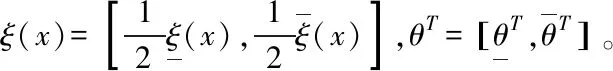
4 改进的量子粒子群算法原理
4.1 量子粒子群算法原理
QPSO算法本质是在一个M维目标空间中[19],假设群体中有N个粒子潜在问题,即
X(t)={X1(t),X2(t),…,XN(t)},在t时刻,第i个粒子位置为X(t)=[Xi,1(t),Xi,2(t),…,Xi,M(t)],其中i=1,2,…N,单个粒子最好位置表示为Pi(t)=[Pi,1(t),Pi,2(t),…,Pi,M(t)],群体最好位置表示为G(t)=[G1(t),G2(t),…,GN(t)],且G(t)=Pg(t),其中下标g表示群体全局中位置最好的粒子,g∈{1,2,…N}。群体中单个粒子最好位置由式(14)确定
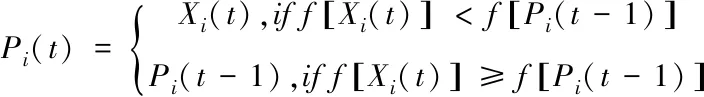
(14)
群体全局最好位置由式(15)确定

(15)
其中,转换搜索空间采用蒙特卡洛模拟法(Monte Carlo Simulation)求解粒子更新方程
Xi,j(t+1)=pi,j(t)±Li,j(t)/2·ln(1/ui,j(t))
(16)
pi,j=φj(t)·Pi,j(t)+[1-φj(t)]·Gj(t)
(17)
其中,φj(t)~U(0,1),ui,j(t)~U(0,1),算法在优化过程中,当Li,j(t)收敛到0时,群体收敛到最好位置,通过平均最好位置优化法控制Li,j(t),即
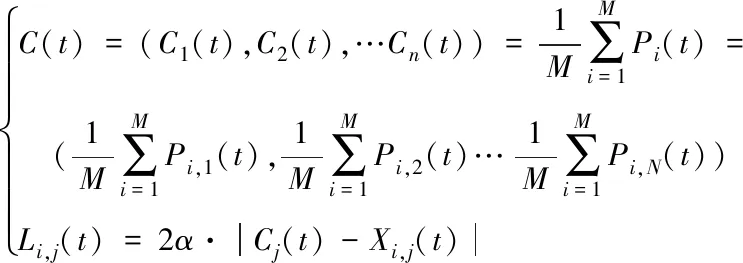
(18)
其中,α为收缩-扩张系数,可采用固定值或线性减小法确定其值大小,一般取α<1.781。
4.2 改进量子粒子群算法原理
SelQPSO是通过自然选择机理将每次迭代后的群体按适应值排序,用最好位置粒子替代最差位置粒子[15]。
SelQPSO算法中粒子数的选择过程由式(19)确定:
(19)
其中,Fitness(X(t))为t时刻粒子适应函数值矢量。粒子位置矢量由式(20)确定:
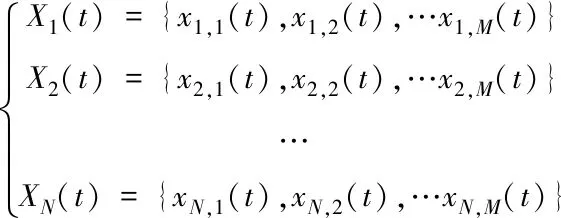
(20)
粒子位置排序通过适应函数对比得到,具体由式(21)确定
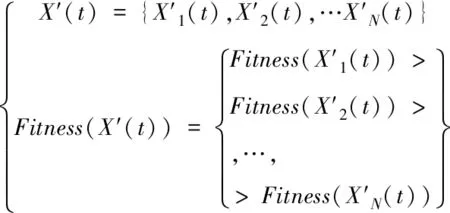
(21)
粒子位置向量改变后进一步进行搜索计算
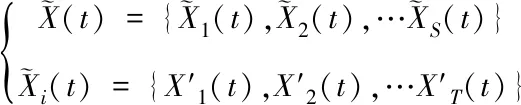
(22)

5 区间二型模糊控制系统设计与优化
5.1 控制系统设计
本节针对WMR系统,将设计有效控制系统,通过控制νC、ωC,使WMR在初始位姿q上,通过有限时间内速跟踪上期望轨迹到达期望位姿qr。其控制优化原理如图3。

图3 WMR模糊控制与优化原理图

定义系统跟踪误差
e=qr-q
(23)
控制器采用if-then规则对WWCR控制量进行调节

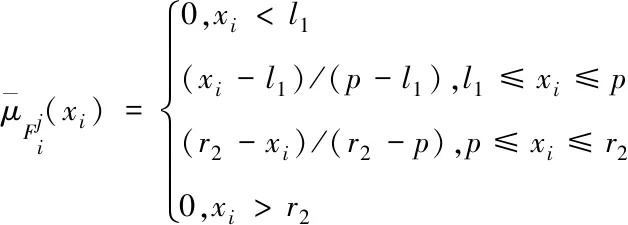
(24)

(25)
其中,p上、下隶属函数的均值,l1,l2,r1,r2分别为上、下隶属度与X轴的交点到原点O的距离,如图3所示,即组成不同的区间。模糊推理采用基于学习的Mamdani型,模糊降型采用CS法,解模糊采用面积重心法(Centroid),模糊规则见表1。
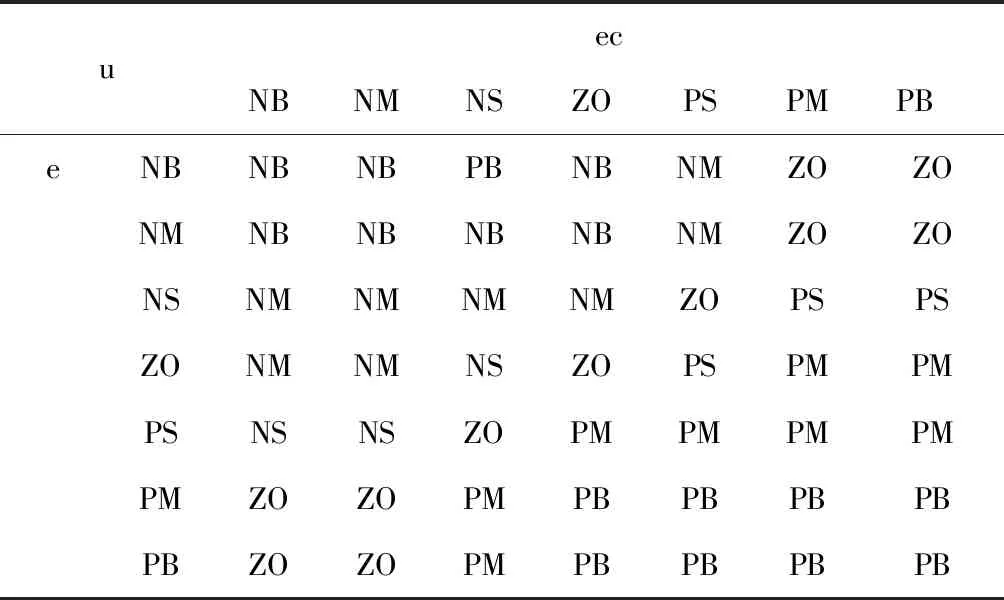
表1 WMR轨迹跟踪控制模糊规则表
5.2 隶属函数模糊规则参数优化
模糊控制效果的好坏取决于模糊控制规则,而传统的模糊规则建立一般采用专家经验、控制工程知识或操作人员实际控制经验等。为提高控制效果与精度,本文通过上一节所介绍的优化算法SelQPSO,对隶属函数参数进行优化,通过自然选择机理将粒子群按适应值排序要比单纯QPSO拥有更好的收敛速度与求解精度,取时间与误差乘积绝对值后的积分作为适应度函数,如式(26)
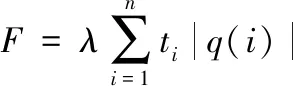
(26)
其中,F为适应函数,λ为计算步长,ti为i时刻,|q(i)|为i时刻误差。SelQPSO算法优化流程如图4。

图4 SelQPSO算法流程图
6 仿真结果与分析
WMR参数及其相应值见表2。
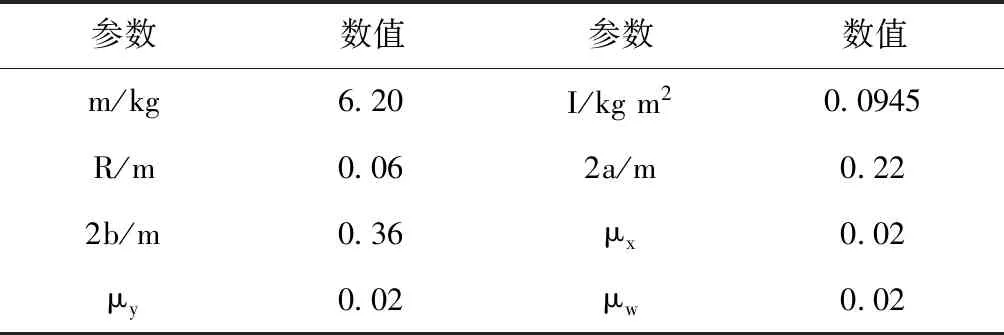
表2 WMR参数表
本节针对WMR非线性模型,运用本文设计的IT2FLC对其进行轨迹跟踪控制,并且通过QPSO、SelQPSO算法分别对IT2FLC的输入输出主次隶属函数参数分别进行优化。另外,本文还考虑系统不确定性(外部扰动)对控制效果的影响。同时,为了验证本文所提控制方法的优越性,分别与QPSO优化后的IT2FLC、未经优化的IT2FLC以及T1FLC控制方法进行对比。图5为优化前IT2FLC的输入输出主次隶属函数,图6为优化后IT2FLC的输入输出主次隶属函数。

图5 优化前IT2FLC输入输出隶属函数
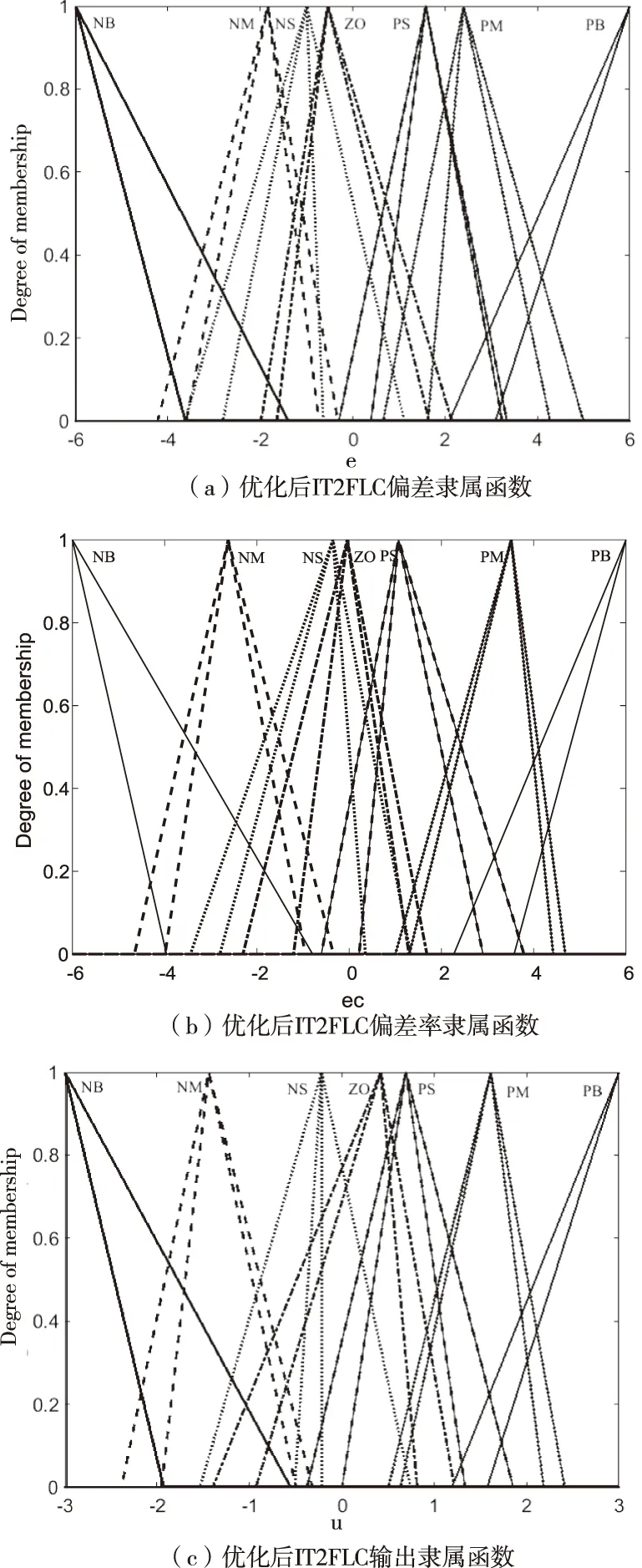
图6 优化后IT2FLC输入输出隶属函数
从图5、6中可以直观看出SelQPSO算法对IT2FLC输入输出主次隶属函数参数进行了优化。
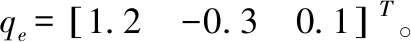
首先在不考虑外部扰动情况下,对比经过SelQPSO、QPSO算法优化的IT2FLC、未经优化的IT2FLC以及T1FLC算法跟踪控制效果,具体如图7,图中四种控制方法都能在一定时间内跟踪上期望轨迹,但从放大图中可以明显地看出,经过SelQPSO算法优化的IT2FLC跟踪效果优于另外三种控制方法。

图7 无扰动下WMR轨迹跟踪情况
图8展示了四种控制方法在跟踪过程中误差变化情况,可以直观看出与另外三种控制方法相比,经过SelQPSO算法优化后的IT2FLC在到达期望位姿后具有更小的超调量,且系统响应速度更快。图9展示了在跟踪控制过程中,WMR的线速度与角速度分别在四种控制方法下变化情况,可以明显看出,WMR的线速度与角速度在经过SelQPSO算法优化后的IT2FLC控制方法下,具有更小震荡。

图8 无扰动下WMR位姿误差变化曲线
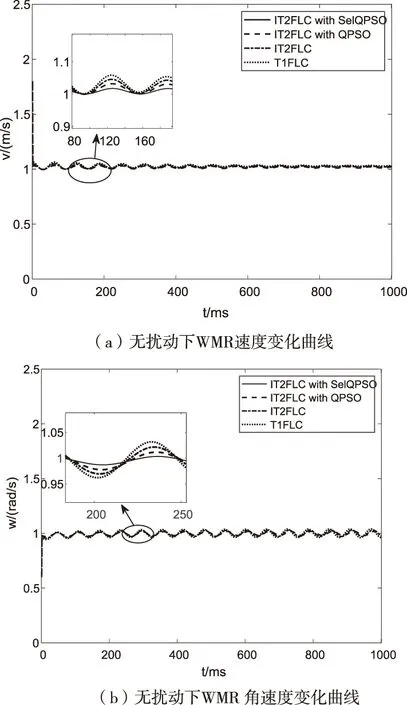
图9 无扰动下WMR速度与角速度变化曲线
接下来考虑在有外部扰动情况下。当t=13s时,即WMR达到稳定状态后,通过外部扰动使其偏离跟踪轨迹。从图10局部放大图可明显看出,与另外三种控制方法相比,经过SelQPSO算法优化的IT2FLC,在遇到干扰后可以更快地跟踪上期望轨迹,从图11、图12可以直观地看出,在遇到外部扰动时,本文所提的控制方法使系统拥有更快的反应速度、更强抑制干扰能力以及更好的鲁棒性。
图10 有扰动下WMR轨迹跟踪情况
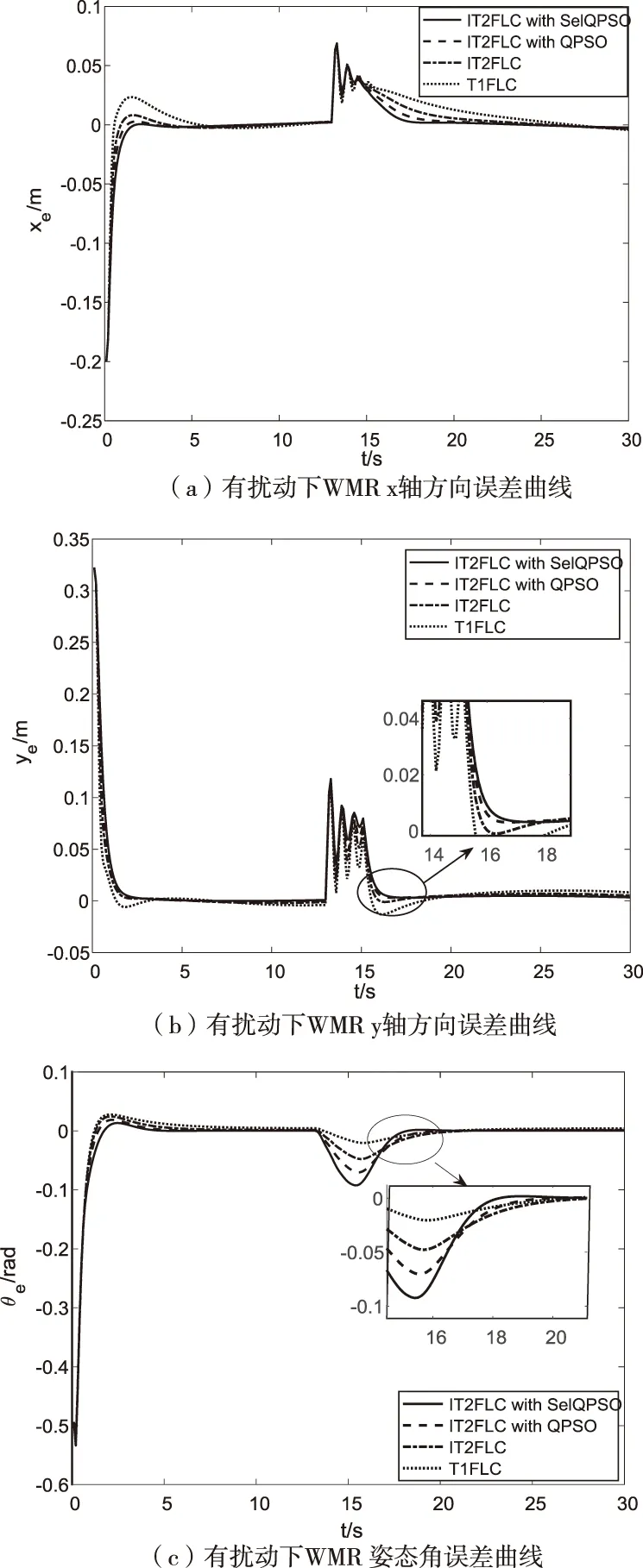
图11 有扰动下WMR位姿误差变化曲线
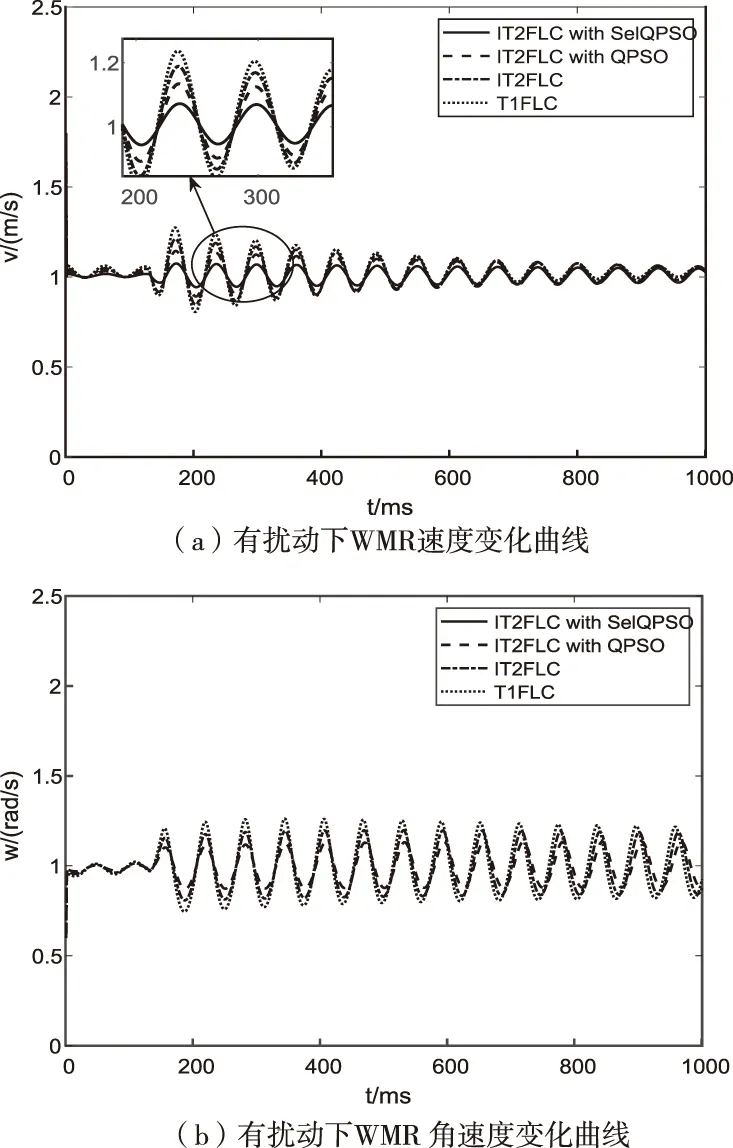
图12 有扰动下WMR速度与角速度变化曲线
为了进一步验证SelQPSO算法的优越性,通过评价函数对经过SelQPSO、QPSO算法优化的IT2FLC、未经优化的IT2FLC以及T1FLC算法进行平均方差积分(ISE)、误差绝对值积分(IAE)、误差绝对值(ITAE)计算,计算结果见表3,其中经过SelQPSO算法优化后的IT2FLC具有更小的评价指标,因此经过SelQPSO算法优化的IT2FLC对WMR跟踪控制优于经过QPSO算法优化的IT2FLC、未经优化的IT2FLC以及T1FLC算法。
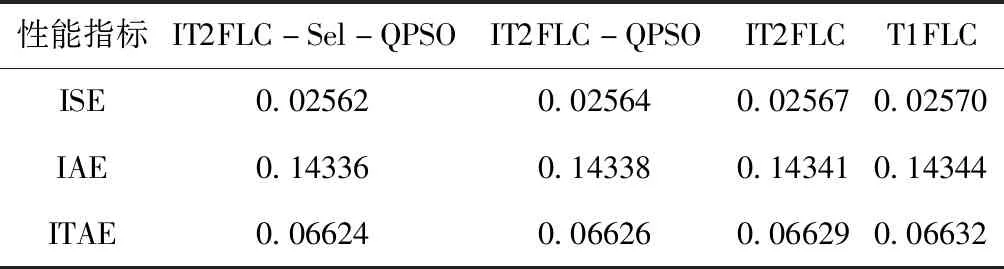
表3 控制算法性能指标对比表
7 结论
本文针对WMR轨迹跟踪问题,设计了IT2FLC,虽然IT2FLC能对WMR进行轨迹跟踪控制,但是其模糊规则中模糊集参数通过传统方法选择会影响控制精度,本文针对此问题,分别采用QPSO算法、改进的QPSO算法(SelQPSO)对模糊集参数进行优化。仿真结果表明,经过 SelQPSO算法优化的IT2FLC控制效果要优于QPSO算法,通过与未经优化的IT2FLC和T1FLC算法对比表明,本文所提的控制方法有更好的控制效果。此外,本文考虑了外部扰动对控制效果的影响,仿真结果表明,经过SelQPSO算法优化的IT2FLC使系统拥有更佳的抑制扰动能力、更快的反应速度以及更小的震荡。未来进一步工作重点是结合硬件实现算法,通过实验验证本文所提方法的有效性。
