基于神经元控制的无刷电机调速建模仿真
2021-12-10林京君
亓 芳,林京君
(1.吉林建筑科技学院电气信息工程学院,吉林 长春 130114;2.长春工业大学电气与电子工程学院,吉林 长春 130000)
1 引言
在传动装置和伺服系统中,直流电动机显示出电动机调速范围广、机械性能优良、控制效果好等优点,同时,直流电动机在实际应用过程中也会产生机械摩擦,对直流电动机造成一定程度的损坏,严重时甚至导致电动机瘫痪,另外,直流电机维修难度大,投资高,在实际生产和应用中受到很大限制,无刷电机应运而生。相较于直流电机来说,无刷电机装置结构更为简单,还采用了永磁材料作为转子材料,极大的降低了电机自身的质量,并提升了电机的可靠性能。为了适应社会生产力的需求,无刷电机也在不断的升级,现今使用的无刷电机具备重量轻、体积小、无励磁损耗、效率高、控制方式简便等特征[1],在实际应用中逐步替代了传统的直流电机,而如何精确的控制无刷电机速度是现今无刷电机发展与应用领域的重点研究课题之一,对此文献[2]在高性能高精度的控制要求条件下,提出了一种神经网络在线整定的PID控制算法,结合PSO对神经网络进行改进优化,响应性能更好,速度波动更小,但是其整体运算时间较长。文献[3]在分析无刷直流电机数学模型的基础上通过施加不同控制策略建立了无刷直流电机控制系统仿真模型,加快了实际系统的设计和调试过程,其最优解获取过程不明确。
无刷电机在运作过程中,经常处于启动、制动、反转的过渡阶段,如何减少这一阶段的时间,充分发挥无刷电机的性能,是无刷电机调速的根本。现有无刷电机调速方法由于自身算法的局限性,容易陷入局部极小值,并且收敛速度较慢,导致其存在着无刷电机调速实时性差、转矩波动幅度小等缺陷,故提出基于神经元控制算法的无刷电机调速建模仿真研究。神经元控制算法是工业控制过程中常用的控制算法,其具备操作简便、实现简易的优势,能够对一些工业过程进行极为有效的控制[4],希望通过神经元控制算法的应用,有效的提升无刷电机的调速性能,为无刷电机的应用与发展提供一定的帮助与参考。
2 无刷电机调速方法研究
2.1 无刷电机数学模型构建
为了更加精确的对无刷电机进行调速控制,首要的任务即为构建无刷电机数学模型,具体模型构建过程如下所示:
为了简化此研究过程,设定无刷电机结构为三相对称结构,不将无刷电机的凸极效应考虑在内。无刷电机定子绕组采用的是三相星型接法,则每相绕组具备一致的电感值与电阻值,可以将其等效为电感、电阻与反电动势串联而成,无刷电机主电路采用的是三相桥式逆变电路[5]。无刷电机工作制度为二二工作制,指的是利用单极性PWM方式,忽略齿槽因数与换想重叠的不利影响。
则三相绕组的电压平衡方程表达式为

(1)
式(1)中,ua、ub与uc分别表示每相相对于直流母线零电平的端电压;r表示定子相绕组电阻;ia、ib与ic分别表示定子相绕组电流;L表示每相绕组的自感;M表示每两相绕组间的互感;p表示微分算子;ea、eb与ec分别表示定子相绕组电动势。
由于无刷电机中的三相绕组连接方式为星形,并且没有中线,则认定定子相绕组电流相加等于零,即ia+ib+ic=0,并且存在着Mib+Mic=-Mia。则式(1)可以转换为
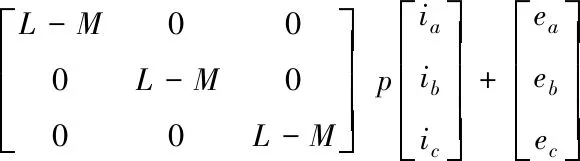
(2)
无刷电机电磁转矩由转子磁钢形成的磁场与电子绕组中的电流相互作用而产生的。无刷电机的定子绕组形成的电磁转矩方程为

(3)
式(3)中,Te表示无刷电机形成的电磁转矩;ω表示无刷电机的机械转速。
由式(3)可知,无刷电机电磁转矩方程与常规电机有一定程度的相似,电磁转矩大小均与电流幅值及磁通成正比例关系,因此无刷电机转矩控制即可通过控制逆变器输出方波电流幅值实现[6]。为了产生稳定的电磁转矩,要求定子电流为方波形式,并且方波每半个周期内,电流持续时间为120度,相对应的梯形波反电动势也为120度,方波与梯形波必须严格保持一致[7]。
在任何时间上,定子只存在两相导通,则定子功率为
Pe=eaia+ebib+ecic
(4)
此时可以将式(3)转换为
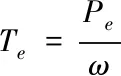
(5)
则无刷电机的运动方程式为

(6)
式(6)中,TL表示负载转矩;B表示阻尼系数;J表示无刷电机的转动惯量。
上述公式即构成了无刷电机数学模型,为后续无刷电机的调速模型构建打下坚实的基础。
2.2 电机参数辨识与估计
为了提升无刷电机调速的性能,需要精确的对电机参数进行辨识与估计,具体过程如下所示:
在无刷电机调速过程中,通常需要确定电机的转子电阻、磁链等信息,以此来对电机速度进行定向控制。但是,在无刷电机实际运作过程中,转子电阻与磁链信息测量难度非常大,故只能通过相应模型对其进行辨识与估计[8]。
此研究采用神经网络模型来辨识并估计无刷电机参数,具体示意图如图1所示。
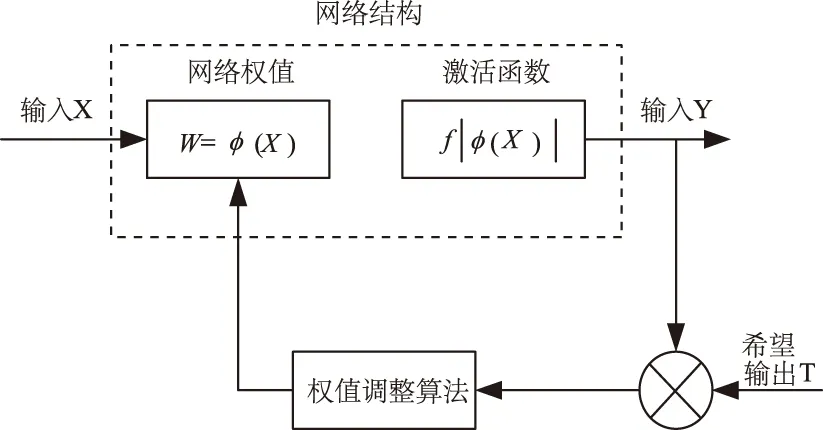
图1 无刷电机参数辨识与估计示意图
如图1所示,则无刷电机参数辨识与估计具体步骤如下:
步骤一:将全部的网络权值随机的、均匀的进行分布,并提取其中较小的值;
步骤二:采集实测的输入与输出数据,其共同构成了训练样本;
步骤三:将步骤二获得的训练样本输入到神经网络模型中,通过计算并输出Y;
步骤四:误差函数计算,其计算公式为
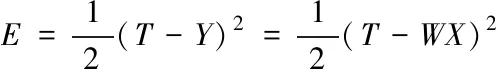
(7)
步骤五:依据多种权值学习调整算法对网络权值T进行修正;
步骤六:对前后两次训练的网络权值误差进行计算,计算公式为
εi=Wi+1-Wi
(8)
将式(8)计算结果与给定误差ε进行比较,若εi≤ε,则神经网络模型训练停止。同时比较训练次数n,若训练次数大于或者等于给定的终止次数,则神经网络模型训练停止,以此方式来防止模型不收敛情况的发生;
步骤七:将训练好的神经网络模型作为无刷电机参数辨识与估计的模型[9]。
2.3 电机数字信号处理
依据上述辨识与估计的无刷电机参数为基础,采用型号为28335的DSP芯片处理无刷电机数字信号,为最终的无刷电机调速控制做准备。
28335DSP芯片是一种数字信号处理器,实质上是一个可编程、超大规模的集成电路,通过内部硬件与可下载软件来实现复杂的数字信号处理功能[10]。28335DSP芯片具备多种功能,则其包含了多个引脚,定义情况如表1所示。

表1 28335DSP芯片引脚定义表
28335DSP采用的哈佛结构,其是一种并行体系结构,具备独立的数据与程序存储空间,允许CPU同时执行指令与数据操作,极大的提升了DSP的数字信息处理效率[11]。28335DSP哈佛结构如图2所示。

图2 28335DSP哈佛结构图
另外,28335DSP还包含专用的硬件乘法器,使其能够在一个单指令周期内完成一次或者多次乘法运算,从而极大的提升了DSP芯片的运算效率。
28335DSP芯片采用Q格式对运算数值进行定标,其浮点数与定点数之间的转换关系为

(9)
式(9)中,xq表示浮点数;x表示定点数;(int)与(float)表示转换函数。
2.4 无刷电机调速控制
以经过28335DSP芯片处理后的无刷电机数字信号为基础,基于神经元控制算法制定无刷电机调速步骤,实现无刷电机的调速控制,具体实现过程如下:
基于神经元控制算法控制无刷电机调速仿真模型如图3所示。
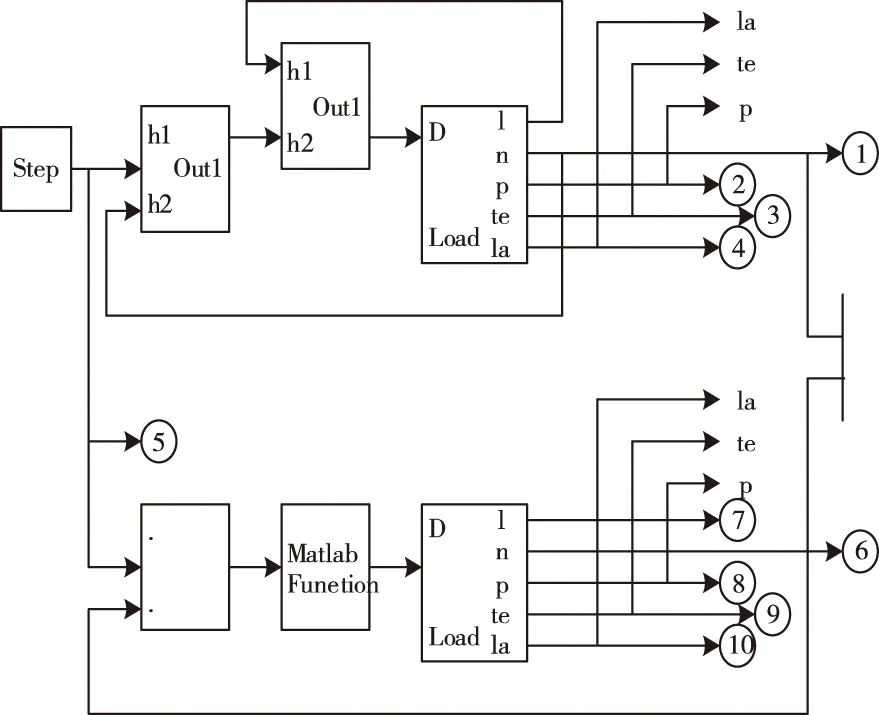
图3 无刷电机调速控制仿真模型
基于神经元控制算法进行无刷电机调速控制步骤如下所示:
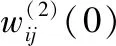
步骤二:采集训练样本获得r(k)与y(k),同时计算e(k)=r(k)-y(k);
步骤三:对步骤二获得数据进行统一化处理,以此作为神经元网络的输入;
步骤四:计算神经元控制算法的可调参数KP(k)、KI(k)与KD(k);
步骤五:计算神经元控制算法的控制输出u(k),以此为基础,进行无刷电机调速控制;
步骤六:在权值更新一次后,再次计算误差e(k+1),若满足e(k+1) 步骤七:设置k=k+1,返回步骤二。 通过上述过程最终实现了无刷电机调速的控制,为无刷电机的应用提供支撑,也为无刷电机的发展与研究提供一定的参考[12]。 为了验证提出方法与文献[2]方法的性能差异,采用MATLAB软件建模仿真设计对比实验,具体的实验过程如下所示: 利用Simulink提供的仿真模型库,依据构建的无刷电机数学模型构造出调速仿真模型,为仿真做准备,具体如图4所示。 图4 无刷电机调速仿真模型 为了明确无刷电机调速的控制,获得客观的实验结果,必须明确无刷电机转子位置与反动势之间线性关系,如表2所示。 表2 电机转子位置与反动势关系表 如表2所示,k表示反动势系数;ω表示转速信号。 实验参数是仿真顺利进行的基础与前提,因此为了保障仿真的顺利进行,依据无刷电机调速控制需求确定仿真参数,如表3所示。 表3 仿真参数设置表 依据上述构建的无刷电机调速模型以及确定的仿真参数进行实验,通过调速控制实时性与转矩波动幅度来显示提出方法的性能,具体实验结果分析过程如下所示: 通过实验获得方法性能数据如表4所示。 表4 方法性能数据表 如表4(1)数据所示,提出方法调速时间范围为0.9857s-1.2344s,文献[2]方法调速时间范围为2.0109s-2.5410s。通过对比发现,提出方法调速时间得到了极大的缩减,表明提出方法调速实时性更好。 如表4(2)数据所示,提出方法转矩波动幅度范围为0.10Nm-0.15Nm,文献[2]方法转矩波动幅度范围为0.01Nm-0.05Nm。通过对比发现,提出方法的转矩波动幅度更大。 1)利用神经元控制算法提出了一种新的无刷电机调速方法,并利用建模仿真验证所提方法的性能,能够为无刷电机的应用与发展提供一定的理论参考价值。 2)调速实时性更好,转矩波动幅度范围为0.10Nm-0.15Nm,极大地提升了调速实时性与转矩波动幅度,充分证实了提出方法无刷电机调速效果更好,为无刷电机应用领域的扩张提供有力的支撑。3 建模仿真与结果分析
3.1 无刷电机调速模型模型建立


3.2 实验数据准备

3.3 实验结果分析
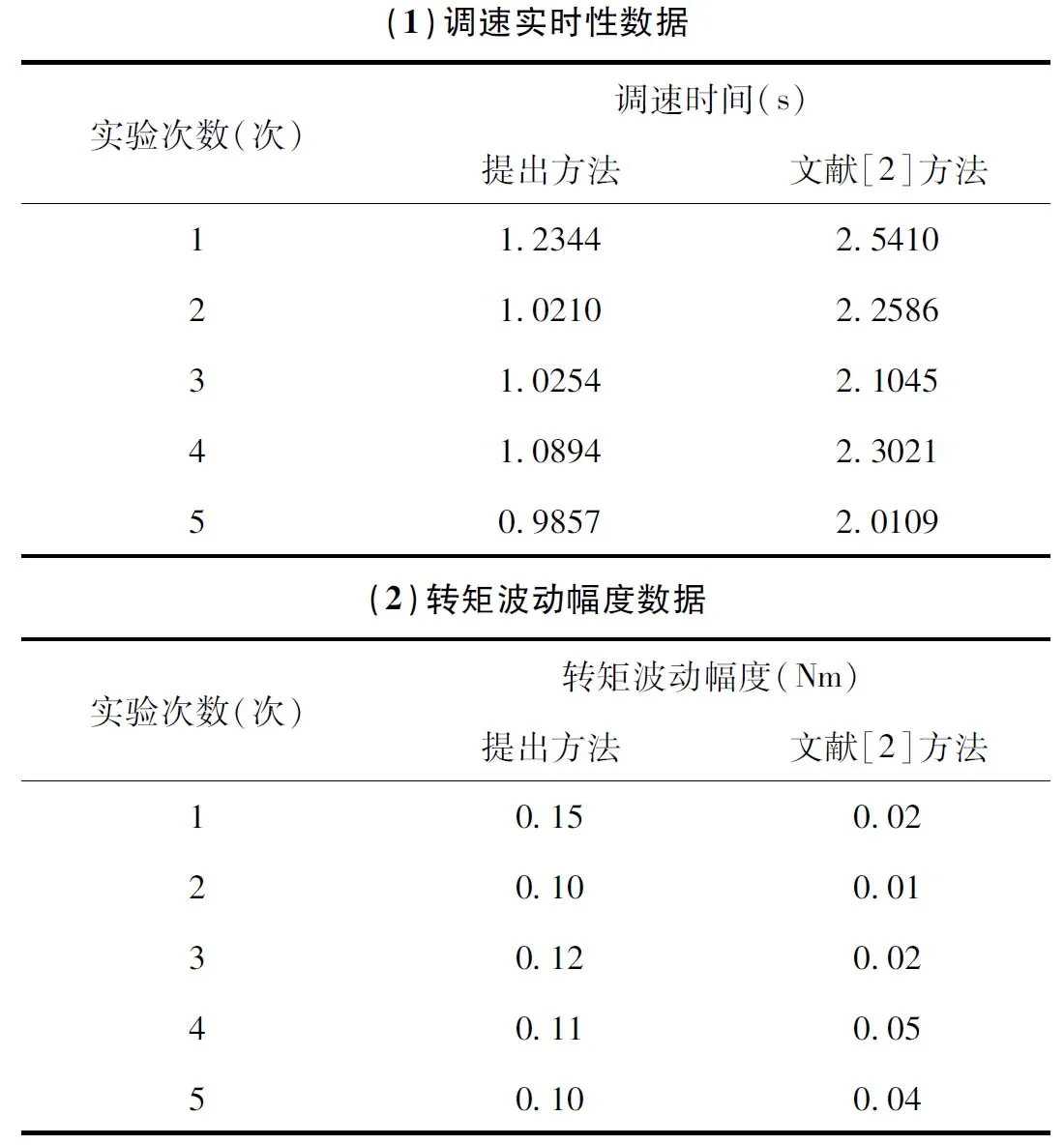
4 结束语
