基于PSO优化的永磁直线同步电机混沌滑模控制

黄俊豪，杨俊华，陈海峰，蔡浩然

(1.广东工业大学自动化学院，广东 广州 510006；2.广州市市政工程设计研究总院有限公司，广东 广州 510000)

1 引言

永磁直线同步电机(permanent magnet linear synchronous machine，PMLSM)利用动子直线运动切割磁场发电，没有中间传动装置，结构简单，转换效率提高[1-3]，已应用于波浪发电系统等相关研究当中[4-5]。永磁同步直线电机运行过程中，特定参数条件下，其电流、转速及转矩会产生短时剧烈振荡及不规则噪声，进入控制性能极不稳定的混沌运行状态[6-8]，对发电系统正常运行及并网产生不良影响。PMLSM是一个强耦合复杂机电系统，海洋工作环境不确定性大，PMLSM波浪发电系统输入不稳定，更易进入混沌状态[9]，需研究其混沌特性及稳定控制方法。

通过设计优化定子铁芯、绕组，转子永磁体，永磁同步电机在低速运行时可以取得较好的混沌控制效果[10]，但电机设计通用性较低。文献[11]改进耦合电机系统的混沌模型，基于三对角结构矩阵稳定性理论提出一种高速混沌控制器，实现了发电机系统混沌控制，并可通过调整控制参数值缩短瞬态时间，消除混沌，但如何确定控制参数值是一个亟需解决的问题。为抑制电机混沌，文献[12]将永磁同步风电系统转为类洛伦兹模型，提出自抗扰控制(ADRC)方案，可降低对精准数学模型的依赖，保证转子速度快速跟踪期望值，解决参数不确定问题，对直线电机有借鉴意义。文献[13]将电机模型转化为Brunovsky形式，应用扩展状态观测器优化滑模混沌控制，提高系统应对未知状态和不确定性能力，鲁棒性增强，但坐标变换过程复杂。为抑制永磁同步电动机运行过程中的混沌现象，文献[14]构造PMSM矢量操控系统，提出了非奇异快速终端滑模混沌控制方法，减弱了对速度传感器的依赖性。文献[15]提出一种自适应滑模控制策略，使PMLSM在参数不确定条件下可脱离混沌。滑模控制是实现混沌控制的有效方法，但控制参数改变对控制效果影响较大，需解决最佳控制参数寻优问题，智能算法正当其时。针对风力机最大功率捕获问题，文献[16]应用粒子群算法优化滑模控制器参数。

通过建立PMLSM数学模型，运用状态反馈，获得d-q轴解耦数学模型，分析电机混沌现象。为实现电机混沌脱离及稳定控制，设计滑模控制方案。利用BP神经网络拟合逼近能力，研究不同参数滑模控制效果。结合粒子群优化(PSO)与滑模控制率，寻找最优控制参数，使控制率更优，实现PMLSM更快脱离混沌并达稳定。

2 PMLSM数学模型

2.1 PMLSM混沌状态方程

PMLSM的结构如图1示。与永磁同步电机相似，初级固定，次级动子做直线运动，永磁体交替分布在运动路径上。通入三相正弦交流电后，产生行波磁场，磁场方向同动子运动方向相反。

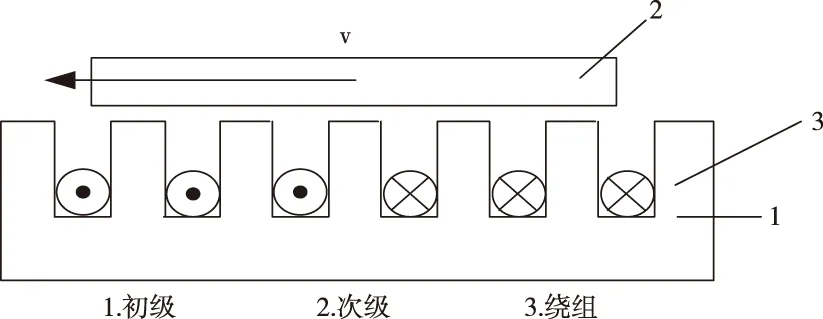
图1 永磁直线电机结构图

为建立PMLSM数学模型，假定铁芯不饱和，动子上无阻尼绕组，不计谐波与涡流损耗[17]。考虑边缘效应，通过派克变换及放射变换[15]，电机混沌数学模型为

(1)

忽略式(1)中的上标，可得简化表达式

(2)

2.2 PMLSM的解耦数学模型

由式(2)可见，d-q轴电压电流相互耦合，难以直接进行控制，利用状态反馈解耦，构造解耦矩阵，解耦式(2)[18]。

图2 状态反馈解耦系统

(4)

3 PMLSM混沌分析

3.1 混沌识别

混沌识别是混沌分析中一个关键步骤。Lyapunov指数是目前混沌判别中一种最常用的有效方法。对于混沌系统来说，初值极细微改变，都可能会使相关运动轨迹逐渐呈现指数级增长分离，导致系统进入混沌状态。Lyapunov指数能更准确反映混沌运动轨迹的平均发散指数率。当混沌系统Lyapunov指数小于0时，系统相体积呈缩小趋势，渐进趋于稳定状态；当该指数大于0时，系统相体积则呈现增大趋势，运动轨迹逐渐分离，并最终进入混沌状态。因此，当系统Lyapunov指数至少出现一个正值时，系统便会进入混沌状态，呈现一定区域范围内系统运动轨迹的有界性与随机性[19-20]。计算系统最大Lyapunov指数，判断其正负值，即能判断系统是否进入混沌状态。

Wolf算法，可追踪计算两点的运动轨迹及其距离变化值Δd，若Δd随时间不断增大，则系统会进入混沌状态，计算方法为[21]

(5)

其中ε为积分步长，d0为运动两点初始距离。

3.2 PMLSM混沌分析

根据PMLSM混沌数学模型，进行仿真建模，当参数σ和γ取不同值时，计算最大Lyapunov指数，结果如图3示。

图3 PMLSM最大Lyapunov指数图

分析图3，最大Lyapunov指数随σ和γ变化而变化，σ影响相对更大一些。当σ逐渐减小至5左右时，最大Lyapunov指数穿过零平面变为负值，系统脱离混沌状态。

PMLSM混沌状态下的d-q电流与转速变化如图4示，并由此可知，进入混沌状态下的电机电流、转速会在一定区域范围内无序地振荡。

图4 PMLSM的混沌响应

4 PMLSM的滑模控制律设计及优化

4.1 滑模控制率设计

滑模变结构控制受系统参数影响，但不受外界波动因素影响，鲁棒性强。

(6)

求导可得

(7)

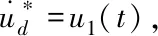
(8)

对式(10)求导得

(9)

其中c1为控制参数，大于零。

针对式(11)构造Lyapunov函数

(10)

求导得

(11)

设计控制率

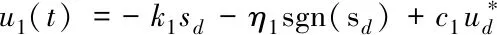
(12)

式中k1>0，η1>0。

(13)

对上式求导，得

(14)

构造Lyapunov函数

(15)

求导得

(16)

设计控制率b(t)

(17)

式中k2>0，η2>0。

至此，完成PMLSM系统控制率设计。

4.2 BP神经网络拟合控制参数全局效果

式(14)与式(19)给出的控制率中，共有6个可控参数c1、k1、η1、c2、k2、η2，研究可知，η1、η2对控制率影响较小，但其余参数的细微变化，都会影响系统响应时间及超调量等。

BP神经网络学习逼近能力强大，可拟合任一非线性函数，选用常见的三层网络，预测滑模控制率控制参数，结果如图5示。

图5 PMLSM响应时间图

图6 PMLSM超调量图

由图5、6可知，控制参数的细微变化会对系统响应时间与超调量造成较大影响，存在多个局部最优值。也就是说，传统经验法可确定局部最优控制参数，但无法确定全局最优控制参数。

4.3 PSO优化滑模控制参数

粒子群算法(PSO)搜索速度快，可迅速找出最优解，已被广泛应用于工业控制领域优化[22]。粒子能够依据个体与全体历史最优适应值不断迭代，来更新自身速度位置。PSO位置与速度关系

(18)

其中，ω为惯性权重，c1、c2是学习速率，r为一个随机数字，xi、vi是第i个粒子位置及运动速度，pbest、gbest分别是粒子、粒子群的历史最优位置。PSO工作流程如图7示。

图7 PSO工作流程图

针对优化目标控制率，要求系统响应时间尽可能短、超调量尽可能小。根据式(4)，PMLSM已实现d-q轴解耦，d、q轴可独立控制，于是设置适应值函数：

(19)

式中，Td、Tq、Tv、Od、Oq、Ov分别为d、q轴电流与转速v的响应时间及超调量。

5 仿真验证

利用PSO对滑模控制率控制参数优化适应值曲线如图8示。将优化后的控制参数输入到系统控制率中，结果如图9示。

图8 最优适应值曲线

由图9可知，所提方案可使电机脱离混沌状态并达到给定稳态目标值，PSO参数优化后的滑模控制率耗时更短，超调小，控制效果更好。

图9 滑模控制算法及优化后滑模控制算法下的PMLSM动态响应

6 结论

通过建立PMLSM解耦数学模型，证明电机运行过程中可能会进入混沌状态，为此设计滑模控制器，实现混沌控制。利用BP神经网络拟合滑模控制参数，利用PSO算法优化控制率，确定最优控制参数。仿真结果表明，滑模控制策略能够实现PMLSM混沌脱离与稳定控制，经PSO优化后的滑模控制率，响应时间及超调量小，控制效果更佳，鲁棒性提高。