基于蒙特卡洛的动车组差动保护可靠性研究

孟建军，赵文涛

(1.兰州交通大学机电技术研究所，甘肃 兰州，730070；2.甘肃省物流及运输装备信息化工程技术研究中心，甘肃 兰州，730070；3.甘肃省物流与运输装备行业技术中心，甘肃 兰州，730070)

1 引言

保护对于电力系统而言是非常重要的一环，而动车组作为高可靠性要求的产品保护更是必不可少。差动保护系统是动车组牵引电力系统的主保护，其安全可靠运行对于整个动车组的运营至关重要。然而我国铁路部门对其采用的检修方案仍是“定期维修”，造成了人力、物力、财力的巨大浪费[1]，急需相关可靠性理论作为其维修方案的参考。

针对动车组差动保护系统组件数量多、离散程度高、结构复杂[2]等特点，选用故障树分析法来对其进行可靠性分析，为表示动车组差动保护系统中的时序逻辑，引入动态逻辑门，故采用动态故障树来对动车组差动保护系统进行可靠性的量化与评估。

1991年，Dugan等最早提出了动态故障树分析法的概念[3，4]，而国内的熊小平等重点考虑了冗余的动态特性，建立动态故障树对变电站保护系统进行了可靠性分析[5]。对于动态故障树的求解，1992年，Souza等首次将其转化为马尔可夫模型使用解析法求解[6，7]，近年来周广林等对其进行了优化与扩展，融合了三角模糊数并在矿井作业中得到了应用[8]，但仍存在状态爆炸、对于组件的故障率只能设为常数而实际中故障率随时间变化等问题。蒙特卡洛法更多的是一种思想，利用大量的样本数据进行仿真，对其结果实行概率分析，进而解决问题的思想[9]，而系统规模和状态维数的爆炸性增长对蒙特卡洛法的运算复杂度影响较小[10，11]。故本文对动态故障树模型采用蒙特卡洛仿真方法求解，能够很好的解决上述问题。

2 动车组差动保护系统简介

基于基尔霍夫定理实现的动车组差动保护装置用于动车组牵引系统的过压、过流保护，牵引主电路正常工作时，牵引变压器原边输入端和输出端的电流互感器检测电流差为零，即差动电流为零或在整定范围以内；当差动电流值超过整定值时，触发差动保护将牵引变压器与故障电流断开，实现牵引电力系统的保护[12]。其接线原理如图1所示。

图1 差动保护系统原理示意图

3 动车组差动保护系统动态故障树的建立

针对动车组差动保护系统，收集研究其故障机理[13]，如差动保护系统使用的电流互感器铁芯类型为开口式，长期工作会导致其发生锈蚀、质量下降、交合处气隙增大、铁芯磁导率下降等使得线路误差增大超过限定值，进而导致差动保护误动[14]。确定以动车组差动保护系统故障为顶事件，以电流互感器铁芯故障、电流互感器绕组故障、分接开关故障为中间事件建立三个故障子树，然而在电流互感器中，无论是一次绕组还是二次绕组，若发生过电压的情况，则一定会导致绕组局部过热、局部场强增强、局部场强集中等故障的发生，这是经典故障树无法表达出来的时序性，故在上述故障树中加入动态逻辑门绘制如图2-6所示的动态故障树。

图2 差动保护系统动态故障树

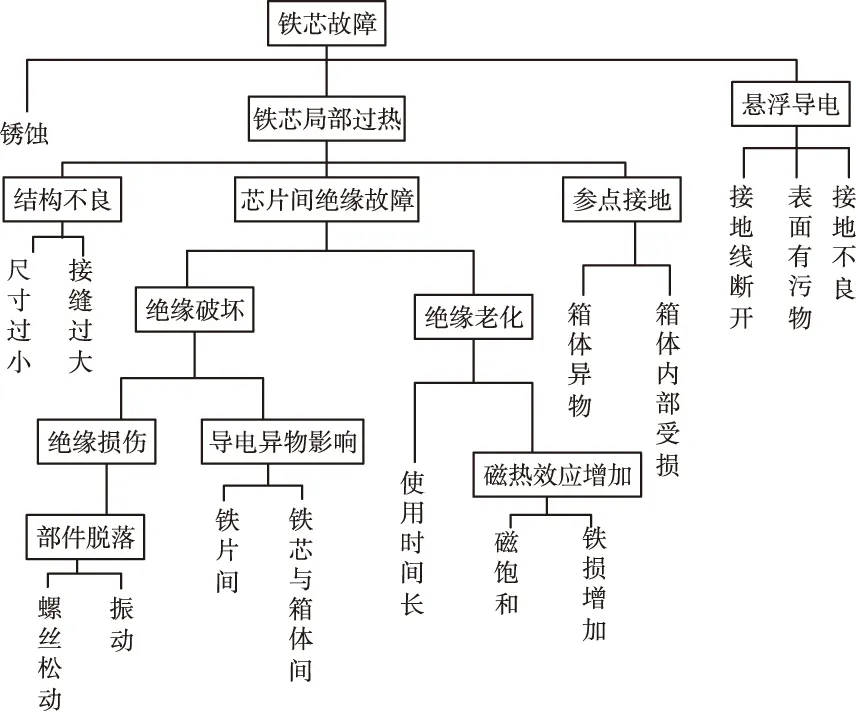
图3 电流互感器铁芯故障A子树

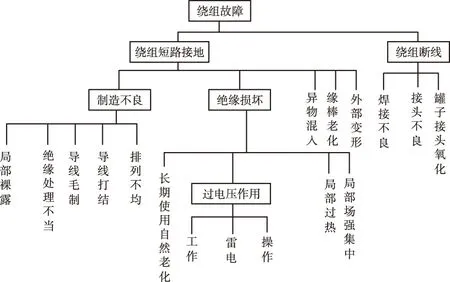
图4 电流互感器绕组故障B子树

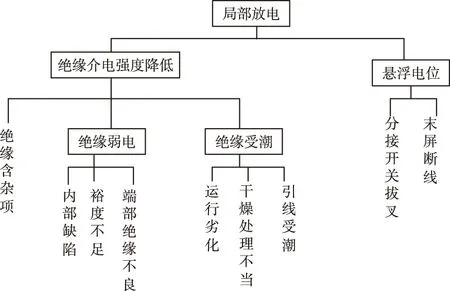
图5 B子树补充a子树

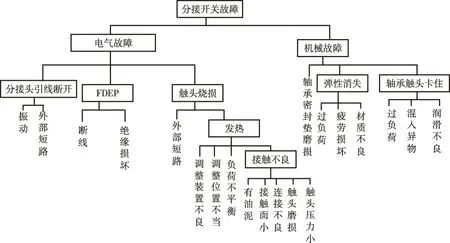
图6 分接开关故障C子树

4 动车组差动保护系统可靠性分析

目前在可靠性分析理论中，认为所收集的元件故障运维数据是完全数据，即均符合收集数据要求的各项标准。但这与实际情况有很大的出入。收集到的故障数据并不都可以体现元件故障的特性。一些故障数据可能仅代表其寿命不小于该数值，无法得知确切寿命，这样的数据称为截尾数据。若并不是所有元件都从同一时间开始数据收集，而且在收集过程中，一些元件由于某种原因尚未故障中途撤离，如部分元件信息中途丢失、在现场收集时某些元件尚未失效等，这样的截尾数据则成为随机截尾数据。对于动车组差动保护这样的寿命周期较长的安全系统，由于元件的定期维修或更换等原因，收集到的故障样本数据更符合上述随机截尾数据的特征，且为使本文所作的研究更具有普遍意义，认为所使用的数据均为随机截尾数据。

鉴于篇幅限制，本文将以分接开关故障C子树中的电气故障动态子树为例，对动车组差动保护系统的可靠性研究进行详细的阐述。

4.1 元件故障分布参数估计

为更好地利用先验知识和现场组件故障数据统计的期望，本文采用了马尔可夫蒙特卡洛方法，结合贝叶斯估计法和最大似然估计优点的混合算法。不同的元件根据各自的先验知识与现场故障数据统计样本，选取不同的分布模型进行故障分布参数估计。对于电气故障子树而言，其各个底事件均为电气常发故障，故障分布更符合二参数威布尔分布，故认为电气故障子树中的底事件故障分布均为二参数威布尔分布。

二参数威布尔分布的故障概率分布函数为

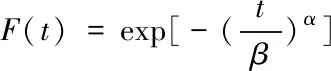
(1)

其概率分布密度函数为

(2)

本文认为所采集到的故障数据均为随机结尾故障数据，可整理为

(t1，δ1)，(t2，δ2)，(t3，δ3)…(tn，δn)

(3)

δi=0为截尾数据，而δi=1为正常故障数据，本文以底事件62外部短路为例，其数据样本如表1所示．

表1 底事件62外部短路的截尾故障样本

其中*数据代表截尾数据。

鉴于直接采用贝叶斯方法的后验分布进行统计推断非常困难，本文建立一个稳定分布与后验分布一致的马尔科夫链，当其收敛时便可以将其模拟值作为从后验分布中抽取的样本。

电气故障子树中的底事件故障率均会随着时间缓慢增加，如日久消耗等原因。极限情况为其故障率与时间呈线性关系，此时参数α=2；若其故障率与时间无关，此时参数α=1。故有理由相信对于参数α，先验概率在1.5两侧以同样的速度递减。此时α的先验边缘概率估计函数为

(4)

故参数α的先验概率分布取以1.5为中点的三角分布。其抽样公式如下

α=1+0.5(R1+R2)

(5)

其中R1，R2为在电脑上产生的[0，1]上均匀分布的随机数。

对电气故障动态子树的底事件62外部短路发生时间样本进行统计分析，可得其故障时间期望为1000小时到1700小时之间，故该底事件的故障时间期望函数为

(6)

故参数β的估计值抽样公式如下

(7)

其中R3为在电脑上产生的[0，1]上均匀分布的随机数。

故电气故障子树的底事件62外部短路二参数威布尔分布的参数联合先验概率为

(8)

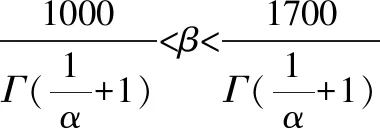
前文提到当构建的马尔科夫链收敛时进行取样便可模拟解决贝叶斯方法的实现困难之处，接受概率如下

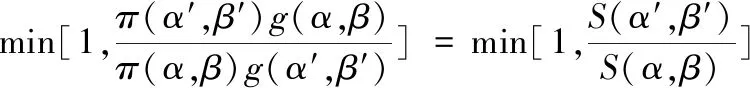
(9)

其中π(α，β)为贝叶斯后验概率，正比于S(α，β)与g(α，β)的乘积，系数为标准化常量。

其中S(α，β)为二参数威布尔分布的最大似然函数，公式为

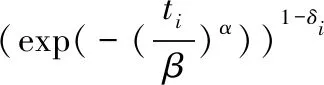
(10)

首先根据先验知识选取α为三角分布初始值为1.5，β为伽马分布初始值为1350，迭代次数选为10000次，根据式(5)和(7)抽取抽样值α′β′,以接受概率式(9)接受抽样值，即若抽样值与初始值的最大似然函数之比大于1则接受抽样值，否则以比值的概率接受抽样值，否则拒绝抽样值。直到迭代结束。图7为参数α的接受迭代抽样值，图8为参数β的接受迭代抽样值。

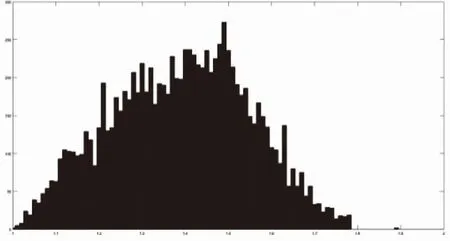
图7 参数α的迭代结果直方图

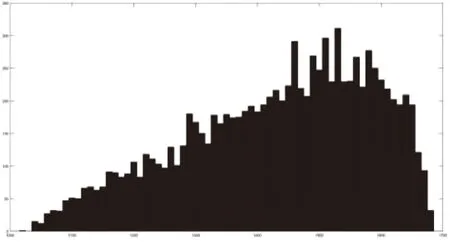
图8 参数β的迭代结果直方图

在10000次迭代中，有5736次参数抽样值可以被接受，故舍弃被拒绝的抽样值，对迭代过程中所有参数的接受抽样值取算数平均值即为α和β的估计值。结果为α=1.39，β=1431.1。

其它底事件的失效概率分布参数估计过程与62外部短路的估计方法相同，结果如表2所示。

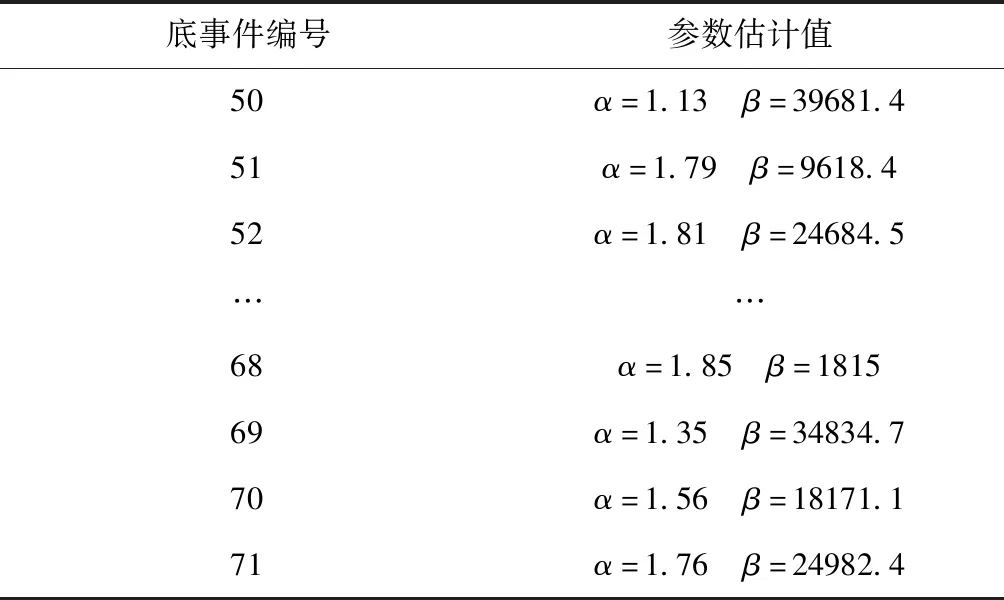
表2 电气故障动态子树各底事件的概率分布函数参数估计值

4.2 动车组差动保护系统动态故障树的蒙特卡洛仿真分析

本文所建立的动车组差动保护系统动态故障树具有底事件数量大、故障发生的时间长、概率分布函数复杂等特点，故采用仿真固定时间步长法，即按照一个固定的仿真时间间隔作为时间增量来进行仿真，以底事件的概率密度函数抽取底事件发生时间，与仿真时间做对比判断元件的状态，若仿真时间大于底事件发生时间则认为该事件发生，在每个时间间隔推进点上对各个事件的状态进行评估，更新整个动态故障树的仿真状态。

通过上面的计算已经得到了各底事件发生时间分布的参数估计值，采用反函数随机数抽取法来对发生故障的时间进行抽样，本文所设定的二参数威布尔分布的抽取公式为

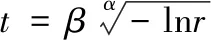
(11)

其中r为在电脑上产生的[0，1]上均匀分布的随机数。

将电气故障动态故障子树根据其时序逻辑转化为布尔运算函数

T=x52+x53+x54+x61+x62+…+x70+x71

(12)

输入为底事件是否发生，输出为顶事件是否发生。

输入抽样的各个底事件发生时间，按照固定步长法进行仿真，每经过一个时间间隔则与底事件发生时间进行对比判断底事件状态，带入布尔运算函数中计算顶事件状态。当顶事件发生时记录仿真时间，重复以上步骤直到设定的仿真次数。

在对电气故障动态子树顶事件进行仿真时，设定仿真次数为10000，时间步长为2小时。

统计在整个仿真过程中顶事件发生的次数及仿真时间，对仿真结果进行二参数威布尔分布曲线拟合，顶事件发生时间直方图与函数拟合曲线如图9所示。

图9 电气故障子树顶事件发生概率分布函数直方图和拟合曲线

故得到电气故障子树顶事件发生概率分布函数为

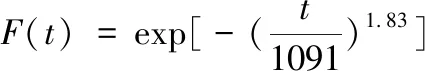
(13)

从图中可以看出，顶事件发生次数在运行1000小时左右最高，超过 3000小时次数逐渐趋近于0。

而整个动车组差动保护系统动态故障树顶事件发生概率分布函数为：

(14)

4.3 动车组差动保护系统元件的重要度分析

从布尔运算函数(12)来看，似乎在电气故障动态故障子树中，14个底事件对于顶事件发生的贡献度是一样的，而实际中不同底事件对于顶事件的重要度不相同也是不可能相同的，特定元件在系统的架构、位置的不同可能造成其影响系统安全可靠运行程度的不同，对动车组差动保护系统动态故障树进行重要度分析对系统设计、诊断及最优化分析时有相当大的作用，可根据各元件重要度决定系统检查、维护及故障检测执行的先后顺序，或是在系统改进时改进重要度较大的元件。

对于电气故障动态故障子树的重要度分析同样使用蒙特卡洛仿真方法，即数学模型算法。系统内包含诸多子树，底事件数量较大，系统的故障时间函数中参数包含每个元件的故障时间，重要度便可使用系统发生故障时间对组件发生故障时间的偏微分来表示

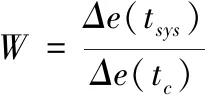
(15)

在保持其它底事件的发生时间抽样条件不变的情况下，仅改变某单个底事件的发生时间期望，然后使用蒙特卡洛仿真方法求解顶事件发生的时间期望，通过对比顶事件发生时间期望相对于初始状态的改变来计算该底事件的重要度。

重要度的求解较为简单，过程便不多赘述，动车组差动保护系统底事件重要度仿真结果如表3所示：

表3 动车组差动保护系统底事件重要度

由上述重要度仿真分析结果可知，对于动车组差动保护系统而言，底事件发生特性变化对顶事件发生概率分布重要度较大的是底事件1锈蚀、39谐振以及62外部短路。总体而言，绕组对于动车组差动保护系统重要度最大，分接开关的重要度最小。设法降低上述重要度较高的底事件发生概率可以有效提高系统的可靠性，在对动车组差动保护系统进行系统检查、维护及故障检测时可参考本文重要度的仿真分析结果，优先对绕组进行检测，重点关注是否发生了锈蚀、谐振以及外部短路等故障。

5 结束语

本文结合动车组差动保护系统的故障机理，完成了动态故障树的构建，采用了马尔可夫蒙特卡洛方法结合贝叶斯估计法和最大似然估计优点的混合算法来对动态故障树各个底事件的概率分布函数的参数值进行估计，构造顶事件的布尔函数，利用固定时间步长仿真法进行蒙特卡洛仿真分析求得顶事件发生的概率分布函数，证明了动车组差动保护系统可靠性较高，通过改变单一变量的方法系统各底事件对于顶事件的重要度进行分析，得出了绕组的重要度较高，在进行系统检查、维护及故障检测时可参考本文重要度的仿真分析结果，优先对绕组进行检测，重点关注是否发生了锈蚀、谐振以及外部短路等故障的结论，可作为制订动车组差动保护系统检修策略的参考。