基于无迹卡尔曼滤波单液流锌镍电池SOC估计

田曜荣，宋春宁，莫伟县

(广西大学电气工程学院，广西 南宁 530004)

1 引言

电池的荷电状态(SOC)是电池一项重要参数，准确的估计电池的SOC，可以防止电池过度充电和过度放电，提高电池的寿命和电池的工作性能，但由于电池的荷电状态(SOC)不可以如同电池的电压、电流、温度等物理量能直接测量，并且电池内部为复杂的电化学反应，在电池在工作过程中电池内部的能量变化呈现很强的非线性变化，这导致对电池的SOC估计是要考虑多方面问题，考虑不够的话会导致估算准确性低。目前常见的电池SOC有开路电压法、安时积分法、卡尔曼法等[1]，文献[2]中通过实际测试和理论计算确定全钒液流电池的容量，根据开路电压与SOC的关系来估计SOC。文献[3]将安时积分法与另一种校正初始值的算法相结合的方式来估计SOC，通过校正SOC的初值，来改善安时法在SOC初始值不准确时导致累计误差增大的问题，但这种方法需要精准的电池端电压来校正。文献[4-5]采用扩展卡尔曼滤波算法(Extended Kalman Filter，EKF)对电池SOC估计，但是利用泰勒展开将电池模型线性化处理导致了模型的精度降低，也大大的使计算量增加。

单液流锌镍电池作为单电解液电池，由于没有离子交换膜，不会出现正负极的电解液交叉污染的问题，且只需要一个泵机对电解液进行循环，降低液流电池的成本，提高了液流电池的循环使用寿命[6]。国内外学者也对它进行了许多的研究，2015年美国CUNY能源研究所提出在高电流密度的前提下，正极极化是改善单液流锌镍电池性能的关键障碍化[7]；防化院研究了单液流锌镍电池的电池性能与电极材料和电解液对电池性能的影响[8]；广西大学研究了不同的充电电流和充电容量与单液流锌镍电池性能的关系[9]。但目前关于锌镍单液流电池荷电状态估计的研究较少，本文作者针对单液流锌镍电池提出一种基于无迹卡尔曼滤波算法(Unscented Kalman Filter，UKF)的单液流锌镍电池荷电状态估计方法，为单液流锌镍电池高效、安全和长使用寿命的运行提供基础研究。

2 单液流锌镍电池等效模型

2.1 单液流锌镍电池介绍

本实验使用的单液流锌镍电池的正负极材料分别为氧化镍和镀锌电极，电解液由ZnO、KOH和LiOH按一定比例配置而成(ZnO为0.8mol/L，KOH为10mol/L，LiOH为0.25mol/L)，电池单体容量为14Ah，充放电的截止电压分别为2.1V和1.2V，电池温度范围为5℃到40℃，原理图如图1所示。电池内部的电化学反应为

正极反应:

(1)

负极反应:

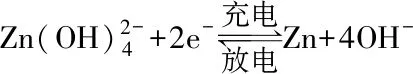
(2)

2.2 建立单液流锌镍电池等效模型

搭建电池等效模型是为了研究电池外部特性(如电压、电流、温度等)和电池内部状态(内部阻抗、荷电状态等)之间的关系，确定电池等效模型准确的参数，为精准的估计电池SOC提供重要基础。电池模型通过增加阶数对电池内部进行更加详细的描述，使得电池的模型更加精确，但这也会导致电池模型的复杂程度增加，对模型的参数辨识难度成倍增加，综合考虑采用二阶等效模型对电池进行研究。其等效电路模型如图2所示。

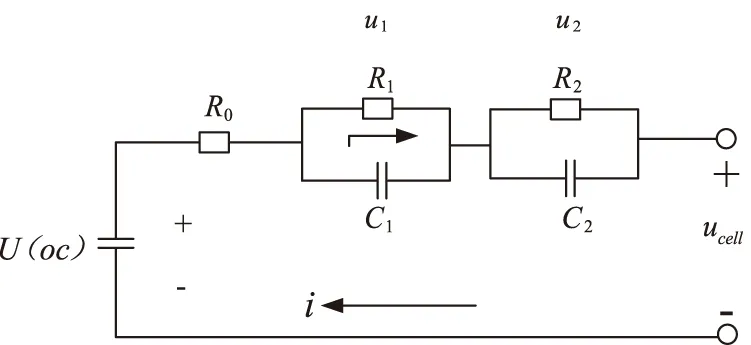
图2 单液流锌镍电池等效电路模型

其中U(OC)为开路电压，R0为欧姆内阻，R1和C1分别为电池内部电化学反应过程中产生的电化学极化电阻和电化学极化电容，R2和C2为电池充放电过程中化学反应导致电解液浓度变化产生的浓差极化电阻和浓度差极化电容，i为充放电电流，u1和u2分别为电流流过RC元件产生的电化学极化电压和浓度差极化电压，ucell为电池端电压。

根据基尔霍夫定律，可得

i=C1du/dt+u1/R1

(3)

i=C2du/dt+u2/R1

(4)

ucell=U(oc)-u1-u2-R0i

(5)

将上述式子离散化处理，可得

u1(k)=u1(k-1)ea+i(k-1)R1(1-ea)

(6)

u2(k)=u2(k-1)eb+i(k-1)R2(1-eb)

(7)

ucell(k)=Uoc(k)-u1(k)-u2(k)-Roi(k)

(8)

其中，a=-T/R1C1，a=-T/R2C2.T为采样周期，k为放电时间。

状态方程

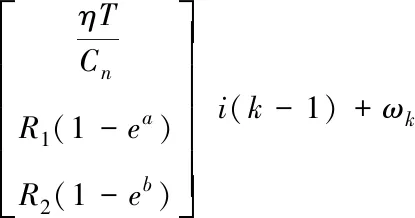
(9)

观察方程

ucell，k=f(SOC(k))-U1(k)-U2(k)-ikR0+vk

(10)

其中，ωk和vk分别表示过程噪声和测量噪声，后同，f(SOC(k))是开路电压关于SOC的函数。

2.3 单液流锌镍电池模型参数识别

测试采用的充放电检测设备为新威CT-3004-5V200A-NTFA，先将电池充满，再以0.5C进行恒定电流进行脉冲放电，每次放电量为0.7Ah，并将静置循环过程的周期设置为30分钟，将采集的数据与式(11)和(12)结合，利用Matlab的cftool工具拟合得到R0、R1、R2、C1、C2等重要参数，参数表如表1所示。

电池放电出现的突变电压Δu由R0产生，所以有

Δu=R0i

(11)

电池静置的时候，端电压幅值变化是u1和u2改变引起的，所以这个过程端电压变化表达式为

ucell=U(oc)+iR1e-t/(R1C1)+iR2e-t/(R2C2)

由表1中看出，实验过程中，各个参数都是动态变化的，且幅值较大，其中R0、R1和R2分别随着SOC的减小由7.91mΩ、3.40mΩ和2.59mΩ逐渐升高至10.11mΩ、5.41mΩ和3.63mΩ，C1和C2分别随着SOC减小由76.71KF、8.40KF逐渐降低至33.17KF、3.44KF，总体来看电池内部阻值在放电过程中逐渐增大，内部电容在放电过程中逐渐减小。

在进行脉冲充放电实验时，记录SOC从0到1变化过程中相对应OVC的值，然后通过使用Matlab的cftool工具对实验所记录的数据进行拟合，得到电池充放电的OVC-SOC拟合曲线图3，电池充放电的开路电压解析表达式为

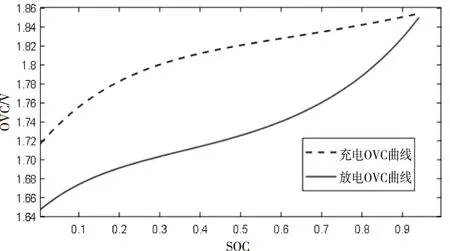
图3 单液流锌镍电池充放电OVC-SOC关系拟合曲线

1)开路电压充电过程表达式

f(SOC)=0.1552×SOC5-0.6487×SOC4+1.147×SOC3-1.01×SOC2+0.5022×SOC+1.714

(13)

2)开路电压放电过程表达式

f(SOC)=0.4846×SOC5-1.185×SOC4+1.488×SOC3-0.9043×SOC2+0.3574×SOC+1.646

(14)

3 无迹卡尔曼滤波(UFK)算法估计电池SOC

EKF算法是通过将非线性问题线性化来进行估计，但这个过程中由于忽略了高阶项，增大了计算误差，且运算量较大。而UKF算法时通过对产生的Sigma点进行UT变化，计算过程均是非线性的，可以避免线性化过程中产生的误差，提高估算的准确性，并且没有使用泰勒展开线性化处理，也大大的减小了计算量。单液流锌镍电池的系统状态方程(9)和测量方程(10)用式(15)来表示，其中系统状态为xk，测量方程为yk。

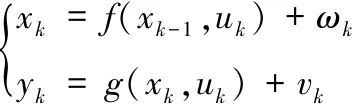
(15)

其中，uk是系统的输入变量；f和g分别表示非线性的系统模型和测量模型。

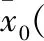
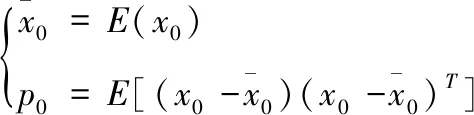
(16)

2)计算sigma点

(17)

其中n为状态变量的个数，对于单体电池，取值为2；λ为一个比例系数，其表达式为：

λ=a2(n+h)-n

(18)

其中a为一个正数，通常取值为1；h为缩放参数，通常取值为0。

3)确定加权系数

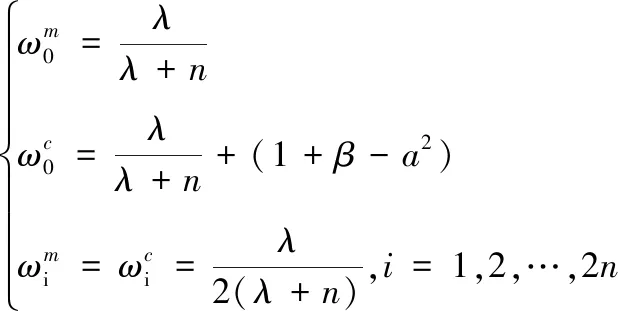
(19)

其中，ωm，ωc分别为权重因子；β对于高斯白噪声系统一般取2。

4)时间更新

xi，k|k-1=f(xi，k-1，uk)，i=0，1，…，2n

(20)

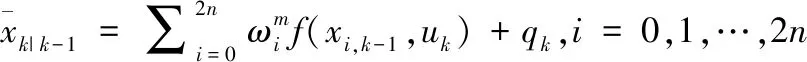
(21)

其中，qk为过程噪声均值。

+Qk，i=0，1，…，2n

(22)

其中，Qk为过程噪声协方差。

5)测量更新

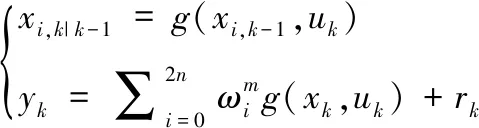
(23)

其中，rk为测量噪声均值

(24)

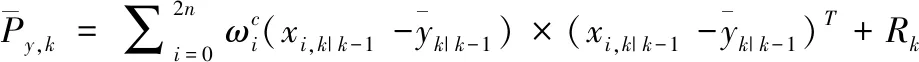
(25)

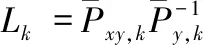
(26)

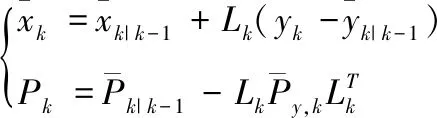
(27)

其中，Rk为测量噪声协方差。

4 实验验证分析

为了验证UKF估计单液流锌镍电池荷电状态的性能，取SOC=0.95，进行恒流脉冲放电实验，放电电流设置为14A，采样周期取T=1s，以安时法估算的结果作为参考(当准确知道SOC的初值，电池的SOC可以用安时积分法计算所得的结果来表示)，分别使用扩展卡尔曼滤波算法和无迹卡尔曼滤波算法对电池的SOC进行估计，结果如图4所示。

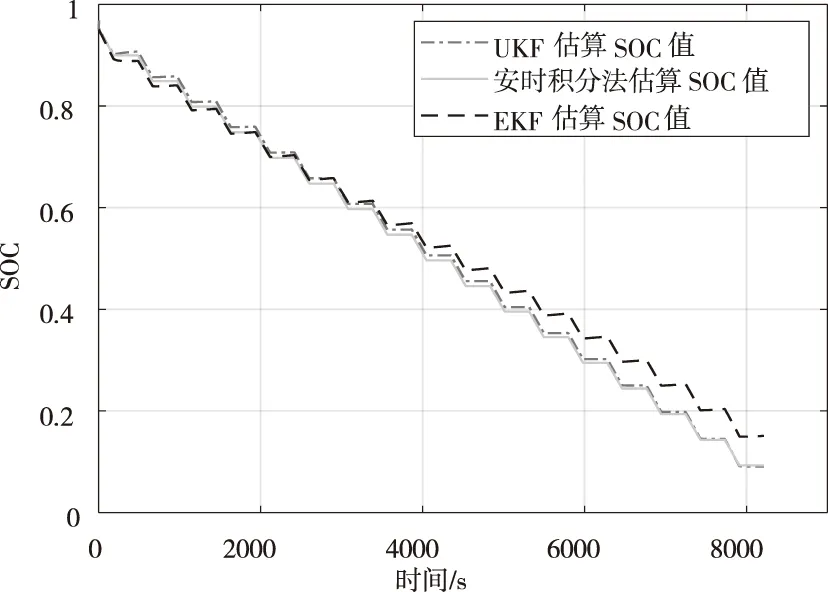
图4 SOC初始值为0.95时估算结果

EKF和UKF估算值与参考值误差比较得到图5和图6。

从图4中可发现EKF算法在前4000s都有较好的跟随变化，但4000s以后误差逐渐增大，图5中可以明显的发现EKF算法的误差是随时间不断累积增加的，随着时间到达放电末期出现最大误差为6.05%；对于UKF算法，可以从图4中看出UKF估计的SOC紧跟参考的SOC曲线变化，通过图6的误差比较可以发现UKF算法最大误差出现在放电初期值为1.82%，在10s以后误差保持在1.09%以内，且误差波动的幅值也较小，说明对与单体单液流锌镍电池，UKF算法估计SOC的精度高于EKF算法。

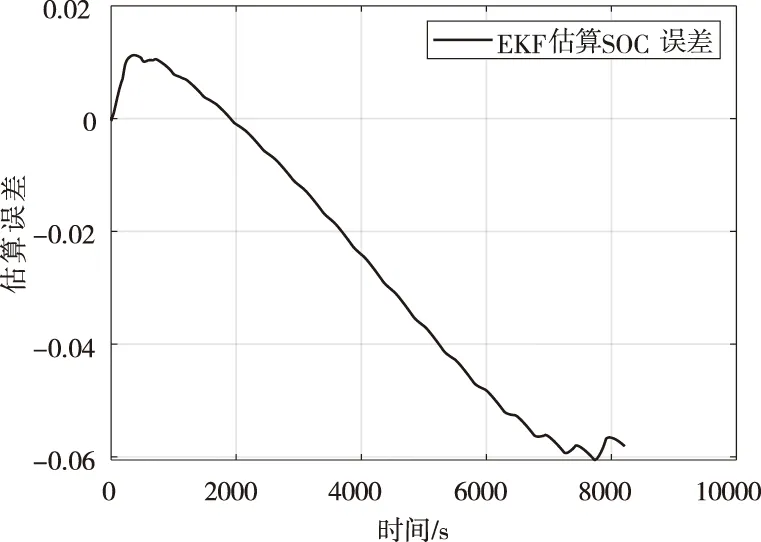
图5 EKF算法估算误差

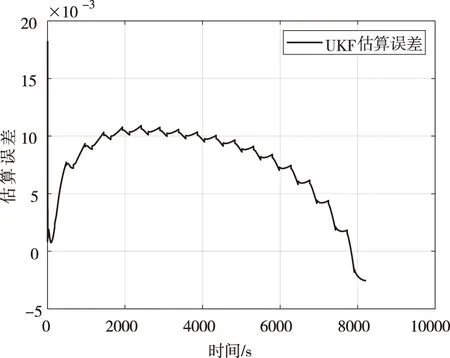
图6 UKF算法估算误差

5 结语

本文提出一种针对单液流锌镍电池荷电状态的UKF估计算法，从模型参数辨识可以发现电池内部参数随SOC变化而改变，但根据仿真结果可以发现UKF算法仍然具有较高的估算精度，主要是由于UKF算法在计算工作中没有将状态变化线性化处理，从而避免线性化过程中忽略高阶项产生的误差，这样利用UKF算法对单液流锌镍电池荷电状态估计能满足精度要求。但在实际电池运行中，电池在不同工况下的噪声(主要为过程噪声和测量噪声)是不断变化的，UKF算法初始化后噪声矩阵无法进行实时调整，这将会导致估算的精度降低，可以通过加入自适应控制的方法在工况改变的时候，及时对噪声更新，以期电池状态估计效果更好。