基于DSM湍流模型的气固圆湍撞击流模拟
2021-12-10耿察民任少君
耿察民,蒋 骏,任少君
(1.江苏方天电力技术有限公司,江苏 南京 211102;2.国网江苏省电力工程咨询有限公司,江苏 南京 210008;3.东南大学能源与环境学院,江苏 南京 210096)
1 引言
气固两相湍流射流普遍且大量地存在于各类自然界和工程应用相关的物理运动过程与化学反应过程中,其中煤粉锅炉气固多射流的燃烧一直是研究的热点,煤粉颗粒的扩散程度是影响锅炉传热效率和燃烧效率的重要因素之一。
近年来,众多学者采用了实验和模拟的方法来探索气固两相单射流的流动规律,这些研究多集中在固相对流场的调制[1-3]以及颗粒在流场中的弥散规律[4,5],并取得了一些成果。然而,对问题更为复杂的多射流中气固两相之间的相互作用以及对流场质量输运、动量输运、能量输运造成的影响的研究有限。同时,国内外学者也通过开展试验与模拟研究探索了单相对冲射流的流场[6-9],并对两相对冲射流中涉及对冲射流滞止点[10-12]、射流周期偏转震荡[13]、工业应用背景下的流场特征[14,15]等方面取得了一定的研究成果。然而,迄今为止有关气固两相多射流的两相相互作用机理研究的公开报道仍较少,有待进一步有针对性地开展研究。
轴对称对冲圆湍射流是对冲燃烧等对冲射流的基本流动形式,本文以轴对称对冲圆湍射流流动作为研究对象,对气相场采用大涡模拟方法,对固相采用离散相模型,并采用双向耦合的方法考虑固相与气相场的相互作用,研究对冲圆湍射流流场内颗粒的扩散规律以及多射流的湍流变化规律。
2 基本控制方程
2.1 气相改进的LES湍流模型
大涡模拟的基本思想在于把湍流的瞬时运动通过滤波的方法分解为大尺度运动和小尺度运动两部分[17],大尺度运动对平均流动其主要作用,包含湍流大部分的传质、传热及能量输运,而小尺度运动对平均流动影响较小,主要起粘性耗散的作用。过滤后的湍流大尺度运动量可直接数值求解,而小尺度湍流运动对大尺度运动量的影响则通过构建模型来模拟。本文基于Smagorinsky-Lily大涡模型[18],采用DSM(Dynamic-Smagorinsky model)大涡模型,即对传统Smagorinsky大涡模型的控制方程进行二次过滤,从而实现对气固圆湍对撞流的湍流流动的三维数理建模。一次过滤用上标 ~表示,二次过滤用上标~表示,时均运动量用上标^表示,因此过滤后的湍流质量守恒的连续性方程和动量守恒方程如下
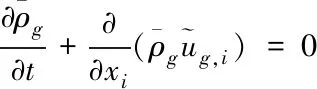
(1)
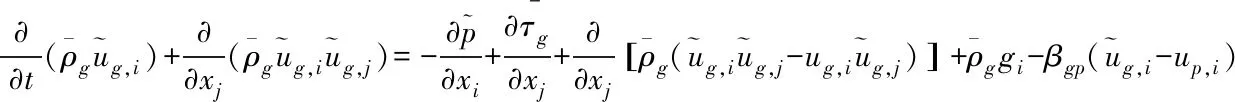
(2)
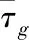
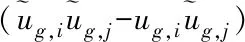

同样引入涡黏度模型进行过滤,则二次过滤的应力张量可表示为:
一次过滤

(3)
二次过滤
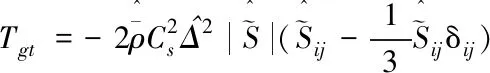
(4)
其中,Cs通过Lily提出的最小二乘法获得其收缩解[20-21]。
2.2 颗粒运动方程
本文在模拟固相颗粒场时,作了以下假设:固体颗粒视作球形,且颗粒粒径统一分布。由于固体颗粒的密度远远大于流体密度,因此颗粒所受的合力仅考虑重力和曳力,忽略了马格努斯旋转提升力、萨夫曼剪切提升力、压力梯度力、热作用力、虚拟质量力、范德华力、巴塞特力、浮力等[22-24]。因此,仅考虑气固曳力和重力的颗粒运动方程可写为

(5)
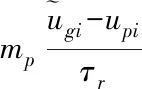
2.3 四向耦合的颗粒碰撞模型
本文基于直接模拟蒙特卡洛方法(DSMC)来计算气固四角切向湍射流中的颗粒碰撞,其基本思想为用少量的样本颗粒代替众多真实颗粒,通过统计样本颗粒的运动状态实现对真实颗粒运动的模拟[26]。即,在DSMC方法中,判断一个颗粒与另一个颗粒碰撞主要由碰撞概率决定,而不是由确定性方法颗粒的轨道决定。本文中的颗粒数量多,颗粒粒径较小且均匀分布,因此采用在拉格朗日轨道的基础上建立的Tanaka模型[27],其颗粒碰撞概率为

(6)
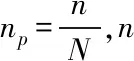
基于修正Nanbu算法来计算真实流场中的颗粒碰撞,每个样本的颗粒碰撞概率分布遵循泊松分布,因此O’Rourke给出流场中的颗粒碰撞概率为
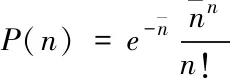
(7)
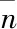
3 边界条件及求解方法
选取底面直径为300mm,长度为600mm的圆柱形区域作为射流流场求解区域,左右设有两直径为20mm的同轴圆湍射流入口。气相为空气,入口为速度入口,初始速度15m/s,雷诺数为11976,出口为压力出口Pout=-100Pa,墙壁为无滑移边界。对离散相设置为,每个时间步长喷入流场380个颗粒,其中气相时间步长与颗粒相步长一致,均设置为0.00001s,每一次气相场的计算完成后均计算一次颗粒相的迭代。颗粒密度为2000kg/m3,粒径分别为1μm、15μm和50μm,对应St数为0.005、1和12.5。
本文所构建三维非稳态气固圆湍对撞流三维数学模型的求解依托于商业软件ANSYS Fluent完成,其求解过程通过PC-SIMPLE(Phase Coupled Semi-Implicit Method for Pressure Linked Equations)方法进行压力-速度耦合的计算处理。气相时间步长与颗粒相步长一致,均设置为0.00001s,每一次气相场的计算完成后均计算一次颗粒相的迭代。三维非稳态求解结果的收敛标准设置为所有相关控制方程残差绝对值小于0.001。
4 结果和讨论
4.1 气相时均流场模拟结果
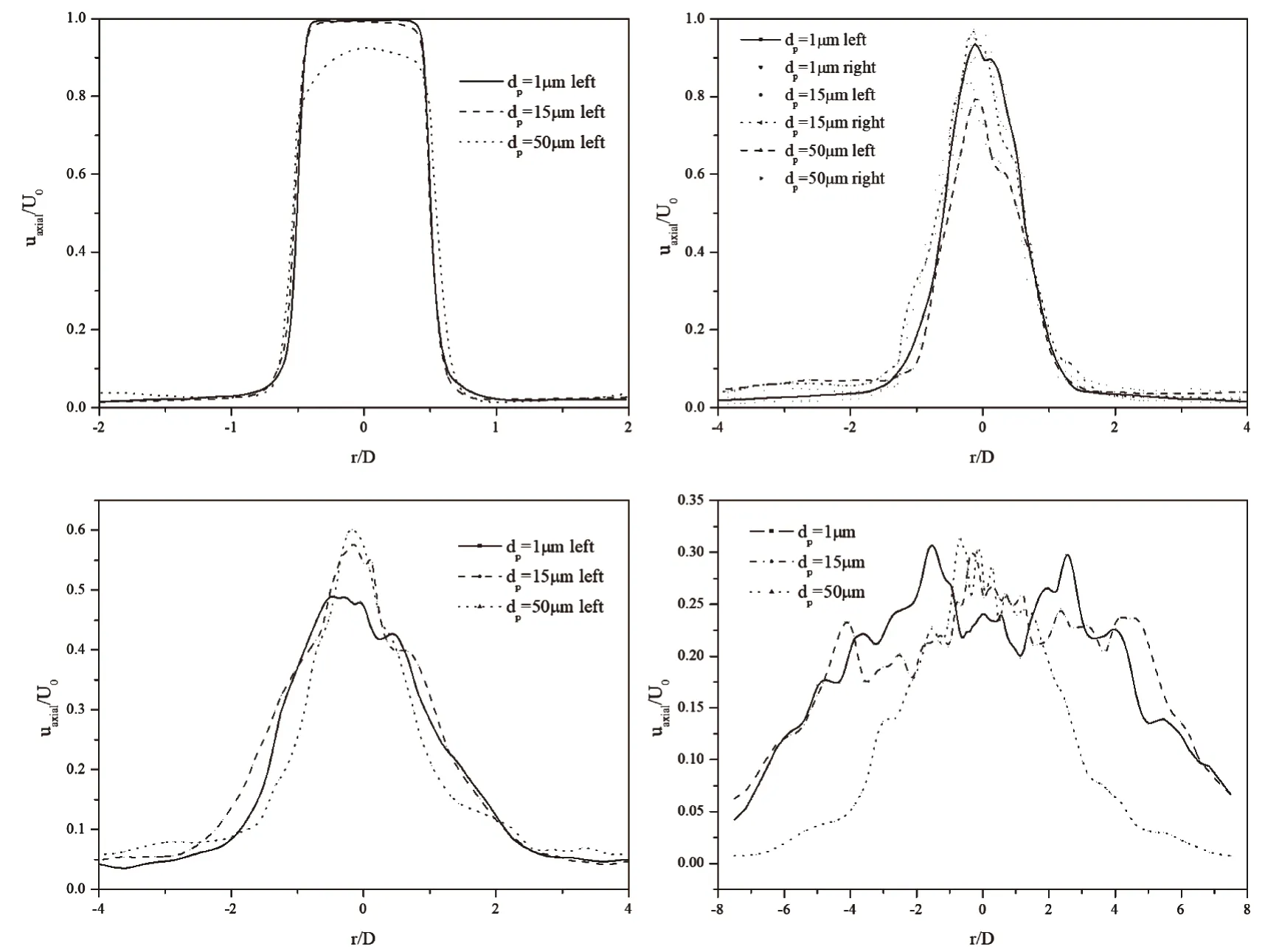
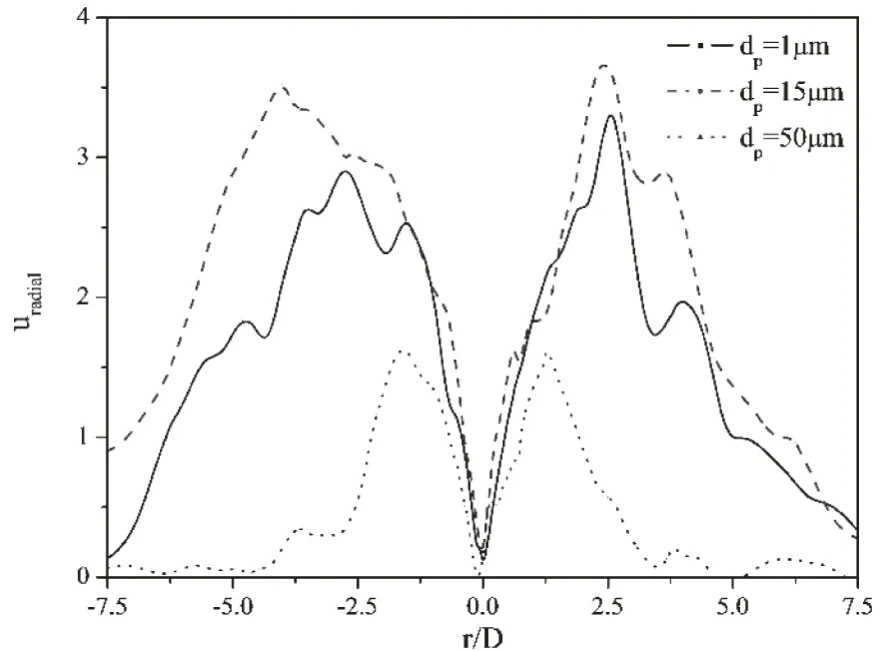
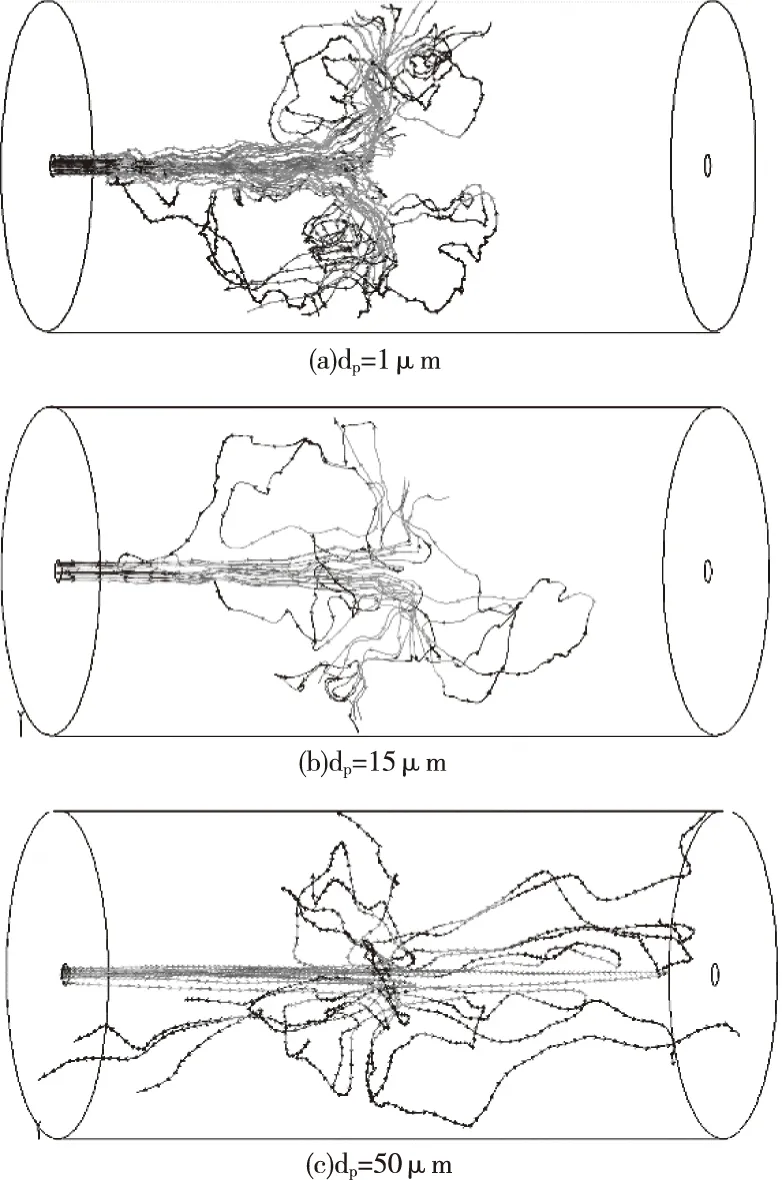
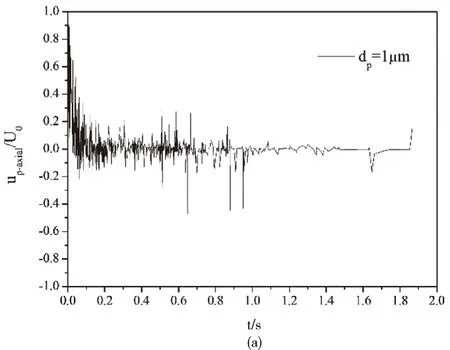
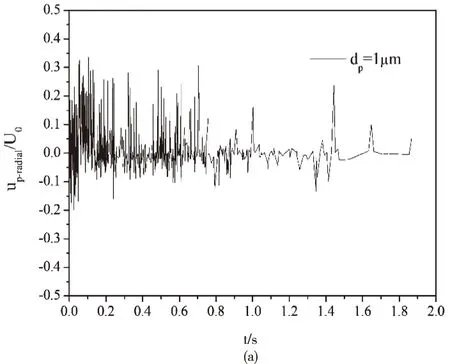
图1为添加颗粒后的气相场沿中轴线的时均流向速度分布。L为距离射流入口的距离,沿中轴线方向将流场划分为三部分:近喷嘴区(0 图1 气相场沿中轴线的时均流向速度分布 图2 气相场沿中轴线的时均流向速度分布 由此可见,在对冲射流中,Stokes数较大的颗粒在入口处对气相的耗散最大,Stokes数较小的颗粒在远喷口区对气相场的耗散最大,Stokes数在1的数量级的颗粒在碰撞区域对气相场的耗散最大。 图3为对冲中心面气相场时均径向速度的径向分布。显然可见,在对冲碰撞面,气流向出口流动,气速达到最大值后逐渐下降。添加粒径为15μm的颗粒使径向速度达到最大值且最大值出现在距离中心最远的位置;添加粒径为50μm的颗粒使得径向速度耗散最大,且很快降到0,甚至出现负值;同样的,1μm的颗粒也存在对径向气速的耗散。由此可见,在对冲中心面上,Stokes数较大的颗粒使得气相刚性增强,气相扩散减小,而Stokes数为1数量级的颗粒对气相的耗散较小,并在一定程度上减小了气相的横向扩散。 图3 对冲中心面气相场时均径向速度的径向分布 轴对称气固两相圆湍射流具有高度对称性,因此下文颗粒分析主要针对左端入射口的颗粒信息进行分析。 4.2.1 颗粒运动轨迹 图4是不同Stokes数的颗粒在流场中的运动轨迹。可见,Stokes数较小的颗粒轨迹大多呈现绕小圈的“小涡”,表明小颗粒跟随性较好紧随气相流动的变化;Stokes数在1数量级的颗粒轨迹大多呈现绕大圈的“大涡”,这表明中等大小颗粒主要受到气相涡的离心力作用;Stokes数较大的颗粒受到气相场的影响较小,部分大颗粒保持自身惯性向前做减速运动,触到壁面后反向加速,部分颗粒由于受到对面来流颗粒的撞击,直接改变运动方向,但颗粒大多保持直线运动,这表明气固射流中大颗粒本身的惯性起到主要作用,气相场对其影响较小。 图4 不同Stokes数的颗粒在流场中的运动轨迹 由于射流的对冲碰撞,气相在对冲中心形成滞止点,颗粒易在滞止点积聚。Stokes数较小的颗粒在堆积后的颗粒又受到向出口扩散的气相涡的影响,颗粒进入涡的内部并向出口扩散;Stokes数在1的数量级的颗粒又受到向出口扩散的气相涡离心力的影响并向出口扩散;Stokes数较大的颗粒没有随着气相涡向出口扩散。可见在对冲湍流射流中,颗粒的运动仍符合单射流中颗粒的运动规律[13]:数较小的颗粒在气固射流场中跟随性较好,颗粒容易被流体卷吸,颗粒多分布在大涡结构内部,扩散率小,在流场中的分布较为均匀;Stokes数在1的数量级的颗粒在气固射流场中受到大涡结构旋转离心力的影响较大,颗粒多分布在涡结构的外围,扩散率较大,且分布不均;Stokes数较大的颗粒自身惯性较大,对冲碰撞使得颗粒在全场分布且不均。 4.2.2 颗粒速度分布规律 图5和图6分别表示左端入射口气固射流中某一颗粒瞬时轴向速度与瞬时径向速度随时间分布规律。可见,Stokes数较小的颗粒在对冲射流流场中容易达到稳定,Stokes数在1的数量级的颗粒由于受到离心力的作用,径向速度不易达到稳定,Stokes数较大的颗粒自身惯性较大,难以在流场中达到相对稳定。 图5 不同粒径的颗粒瞬时轴向速度的时间分布 图6 不同粒径的颗粒瞬时径向速度的时间分布 本文对气固两相轴对称对冲圆湍射流采用大涡模拟模拟对气相场进行模拟,采用离散相模型对离散颗粒进行模拟,研究了不同粒径下对冲射流气相场的分布以及颗粒弥散规律。结果表明:在对冲中心面上,Stokes数较大的颗粒使得气相刚性增强,气相扩散减小,Stokes数为1数量级的颗粒对气相的耗散较小,Stokes数为1的颗粒一定程度上减小了气相的横向扩散。在对冲碰撞区域,射流的碰撞导致湍流强度增大,涡结构破碎,气相形成滞止点,颗粒多聚集在滞止点区域,Stokes数小于1的颗粒对气相横向扩散影响较小,颗粒又会随着涡结构向出口扩散而扩散,Stokes数较大的颗粒惯性大,不受气相场影响,颗粒聚集在滞止点区域。 符号说明: ρ 密度 u 速度 p 下标,颗粒相 g 下标,气相 μ 动力粘度 ν 运动粘度 κg气相的湍动能 g 重力加速度矢量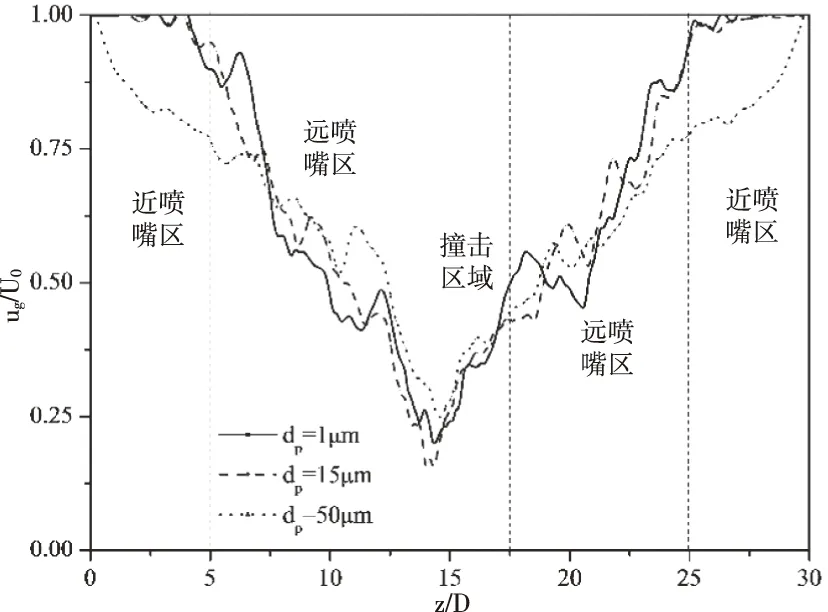
4.2 颗粒的扩散特性
5 结论
