Delta并联清洗机构轨迹跟踪控制方法研究
2021-12-10董慧芬宋金海
董慧芬,王 渗,宋金海
(中国民航大学电子信息与自动化学院,天津 300300)
1 引言
机场嵌入式助航灯具由于外界环境污染,会造成其发光强度降低,危及航空安全,故机场需要定期进行人工清洗。实现灯具自动清洗是提高清洗效率,降低机场运行成本的重要手段。目前为止,国内跑道助航灯具大多采用人工清洗,清洗效率低,人工成本高是机场运营的痛点,而国外的自动化清洗设备价格高昂,绝大多数机场难以负担,在此背景下,渴望一款高效自主研发的机场跑道助航灯具清洗设备运用而生。本文首次提出一款Delta并联清洗机构,对机场跑道助航灯具进行自动清洗。并联清洗机构末端对准助航灯具发光口实现精确控制是实现自动清洗的关键,因此,本文重点研究Delta并联清洗机构末端的轨迹跟踪控制的问题。
1985年,Clavel博士发明了一类三自由度空间平移并联结构,即著名的Delta机械人[1]。Delta机器人克服了并联机构的很多缺点,有着精度高、刚度高、速度快和承载能力大等特点,因而被广泛应用。早期的并联清洗机构控制策略大多采用的是传统的PID控制,但其建立的运动学模型会存在一定的不确定性,原因归结于该机构本身系统复杂,输入输出变量多,是一个多参数耦合的非线性系统,在物理上就已经非常难获取相应的准确值,因此,传统的 PID 控制难以取得很好的控制效果。针对并联机构的控制和优化问题,已经有很多国内外学者做了研究。在文献[2]中,为一种直线类型Delta机构设计了一种神经网络控制器,并仿真验证了神经网络算法良好的时效性。2016年李丽丽等人采用PC作为上位机和ARM作为下位机的控制策略,建立了一个三自由度Delta高速机器人协调控制系统,具备了系统性能好,研发周期短,经济效益高等优点[3]。这种控制方法俨然已成为Delta机器人控制手段的新方向。模糊控制因其具备非线性控制和鲁棒性优良等特征,非常适合用来控制时变参数、非线性系统,使其控制手段简单,控制效果非常明显。兰州理工大学的陈艳娟进行了Delta机器人轨迹跟踪控制仿真研究[4]。卢兴国针对于轨迹跟踪控制问题,提出了模糊神经网络PID控制器提高稳定性[5]。哈尔冰工业大学的刘明等人提出一种自学习区间型模糊神经网络(SLIT2FNN)控制方案进行仿真,证明了所提出控制器的性能和鲁棒性[6]。Bionotes等人提出一种在对齐条件下的迭代学习控制器(ILC),用于并行Delta机器人的轨迹跟踪,得到位置和速度误差随着迭代次数的增加而减小,仿真验证该控制器的有效性[7]。很可惜他们都只停留在仿真阶段,没有具体的运用于实际且进行实验验证。
综述以上,提出模糊自适应PID控制器并运用于Delta并联清洗机构,仿真和实验验证了该控制器较传统PID控制器相比,不仅节省清洗时间,而且还提高了清洗效率。
2 并联清洗机构分析
自动清洗机构采用的四自由度Delta并联机器人,因其具有结构简单、承载能力强,动作快速,刚度大,精度高,又有良好的运动学和动力学特性等众多特点。四自由度Delta并联清洗机构主要由移动单元、清洗单元和并联机构单元三部分组成。清洗单元包括:空压机、粉末罐、电磁阀,高压软管,末端夹持机构,喷嘴等装置;并联机构单元包括:动平台、静平台、伺服驱动电机、限位开关、主动臂、从动臂、旋转轴、摄像头等。移动单元包括搭载的整个车体,方便灵活,可也以快速移动,清洗一排排跑道助航灯具。Delta并联机器人动平台携带清洗喷嘴定位到达助航灯具发光口,打开清洗开关进行自动清洗,对洗完后的灯具进行光效评估,判断是否需要优化清洗参数二次清洗。具体结构如图1所示。
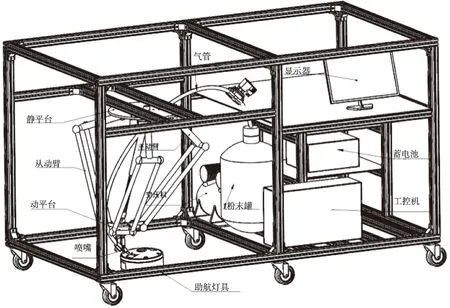
图1 四自由度Delta并联清洗机构
如图1所示,并联机构单元有两个平台:静平台和动平台。静平台一般与固定装置连接,是主要的承载装置,用来安装固定零件,舵机等主要部件;动平台主要是用来安装和固定末端控制器的机构,并且能够阻止末端执行器与机械臂的相对运动。舵机均匀分散安装在静平台的三个角上面。主动臂和从动臂将动平台和静平台连接起来,每个从动臂都由四个球铰和杆件组成的平行四边形闭环组成。工作时,舵机将动力传递给主动臂,主动臂通过球铰将动力传递给从动臂,从动臂最后将动力传递给动平台,来完成对末端执行器的控制。
Delta并联清洗机构采用单目视觉定位提取助航灯具发光口坐标,并输入目标点到并联机构单元进行运动学逆解,得到电机旋转角度,通知下位机实现自动清洗,对清洗结果进行光效评估。具体清洗控制流程如图2所示。
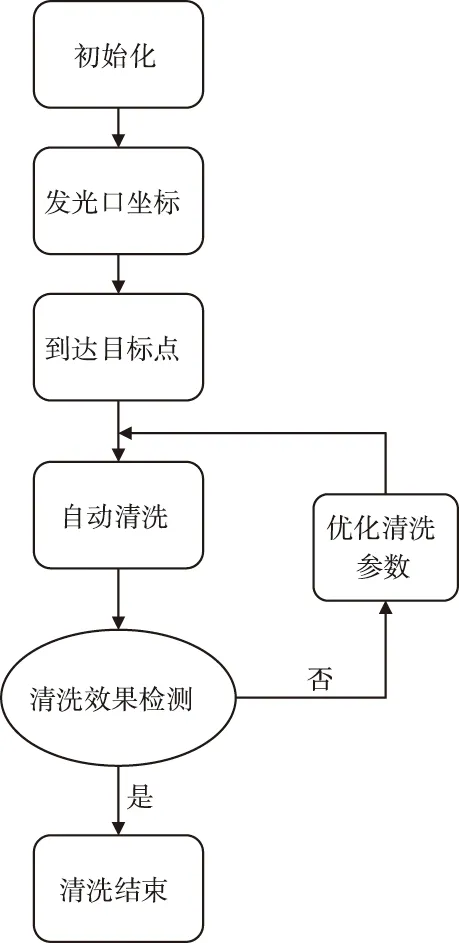
图2 清洗控制流程图
2.1 Delta并联清洗机构运动学正解
运动学正解就是在已知电机的输出角位移情况下,来求解清洗机构末端位姿输出的位置参数。并联机构正解求解过程相对于逆解的求解过程来说十分复杂,逆解大多数采用上述的矢量法进行求解,而对于正解的求解过程一般采用几何解析的算法来进行求解,韦岩等人[8]通过将并联机构进行简化建模,发现静平台和动平台始终平行,通过平移模型中的从动臂,从而将机构的正解求解问题转化为对一个已知所有边长及3个顶点坐标的三棱锥求解顶点坐标的问题。已知的三个顶点坐标为

(1)

2.2 Delta并联清洗机构运动学逆解
运动学逆解就是在已知目标位置的前提下,求解各舵机的输入和末端位姿输出的关系。运用空间几何学和矢量代数的方法建立了四自由度Delta并联清洗机构的简化模型,求解得到并联清洗机构位置的逆解方程[9]。清洗机构的静平台和动平台之间通过主动臂与从动臂相连接,工作时由舵机驱动主动臂运动,然后主动臂带动从动臂一起运动,最后从动臂控制末端动平台的运动状态。由上述分析可知,求解清洗机构逆解就是在已知动平台中心O′在静平台坐标系的坐标下,求解电机的旋转角度,即主动臂相对于静平台的角度。由此可得Delta并联机器人逆运动的位置解为

(2)
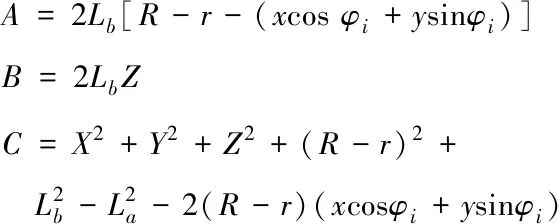
(3)
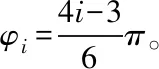
3 末端模糊PID轨迹跟踪控制器
模糊自适应PID控制器原理简单,使用方便,适应性强,灵活稳定。对于非线性和时变性较大的控制系统,在控制方面相较于传统的PID控制器,优点就显得更加突出。
3.1 模糊自适应PID控制器
需要定义输入、输出模糊集并且确定个数类别,参考经典PID的控制方法以及依据模糊PID控制器的控制规律,于此同时要兼顾控制精度,提高系统的响应特性[10],为此取出3个模糊集N(负),Z(零),P(正)。本文模糊控制集取
e,ec={N,Z,P}
(4)
输出的ΔKp,ΔKd,ΔKi也同样取3个模糊集
ΔKp,ΔKd,ΔKi={N,Z,P}
(5)
根据控制要求,确定输入输出变量的实际论域,对各个输入输出变量做如下划定
e,ec={-1,0,1}
(6)
ΔKp,ΔKd,ΔKi={-0.01,0,0.01}
(7)
应用模糊合成推理PID参数的整定算法。第k个采样时间的整定为

(8)
式中,Kp0,Ki0,Kd0为经典PID控制器的初始参数,具体的控制流程如图3所示。
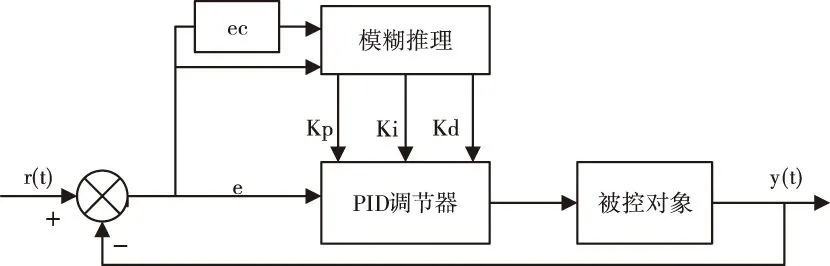
图3 模糊自适应PID控制系统
3.2 模糊规则的建立
针对Kp,Ki,Kd三个参数对系统输出特性的不同表现,建立了一套合适的关于e,ec,Kp,Ki,Kd的模糊规则推理表,具体如表1,表2所示。

表1 比例参数取值的模糊规则表

表2 积分参数取值模糊规则表
4 清洗机构末端跟踪控制建模
并联清洗机构末端的闭环控制系统框图如图4所示。

图4 闭环控制原理框图
4.1 清洗末端传统PID控制仿真模型
建立图5所示的闭环控制仿真模型[11],其中控制器选用PID控制器。位置采用PID控制,仿真时调整PID的参数。IK和FK依然是并联清洗机构逆解和正解的求解程序,generator为电机的封装模块,这里将负载从模块中独立出来,可以方便在仿真时随时改变给定的负载。将正解输出作为位置反馈,构成闭环。
4.2 清洗末端模糊PID控制仿真模型
将图5中的PID环节替换为Fuzzy PID模块,其它模块与环节保持不变,模糊PID可以PID的参数进行自整定,图中的Fuzzy PID模块为封装模块,它的子系统如图6所示。
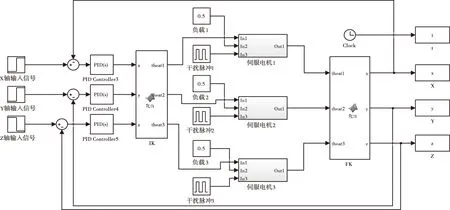
图5 传统PID仿真模型

图6 Fuzzy PID子系统
5 仿真结果分析
仿真时选择一组目标值,输入坐标选择为(150,50,-100)的阶跃信号,即X的输入为150mm,Y的输入为50mm,Z的输入为-100mm。仿真X,Y,Z的输出的曲线如图7所示,其中图(a)为X的输出曲线,图(b)为Y的输出曲线,图(c)为Z的输出曲线。为方便与PID输出的曲线做比较,将PID输出和模糊自适应PID输出的曲线在同一个界面显示出来。其中虚线型曲线是模糊自适应PID控制时的位置输出,实线型曲线是PID控制时的位置输出。
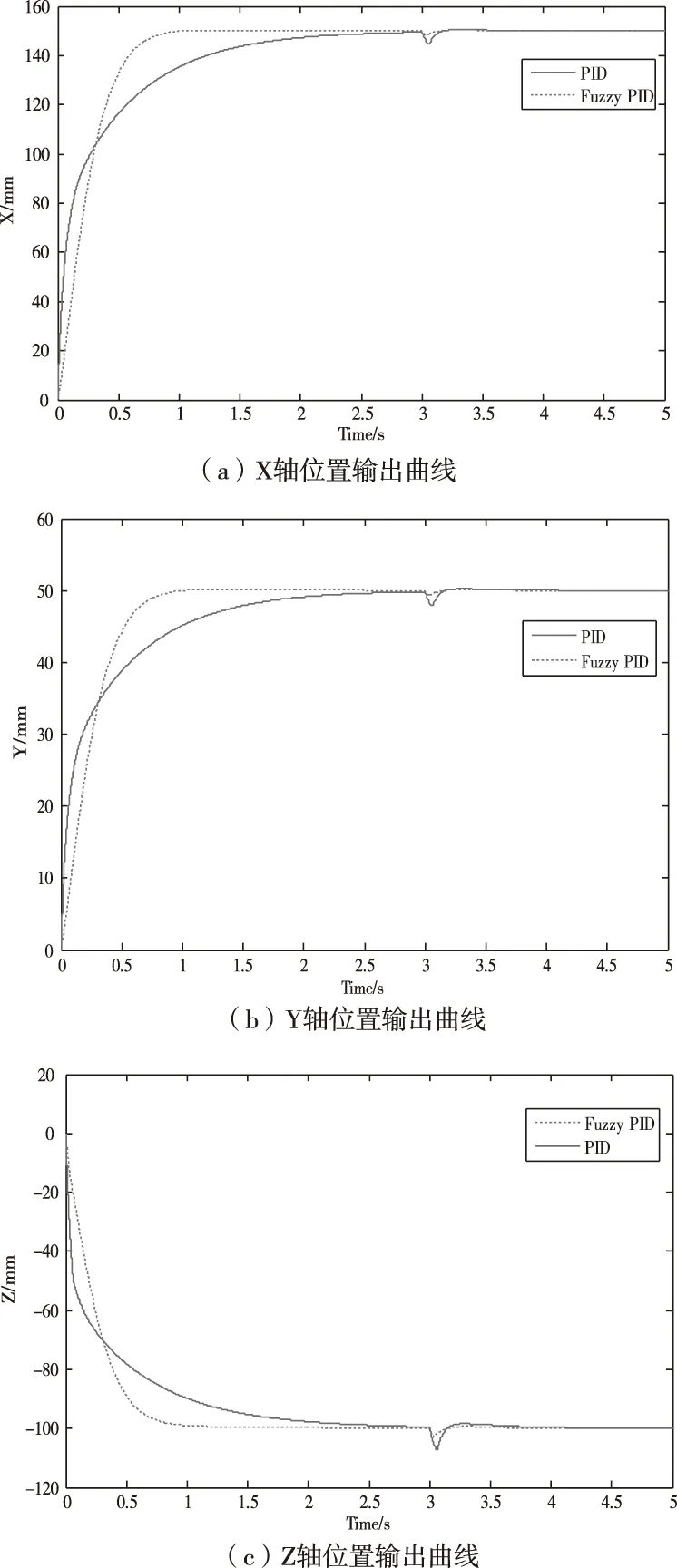
图7 阶跃信号位置输出对比曲线
从上述三图可以看出,图(a)为X位置输出曲线,采用模糊自适应PID控制,从曲线中可以看出在仿真开始初期的0.8s时间内,曲线变化很快,在1s左右的时候达到了稳定,没有超调量。采用PID控制设定好参数后,在2.5s左右的时间才达到稳定,此时X轴稳定在了148mm的位置,稳态误差为2mm。曲线图(b)为位置输出Y的曲线,采用模糊自适应PID控制,从曲线中可以看出在仿真开始初期的0.8s时间内,曲线变化很快,并且变化趋势比较平缓。在1s左右的时候达到了稳定,此时X轴稳定在了150mm的位置。而采用PID控制设定好参数后,在2.5s左右的时间才达到稳定,此时Y轴稳定在了49mm的位置,稳态误差为1mm。曲线图(c)为位置输出Z的曲线,采用模糊自适应PID控制,从曲线中可以看出在仿真开始初期的0.7s时间内,曲线变化很快,在0.8s左右的时候达到了稳定,此时Z轴稳定在了-100mm的位置。而采用PID控制设定好参数后,在2.7s左右的时间才达到稳定,此时Z轴稳定在了-99mm的位置,存在1mm的误差。
仿真结果表明,模糊自适应PID与传统PID闭环控制相比提高了响应的速度和精度,可以很好地满足清洗要求,有效节省了助航灯具的清洗时间,降低清洗成本。Delta并联清洗机构采用模糊PID闭环控制使系统实现对目标位置的快速准确跟踪,可以看出该算法是高效可行的。
6 实验结果与分析
6.1 阶跃信号的实验结果分析
选择与仿真相同的目标点进行实验,即(150,50,-150)的阶跃信号。X,Y,Z轴的实验结果如图8所示,其中图(a)为X的输出曲线,图(b)为Y的输出曲线,图(c)为Z的输出曲线。PID输出和模糊自适应PID输出的曲线显示在同一界面进行比较。
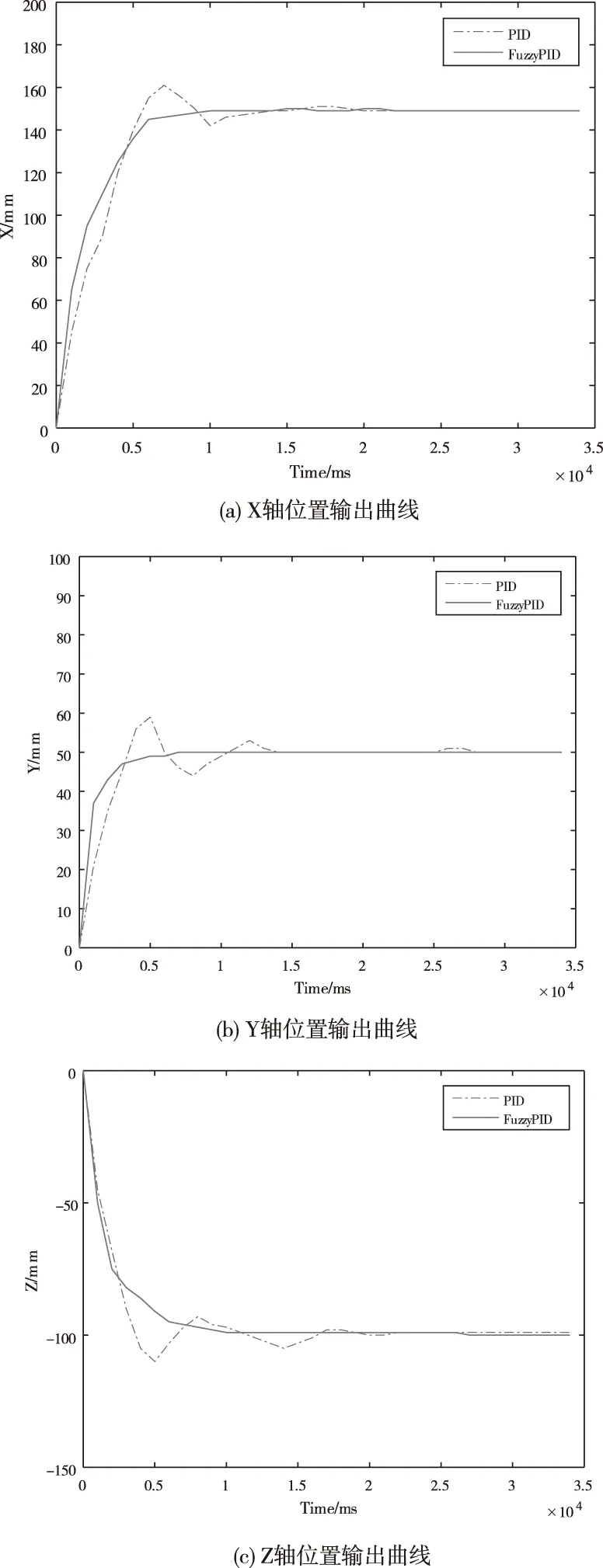
图8 阶跃信号实验输出对比曲线
从上述三图可以看出,实际控制当中,传统PID控制存在超调。X轴位置输出曲线,采用模糊自适应PID控制在0.9s达到了稳定,没有超调量。采用PID控制在0.7s有较大超调,2.3s后稳定在148mm的位置,稳态误差为2mm。Y轴位置输出曲线,采用模糊自适应PID控制在0.8s达到了稳定,没有超调量,稳定在50mm位置。采用PID控制在0.4s有较大超调,达到了60mm,1.7s后稳定在51mm的位置,稳态误差为1mm。Z轴位置输出曲线,采用模糊自适应PID控制在1s达到了稳定,没有超调量。采用PID控制在0.5s有较大超调,2.3s后稳定在-98mm的位置,稳态误差为2mm。
实验结果可以看出,并联清洗机构试验过程当中,由于机械安装等原因,PID控制会不约而同的产生超调,控制响应度和精确度较差。相比之下,模糊自适应PID控制算法优越性更强,在该模型运用当中的误差小,非常适合用在并联清洗机构当中。
6.2 轨迹跟踪实验结果分析
在Delta并联清洗机构的清洗工作空间中,输入螺旋上升状的理想轨迹信号,为了尽可能看清楚轨迹跟踪的细节状态,特此截取观察2个周期的跟踪轨迹,观测对比模糊自适应PID控制算法和经典PID控制算法的轨迹跟踪情况。采用立体图使视觉效果更佳,并且将理想轨迹曲线,PID输出曲线和模糊自适应PID输出曲线同时显示在同一界面当中,如图9所示。

图9 三维立体轨迹跟踪曲线
单从上面三维立体轨迹跟踪曲线可以看出,Delta并联清洗机构的响应速度很快,模糊自适应PID控制和PID控制都可以在非常短的时间内完成追踪螺旋理想轨迹。可以发现,模糊自适应PID控制的跟踪能力比PID控制更强,响应曲线更加贴近理想跟踪信号,微小幅度的超调,后期跟踪过程当中也没有出现超调幅度大或者严重的跟踪现象。而PID控制在刚开始时候出现了微小的偏差,慢慢的到后期,偏差逐渐明显,并且越往后偏差越大,跟踪偏差与模糊自适应PID控制算法相比较而言偏大,整体跟踪效果和性能略显稍差一些。
实验结果分析可知,模糊自适应PID控制算法提高了清洗机构的响应速度和精度,相较于助航灯具发光口大小,控制误差非常小,在允许的范围内,可以满足清洗要求。特别是运用在Delta并联清洗机构上,在线整定PID参数,能够使系统较快地趋于稳定,实现对目标位置的快速准确跟踪,精度高并且动态性能好,节省清洗时间,提高清洗效率,降低了机场清洗成本。
7 结论
运用Delta并联清洗机构清洗机场跑道嵌入式助航灯具发光口过程中,针对Delta并联清洗机构动平台末端定位难,误差大,难以满足机场清洗要求等问题,因此建立了Delta清洗机构模型,设计模糊自适应PID控制器,输入阶跃信号到Delta并联清洗机构中进行仿真和实验,并且与传统PID控制器进行对比。仿真实验结果充分表明,Delta并联清洗机构采用模糊自适应PID控制算法,清洗机构的响应速度提升1.3s,清洗末端控制精度达到2mm,单个灯具发光口清洗时间减少至1.5s,满足机场清洗要求且降低了机场清洗成本。模糊PID控制算法运用于Delta并联清洗机构是高效可行的。
