地下水地源热泵单井回灌率计算方法探讨
2021-12-09孔凡杜王玉虎柳晓松尚飞龙
孔凡杜 王玉虎 柳晓松 尚飞龙
摘要:在浅层地热能调查过程中,地下水地源热泵单井回灌率的计算没有统一的标准,用常规方法计算的结果不准确,甚至出现大于100%的现象。本文以兰陵县乡村振兴浅层地温能调查评价项目中L1号孔抽水回灌试验为例,对科学计算地下水地源热泵单井回灌率的方法和过程进行探讨,采用图解法和曲率法判断抽水试验曲线类型,利用最小二乘法和图解法计算抽水试验曲线方程,再根据曲线方程推算井孔在降深等于回灌试验最大升程的出水量,从而计算出单井回灌率。该计算方法科学、合理,计算过程简单、易操作,可作为浅层地热能调查和地下水地源热泵勘查、设计过程中资料整理的参考。
关键词:地下水地源热泵;单井回灌率
基金项目:山东省自然资源厅,兰陵县乡村振兴浅层地温能调查评价,鲁自然资函〔2019〕902号。
浅层地热能是从地表至地下200m深度范围内,储存于水体、土体、岩石中的温度低于25℃,采用热泵技术可提取用于建筑物供热或制冷等的地热能,这类低温热源可以大大地降低传统供暖与制冷的能耗,节约成本,具有较强的开发潜力,是一种绿色能源[1]。地下水含水层的回灌能力直接影响地下水地源热泵工程中回灌井的数量,从而影响地下水地源热泵工程建设和运行的成本,是浅层地热能调查评价工作的重要调查内容[2-4]。单井回灌率是表征地下水含水层的回灌能力的重要参数。
1.常规计算方法
作为表征地下水含水层回灌能力的参数,单井回灌率即为单井的回灌量与出水量的比值,一般情况下不同降深(或升程)单井的出水量(或回灌量)不同[5],因此单井回灌率采用单井单位升程的回灌量(单位回灌量)与单井单位降深的出水量(单位出水量)的比值进行计算(见公式(1))。
X=q灌/q出公式(1)
其中:X——单井回灌率,单位%;
q灌——单位回灌量,q灌=Q灌/S灌,单位L/(s.m);
q出——单位出灌量,q出=Q出/S出,单位L/(s.m)。
通常采用回灌试验最大升程的回灌量除以最大升程计算单位回灌量,采用抽水试验最大降深的出水量除以最大降深计算单位出水量。
下面以2019年开展的兰陵县乡村振兴浅层地温能调查评价项目中L1号孔抽水、回灌试验(见表1)为例进行探讨。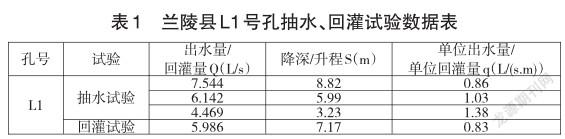
L1号孔于2019年11月19日至2019年11月22日开展了抽水和回灌试验,其中抽水试验进行了3次降深,抽水延续时间41.5h,最大降深8.82m,对应的单位出水量0.86L/(s.m);回灌试验进行了1次升程,回灌延续时间50h,最大升程7.17m,对应的单位回灌量0.83L/(s.m)。根据常规方法进行计算,L1号孔单井回灌率为96.5%。
2.存在问题分析
从表1中看出,抽水试验过程中不同降深时计算的单位出水量是不同的,计算的单位出水量在降深最低时最大,降深最大时最小,单位出水量随降深的增大而减小。
由于受到地下水位埋深的影响,回灌试验最大水位升程是一定的,从而造成单位回灌量是一定的;对于富水性强的含水层,受到回灌设备能力的影响,最大回灌量及最大水位升程是一定的,从而造成单位回灌量是一定的。根据公式1可知,单位回灌量位于分子位置,单位出水量位于分母位置。其中分子不变,分母是可变的,当抽水试验最大降深较小时,单位出水量较大,相应的单井回灌率较小;当抽水试验最大降深较大时,单位出水量较小,相应的单井回灌率较大,甚至出现超过100%的情况[6],这是不符合常识的。因此,常规方法计算单井回灌率是不合理的,不合理因素的关键是计算单位出水量时降深的选取。
3.計算方法探讨
3.1计算思路
根据以上存在问题的分析,要合理计算单井回灌率,就不能采用抽水试验最大降深时的单位出水量,而必须在抽水试验降深与回灌试验升程一致的情况下进行,而在实际试验过程中很难满足这样的条件,因此,就必须通过相关计算使得二者一致。
具体计算思路:①利用图解法或曲度法判断抽水试验曲线类型;②利用最小二乘法或图解法计算抽水试验曲线线性方程;③根据计算出的线性方程,计算出在与回灌试验最大升程相等的降深时的出水量;④计算出与回灌试验最大升程相等的降深时的单位出水量;⑤采用公式(1)计算出单井回灌率。
由于计算过程中计算出水量的降深与计算回灌量的升程相等,公式(1)可简化为:
X=Q灌/Q出推公式(2)
其中:Q出推——与回灌试验最大升程相等的降深时的出水量。
因此,以上计算思路可简化为:①利用图解法或曲度法判断抽水试验曲线类型;②利用最小二乘法或图解法计算抽水试验曲线线性方程;③根据计算出的线性方程,计算出在与回灌试验最大升程相等降深时的出水量;④采用公式(2)计算出单井回灌率。
3.2计算过程
下面我们还是以2019年开展的兰陵县乡村振兴浅层地温能调查评价项目中L1号孔抽水、回灌试验的数据为例进行计算。
3.2.1曲线类型判断
我们知道抽水试验Q-S曲线有直线型、抛物线型、幂函数曲线型、对数曲线型等4种类型[7-8]。在进行相应的变换后,这4种曲线都可以变为Q-S、S0-Q、lgQ-lgS、Q-lgS的线性方程。
直线型:Q=qS(公式(3))(q为待定系数);
抛物线型:S0=a+bQ(公式(4))(S0=S/Q,a、b为待定系数);
幂函数曲线型:lgQ=lgn+lgS/m(公式(5))(n、m为待定系数);
对数曲线型:Q=a+blgS(公式(6))(a、b为待定系数)。
判断抽水曲线类型一般有两种方法,即图解法和曲度法。
(1)图解法。对于有3次以上(含3次)降深的抽水试验(如L1号孔抽水试验)一般采用EXCEL图解法进行判断较为简便快捷,而对于只有2次降深的抽水试验则不可用。
先计算L1抽水试验的S0(S/Q)、lgQ、lgS(见表2),在将表2内容输入内容输入到EXCEL表格中,然后分别按Q=f(S)、S0=f(Q)、lgQ=f(lgS)和Q=f(lgS)四种曲线绘制离散点。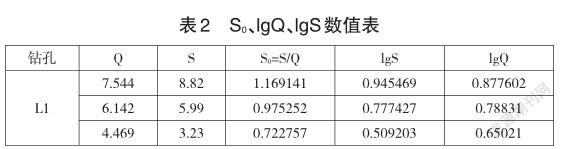
对Q=f(S)中的离散点添加多项式趋势线(拟合曲线),可以看出,Q=f(S)是曲线而不是直线,说明直线型可以排除,方程类型应为其他三种类型中的一种。
分别对另外三种曲线图中的离散点添加线性趋势线,并显示线性公式及R平方值(即判定系数),根据拟合结果可以看出,三种曲线线性趋势线的R平方值分别为0.9995、0.9999、0.9937,见图1。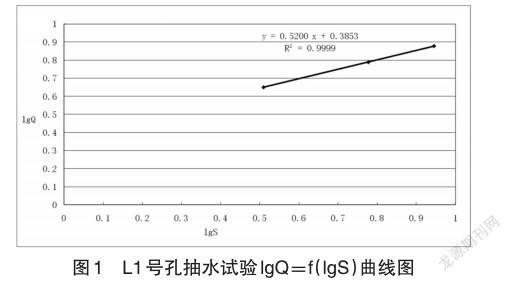
根据统计学原理,判定系数R平方值是趋势线拟合程度的指标,它的数值大小可以反映趋势线的估计值与对应的实际数据之间的拟合程度,拟合程度越高,趋势线的可靠性就越高。判定系数R平方值是取值范围在0~1之间的数值,当趋势线的R平方值等于1或接近1时,其可靠性最高,反之则可靠性较低[9]。
由于lgQ=f(lgS)曲线的线性拟合的判定系数R平方值最接近1,其拟合程度最高,可靠性最高,可以判断该抽水试验Q-S曲线类型为幂函数型。
(2)曲度法。2次以上(含2次)降深的抽水试验均可采用曲度法进行曲线类型判断。
曲度n是表征曲线弯曲程度的数值,不同的曲度对应不同的抽水试验曲线类型:当n=1时,为直线型;当n=1~2时,为幂函数型;当n=2时,为抛物线型;当n>2时,为对数型[10]。
曲度n的公式为n=(lgS1-lgS2)/(lgQ1-lgQ2)(公式(7))
将L1号孔抽水试验数据代入公式(7),该钻孔抽水试验有3组数据,排列组合可计算出3个曲度n值,分别为1.88、1.94、1.92,平均值1.91,各数值和平均值均介于1~2之间,由此可以判断该抽水试验曲线类型为幂函数型,与图解法结论一致。
3.2.2曲线方程计算
确定钻孔抽水试验Q-S曲线经验方程一般采用国家煤矿安全监察局编制的《煤矿防治水规定释义》中介绍的方法,即先用作图法判断Q-S曲线类型,再用图解法或最小二乘法确定经验方程[7]。在曲线类型判断的基础上,可进行曲线方程的计算。曲线方程计算一般有两种方法,即最小二乘法和图解法。
(1)最小二乘法。最小二乘法(又称最小平方法)是一种数学优化技术。它通过最小化误差的平方和寻找数据的最佳函数匹配。利用最小二乘法可以简便地求得未知的数据,并使得这些求得的数据与实际数据之间误差的平方和为最小。最小二乘法还可用于曲线拟合。
在抽水曲线方程计算过程中,可利用最小二乘法计算各曲线方程(公式(3)、公式(4)、公式(5)、公式(6))中的待定系数。
首先计算L1号孔抽水试验的S0(S/Q)、lgQ、lgS(见表2),根据抽水曲线类型判断,L1号孔抽水试验曲线类型为幂函数型。
将表2中的数据分别代入公式(11)、公式(12)计算得到公式(5)的待定系数m=1.921、n=2.425。
因此计算出L1号孔抽水试验曲线方程为lgQ=0.5206lgS+0.3847(公式15)。
(2)图解法。根据抽水曲线类型判断,L1号孔抽水试验曲线类型为幂函数型。在将表2中L1号孔抽水试验数据输入内容输入到EXCEL表格中,以lgS为横轴,lgQ为纵轴,按lgQ=f(lgS)曲线绘制离散点(见图1)。对离散点添加幂函数趋势线并显示公式,(如图1),其显示的线性方程为y=0.5200x+0.3853[公式(17)],因此该幂函数型(L1号孔抽水试验)曲线方程为lgQ=0.5200lgS+0.3853[公式(18)]。
3.2.3曲线方程的确定
对比最小二乘法和图解法计算的曲线方程可以看出,二者基本一致,由于图解法采用计算机EXCEL软件进行的计算,结果更精确,因此本文最终确定采用图解法计算的方程,即L1抽水试验曲线方程为公式(18)。
3.2.4单井回灌率计算
将L1号孔回灌试验最大升程7.17m作為降深S代入公式(19),计算出出水量Q=6.763L/s,即推算降深7.17m时单井出水量为6.673L/s。最后将推算的涌水量Q代入公式(2)中,计算出L1号孔单井回灌率X为89.7%。
4.结论
(1)对于3次以上(含3次)降深的抽水试验,采用EXCEL图解法判断曲线类型较为简便快捷;对于2次降深的抽水试验,只能采用曲率法进行判断。(2)采用最小二乘法计算曲线方程的过程中由于计算过程较复杂,如果不借助编程或EXCEL软件,计算复杂,费时费力,还容易出错,因此采用EXCEL图解法更简便、精确。(3)由于采用曲线方程推算涌水量有一个外延极限,根据1978年地质矿产部编制的《水文地质手册》,直线型曲线方程的外延极限为抽水试验最大降深的1.5倍~1.75倍,抛物线型、幂函数型和对数型曲线方程的外延极限为抽水试验最大降深的1.75倍~2倍。因此,要求我们在进行抽水、回灌试验时,抽水试验最大降深和回灌试验最大升程相差不易过大。(4)该计算方法科学、合理,计算过程简单、易操作,可在浅层地热能调查和地下水地源热泵勘查、设计过程资料整理中参考。
参考文献:
[1]周爽.浅谈浅层地温能[J].吉林农业, 2011, 262(12):248.
[2]王树星,宋亮,梁云汉.淄博市周村区浅层地温能开发利用资源潜力评价[J].山东国土资源, 2018, 34(12):42-47.
[3]殷焘,赵辉,毕建新.烟台市城区浅层地热能评价[J].山东国土资源, 2018, 34(12):48-53.
[4]孙文广,冷旭勇,王飞,等.郓城县浅层地热能勘查评价[J].山东国土资源, 2015, 31(1):36-39.
[5]马哲民,仝路,贾琛,等.山东省菏泽市城区岩溶热储回灌试验[J].山东国土资源, 2018, 34(11):52-57.
[6]周世海,杨询昌,梁伟,等.德州市城区地热水人工回灌试验研究[J].山东国土资源, 2007, 23(9):11 14.
[7]国家煤矿安全监察局.煤矿防治水规定释义[M].徐州:中国矿业大学出版社,2009:227-235.
[8]李本军,来永伟. Q-S曲线判定及问题探讨[J].中国煤炭地质, 2012, 24(9):41-43.
[9]吴群英,林亮.应用数理统计[M].天津:天津大学出版社. 2004.
[10]汪民,殷跃平,文冬光,等.水文地质手册(第二版)[M].北京:地质出版社, 2012.
