HRB335钢多轴疲劳寿命预测的改进临界面模型

秦胜欢，赵 钢，帅 韬，张克实,2

(1.广西大学土木建筑工程学院，南宁 530004；2.南宁学院土木与建筑工程学院，南宁 530200)

0 引 言

实际机械零部件大都在循环载荷下工作，疲劳破坏是其常见的破坏形式[1-2]。从应力状态分析，疲劳可以分为单轴疲劳和多轴疲劳。单轴载荷循环下材料只受到单向的应力;多轴载荷循环时材料的应力和应变分量分别有2个或多个,并且多轴载荷循环又可分为比例加载和非比例加载，其区别在于比例加载时主应力(或主应变)方向不发生变化，而非比例加载过程中主应力(或主应变)方向是变化的。在多轴非比例循环加载时，应力及应变主轴会发生周期性转动，使得材料内部更多的滑移系开动，从而产生不同方向及位置的疲劳裂纹，呈现非比例附加强化/软化现象[3-8]。与比例加载条件下相比，多轴非比例加载下的疲劳破坏规律复杂，并且难以确定疲劳损伤控制参量，给疲劳寿命分析带来很多困难。目前，对多轴疲劳问题，主要还是通过不同的等效方式参照单轴疲劳来进行分析，常规的方法包括等效应变法、能量法和临界面法等。在此基础上，一些学者针对不同条件下的多轴疲劳提出了一些新的寿命预测方法。如ZHOU等[9]将临界面法中的FS模型和SWT模型结合起来，提出了一种考虑剪切和拉伸影响的多轴疲劳寿命预测模型；KAMAL等[10]结合连续介质损伤力学和包含临界面法的遗传算法，提出了一种混合的多轴疲劳寿命估算方法，并用SS304钢的疲劳试验验证了该方法的适用性；ZHU等[11]提出了一种通过单轴疲劳试验确定基于能量的等效损伤参数的多轴疲劳寿命预测方法，并利用316L钢的疲劳试验验证了该方法的有效性；张小元等[12]在Q235钢大量试验的基础上，提出了一个考虑临界面法向正应变作用的模型，该模型对Q235钢在多轴比例及非比例加载条件下疲劳寿命的预测效果较好。但这些模型很大程度上是现象学模型，多数都通过添加需要用系列试验加以标定的模型参数来增加其路径适应性，其预测精度和适用性需进一步通过试验来进行检验并加以改进。

针对多轴疲劳寿命评估问题，作者以HRB335钢为研究对象，在5种加载路径下进行不同恒应变幅控制下的单轴及多轴非比例加载低周疲劳试验，在此基础上标定等效应变法、KBM临界面模型和引入拉伸因子的临界面模型(拉伸因子模型)[12]的参数，对比分析各模型对多轴疲劳寿命预测的有效性；考虑临界面法向正应变作用和非比例加载的影响，引入路径非比例度和材料附加强化参数对拉伸因子进行修正，建立了修正拉伸因子模型并对该模型的有效性进行了验证。

1 试验方法与试验结果

试验材料为柳钢生产的低合金热轧钢，牌号为HRB335，产品标准为GB/T 3274-2007。根据厂家提供的检验报告，该钢的主要化学成分见表1，碳当量Ceq为0.41，弹性模量为210 MPa，屈服强度为355 MPa，抗拉强度为520 MPa，断后伸长率为27.5%，泊松比为0.3。

表1 HRB335钢的主要化学成分(质量分数)

采用薄壁圆管试样进行单轴和多轴疲劳试验，具体尺寸见图1；在联合拉扭加载下，试样试验段可呈现复杂应力、应变状态。薄壁圆管试样经过钻孔、钼丝切割、粗精车削、磨削等工序，加工精度为IT8～IT7。为进一步降低刀痕和表面硬化层的影响，圆管试样内、外表面均进行了抛光处理，抛光后的表面粗糙度Ra为3.2～1.6 μm，同时用防锈油均匀涂抹内、外表面以避免锈蚀。以上措施能够保证试验结果的分散性在合理范围内。

图1 试样截面尺寸Fig.1 Sectional dimension of specimen

在MTS809型电液伺服拉扭试验机上进行疲劳试验，采用应变控制加载方式，应变比Rε为-1，平均应变为0，加载路径分别为轴向拉压、纯扭、圆形、菱形和蝶形等5种，如图2所示，图中：ε为轴向应变；γ为剪应变。

图2 加载路径示意Fig.2 Diagram of loading paths

轴向拉压和纯扭路径为单轴加载方式，加载波形均为正弦波，波形表达式分别为

ε=εasinωt

(1)

γ=γasin(ωt-φ)

(2)

式中：εa和γa分别为轴向应变幅和剪应变幅；ω和t

分别为角频率和时间；φ为ε和γ之间的相位差。

圆形、菱形和蝶形路径加载为多轴非比例加载。圆形和菱形路径加载波形分别为正弦波和三角波(相位差都是90°)，蝶形路径加载时其轴向波形为三角波，扭转方向波形为梯形波。相应的加载波形如图3所示，加载频率均为1 Hz，室温环境。受材料微结构如内部微小夹杂物和初始缺陷，以及加工工艺、表面状态等外部因素的影响，在同一加载条件下试样的疲劳寿命也会有明显差别[13]。为保证测试结果的分散性合理并具有统计意义，参照文献[13]，轴向拉压路径下各应变幅下的试样数量均为3个，其他加载路径下的试样数量为2～3个，只有试探性的等效应变幅为0.001 5下纯扭和圆形路径的疲劳试验，试样数量各为1个。不同加载路径下的试验参数及疲劳寿命结果见表2，表中：Δεeq/2为Von Mises等效应变幅；Nf为疲劳寿命。

图3 多轴非比例加载波形Fig.3 Loading waveforms for nonproportional multiaxial loading: (a) circular path; (b) rhombic path and (c) butterfly path

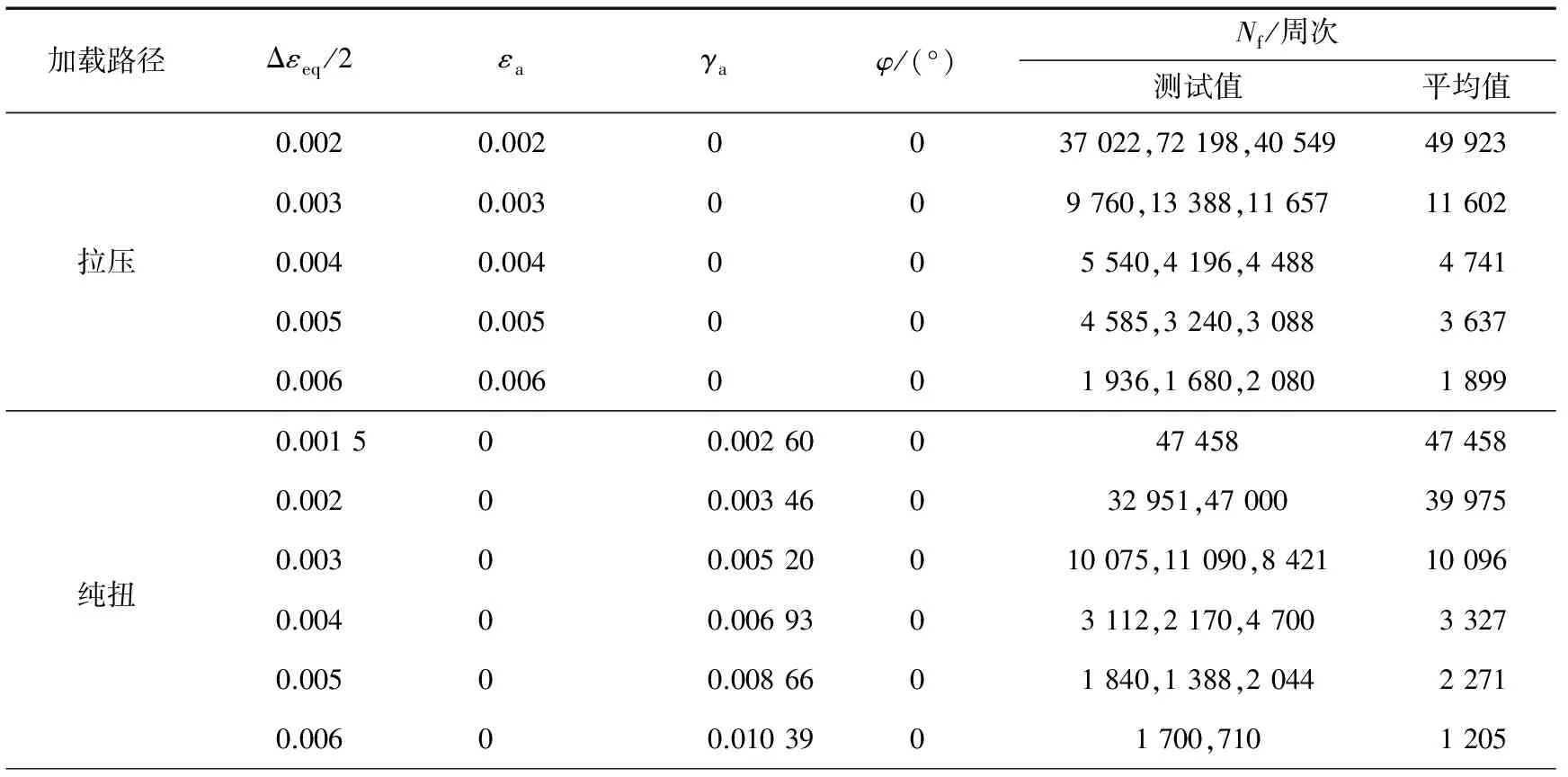
表2 HRB335钢低周疲劳试验参数及试验结果

由表2中的数据绘制等效应变幅-疲劳寿命曲线。由图4可看出：单轴拉压路径下试样的疲劳寿命最长，纯扭路径下次之，3种多轴非比例加载路径的疲劳寿命都明显低于上述2种单轴加载路径下的疲劳寿命，其中圆形路径下的疲劳寿命最短，菱形路径下小应变幅下的疲劳寿命短于蝶形路径下的疲劳寿命，应变幅增大后疲劳寿命又长于蝶形路径下的疲劳寿命。

图4 不同路径加载下试样的等效应变幅与疲劳寿命的关系Fig.4 Relationship between equivalent strain amplitude and fatiguelife of specimens with different loading paths

2 疲劳寿命预测

2.1 等效应变法预测疲劳寿命

一般基于Manson-coffin方程[14-15]对单轴加载条件下材料的低周疲劳寿命进行预测。该方程经过MORROW等[16]的发展和修正后，对于拉压低周疲劳的表达式为

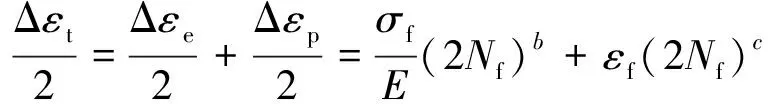
(3)

式中：Δεt/2为总应变幅，在单轴拉压加载下近似为轴向应变幅；Δεe/2为弹性应变幅；Δεp/2为塑性应变幅；σf，εf分别为疲劳强度系数和疲劳延性系数；b，c分别为疲劳强度指数和延性指数；E为材料弹性模量。

HRB335钢的实测弹性模量为203 052 Pa。由图4可知，在双对数坐标下，HRB335钢在单轴拉压加载下的应变幅-疲劳寿命曲线近似为一条直线，因此可以通过线性拟合得到式(3)中的参数如下：σf=524 MPa，εf=0.530，b=-0.053，c=-0.557。

将式(3)引入到多轴低周疲劳模型中，以等效应变幅作为疲劳参量，得到方程[17-18]如下：

(4)

在多轴疲劳分析中常用的等效应变准则有最大主应变准则、最大剪应变准则和Von Mises等效应变准则。作者采用的是Von Mises等效应变准则，该准则中等效应变的定义为

(5)

式中：εeq为等效应变；ε1，ε2，ε3为主应变；ν为泊松比。

在单轴拉压加载下，Δεt≈Δεeq，因此可用单轴拉压试验结果标定式(4)中的参数，随后利用式(4)对纯扭、圆形、菱形和蝶形路径下的疲劳寿命进行预测。不同加载路径下预测疲劳寿命与实测疲劳寿命的对比如图5所示。预测点在三倍误差范围的上侧意味着预测寿命大于实测寿命3倍以上，用此预测结果偏于危险；预测点在三倍误差范围的下侧则偏于安全，因为实际寿命比预测寿命长。

由图5可以看出：用等效应变法预测单轴拉压和纯扭加载下试样疲劳寿命的效果较好，预测点分布在实测寿命与预测寿命相等的虚线附近，仅个别点位于三倍误差范围之外；但是用该法预测的多轴非比例加载条件下的疲劳寿命都偏出三倍误差范围之外，且都偏于危险，预测寿命偏差最大的是圆形路径加载条件，误差最大高达10倍以上。

图5 等效应变法预测的疲劳寿命与实测疲劳寿命的关系Fig.5 Relationship between fatigue life prediction byequivalent strain method and test fatigue life

2.2 KBM模型预测疲劳寿命

BROWN等[19]将材料在疲劳循环过程中最大剪应变γmax所在的平面定义为临界面，认为多轴低周疲劳微裂纹的萌生或扩展由临界面上的剪应变γ和法向正应变εn这2个应变参量控制。基于此理论，KANDIL等[20]提出一种多轴疲劳寿命预测临界面模型，又称为KBM模型，其表达式为

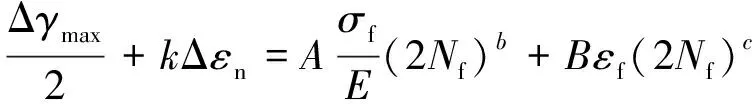
(6)

A=(1+νe)+k(1-νe)

(7)

B=(1+νp)+k(1-νp)

(8)

式中：Δγmax/2为临界面上最大剪应变幅；Δεn为临界面上法向正应变变程；k为与材料相关的经验常数，可由纯扭作用下的疲劳试验数据标定，对于HRB335钢，k取0.8[21]；νe，νp分别为弹性泊松比和塑性泊松比。

σf，εf，b，c的物理意义与式(3)中相同，其值可由单轴拉压疲劳试验结果拟合得到[22]。临界面上Δγmax和Δεn计算公式分别为

Δγmax=εa{[(1+νeff)sin 2θc-

λcos(2θc)cosφ]2+[λcos(2θc)sinφ]2}1/2

(9)

λsin(2θc)cosφ]2+[λsin(2θc)sinφ]2}1/2

(10)

(11)

式中：νeff为等效泊松比；εe，εp分别为加载应变的弹性部分和塑性部分；λ为扭转应变幅与拉压应变幅之比；θc为一个加载循环中圆管试样某点处的最大剪切方向与圆管轴向的夹角。

θc的计算公式[23]为

(12)

对于HRB335钢薄壁圆管试样，5种加载路径及相应应变幅下，KBM模型损伤参量Δγmax/2+kΔεn的值见表3。

表3 不同加载路径下HRB335钢KBM模型的损伤参量Table 3 Damage parameters of KBM model for HRB335steel with different loading paths

将表3中不同加载路径下的损伤参量代入式(6)，计算得到KBM模型预测的疲劳寿命，其与实测寿命的对比如图6所示。对比图5和图6可以看出，对于HRB335钢在5种加载路径下的疲劳寿命预测，KBM模型得到的结果比等效应变法准确得多，但是对于蝶形和圆形路径还是出现了处于三倍误差范围外危险侧的预测结果。

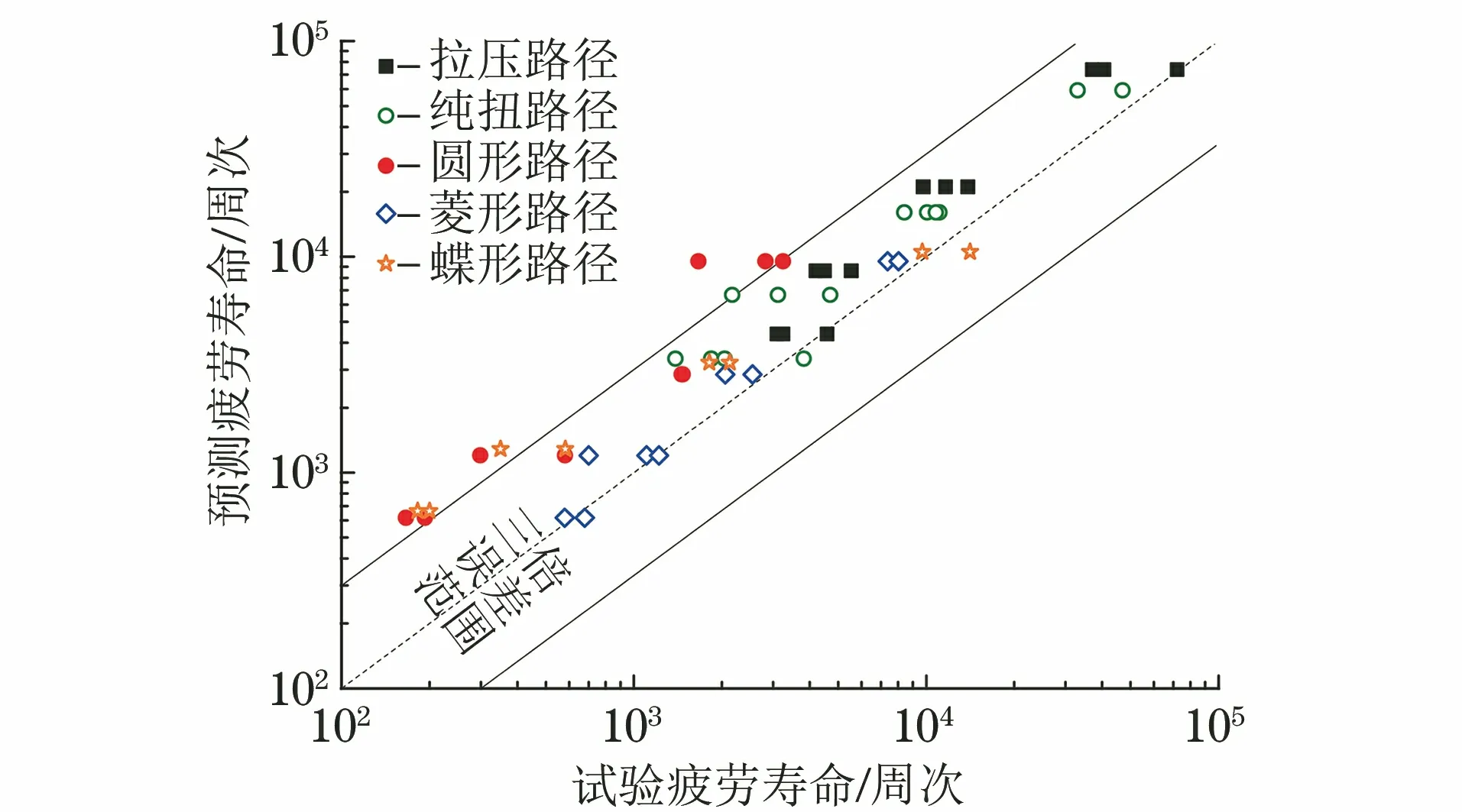
图6 KBM模型预测的疲劳寿命与实测疲劳寿命的关系Fig.6 Relationship between fatigue life prediction byKBM model and test fatigue life

2.3 拉伸因子模型预测疲劳寿命

上述KBM模型以及其他临界面模型是在Morrow公式的基础之上，通过大量的试验数据修正Morrow公式中的疲劳参量而建立的。公式的修正一般通过引入一些参数而实现，而这些参数的物理意义往往并不确定。

很多学者都在试图寻找到一个即能够便于工程应用又能有明确物理意义的多轴疲劳寿命预测模型。张小元等[12]通过对Q235钢的大量多轴疲劳试验数据的分析，总结出了一个考虑临界面上法向正应变作用的临界面模型，该模型的表示形式为

(1+νp)εf(2Nf)c

(13)

式中：Δεn/2为临界面上法向正应变幅；μ为考虑加载路径的拉伸因子。

拉伸因子不需要由系列试验标定，直接由公式计算得到；其计算公式为

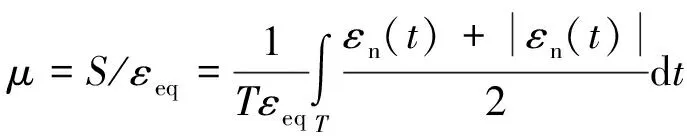
(14)

式中：εn(t)为临界面上法向正应变随时间t的变化函数[12]；S为临界面上法向正应变在一个循环周期T内的积分面积大小。

由式(14)计算得到拉压路径、纯扭路径、圆形路径、菱形路径、蝶形路径加载下的拉伸因子分别为0.6，0，2，1.57，0.96。则HRB335钢拉伸因子模型中的损伤参量Δγmax/2+μΔεn/2的值见表4。

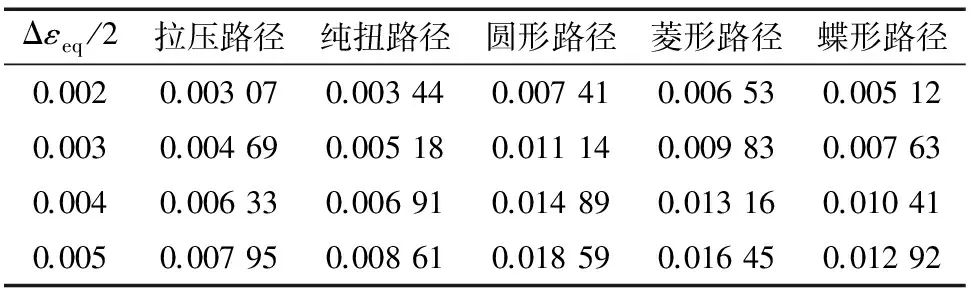
表4 不同加载路径下HRB335钢拉伸因子模型的损伤参量Table 4 Damage parameters of stretching factor model forHRB335 steel with different loading paths

将表4中不同加载路径下的损伤参量代入式(13)，得到拉伸因子模型预测的疲劳寿命，其与实测结果的关系如图7所示。由图7可以看出，拉伸因子模型对不同加载路径下的疲劳寿命的预测结果基本上集中在三倍误差范围之内，预测能力较好，但是对于蝶形路径在高应变区会出现偏危险的预测结果。

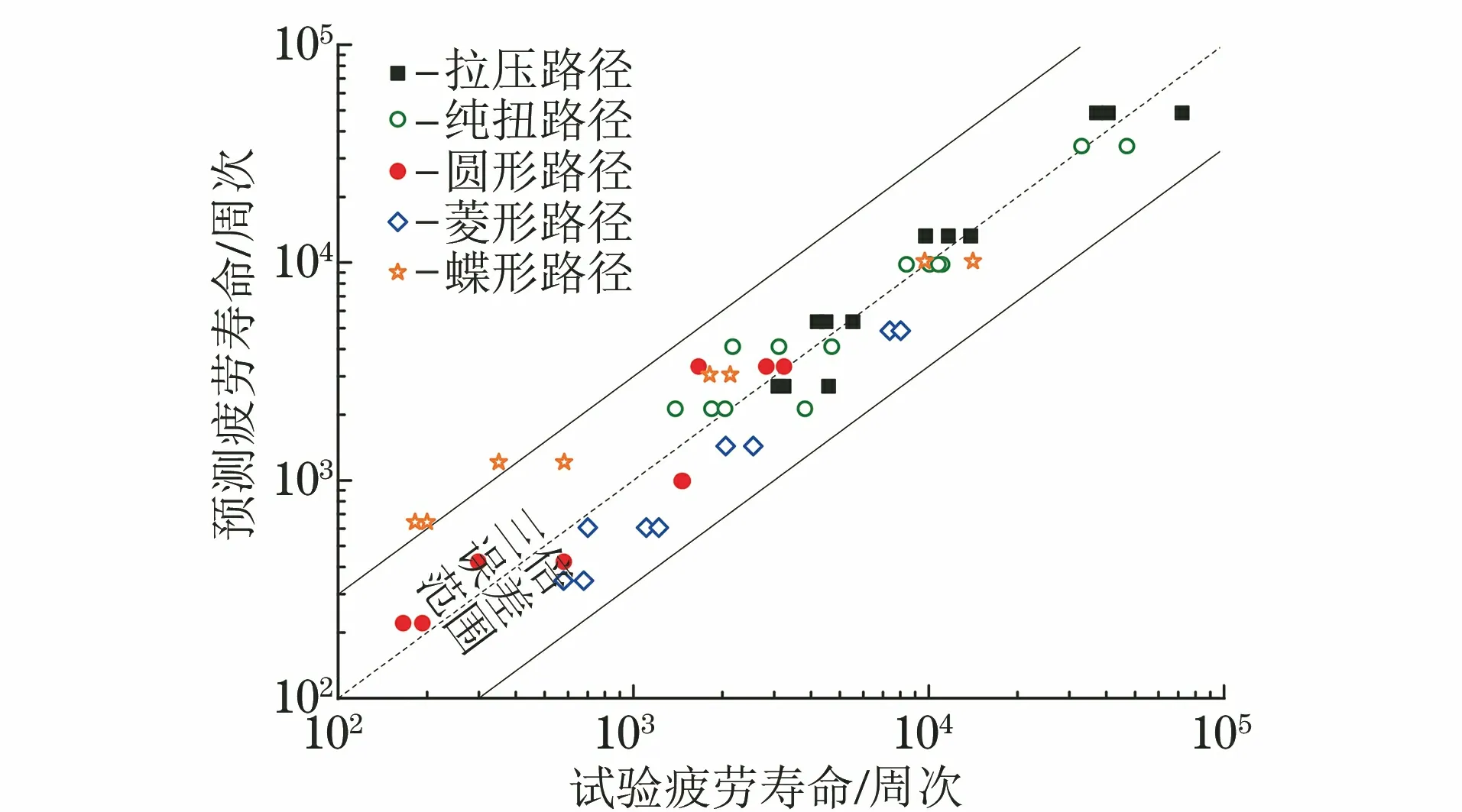
图7 拉伸因子模型预测的疲劳寿命与实测疲劳寿命的关系Fig.7 Relationship between fatigue life prediction bystretching factor model and test fatigue life

2.4 修正拉伸因子模型预测疲劳寿命

因为没有考虑加载路径非比例度对疲劳寿命预测的影响，上述3种方法对多轴非比例加载疲劳寿命的预测结果与实测结果都存在一些差距。在上述3种方法中，拉伸因子模型不含经验常数，便于使用，且预测的结果也较为接近实测结果，故作者在该模型的基础上，对拉伸因子进行了路径非比例度和材料附加强化的修正。为反映加载路径的非比例程度，参考CHEN等[24]的研究，定义了一个路径非比例因子Φ，其表达式为

(15)

式中：Aθ,max为在以γθ,max为极径，以θ为极角的极坐标中，当θ取值范围从0到2π时γθ,max包络的面积；γθ,max表示与试样轴线成θ角的平面上的最大剪应变；Amax为当θ的取值范围从0到2π时，以γθ,max的极值(γθ,max)max为半径的圆的面积。

不同加载路径下γθ,max-θ的关系如图8所示，计算得到的圆形、菱形和蝶形3种路径下的非比例因子分别为0.82，0.39，0.48。

图8 不同加载路径下的γθ,max-θ关系图Fig.8 γθ,max-θ diagram under different loading paths: (a) circular path; (b) rhombic path and (c) butterfly path

材料在受到非比例加载时会产生附加强化效应[25]，并且不同材料受到的强化程度不同。因此，定义一个附加强化参数g来表征强化程度，其表达式[26]为

(16)

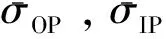
对于HRB335钢，根据实测相同应变幅下圆形路径与比例加载路径的峰值等效应力计算得到的g为0.173 6。定义一个考虑多轴加载路径非比例度和材料附加强化的拉伸因子μ′，表达式为

μ′=(1+g)μΦ

(17)

将材料附加强化参数和不同路径下的非比例因子、拉伸因子代入式(17)，计算得到圆形路径、菱形路径、蝶形路径下考虑多轴加载非比例度和材料附加强化的拉伸因子μ′分别为1.77，1.4，1.14，则损伤参量Δγmax/2+μ′Δεn/2的值如表5所示。考虑多轴加载路径非比例度和材料附加强化的拉伸因子μ′不需要通过系列疲劳试验标定，可直接由描述加载路径的参数或材料常规试验测试参数得到，便于应用。用μ′取代μ代入式(13)，即得到考虑多轴加载路径非比例度和材料附加强化的拉伸因子模型(简称为修正拉伸因子模型)，如下：

(1+νp)εf(2Nf)c

(18)

表5 考虑非比例加载和材料附加强化的拉伸因子模型的损伤参量

将表5中的损伤参量代入修正拉伸因子模型，即式(18)，预测得到的疲劳寿命与实测结果的关系见图9。由图9可知，考虑多轴加载路径非比例度和材料附加强化的修正拉伸因子模型对圆形、菱形和蝶形多轴路径的疲劳寿命预测结果都位于三倍误差范围内。与图5、图6和图7对比可知，修正拉伸因子模型对疲劳寿命的预测结果明显优于等效应变法、KBM模型和拉伸因子模型。

图9 修正拉伸因子模型预测疲劳寿命与实测疲劳寿命的关系Fig.9 Relationship between fatigue life prediction byimproved stretching factor model and test fatigue life

使用式(18)对HRB335钢的所有路径疲劳试验结果进行拟合，结果如图10所示。由图10可以看出，5种加载路径下所有测试点数据较均衡地分布于修正拉伸因子模型曲线的两侧，其分散性远小于以等效应变幅为参数的结果(图4)。

图10 修正拉伸因子模型对HRB335钢疲劳试验结果的拟合情况Fig.10 Fitting effect of fatigue test results of HRB335 steelwith improved stretching factor model

用文献[12]中Q235钢和文献[27]中304不锈钢的多轴疲劳试验结果对新模型的适用性进行检验，结果如图11所示。由图11可知，修正拉伸因子模型的疲劳寿命预测值除了个别点外，都位于三倍误差范围内，而且给出了偏于安全的估计结果。

图11 修正拉伸因子模型对Q235钢和304不锈钢的疲劳寿命预测结果与试验结果的关系Fig.11 Relationship between fatigue life prediction of Q235 steel and304 stainless steel by improved stretching factor model and test results

3 结 论

(1) 实测HRB335钢在纯扭路径与单轴拉压路径下的疲劳寿命相近，而多轴非比例加载路径下的疲劳寿命明显降低，圆形路径下的疲劳寿命最短。采用Von Mises等效应变幅为疲劳参数的等效应变法预测疲劳寿命时，对于圆形路径加载条件，预测寿命远比实际寿命高，最大超过10倍。

(2) 临界面法的KBM模型对3种多轴非比例路径加载的疲劳寿命预测结果明显好于等效应变法，但对于圆形路径和蝶形路径，仍有相当数量的预测结果超出三倍误差范围。

(3) 文献[12]建议的拉伸因子模型对疲劳寿命的预测结果优于等效应变法和KBM模型，但对于蝶形路径加载条件，仍有少量寿命预测结果超出了三倍误差范围。

(4) 考虑加载路径非比例度和材料附加强化的修正拉伸因子模型，对所有加载路径的HRB335钢的疲劳寿命预测值都位于三倍误差范围内，并且对Q235钢和304不锈钢多轴疲劳寿命的预测也与实测结果吻合；修正模型中的拉伸因子、路径非比例因子和附加强化参数均可直接由描述加载路径的参数或材料常规试验参数得到，不需专门安排试验进行标定，便于工程应用。