基于贝叶斯网络的电能表状态评估方法
2021-12-09唐冬来杨帆付世峻何鹏陈武陈科宇
唐冬来,杨帆,付世峻,何鹏,陈武,陈科宇
(1.四川中电启明星信息技术有限公司,四川 成都 610041;2. 重庆邮电大学 通信与信息工程学院,重庆 400065; 3. 国网四川省电力公司绵阳供电公司,四川 绵阳 621000)
随着国家电网有限公司“三型两网”建设工作的不断推进,对电能计量管理精益化要求日益增高[1]。电能表作为电能计量的重要装置,其状态运行正常与否和供电公司、用电客户的利益息息相关[2-6]。传统的电能表状态检验以周期性检定为主[7],评估的指标权重单一,不能满足跨地域的电表运行状态评估需求[8-9]。同时,电能表的现场状态检验工作缺少监管手段,电能表状态检验效率低[10]。
国内外许多学者对电能表状态评估提升工作做了大量研究。电能表状态评估研究成果主要分为固定评价指标体系和动态评价指标体系。在固定评价指标体系方面,采用人为主观设定的电能表状态评价指标体系对电能表进行评估。固定评价指标体系可根据可靠性维护、安全域、家族缺陷、误差特征等因素人为设立指标[11-14],其指标体系设置简单,但对省级电力公司数百万计的电能表状态评估适应性不强。动态评价指标体系方面,采用决策树群和大数据方法对电能表状态评估指标体系进行调整[15-16],可有效解决评估指标集有效生产的问题,但由于动态评价指标体系采集电能表数据源于人工录入,且不能对评估指标集的权重进行调整,因此电能表状态评价质量不高。
为解决传统电能表现场状态评估过程中存在的指标权重单一、评估效率低等问题,本文提出一种基于贝叶斯网络的电能表状态评估方法。在对电能表状态评估数据降维采集的基础上,采用无监督学习法建立电能表状态评估矩阵,并结合区域特征进行指标权重动态调整。然后,通过贝叶斯网络对电能表状态进行评估。最后,将本文所提方法应用到某地区供电公司,以验证本文所提方法在评估准确性和效率方面的优越性。
1 电能表状态评估框架
本文所述的基于贝叶斯网络的电能表状态评估方法框架如图1所示,主要分为电能表状态评估特征数据提取、状态评估指标矩阵、评价权重调整和电能表状态评估4个部分。
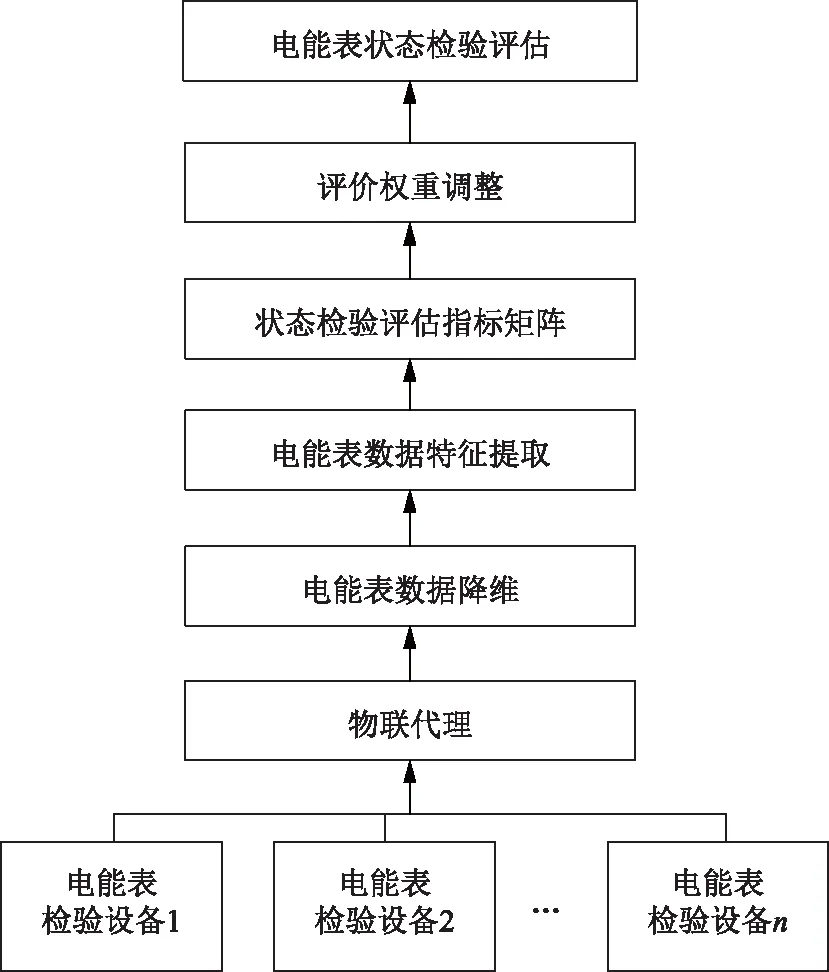
图1 电能表状态评估框架Fig.1 Energy meter condition evaluation framework
在电能表状态评估特征数据提取环节,首先通过物联代理设备在线汇聚各检验设备的电能表状态评估数据,然后对检验设备的电能表状态评估数据进行降维处理,避免全量数据上传造成的计算效率低的问题。在状态评估指标矩阵建立环节,采用无监督学习法对电能表基础档案、批次运行状态和运行状态方面进行分析,并建立电能表状态评估指标矩阵;在评价权重调整环节,结合各供电公司地域性电能表运行特点,对电能表评价权重进行动态调整;在电能表状态评估环节,结合电能表指标权重的情况,采用贝叶斯网络对电能表的状态进行评估。
2 电能表状态评估模型
2.1 电能表状态特征数据提取
2.1.1 电能表检验数据物联采集
近年来,国家电网有限公司启动了带物联功能的电能表校验工具研究[17],通过在电能表校验工具上加装物联设备,实现电能表状态监测数据的物联上传,从而解决传统电能表检验设备数据无法上传的问题。
2.1.2 电能表状态检验数据降维
主成分分析(principal component analysis,PCA)算法是一种数据降维方法,通过线性变换将输入的高维向量数据转换为低维度数据。PCA算法一般用于提取数据的主要特征和高维数据降维[18]。
电能表状态检验数据主要来源于电能表的档案数据和电能表检验设备的失压、失流、电压逆相序、全失压、断相等状态监测数据。若对电能表检验设备全量上传的检验数据进行分析,则会造成电能表评价算法模型运行效率低的问题。采用PCA算法对电能表状态检验数据进行降维处理,可提高电能表状态评估模型的运行效率,避免全量数据上传造成的计算效率低的问题。在电能表特征数据降维后,开展电能表状态检验数据的特征值提取。
2.2 状态评估指标矩阵
近邻传播(affinity propagation,AP)聚类算法不需要指定聚类数量,具有聚类结果误差小的优势,但算法较为复杂,在处理多维大量数据时,AP聚类需要的时间比较长[19]。
电能表状态评估指标是综合考虑电能表运行的可靠性、电能表生产厂商质量风险控制等因素的评估[20]。电能表状态评估需要对现有的电能表特征进行聚类,从而计算出共性的电能表检验特征指标。为提高AP聚类的速度,对现有AP聚类算法中的相似度矩阵偏向函数进行改进。
采用改进AP聚类方法对电能表运行状态数据进行分析。涉及的电能表数据包括电量、电压、电流,以下以电能表电流数据为例进行介绍。设电能表1的电流运行数据as的离散特征为ga,电能表2电流运行数据bs的离散特征为gb,离散特征点的距离采用欧式距离计算,设特征权重系数为wa,2个离散特征点的相似度
zh=-[waga+(1-wa)gb].
(1)
离散特征点gc可表示为
(2)
式中:hji和hki分别为数据点i的2个离散特征点j、k的最小值;ne为数据点总数。
偏向函数为相似度矩阵主对角线的值u,合理选取偏向函数,即可减少迭代次数,AP聚类算法在多次迭代后,数据基础(data basis,DB)指标DB可作为电能表离散特征的收敛函数。设电能表电流曲线相似度矩阵的对角线中位数为ea,AP聚类的搜索阈值为λ,可得:
u=ea+λDBmin.
(3)
式中DBmin为DB指标收敛函数的最小值。
设聚类的数量为ng,聚类的中心为Cm,两类电表的数据点到数据中心的距离分别为Qa和Qb,聚类DB指标
(4)
通过AP聚类,建立电能表状态评估指标矩阵见表1。
2.3 评价权重动态调整
熵权法是对于指标体系中的某项值权重进行调整的方法,通过熵值来判断某个指标的离散程度,其熵值越小,则说明该指标对指标体系的影响越大[21]。
受地理环境、气候、温度等因素影响,电能表运行状态评估的特征值不尽相同[22]。为解决各省电力公司之间电能表运行状态的差异,结合各省电力公司地域性电能表运行特点,采用熵权法对表1中的电能表评价权重进行动态调整。
首先,根据专家经验值设定电能表运状态评估权重ω=(ω1,ω2,…,ωnb),其中nb为电能表状态检验指标集的总数。在生成聚类中心后,计算单个特征指标对电能表状态检验聚类中心的贡献度,设电能表特征指标聚类中心数为ka,随机选择的聚类中心i的特征负荷值为Lran,i,聚类中心i的特征值为lb,i,电能表状态评估特征指标的贡献度
(5)
电能表状态评估的特征指标权重
(6)
式中Pci为聚类中心i的特征指标的贡献度。
本文结合地区供电公司电能表运行特点,采用熵权法对初始电能表状态检验的权重进行更新,更新后的权重
(7)
式中φai为聚类中心i的特征指标权重。
2.4 电能表状态评估
贝叶斯网络可直观统计电能表状态评估各节点之间的因果关系,可进行双向推理获得准确的电能表状态评估值[23]。根据地区供电公司电能表运行特点进行电能表状态评估指标特征权重调整后,采用贝叶斯网络对电能表的状态进行评估。
设电能表状态评估特征指标的阈值越限事件概率为ua,电能表状态检验故障的发生概率为va,电能表状态检验特征指标个数为ke,在ua条件下的va条件概率
(8)
式中uai为电能表状态评估特征指标i的阈值越限事件概率。电能表状态评估的故障发生特征
(9)
通过式(9),可获得对电能表运行状态的评估结果。
3 电能表状态评估仿真流程
基于贝叶斯网络的电能表状态评估流程如图2所示。
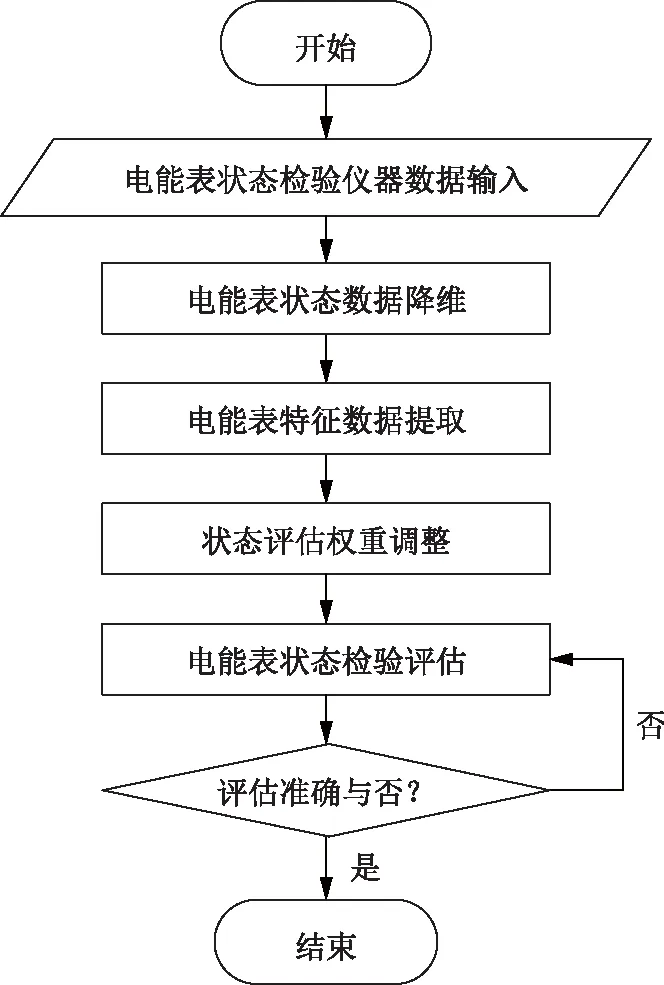
图2 电能表状态评估流程Fig.2 State evaluation process of electric energy meter
4 算例分析
采用本文所提的基于贝叶斯网络的电能表状态评估方法,对某省电力公司的高压三相电能表的现场检验数据进行评估,数据来源为现场电能表检验仪表远程上传的高压三相电能表现场校验数据。本文采用的计算机系统版本为Windows Sever 2016、16核心至强2.4 GHz中央处理器、32 GB内存,电能表的校验仪为国家电网有限公司计量中心2018年组织研究的新型现场校验仪。
在电能表状态评估中,首先选择电能表状态评估的指标权重作为评估的基准。然后选取文献[15]中的多决策树群电能表状态评估方法作为参照,与本文方法进行对比,以验证本文方法的有效性。
4.1 电能表状态评估指标权重选取
训练样本选择:某省电能表状态评估仪表100台,每台校验100只高压三相电能表现场检验数据,权重总分为100%。各指标权重见表2。

表2 电能表状态评估指标权重Tab.2 Weight of state evaluation index of electric energy meter
4.2 电能表状态评估运行时间分析
分别选择电能表状态评估仪表的数量为5、10、20、50、80、100、200,每台校验100只高压三相电能表现场检验数据,对比本文方法与多决策树群的电能表状态评估运行时间,结果见表3。
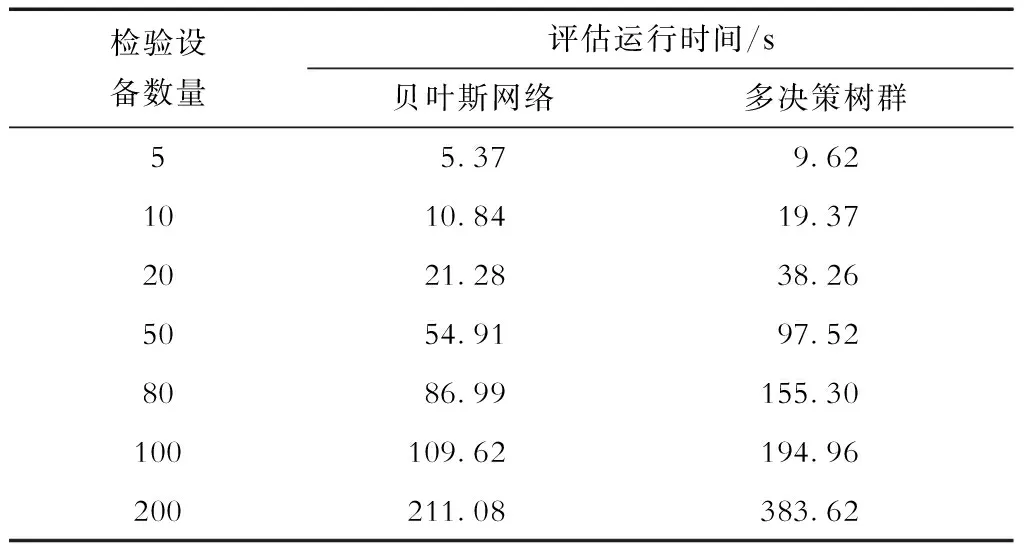
表3 电能表状态评估运行时间对比Tab.3 Comparison of running time of electric energy meter condition evaluation
由表3可见,在电能表状态评估数据提取时间方面,本文所提的基于贝叶斯网络的电能表状态评估方法优于多决策树群方法。
4.3 评估指标权重调整准确率分析
电能表评估权重调整准确率是衡量指标是否符合省级电力公司要求的关键指标,指标权重调整的准确率为调整正确的指标权重数量与调整的指标权重数量的比值。
选择电能表状态评估仪表的评估指标分别为运行时间、运行故障率、违约窃电信息表、运行误差、运行监测事件、运行监测异常,评估样本电表数量为100,对比本文所提基于贝叶斯网络的电能表状态评估方法与多决策树群的电能表状态评估方法的指标权重准确率,结果如图3所示。
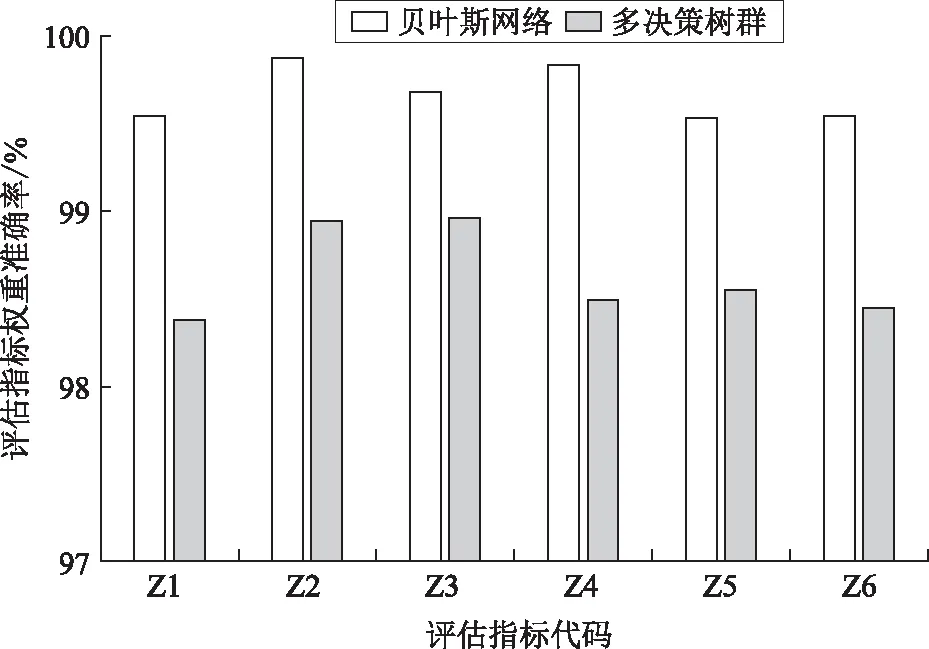
图3 电能表状态评估指标权重准确率对比Fig.3 Comparison of weight accuracy of state evaluation index of electric energy meter
由图3可见,在电能表状态评估指标权重调整准确率方面,本文所提基于贝叶斯网络的电能表状态评估方法优于多决策树群方法。
4.4 电能表状态评估准确率分析
电能表状态评估准确率是电能表状态评估的核心指标,其计算方法为评估正确的电能表数量除以评估的电能表总数。该数字的取值范围为0~1,数值越大,电能表状态评估准确率越高。
分别选择电能表状态评估仪表的数量为5、10、20、50、80、100、200,每台电能表状态评估仪表检验的电能表数量为100,对比本文方法与多决策树群的电能表状态评估准确率,对比结果见表4。
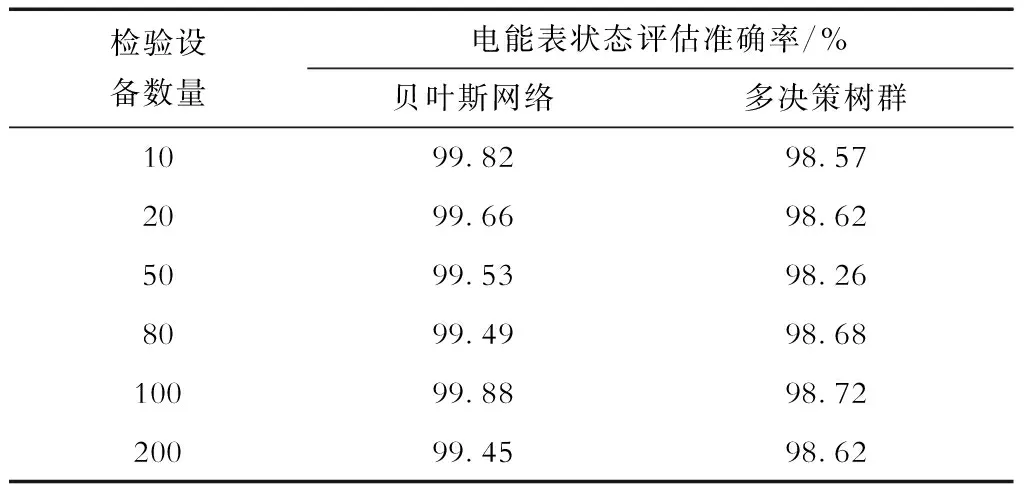
表4 电能表状态评估准确率对比Tab.4 Comparison of state evaluation accuracy of electric energy meter
由表4可见,在电能表状态评估准确率方面,本文所提的基于贝叶斯网络的电能表状态评估方法优于多决策树群方法。
4.5 电能表状态评估结果分析
文中方法的评估指标选择范围见表1,评估分值取值范围为0~100,90分以上为优秀,75~90分为良好,60~74.99分为合格,60分以下为不合格。选择某省电力公司100只高压三相电能表,采用文中方法进行电能表状态评估,评估结果见表5。

表5 电能表状态评估结果Tab.5 State evaluation results of electric energy meter
5 结束语
为解决传统电能表现场状态评估过程中存在的指标权重单一、评估效率低的问题,本文提出一种基于贝叶斯网络的电能表状态评估方法。在物联代理设备采集现场电能表校验基础档案、批次运行状态和运行状态的基础上,采用数据降维算法实现电能表检验数据的提取,以降低数据采集时间。其次,采用无监督学习方法建立电能表状态评估指标矩阵,并结合区域特征对电能表评价权重进行动态调整。然后,使用贝叶斯网络对电能表的运行故障发生概率进行评估,从而获得准确的电能表状态评估结果。
本文所述的方法在电能表状态评估指标权重调整方面还存在提升空间,后续将结合时间卷积网络对电能表指标评估权重调整做进一步研究。
