基于FPGA的直驱型风电场详细电磁暂态建模方法
2021-12-09雷肖龚文明张斯翔赵晓斌彭代晓
雷肖,龚文明,张斯翔,赵晓斌,彭代晓
(1.三峡机电工程技术有限公司,四川 成都610094;2.直流输电技术国家重点实验室(南方电网科学研究院有限责任公司),广东 广州510663)
为实现“双碳”目标,加快推进能源转型、构建以新能源为主体的新型电力系统势在必行[1]。广东地区拥有丰富的海上风能资源,根据《广东省国民经济和社会发展第十四个五年规划和2035年远景目标纲要》及《广东省海上风电发展规划(2017—2030年)(修编)》,“十四五”时期广东省将建成投产海上风电容量超8 GW,到2030年底达到30 GW,海上风电将是广东省未来新型电力系统的重要电源。
新型电力系统具有高比例可再生能源、高比例电力电子的双高特征,电力系统的控制与稳定特性将发生深层次变化,其安全稳定运行将面临重大挑战,例如:2016年澳大利亚发生的“9·28”高占比可再生能源脱网导致50 h大停电事故[2];电网中频繁观测到的宽频带、多形态振荡事件,威胁了电网设备的安全生产[3]。
为了保障大容量海上风电并网情况下电力系统的稳定运行,有必要对系统稳定性[4]、风电组网[5]、参数设计[6]、控制策略优化[7]等方面进行更详细的研究,由于包含大量电力电子设备,电磁暂态仿真分析是其中的关键环节之一。
现有仿真技术对设备级或小规模电力电子系统的电磁暂态分析已较为成熟。然而,在涉及到较大规模系统级的稳定性问题,尤其是考虑到多风电机组、多时间尺度动态特性相互影响时,电磁暂态仿真的计算量急剧增加,大型风电并网系统的多时间尺度电磁暂态仿真是目前尚未解决的关键问题之一[8]。
目前,风电场建模大致分为等值建模与详细建模2个主要技术方向。风电场等值建模[9-12]旨在保证风电场并网点动态响应不变或近似的条件下,将风电场等效聚合成1台或几台风电机组。等值模型能够有效降低风电场的阶数,因此能极大地减少仿真时间,被广泛用于涉及风电场的电力系统仿真分析中,并且风电场等值聚合方法本身也是一个研究热点。然而,由于进行了相当程度的简化,该方法只能用于风电场外部特性研究,无法直接反映风电场的内部特性,难以对风电场的内部控制进行有效测试。
风电场详细模型[13]是指完全保留风电场内部的网络拓扑与接线形式,包括主变压器、集电线路、机端变压器、变流器等设备,能够反映单台风电机组的运行控制特性。由于风电场本身是一个高阶的非线性系统,详细模型需要耗费大量计算资源,在进行风电机组控制保护半实物仿真测试中更是需要投入大量昂贵的实时仿真设备。高昂成本限制了风电场详细模型的应用。
针对以上问题,本文提出基于现场可编程门阵列(field programmable gate array,FPGA)的风电场详细建模方法[15],基于模型分割与并行计算技术,实现多台风电机组的高效求解。基于RT-LAB平台,建立包含脉冲宽度调制(pulse width modulation,PWM)开关特性的风电场详细模型。
1 风电机组模型
大型海上风电机组以永磁直驱型为主[16]。图1所示为1台并网永磁直驱风电机组[17],其中包括风轮、永磁发电机(PMSG)、定子侧变流器(SSC)、网侧变流器(GSC)、机端变压器(TRANS)、集电线路等。本节以机端母线为界,建立风电机组仿真模型。

图1 并网直驱风电机组Fig.1 Circuit diagram of grid-connected direct drive wind turbine
1.1 风轮
风轮将风的动能转化为转轴机械能,采用下式描述风电机组的机械功率特性[18]:
(1)
式中:Tm为风电机组机械转矩;Cp为风能利用系数;λ为叶尖速比;β为桨距角;ρ为空气密度;A为叶轮扫过面积;r为叶轮半径;vw为风速。
图2所示为不同风速(标注于各曲线处)下风电机组转速与输出机械功率关系曲线,其中风电机组转速与输出机械功率均为标幺值。在额定风速以下,风电机组捕获最大风功率;在额定风速以上,将风电机组输出功率限制为额定值。
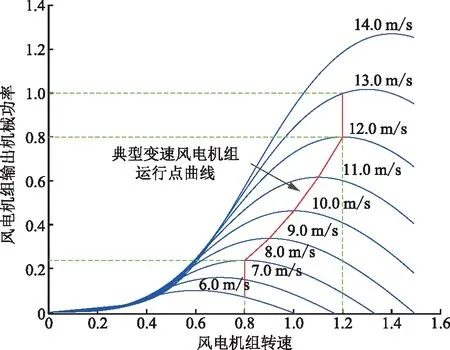
图2 不同风速下风电机组转速与输出机械 功率关系曲线(桨距角为0°)Fig.2 Relationship curves of rotate speed and output mechanical power of wind turbine at different wind speeds (pitch angle is 0°)
1.2 发电机
发电机将转轴机械能转化为电磁能。对于工作在额定工作区域的永磁直驱来说,忽略磁饱和效应,并假定气隙磁通为正弦分布,可以得到同步坐标系下的常系数线性微分方程模型。其电压方程为:
(2)
磁链方程为:
(3)
电磁转矩Te方程为:
Te=p(φdiq-φqid).
(4)
式(2)—(4)中:φ为磁链;ωr为转子角频率;u为电压;i为电流;L为电感;R为电阻;p为极对数;各符号用下标s表示定子,d表示直轴,q表示交轴,f表示励磁绕组,k表示阻尼绕组,m表示互感。
1.3 变流器
变流器包含电力电子开关,为强非线性系统,在一般仿真中,往往采用迭代法求解得到开关状态变化时刻[19]。然而这种求解方法较为费时,且难以通过FPGA编程实现。针对该问题,本文采用基于开关函数的直接求解方法。经测试,在仿真步长较小(开关频率100倍以上)时,具有工程上可接受的仿真精度(误差控制在2%以内)。
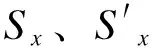
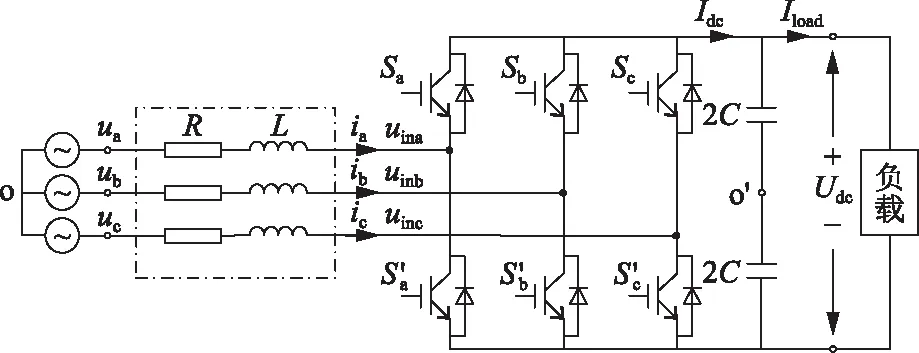
图3 三相两电平变流器Fig.3 Three-phase two-level converter
假设开关器件为理想开关,忽略零序分量,并定义如下开关函数:
(5)
根据基尔霍夫电压定律,可以得到三相静止坐标系下的交流侧开关模型如下:
(6)
式中uoo′为点o到点o′的电压降,对于三相无中线系统:
(7)
因此有:
(8)
对于直流侧,有如下关系:
(9)
如前所述,为了避免迭代运算,本文利用上一步的状态变量以及当前的开关信号来判断桥臂导通状态,从而得到换流器的直接求解方法。
1.4 变压器
风电机组机端变压器一般采用△-Y型式,因此不用考虑零序分量。为简单起见,采用两相静止坐标系下的T型等效电路,如图4所示,其中:R1、L1为原边电阻与漏感,Rm、Lm为励磁电阻与励磁电感,R′2、L′2为副边电阻与漏感(折算到原边),N为变比。

图4 变压器等效电路Fig.4 Equivalent circuit of a transformer
2 风电场模型
为了充分利用中央处理器(central processing unit,CPU)模型的修改便利性,以及FPGA模型的计算效率优势[15],考虑在机端母线处施加诺顿等效,风电机组部分在FPGA中求解,并通过等效电流源耦合到集电网络中,如图5所示,其中Z-1表示1个仿真步长的延时,下标n表示风电机组编号。
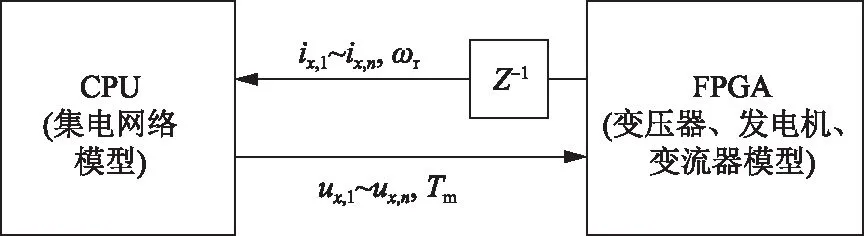
图5 风电场解算过程Fig.5 Diagram of wind farm computing
对于风电机组较多的情况,FPGA的完全并行化编程会耗费较多的资源。实际上由于一般具有确定的、远小于CPU的计算步长,FPGA模型还可以采用流水线技术(时间换空间)来实现多台风电机组在单个CPU步长内的串行求解。
图6所示为基于FPGA的风电机组流水线的求解过程,其中WT表示风电机组,tCPU为CPU计算步长,tFPGA为FPGA计算步长,假设每台风电机组计算时间为mtFPGA,且m≥n,ntFPGA 图6 风电机组流水线解算过程Fig.6 Diagram of pipeline computing of wind turbine 基于前述建模方法,在RT-LAB仿真平台中建立风电场的实时仿真模型,同时每台风电机组建立闭环控制器,控制器采用经典的双闭环矢量控制结构,其中内环控制电流,网侧外环控制直流电压与无功功率,机侧外环控制发电机转速。图7所示为仿真系统结构示意图,其中OP5600为CPU仿真机,OP5607为FPGA仿真机。 图8所示为风电场实时仿真模型。其中,CPU模型部分包含电网、场级变压器、线路、风电机组等效电流源以及风电机组控制器等,兼容SimPowerSystems模型,可以灵活修改风电场内部接线,仿真步长为20~50 μs。根据线路、变压器的数量不同,单个CPU计算核心可以仿真10~30台风电机组。 FPGA模型部分为风电机组仿真模型,采用浮点数计算模块建模,并预先生成bitstream文件,在实时仿真时加载,单个流水线设计为50级。1台风电机组的计算时间约为100时钟周期。因此,在200 MHz时钟频率条件下,1台风电机组的计算时间约为0.5 μs。 图7 实时仿真系统结构Fig.7 Diagram of real-time simulation system 图8 风电场实时仿真模型Fig.8 Real-time simulation model of a wind farm 由于1台OP5600机型最多可以使用16个CPU计算核心,上述2台仿真机(或1台新型的OP5700)能够满足包含数百台风电机组的风电场数字实时仿真需要。 为了验证模型的正确性,首先对单台风电机组进行并网运行仿真,并与基于Simulink/ SimPowerSystem (SPS)的仿真结果进行对比。机组参数如下:定子d、q轴自感分别为13.7 mH和11 mH,定子漏感1.14 mH,励磁绕组自感2.1 mH,阻尼绕组d、q轴自感分别为1.4 mH和1 mH,极对数2,直流电压1 200 V。 仿真结果如图9所示。在低速状态,由风轮带动发电机转动,不启动PWM控制;当转速超过1 200 r/min,启动PWM控制(载波频率1 080 Hz)。由此可以看到本文所提模型仿真结果与SPS模型仿真结果高度吻合,其中定子电流和电磁转矩误差基本控制在2%以内,且转速误差更小。 在RT-LAB中,通过分核处理,将一次回路和二次控制分置于不同的CPU核(各2个CPU核)。当采用40 μs仿真步长时,不断增加风电机组数量,观察仿真耗时,见表1。 由表2可以看出,随着风电机组数量增加,控制CPU的仿真耗时并没有增加,这主要是由于控制器采用了矢量化处理,1个模块同时处理数十台风电机组控制,即便没有接入风电机组,计算量仍然不变。控制CPU1的耗时较控制CPU2耗时大,这是由于控制CPU1中多了波形数据记录模块。主回路CPU的运算量随着风电机组数量的增加呈线性增加,这主要是将计算量大的电力电子与电机部分转移到FPGA中,而CPU中主要进行变压器 图9 单机启动仿真Fig.9 Start-up simulation of a single turbine 表1 风电场实时模型仿真耗时Tab.1 Time consumption of a wind farm real time model 与线路建模,在不考虑变压器磁饱和情况下基本上可以看作是线性电路,因此计算量随风电机组数量增加而线性增长。经实测,单个CPU核最多可以仿真25台风电机组的主回路,或者数十台风电机组控制器。 图10为风电场的启动过程仿真,其中包括公共接入(point of common connection,PCC)点交流电压、电流以及功率。该仿真算例中,50台直驱机组依次并网,并运行于1 MW、0.1 Mvar的工作点,最终PCC点输出有功功率50 MW,无功功率5 Mvar。 图10 风电场启动过程仿真Fig.10 Start-up simulation of a wind farm 基于上述详细模型,建立如图11所示的风电场,以考察交流故障情况下,不同位置风电机组的动态响应情况。其中机群1包含1号—3号风电机组,机群2包含4号—6号风电机组。风电机组通过2级升压并入220 kV电网。假设线路1和线路2缺省长度为20 km。 在某个时刻,假设3号风电机组变压器副边发生三相短路故障。2号、3号、4号机组的故障响应波形如图12—图14所示,其中给出了风电机组输入三相交流电压Ug,x、直流电压Udc、卸荷回路电流Ich、交流侧功率有功功率P与无功功率Q。 图12表明,2号风电机组距故障点的电气距离较近,交流电压跌落约50%,但由于故障时输入 图11 风电场启动过程仿真模型Fig.11 Start-up simulation model of a wind farm 风电功率较低,通过电流控制器的调节,仍然能够实现风电功率的稳定输出。 图13表明,3号风电机组距故障点电气距离最近,交流电压跌落幅度较大,风电功率难以输出,造成直流电压上升,并触发直流侧卸荷回路。 图14表明,4号风电机组距离故障点电气距离较远,交流电压没有明显变化,输出功率较为平稳。 图12 2号风电机组动态响应Fig.12 Dynamic response of No.2 wind turbine 图13 3号风电机组动态响应Fig.13 Dynamic response of No.3 wind turbine 图14 4号风电机组动态响应Fig.14 Dynamic response of No.4 wind turbine 本节在图11所示的风电场中,将各机组线路长度设为20 km,并研究PCC点处聚合模型与详细模型的不同阻抗特性。 图15所示为聚合模型仿真结果,即采用单台机组输出倍乘的方法模拟多台机组。图16所示为详细模型仿真结果。 由图15、图16可以看到,随着风电机组数量的增加,聚合模型的PCC点阻抗近似线性减小,而详细模型的PCC点阻抗特性呈现出更强的非线性,并预测到了内部线路可能引起的谐振峰(150 Hz附近),提示应进一步研究相关参数与控制设计。 图15 风电场阻抗特性(聚合模型)Fig.15 Impedance characteristics of wind farm (aggregation model) 图16 风电场阻抗特性(详细模型)Fig.16 Impedance characteristics of wind farm (detailed model) 基于数字实时仿真的半实物仿真是风电场控制保护系统研发、测试的有效手段,其中风电场建模是仿真测试的关键环节。相比于聚合模型,风电场详细模型能够保留风电场内部网络拓扑与动态特性,但往往耗费更多的计算资源。针对该问题,本文提出基于FPGA的风电场详细建模方法,利用模型分割与并行计算技术,实现不少于50台风电机组的高效求解。仿真结果表明: a)与SPS离线仿真模型相比,本文提出的基于FPGA的风电机组模型时域仿真结果的稳态误差控制在±2%以内。 b)使用2台RT-LAB仿真机就能完成包含数百台直驱风电机组的风电场实时仿真建模,其中风电机组的仿真步长不大于1 μs,集电系统仿真步长不大于50 μs。 c)风电场并网点阻抗特性与风电场内部接线以及并网风电机组数量间呈现出较为复杂的非线性关系,在研究大型风电场并网与控制问题时,有必要采用精细化的仿真模型。 综上所述,本文所提风电场电磁暂态实时仿真模型能够反映风电场内部拓扑结构以及各风电机组独立的动态特性,具有可调参数多、所需计算设备较少、成本较低等优点,适用于风电场精细化并网仿真以及风电场控制设备的半实物仿真测试。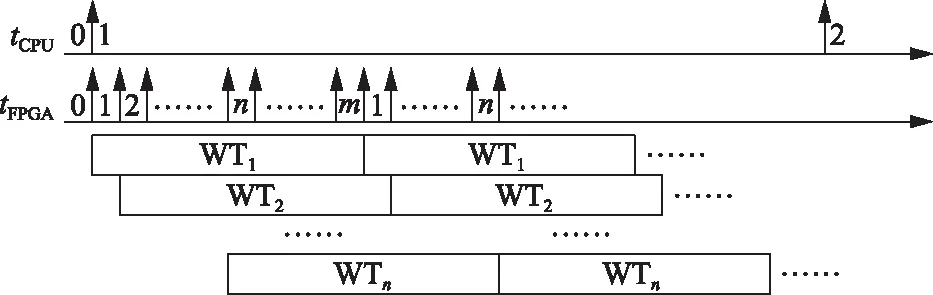
3 风电场实时仿真系统

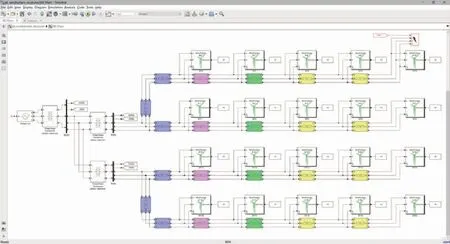
4 仿真验证
4.1 单机启动仿真
4.2 多机启动仿真


4.3 故障仿真

4.4 阻抗扫描

5 结论
