基于灰色马尔科夫模型的天津市供水总量预测

丁 祥， 王 彤

(1.长安大学基建处， 陕西 西安 710064; 2.长安大学 建筑工程学院， 陕西 西安 710061)

随着城市化的发展，水资源短缺的问题愈演愈烈，水资源的优化配置问题亟待解决，科学的预测供水量显得尤为重要。水量预测方法主要有人工神经网络法、灰色模型法、组合预测法等[1-6]。

灰色模型(Grey Model)是由邓聚龙[7-10]于1982年首次提出，当灰色模型GM(m,n)中只含有一个变量(m=1)且为一阶方程(n=1)时，灰色模型就被称为GM(1,1)模型。因为其具有建模过程简单、模型表达式简洁、便于求解等特点，已成功应用于农业、气象、环境和人口等领域[11]。由于模型自身具有缺陷，近年来很多学者对其进行了优化，优化方法大致可分为初始值优化、背景值构造函数优化等[12-13]。但是优化后的模型仍然不能很好地预测波动大、增长规律性不强或不规则变化的序列。有研究表明马尔科夫链中的转移概率矩阵能够很好地反应序列的波动性，有效弥补GM(1,1)模型的缺陷，故本研究联合两种数学方法构建灰色马尔科夫预测模型。

以天津市年供水总量预测为例，建立灰色马尔可夫预测模型，运用Matlab进行编程和求解。既突出GM(1,1)模型对时间序列模型需要数据少、预测结果精度高的优势，又结合马尔科夫链对波动性较大的数据预测精确的优点。

1 GM(1，1)模型与精度检验

设历史用水量序列为：

X(0)={X(0)(1)，X(0)(2)，…，X(0)(n)}

(1)

累加原始序列X(0)可得序列X(1)：

X(1)={X(1)(1)，X(1)(2)，…，X(1)(n)}

(2)

所以GM(1,1)模型的一阶微分方程可以写成：

(3)

式中a为系统的发展系数；u为系统的灰作用量。

按导数定义有：

(4)

将式(4)写成离散的形式：

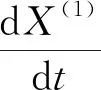
=X(1)(k+1)-X(1)(k)=X(0)(k+1)

(5)

对微分方程式(3)中X取k和k+1时刻的平均值，即：

(6)

则微分方程可变为：

X(0)(k+1)+a·Z(1)(k)=u

(7)

写成矩阵形式有：

(8)

令

(9)

则式(8)可表示为矩阵式：

Yn=BA

(10)

由式(10)可知，Yn和B是已知的，A为未知数。A中又有未知参数a和u，所以共有2个未知数，有n-1个方程。而n-1>2，故该方程组无解。通过最小二乘法可求得其近似解。将式(10)可变为：

Yn=B+E

(11)

式中E为误差项；为最小二乘估计值。

欲使：

min‖Yn-B‖2=min(Yn-B)T(Yn-B)

(12)

求得式(11)的最小二乘解为：

(13)

将上述解带入式(10)，可得:

(14)

写成离散形式为：

(15)

对生成的序列进行累减还原后得到：

(16)

X(0)(1)=X(1)(1)

(17)

式(16)和式(17)为GM(1,1)模型预测用水量的基本方程。

2 灰色马尔科夫预测模型

马尔可夫预测模型与灰色系统模型不同，它弥补了灰色预测模型的不足，可以对波动序列进行预测。将GM(1,1)模型与马尔可夫链理论相结合，建立灰色马尔科夫预测模型，模型建立步骤如下。

① 计算波动指数序列

(18)

② 划分状态

将波动指数序列划分为s个状态：

v(k)∈[ai,bi](i=1,2,…,s)

(19)

式中ai、bi分别表示第i个状态Ei的上限和下限，所以E=(E1，E2，…，Es)。

③ 初始概率矩阵

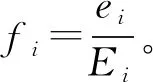
④ 状态转移概率矩阵

(20)

式中eij为从状态Ei经过一步转移为状态Ej的个数。

⑤ 状态转移矩阵

根据最大概率准则，预测结果所处状态应该是pi1,pi2,…,pin中最大者对应的状态，即当max{pij,pi2,…,pin}=pik时，就可以预测系统下一时刻将转向状态Ek，则Ek的中点或者均值表示预测数值。

若pik>pim(m=1,2,…,n；m≠k)且差值比较大时，则说明预测精度较高；若pik≈pim(m=1,2,…,n；m≠k)，则说明预测精度一般。

⑥ 计算预测序列

(21)

3 实例分析

3.1 研究区域选取

选择天津市作为研究区域，使用2001—2017年全市供水总量数据预测2018年全市供水总量，预测供水数据来源于《天津统计年鉴2019》。原始供水总量数据如表1所示。

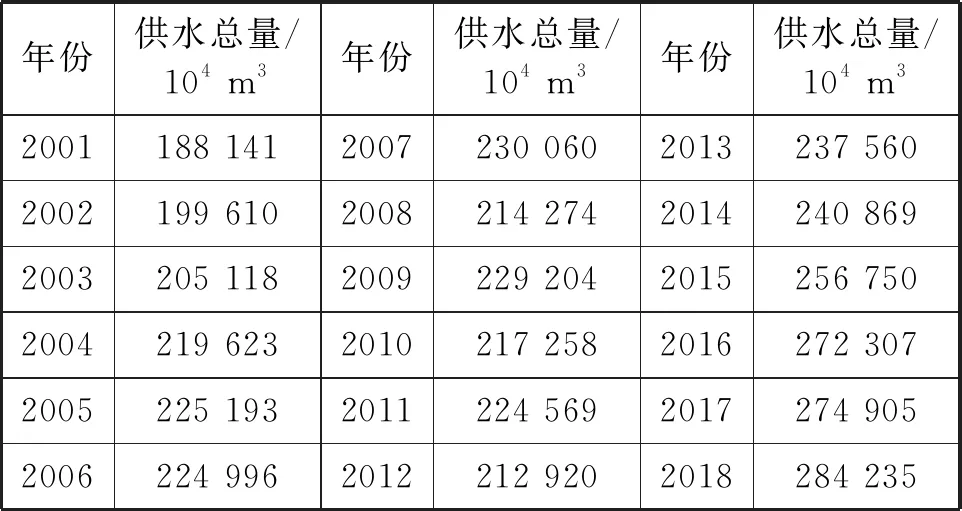
表1 天津市2001—2018年供水总量Tab.1 Total water supply quantity of Tianjin from 2001 to 2018

3.2 GM(1,1)供水量预测模型

建立原始供水总量序列为X(0)={188 141，199 610，205 118，…，274 905}，原始供水总量1-AGO序列X(1)={188 141，387 751，592 869，…，3 873 357}。

使用Matlab软件编程，采用最小二乘法，计算微分方程中X(0)(k+1)+aZ(1)(k)=u中的参数a=-0.018 56，u=1.950 59×105，带入得到微分方程表达式：X(1)(k+1)=188 141.001 051e0.018 56k-0.001 051。

求得2001—2017年供水总量的拟合值和相应的波动系数，如表2所示。

表2 GM(1,1)模型拟合结果和状态分布Tab.2 Fitting results and state distribution of the GM(1,1) model

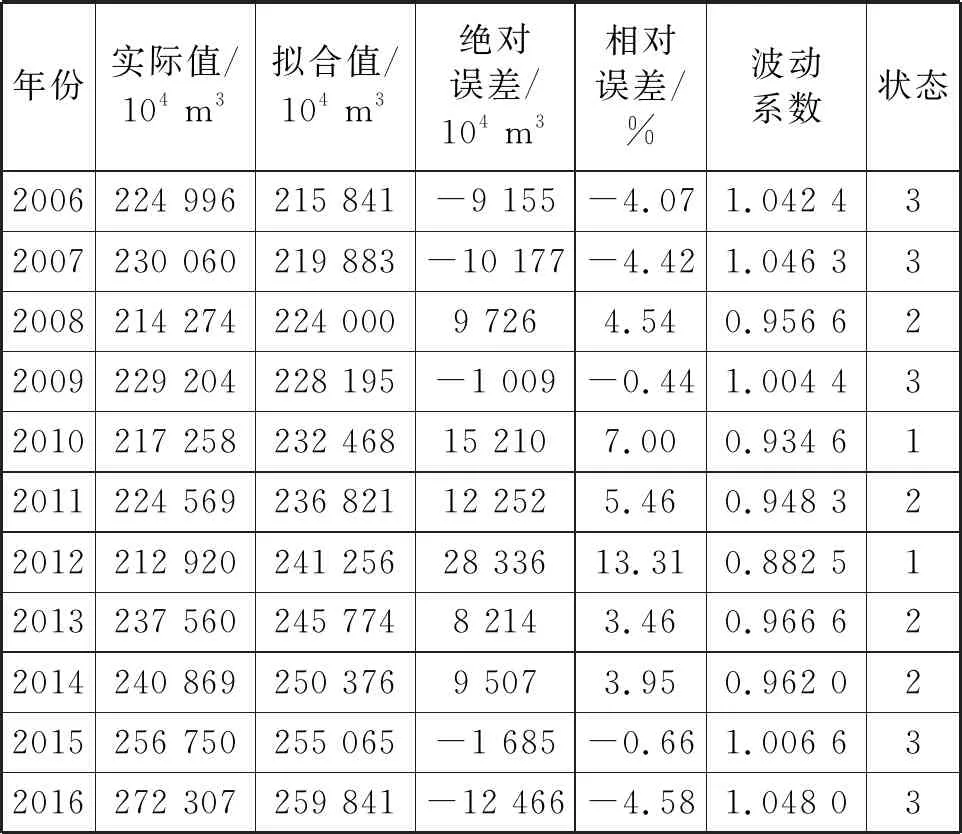
续表2 (Continue)

由式(16)可求得2017年供水总量拟合值为255 549×104m3。按照新陈代谢进化机制，去掉2001年供水总量数据，添加2017年供水总量数据，计算得到2018年供水总量拟合值为258 579×104m3。

3.3 灰色马尔可夫供水量预测模型

首先计算波动系数，结果见表2。波动系数最小值为0.9346，最大值为1.0629。采用等间距的状态划分方式，将波动系数划分为3个区间段。

E1：[0.882 5，0.942 6]

E2：[0.942 6，1.002 7]

E3：[1.002 7，1.062 9]

根据各年份供水量预测序列的波动系数进行状态划分，结果见表2。

得到初始概率：E1=2；E2=6；E3=8。

然后计算状态转移概率矩阵：M11=0；M12=2；M13=0；M21=1；M22=2；M23=3；M31=1；M32=1；M33=5。

因此，状态转移概率矩阵为：

预测2017年供水总量波动系数：2016年供水总量波动系数位于状态3，由max{p31，p32，p33}=5/7=p33可知2017年供水总量弹性系数位于状态3，数值等于状态3均值，即1.032 8。

预测2017年供水总量R2017=263 931×104m3，2018年供水总量R2018= 267 060×104m3。

3.4 模型精度检验与分析

3.4.1 GM(1,1)模型拟合性能

为了便于分析GM(1,1)模型拟合的精确性，绘制表2中的2001—2017年实际供水总量、拟合值和相对误差，如图1所示。

图1 GM(1,1)模型的拟合结果Fig.1 Fitting results of the GM(1,1) model

由图1可知，2001—2006年实际供水总量整体呈现上升趋势，但是在2007—2013年区间供水总量变化出现一定程度的波动。GM(1,1)模型拟合的供水总量变化曲线基本为一条上升直线，大致可认为是以固定速度逐年递增。在2001—2007年和2013—2016年两个实际供水总量递增区间，GM(1,1)模型拟合结果相对误差在±5%以内，拟合精度较高；在2007-2013年区间实际供水总量出现波动，拟合供水总量递增，GM(1,1)模型拟合结果相对误差大于±5%，其中2012年的相对误差更是高达13.31%。

以上结果表明，GM(1,1)模型对于均匀递增且无波动的序列拟合精度较高，对于波动较大序列拟合精度较低，不能满足使用需求，需要采取措施加以优化。

3.4.2 灰色马尔科夫模型预测结果分析

为更好地比较GM(1,1)模型和灰色马尔科夫模型，评价其预测精度，分别计算两个模型对2017年和2018年的供水总量预测的绝对误差、相对误差，结果如表3所示。

GM(1,1)模型的预测精度较低，相对误差绝对值大于7%。经过灰色马尔科夫链优化后的GM(1,1)模型预测精度得到大幅度提升，将相对误差绝对值控制在5%以内。GM(1,1)模型的预测值大幅度低于实际值，灰色马尔科夫模型在一定程度上起到了纠偏的作用，使得预测值偏离程度降低，但是预测值仍然低于实际值。

表3 GM(1,1)模型和灰色马尔科夫模型预测结果对比Tab.3 Comparison of the GM(1,1) and Grey Markov Model

4 结语

当采用GM(1,1)模型拟合波动比较大的数据时，误差会比较大，精度不够高。通过基于GM(1，1)的灰色马尔科夫模型的建立，原始序列波动可以在一定程度上由马尔科夫链通过转移概率来克服。以天津市2001—2018年供水总量为研究对象，拟合2001—2016年供水总量曲线、预测2017年及2018年供水总量，对比分析表明经马尔科夫链优化后的GM(1,1)模型预测精度满足要求，可应用于年供水量、用水量预测，为区域水资源配置优化提供参考。