薄厚度有机防护涂层的太赫兹无损检测与多元回归分析

涂婉丽， 钟舜聪， 罗曼婷， 徐轶群

(1.集美大学 轮机工程学院，福建 厦门 361021; 2.福建省船舶与海洋工程重点实验室，福建 厦门 361021;3．福州大学 机械工程及自动化学院，福建 福州 350108)

有机涂层的厚度对防护涂层性能有很大影响，间接对材料利用率和装备结构寿命起到重要作用，是涂层涂装过程中涂层质量监控与质量评价的一个关键参数[1]。近年来，研究人员采用脉冲太赫兹波成像技术(Terahertz Pulsed Imaging，TPI)开展多个领域的检测研究并推广应用[2-3]。而太赫兹对防护有机涂层的无损检测分析研究表明该检测方法具有广阔前景[4]。脉冲太赫兹波能够得到多层介质结构的层析图像，适合于检测涂层局部缺陷引起的介质结构变化；其能够检测分辨厚度在几十微米至几百微米量级的介质，适合工业中大部分覆有有机涂层的金属结构件；太赫兹成像系统检测信噪比较高，检测信息量大，能实现远距离探测；可以从时域信号及傅里叶变换频谱中选择任意一个数据点的振幅或相位进行成像和样品重构，能更好地表征含缺陷涂层结构的状态[5]。笔者之前已对脉冲太赫兹波检测有机防护涂层进行了数值模拟分析和实验研究，并提供了检测涂层厚度和缺陷的方法[6-7]。目前涂层喷涂过程中的在线监控还存在检测精度的问题，即喷涂前期薄厚度涂层的检测分辨。

相干长度与有效带宽和样品折射率的关系[8]为

Lc=c/(2nBW)

(1)

式中，Lc为相干长度；c为真空中的光速；n为样品折射率；BW为入射波的有效带宽。太赫兹检测介质的深度分辨率(即介质层最小检测厚度)受到太赫兹在介质中脉冲相干长度的限制。喷涂前期涂层厚度较小，用传统的“谐振峰寻峰法”难以直接检测获得[8]。主要原因体现在以下几方面：滤波反卷积受到滤波器截止频率等参数的限制，虽然能够去除大部分噪声，但同时也造成有用信息丢失，薄厚度涂层上下界面产生的微弱回波信号可能在滤波过程中随着噪声被截掉，难以满足薄厚度涂层的检测可靠性和精确性。目前，有研究人员采用太赫兹检测层状介质时，提出不进行反卷积操作而是直接对太赫兹检测信号直接进行处理，例如利用参数拟合构造理论回波法[9]、神经网络预测法[10]、最小方根差方法[11]等。本文针对喷涂前期的有机防护涂层厚度检测，对太赫兹检测信号进行不同方式预处理，提取特征参数建立多元回归模型，同时引入粒子群优化算法(Particle Swarm Optimization,PSO)进行分析，目的是更好地满足涂层喷涂过程的质量监控要求，提高太赫兹检测有机涂层厚度精度。

1 太赫兹检测有机防护涂层的信号及其预处理

笔者之前的研究工作已经验证了有限时域差分法(Finite-Difference Time-Domain，FDTD)能够分析脉冲太赫兹波在有机防护涂层系统中的传播和反射特性，与实验检测数据能较好吻合，并定量分析涂层结构[6-7]。本文提出的方法需要用到大量不同厚度涂层的数据，考虑到涂层喷涂成本，此处将采用太赫兹检测涂层的FDTD仿真信号。涂层样品结构采用 “防污涂料+防腐涂料+碳钢基体”形式：碳钢基体为半径20 mm、厚度0.2 mm的圆柱体，碳钢基体上覆有两层152 μm的Amercoat 235多功能环氧防腐涂料，折射率为1.74，接着涂上3层各127 μm的Interspeed 640无锡自抛光防污涂料，折射率为1.87。

在FDTD计算模型中，Yee网格尺寸大小为边长为0.03 mm的立方体网格，时间步长Δt=0.0577 ps；入射波形采用高斯脉冲，覆盖频率范围为0.1～1 THz，脉冲宽度设置为t0=34×Δt=1.9618 ps；太赫兹波垂直入射到检测介质表面，电场极化选择垂直极化；采用PML完全匹配层吸收边界；程序运行4096步以保证收敛。近区场传感器planar sensor设置在介质的横截断面位置，负责记录计算时间步内随时间变化的电场强度和磁场强度。因为实验中会不可避免地存在系统噪声等，所以在模拟的TPI检测信号中加入信噪比为32 dB的高斯白噪声。

此处将分别对防腐涂层和防污涂层进行检测分析。如图1所示，图1(a)和图1(b)分别是“防腐涂层+碳钢基体”涂层结构和“防污涂层+防腐涂层(厚度固定)+碳钢基体” 涂层结构的脉冲太赫兹波检测示意图。前者改变防腐涂层的厚度，每改变一次，则得到相应的涂层结构，进行一次FDTD仿真计算，每一次检测仿真中的参数都采用相同的设置(除了厚度参数外)，并采集和记录数据，其TPI检测信号如图2(a)所示。按照同样的方法，后者从小到大改变防污涂层的厚度，进行仿真计算，其TPI检测信号如图2(b)所示。其中，横轴为涂层检测时间，其余两轴分别是涂层厚度和电场强度。

从图2(a)中可以看出，由于空气-涂层介质间、防腐涂层-碳钢基体间的折射率差值较大，界面间产生较大反射峰。而从图2(b)中可以看出，由于防腐-防污涂料之间的折射率差值较小(前者为1.74，后者为1.87)，其界面间反射峰峰值明显较小。此外，不管是防腐涂层，还是防污涂层，随着涂层厚度的减少，其与其他介质层界面间的反射峰峰值持续减弱。这些弱峰值有时会埋没在系统噪声中，当进行反卷积时，常常随着噪声一起被过滤掉，因此不利于薄厚度涂层的检测。

1.1 TPI经傅里叶反卷积得到脉冲响应函数

傅里叶反卷积处理能够从太赫兹检测信号中得到脉冲响应函数，用来确定各介质层界面间回波脉冲的时间，经进一步计算可得到介质层的结构信息。此处针对不同厚度的涂层结构检测得到的TPI信号也经过反卷积操作得到相应的脉冲响应函数。其中的参考信号是通过将样品设置为金属介质而得到太赫兹检测反射脉冲，反卷积过程中采用了相同的滤波参数[6]。图3(a)、图3(b)是对应于图1(a)、图1(b)中两种不同有机防护涂层结构THz检测信号的脉冲响应函数。从图3(b)中可以看出，防污-防腐涂层界面间的反射非常小，特别是随着防污涂层厚度的减小，该特征更加难以分辨，这对定量分析薄厚度的防污涂层极为不利。主要原因是由于反卷积过程中的滤波在滤去噪声的同时也将信号的某些有用信息平滑掉了，降低了检测精度。

图1 两种不同防护涂层结构太赫兹检测示意图

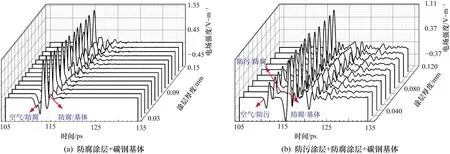
图2 FDTD仿真计算的TPI检测信号

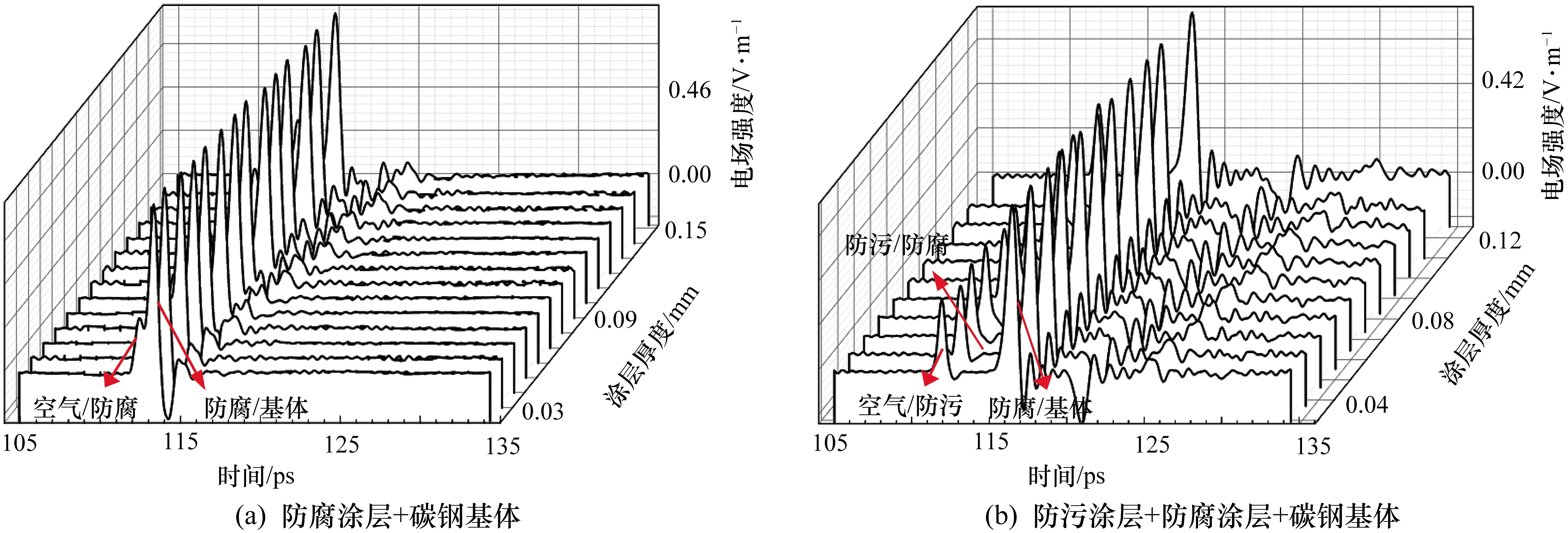
图3 两种不同有机防护涂层结构的THz检测信号的脉冲响应函数

1.2 TPI经小波变换得到细节系数

太赫兹检测多层介质结构时，不同介质界面间的反射峰会在信号中得到体现，信号的相位、频率和幅度会发生变化。小波变换目前已经在太赫兹检测系统测量时的信号处理中得到较多应用[12]。本文采用基于非抽样操作的平稳小波变换(Stationary Waveform Transform，SWT)来处理太赫兹原始检测信号。SWT可以提供丰富的时域特征信息和精确的频率局部化信息，且变换结果具有平移不变性，原始信号特征被分解在不同尺度的相同时域位置，有利于多层介质界面间反射峰特征的提取。如图4(a)、图4(b)是对应于图1(a)、图1(b)中两种不同有机防护涂层结构的TPI检测信号经过SWT变换的细节系数，其中小波系数选的是db1，分解层数为2。从图4中可以看出，涂层厚度的变化使得TPI检测信号的SWT细节系数也产生明显特征变化。可以看出SWT变换后的细节系数能够保留并凸显信号的特征，有利于进一步对薄厚度涂层预测分析处理时的特征提取与识别。

图4 两种不同有机防护涂层结构的THz检测信号的SWT细节系数

2 基于粒子群的多元回归分析方法

对实际问题中采集到的n组观测数据(xi1，xi2，…,xip，yi),i=1，2，…，n，理论回归方程如下：

E(y)=β0+β1x1+β2x2+…+βpxp

(2)

式中，p≥2；y为因变量(此处为所检测涂层的厚度)；x1，x2，…，xp为自变量(此处为信号经预处理后提取的参数)；β0，β1，…，βp为回归系数。

PSO算法是一种基于群体智能的优化算法[13]。本文利用PSO算法优化多元回归问题中的参数时，将回归模型的一组回归系数(β0，β1，…，βp)看作一个粒子，回归系数的个数p+1即为粒子维数。假设粒子群群体个数为M，则第i个粒子编码为：Pi=[βi0，βi1，…，βip]，i=1，2，…，M。种群中的每一个粒子代表模型估计问题中的一个候选解，回归系数的确定过程可看作从若干组候选解中选择最优化组合解的过程[14]。

具体步骤如下。

① 确定参数值：学习因子设为c1=c2= 2，作用是加速收敛且不宜陷入局部最优；粒子群个数M=100，最大迭代次数=300。

② 惯性权重w用于调节算法的全局与局部搜索能力之间的平衡，此处按照线性递减惯性权重策略(Linearly Decreasing Inertia Weight，LDW)进行更新[15]，公式为

(3)

式中，wmax为最大惯性权值，此处设为0.9；wmin为最小惯性权值，此处设为0.2；iter为当前迭代次数；itermax为总的迭代次数。

③ 初始化群体中的粒子，包括粒子的初始位置X和初始速度V，粒子的位置和速度均为p+1维的行向量。

④ 定义粒子适应度函数与目标函数。此处目标函数定义为实测值y与计算值y的残差平方和，相应的适应度函数ffitness定义为

ffitness=∑(y-β0-β1x1-β2x2-…-βpxp)2

(4)

目标函数值越小，粒子的适应度越小，粒子的位置越逼近最优解。

⑤ 计算每个粒子的适应度值，比较分析出更优解并更新全局极值gbest和局部极值pbest。

⑥ 更新各粒子的位置Vil和速度Xil：

Vil(t+1)=wVil(t)+c1×rand1×(pbestil(t)-Xil(t))+

c2×rand2×(gbestl(t)-Xil(t))

Xil(t+1)=Xil(t)+Vil(t+1)

1≤i≤M， 1≤l≤L

(5)

式中，rand1和rand2为(0，1)之间的随机数。为防止粒子远离搜索空间，粒子的每一维速度Vil都会限制在[-Vilmax,Vilmax]之间。

⑦ 计算优化目标函数，达到满足限定条件的目标函数值或达到设定的最大迭代次数时，即求得最优粒子每维的值，对应模型中的回归系数，算法结束；否则返回第⑤步。

3 涂层厚度的回归建模与预测结果分析

下面将对“防污涂料+防腐涂料+碳钢基体”有机防护涂层的太赫兹检测信号进行分析，建立基于PSO优化算法的涂层厚度多元回归分析模型。首先获得TPI检测不同涂层厚度的检测信号，并进行预处理分析，即选取TPI原始信号(加入高斯白噪声，信噪比为32 dB)、TPI脉冲响应函数、TPI信号的SWT细节系数(母小波选择db1，分解层数为2)；接着在上述几个预处理结果中提取适合的自变量，并建立不同参数下的多元回归模型，在其中引入PSO算法进行优化；最后用已建好的多元回归模型预测薄厚度涂层的厚度。

大量检测信号表明，涂层厚度与太赫兹检测信号中的以下几个参数存在非确定性相关关系：空气-涂层表面反射峰时间、涂层-碳钢基体界面反射峰时间、空气-涂层表面反射峰峰值和涂层-碳钢基体界面峰值。随着涂层厚度的变化，这几个参数也随之变化。即使对于比较薄厚度的涂层，从太赫兹检测信号中提取这几个特征参数也是比较容易的。因此本文的基于粒子群优化的多元回归分析方法中，在TPI检测信号及其预处理结果中分别提取上述4个参数作为自变量，依次为x1，x2，x3，x4，以涂层厚度作为因变量y，建立回归模型，则有

y=β0+β1x1+β2x2+β3x3+β4x4

(6)

每一次确定完回归系数和残差后得到的多元回归模型进一步被用来预测薄厚度涂层的厚度。将要预测的样本按照式(6)的方法要求，提取相应的自变量并代入所得到的回归模型，计算得到涂层厚度预测结果。回归分析过程采用Matlab程序完成。

此处采用回归模型拟合度判定系数R2作为判断标准[16]。

(7)

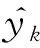
此外，还计算了均方根误差(Root Mean Square Error，RMSE)来评估预测的性能和精度，RMSE定义为

(8)

RMSE数值越小，说明预测精度越高。显然，RMSE与数据样本数量无关，更能反映模型的预测精度。

3.1 防腐涂层的厚度预测

为了对防腐涂层的厚度进行预测，在碳钢基体上涂覆一层折射率为1.74的Amercoat 235防腐涂层，改变涂层厚度，变化范围为20～152 μm，每改变一次就进行一次仿真计算，记录TPI模拟信号，取厚度在45～152 μm之间的65组数据(每间隔2 μm取一次数据)作为多元回归模型建立所需要的观测数据；取厚度在20～43 μm之间的13组数据作为需要预测的薄厚度涂层数据。防腐涂层厚度的回归分析及薄厚度涂层预测结果如表1所示。

3.2 防污涂层的厚度预测

为了对防污涂层的厚度进行预测，在碳钢基体上先涂覆厚度为304 μm、折射率为1.74的Amercoat 235防腐涂层，接着涂上一层折射率为1.87的防污涂层，厚度变化范围为20～127 μm，每改变一次就进行一次仿真计算，记录TPI模拟信号，取厚度在45～127 μm 之间的50组数据作为多元回归模型建立所需要的观测数据；取厚度在20～43 μm之间的13组数据(每间隔2 μm取一次数据)作为需要预测的薄厚度涂层数据。防污涂层厚度的回归分析及薄厚度涂层预测结果如表2所示。

表1 防腐涂层厚度的回归模型分析及其预测结果对比

表2 防污涂层厚度的回归模型分析及其预测结果对比

从表1、表2可以看出，不管是防腐涂层还是防污涂层的分析，并且不论是采用TPI原始信号、TPI脉冲响应函数还是TPI信号的SWT细节系数作为分析对象，均可以得到下列结论：本文中引入PSO算法的多元回归分析用于预测薄厚度涂层时，预测精度比较高，体现在均方根误差RMSE数值较小；这说明粒子群优化在多元线性回归分析的参数估计问题中起到了积极作用，回归速度更快。此外，采用TPI原始信号进行分析得到的薄厚度涂层预测精度最低，原因可能是原始信号中的噪声影响了信号有用信息的分辨。而即使SWT细节系数分析时回归模型的拟合度R2不如脉冲响应函数(如防腐涂层分析时的0.9519小于0.9696，防污涂层分析时的0.9372小于0.9671)，但薄厚度涂层的预测精度却高于后者(如防腐涂层分析时的RMSE为0.0081小于0.087，防污涂层分析时的RMSE为0.0079小于0.0088)，说明SWT细节系数有利于涂层结构的特征提取与识别，提取参数后可得到较好的多元回归模型和预测精度。

4 结束语

本文在多元线性回归分析问题中引入PSO算法，分别采用TPI检测信号及其不同预处理结果进行参数提取作为回归自变量，建立不同的回归模型，并用以预测薄厚度涂层。结果证明了PSO算法在多元线性回归分析的参数估计问题中是有效且可行的。以TPI信号的SWT 细节系数作为参数提取的分析对象时，薄厚度涂层预测结果均好于其他TPI信号预处理结果的分析。可见，多元回归分析结合平稳小波分析将有助于工业喷涂时提高薄厚度涂层的检测精度。