基于导波能量特征PCA的结冰定量检测方法研究

周世圆， 赵明华， 胡晓丹， 于全朋， 徐春广

(北京理工大学 机械与车辆学院，北京 100081)

飞机在飞行过程中，当温度较低时，飞机表面与云层发生碰撞，使得过冷水迅速发生相变，导致在飞机的许多部件上结冰[1]。飞机结冰会造成飞机质量增加，飞行阻力增大，影响飞机的气动性能、操作稳定性和起降特性，严重降低飞机飞行的安全性，甚至导致飞行事故的发生[2]。因此，及时检测和清除飞机表面上的结冰对于飞行安全非常重要。结冰检测是除冰系统工作的基础，可靠的结冰检测对于后续的除冰是至关重要的。

针对飞机结冰检测，研究人员提出了许多方法。Jarvinen[3]研究了通过测量阻抗、热导率和温度变化来检测飞机上是否存在结冰并确定其厚度的方法。Zhuge等[4]提出了基于近红外图像处理技术的飞机机翼结冰检测方法。Zou等[5]研究了使用倾斜端面光纤技术检测结冰类型的方法。Ikiades等[6]研究了通过测量散射和反射光强度确定机翼结冰厚度和类型的方法。Liu等[7]应用超声脉冲回波法测量频率相关衰减系数，进而对结冰类型进行表征。Schlegl等[8]基于空气、水和冰之间的电特性差异对飞机表面结冰进行检测。然而，这些方法只能在一个点或一个小区域内探测结冰。对于飞机表面结冰，这些方法需要大量的分布式传感器，实际上未在飞机结冰检测中得到很好的应用。

近年来，超声导波方法因其具有高灵敏度和大面积检测能力而受到了许多研究人员的关注和研究。Vellekoop等[9]研究了基于Love波的结冰检测方法，能够测量1～1.5 mm厚度的结冰。Gao和Rose[10]将铝层和冰层视为两层结构，对SH波传播进行建模，通过分析结冰的频散曲线来检测和分类结冰。Mlyniec等[11]研究表明铝板中A0模态导波幅值和S0模态导波飞行时间可以用于结冰检测。Zhao和Rose[12]通过结合Lamb波和概率重构算法，对结冰进行成像。赵伟伟等[13]基于椭圆定位算法研究了不同压电片布局对导波结冰检测成像质量的影响。

现有的导波检测方法大多是对结冰进行定性检测和分类，对结冰进行定量检测的研究较少，因此很难在结冰初期探测到结冰，无法及时启动除冰系统去除结冰，给飞机飞行带来一定安全隐患。结冰定量检测较难实现的主要原因是超声导波具有多模态特性和频散特性，结冰探测中导波信号波形较为复杂，给信号识别尤其是定量检测带来极大挑战。飞机的机翼是常见的结冰部位，通常机翼蒙皮材料为铝，为解决飞机结冰定量检测难题，尽早发现飞机初期结冰，本文采用铝板作为基底材料，采集结冰探测导波信号，提取导波信号多个特征，利用主成分分析(Principal Component Analysis,PCA)方法处理导波信号特征，获得导波信号综合得分，并建立综合得分与结冰长度(结冰区域沿导波传播方向尺寸)的关系，在结冰检测时计算导波信号综合得分，依据综合得分与结冰长度的关系对铝板上结冰长度进行定量检测。通过仿真实验和实测实验验证了该方法的可行性和可靠性。

1 结冰长度定量检测PCA方法

PCA是一种通过降维技术把多个变量转化为少数几个主成分的统计方法，是基于降维思想产生的处理高维数据的方法[14]。PCA的主要目的是用较少的特征去解释原来数据，将相关性很高的特征转化成彼此相互独立或不相关的特征[15]。主成分综合得分可以作为表征数据的综合性指标。

对于一组数据，共有n个样本，每个样本有p项评价指标，构成一个n×p阶矩阵，

(1)

式中,xj=[x1j,x2j,…,xnj]T，j=1,2,…,p。PCA就是将p个观测变量综合成p个新的综合变量，即主成分：

(2)

由于每个主成分的方差是递减的，包含的信息量也是递减的，所以实际分析时，一般不是选取p个主成分，而是根据各个主成分累积贡献率的大小选取前m个主成分。根据学者Jolliffe的研究，一般累积贡献率达到85%以上，可保证综合变量包括原始变量的绝大部分信息[16]。要求累积贡献率达到95%，以利于更好地保留原始变量的信息。

超声导波检测结冰时，由于导波信号复杂，采用多信号特征取代单信号特征进行检测可提高检测精度与可靠性。但由于信号各特征之间存在相关性，过多的特征会增加分析问题的难度与复杂性。因此考虑使用一个综合特征对信号进行描述，从而得到结冰长度与该综合特征的关系。PCA方法可以通过降维技术把多个变量转化为少数几个主成分，也容易根据主成分获得综合得分，从而获得上述的“关系”。因此，采用PCA方法对导波信号特征进行降维，获得信号特征主成分综合得分，主成分综合得分与结冰长度有对应关系，以此来对结冰长度进行定量检测。

综上所述，结冰长度定量检测PCA的步骤流程如图1所示。首先，提取导波信号特征，构建信号特征矩阵。由于各信号特征量级相差较大，采用Z标准化方法对数据进行标准化处理。Z标准化方法是最常用的标准化方法之一，将一组数据分别减去均值，除以标准差，标准化后的数据均值为0、方差为1[17]。然后计算标准化各特征之间的相关系数，构建相关系数矩阵，并通过雅可比方法求解矩阵特征值和特征向量。再根据累积贡献率确定主成分个数，贡献率为该主成分特征值占全部特征值总和的比例，累积贡献率为贡献率的累加和。确定主成分个数后，以特征值对应的特征向量为权值，对各标准化特征进行加权计算得到主成分，再以主成分贡献率为权值，对各主成分进行加权计算得到综合得分。最后，建立综合得分与结冰长度的关系，依据此关系进行结冰检测。

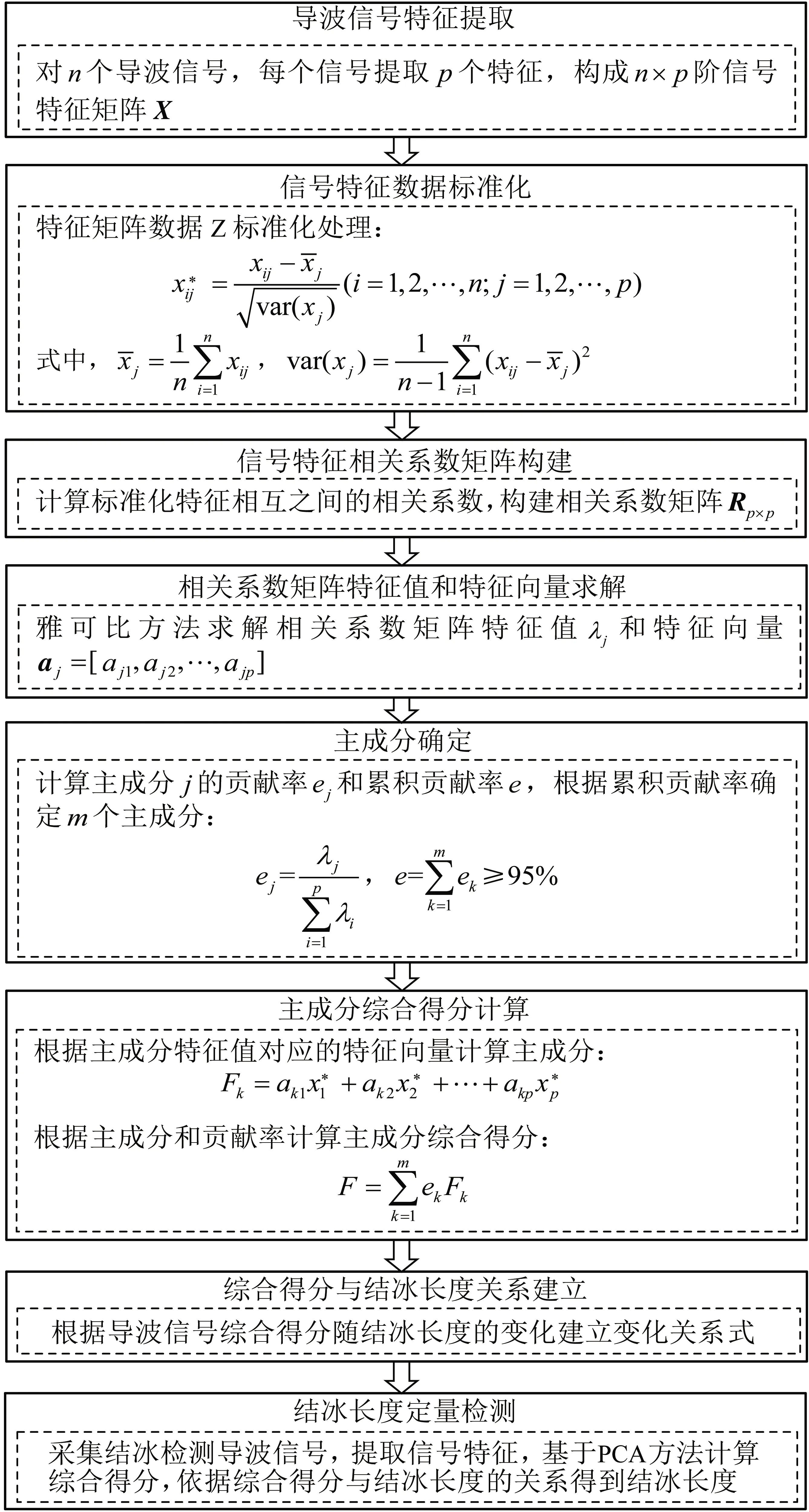
图1 结冰长度定量检测PCA步骤流程

2 结冰长度定量检测仿真实验

为验证利用结冰探测导波信号主成分综合得分测量结冰长度的可行性，对结冰铝板结构进行有限元仿真，获得多个结冰长度导波信号时域和时频域特征，基于PCA方法对多信号特征进行分析，采用综合得分对结冰长度进行评价。

2.1 仿真模型建立

在COMSOL中分别建立铝板和结冰铝板二维时域仿真模型，如图2所示，选择固体力学物理场进行分析。铝板尺寸为160 mm×1 mm，材料选用COMSOL的内置材料Aluminum，杨氏模量为70 GPa，泊松比为0.33，密度为2700 kg/m3。结冰厚度为1 mm，长度分别为5 mm、10 mm、15 mm、20 mm、25 mm、30 mm、35 mm和40 mm，冰的类型为明冰[12]，杨氏模量为8.3 GPa，泊松比为0.35，密度为900 kg/m3。模型两端面为低反射边界，模型左端垂直于斜楔加载位移载荷，采用加汉宁窗的5个周期正弦信号激励产生S0模态导波，中心频率为2.5 MHz，在距离左端面100 mm处接收导波信号。网格剖分采用自由三角形网格，并且保证在1个波长范围内至少包含8个网格。

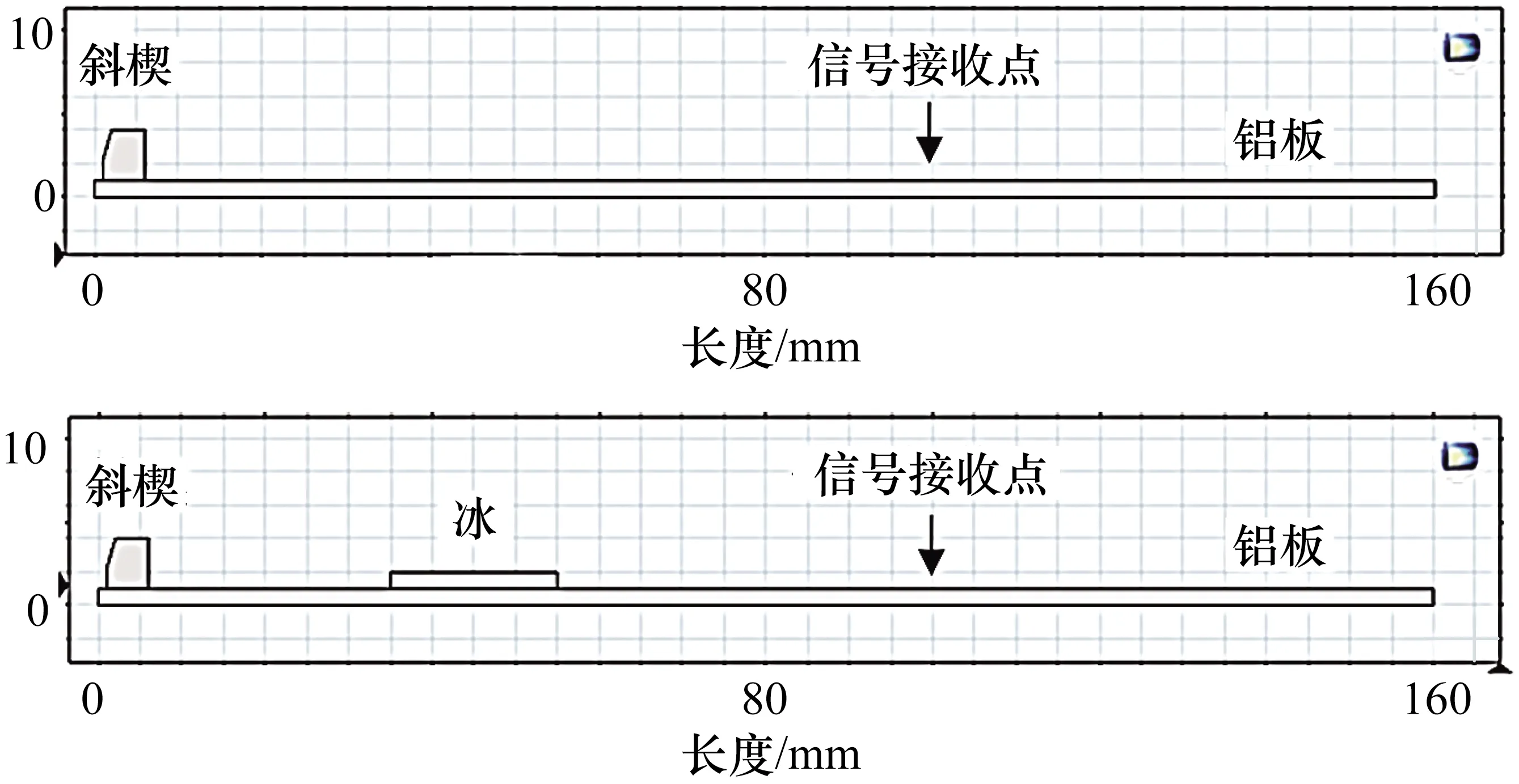
图2 铝板和结冰铝板仿真模型

2.2 仿真数据分析

在不同结冰长度下进行仿真，采集的导波信号如图3所示。由图3可知，信号幅值随结冰长度的增加明显减小，时域能量特征变化显著，主要原因是导波从铝板进入冰层，会发生反射、透射与折射，损失部分能量。因此，提取信号均方根值、标准差、绝对均值、方根幅值、峰峰值、波形因子、峰值因子、脉冲因子、裕度因子和峭度共10个与能量相关的时域特征。

结冰还会导致铝板刚度、阻尼和结构固有频率等发生变化，影响导波信号的频率成分，使不同结冰长度下的各频带能量不同。为了分析结冰长度对导波信号各频带能量的影响，选择db8小波基函数对导波信号进行3层小波包分解，得到各频带能量如图4所示，从图4中可以看出，频带2和频带4能量较高，其余频带能量接近于0，并且在结冰长度不同时，这2个频带能量变化较明显。因此，提取这2个频带能量，作为时频域特征。综上，对导波信号共提取12个特征参数，如表1所示。

对提取的信号特征进行PCA，首先对数据进行标准化处理，用Zi(i=1,2,…,12)表示标准化后的12个特征参数，结果如表2所示。对标准化后的特征参数，计算两两之间的相关系数，构成相关系数矩阵，用雅可比方法求解相关系数矩阵的特征值和特征向量，并按λ1>λ2>…>λ12排列，计算主成分的贡献率和累积贡献率，如表3所示。主成分1和主成分2的贡献率分别为89.515%和9.929%，累积贡献率达到99.444%。根据累积贡献率e≥95%能够较好地解释原始数据，确定2个主成分，并使用主成分1和主成分2计算综合得分，对结冰长度进行评价。根据主成分特征值对应的特征向量得到主成分F1和F2表达式:

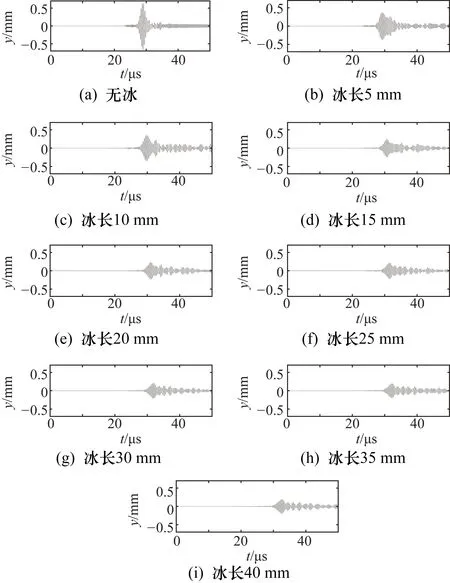
图3 不同结冰长度仿真信号

F1=0.2984×Z1+0.2984×Z2+0.2664×Z3+0.2511×Z4+

0.3045×Z5+0.2868×Z6+0.2874×Z7+0.2877×Z8+

0.2880×Z9+0.2877×Z10+0.3030×Z11+0.2996×Z12

(3)

F2=0.1860×Z1+0.1860×Z2+0.4453×Z3+0.5168×Z4-

0.0513×Z5-0.2914×Z6-0.2721×Z7-0.3033×Z8-

0.3015×Z9-0.2914×Z10+0.1008×Z11+0.1549×Z12

(4)

根据主成分和贡献率得到综合得分F表达式:

F=0.89515×F1+0.09929×F2

(5)

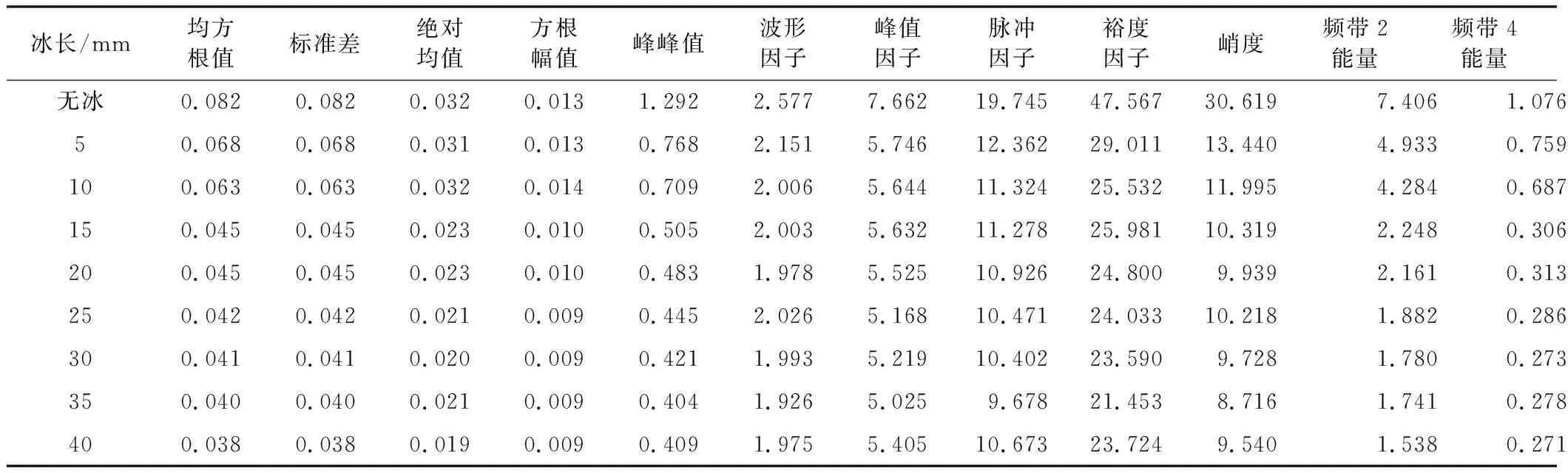
表1 仿真信号特征参数

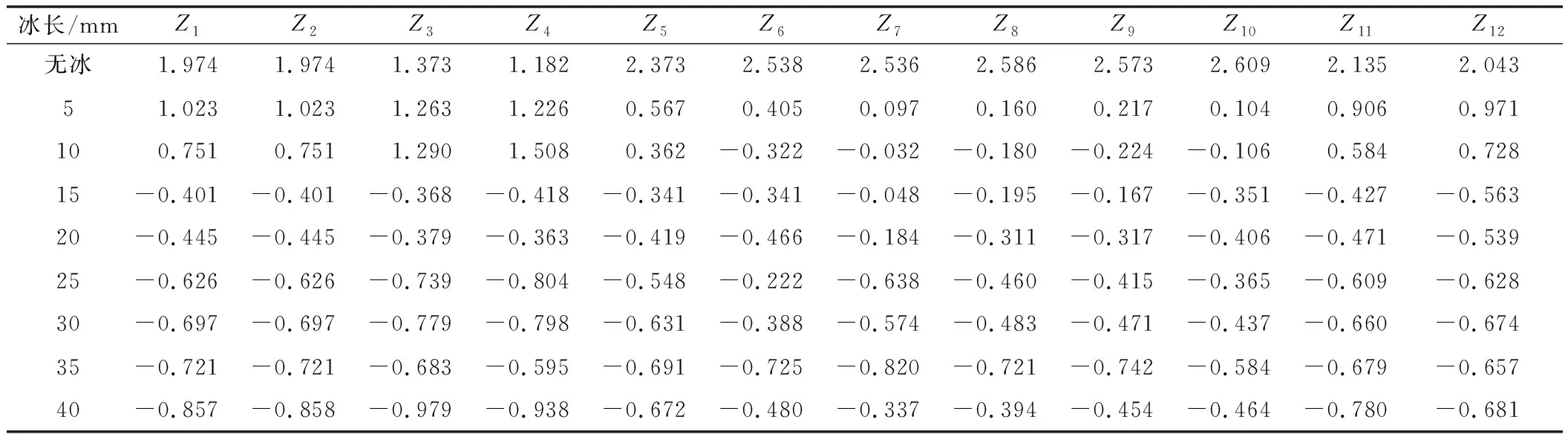
表2 标准化仿真信号特征参数

表3 主成分贡献率和累积贡献率(仿真)

经过计算得到综合得分F随结冰长度的变化关系如图5所示。从图5中可以看出，随着结冰长度的增加，利用提取的结冰探测导波信号特征，基于PCA获得的综合得分逐渐减小。根据此关系曲线，通过计算未知长度结冰探测导波信号综合得分，可以得到结冰长度。仿真实验验证了利用PCA方法处理结冰探测导波信号和定量检测结冰长度的可行性。

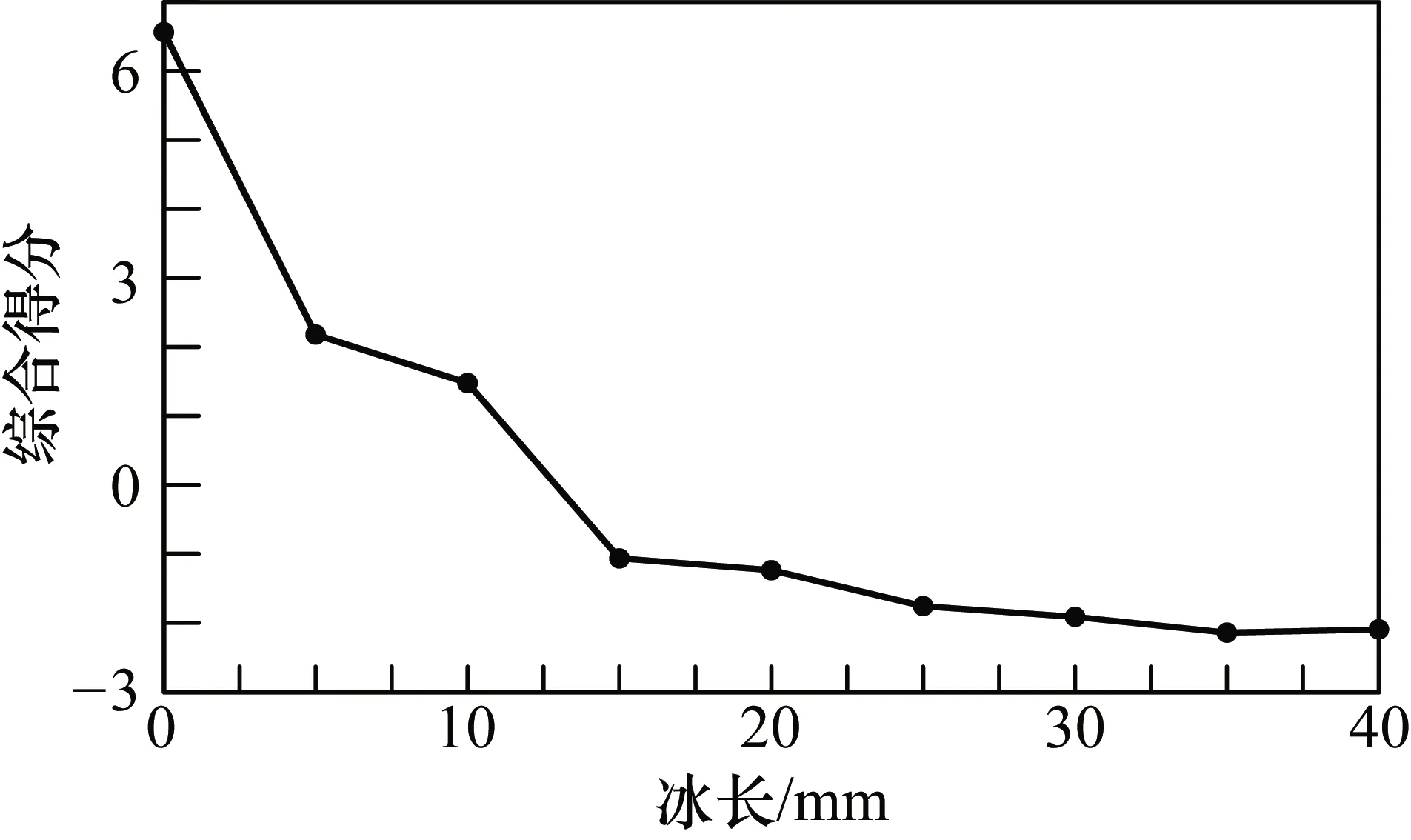
图5 综合得分随结冰长度变化关系

3 结冰长度定量检测实验验证

为进一步验证利用结冰探测导波信号主成分综合得分测量结冰长度的可行性，搭建结冰探测实验系统，开展不同长度结冰探测实验，基于上述PCA方法对结冰探测导波信号进行分析，建立综合得分与结冰长度的关系。进而对预制结冰区域开展结冰长度定量检测验证实验，验证PCA方法的有效性和可靠性。

3.1 实验系统组成

实验系统如图6所示，包括导波检测系统、结冰铝板、换能器、斜楔和冰箱。被测铝板尺寸为300 mm×300 mm×3 mm，采用斜入射换能器一发一收的形式进行结冰探测，激励S0模态导波，激励的中心频率为2.5 MHz。在铝板上设置7个结冰区域，如图7所示，冰的厚度为1 mm、宽度为20 mm，长度分别为5 mm、10 mm、15 mm、20 mm、25 mm、30 mm、40 mm。

3.2 综合得分与结冰长度关系建立

首先采集铝板上无冰时的导波信号，然后采集铝板上冰长分别为10 mm、20 mm、30 mm、40 mm时的导波信号。采集的5个导波信号如图8所示，由图8可知，信号的幅值随结冰尺寸的增加明显减小，时域能量特征变化显著。根据上述信号特征提取方法，提取导波信号10个与信号能量相关的时域特征和2个与能量相关的时频域特征，共12个特征参数，如表4所示。

图6 结冰探测实验系统

图7 结冰区域示意图

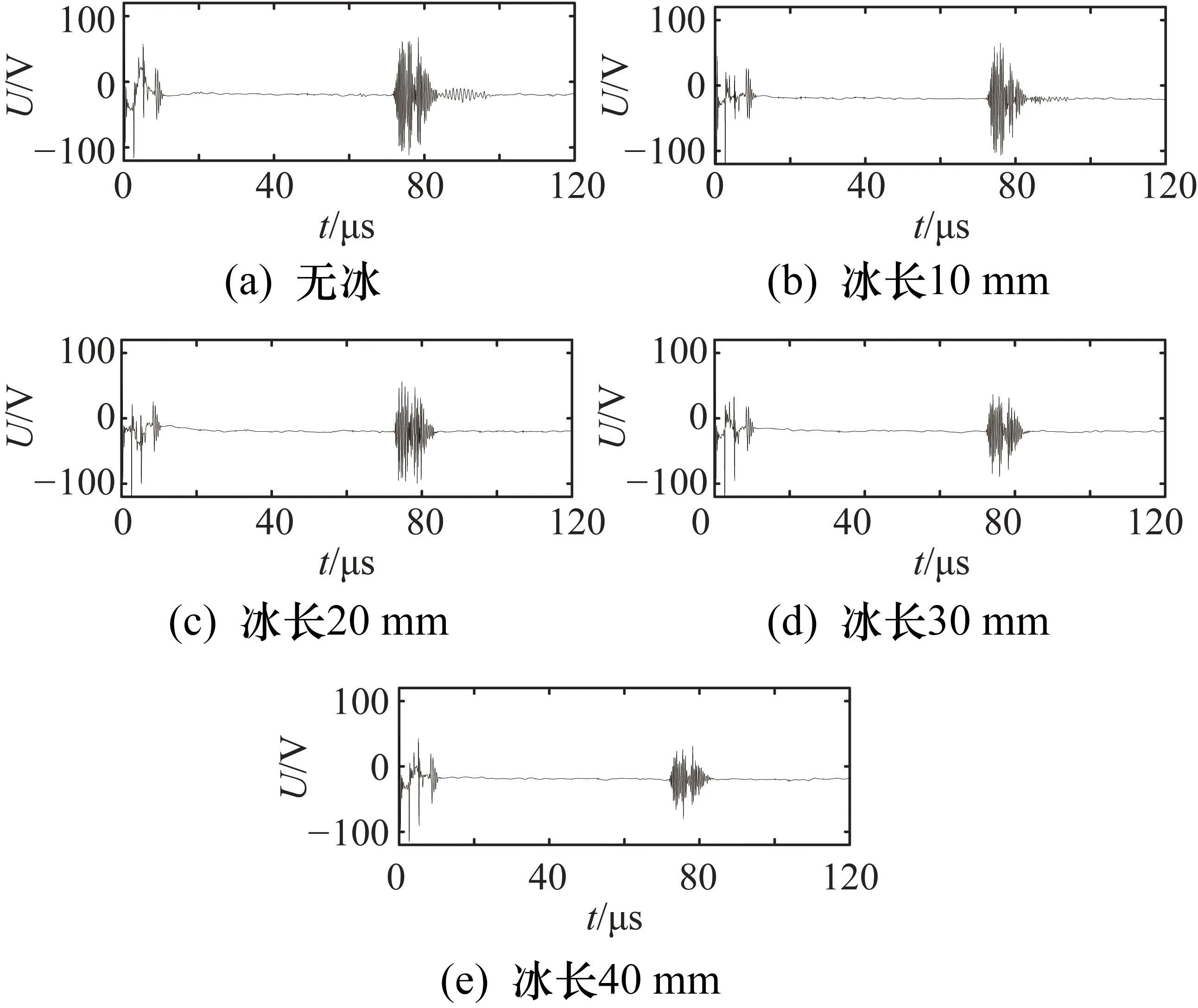
图8 不同结冰长度实验信号

用Zi(i=1,2,…,12)表示标准化后的12个特征参数，对数据进行标准化处理的结果如表5所示。计算标准化后的数据两两之间的相关系数，构成相关系数矩阵，并求解矩阵的特征值和特征向量，计算得到主成分1和主成分2的贡献率分别为85.273%和11.192%，累积贡献率达到96.465%，如表6所示。根据累积贡献率e≥95%确定2个主成分，使用这2个主成分计算综合得分，对结冰长度进行评价，主成分F1、F2及综合得分F的表达式为

F1=0.3120×Z1+0.3102×Z2+0.2944×Z3+0.2734×Z4+

0.3122×Z5+0.3020×Z6+0.3123×Z7+0.3123×Z8+

0.3123×Z9-0.0485×Z10+0.2928×Z11+0.2750×Z12

(6)

表4 实验信号特征参数

表5 标准化实验信号特征参数

表6 主成分贡献率和累积贡献率(实验)

F2=0.0485×Z1-0.0948×Z2+0.2573×Z3+0.3764×Z4+

0.0076×Z5-0.1944×Z6+0.0165×Z7-0.0121×Z8-

0.0211×Z9+0.8334×Z10-0.2180×Z11+0.0052×Z12

(7)

F=0.85273×F1+0.11192×F2

(8)

经过计算得到综合得分F随结冰长度的变化关系如图9所示。从图9中可以看出，随着结冰长度的增加，基于PCA获得的综合得分逐渐减小，采用线性回归进行拟合，表达式为

y=-0.1703x+3.4061

(9)

式中，y为综合得分;x为结冰长度。拟合优度R2=0.9732，拟合效果较好，说明主成分综合得分与结冰长度具有良好的线性关系，进一步验证了利用导波信号主成分综合得分测量结冰长度的可行性。在结冰检测时，激励并接收导波信号，提取所接收导波信号的能量特征，采用PCA法对导波信号能量特征进行处理并计算综合得分，根据综合得分与结冰长度的对应关系，可以获得结冰长度。

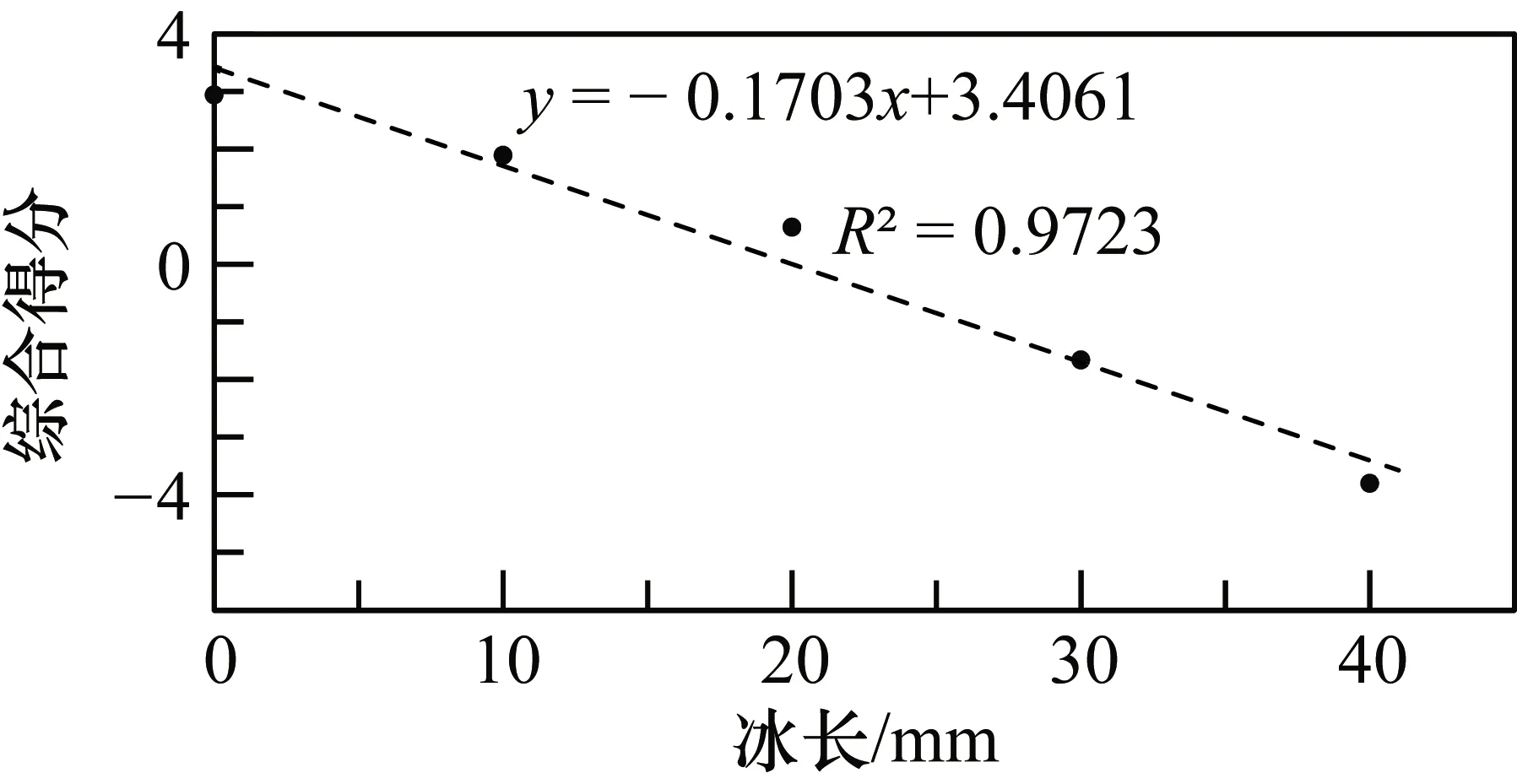
图9 综合得分随结冰长度变化关系

3.3 结冰长度定量检测实验验证

为验证基于导波能量特征PCA的结冰定量检测方法的有效性，以预制的结冰长度分别为5 mm、15 mm和25 mm的结冰区域为例进行验证，采集的结冰检测导波信号如图10所示。提取信号能量特征，并进行标准化处理，如表7所示。代入式(6)～式(8)计算得到其能量特征主成分综合得分分别为2.5318、0.9762和-0.6532。根据综合得分与结冰长度的关系式(9)，计算得到结冰长度分别为5.14 mm、14.27 mm和23.84 mm，与实际结冰长度误差较小，证明了基于导波能量特征PCA的结冰长度定量检测方法的有效性。

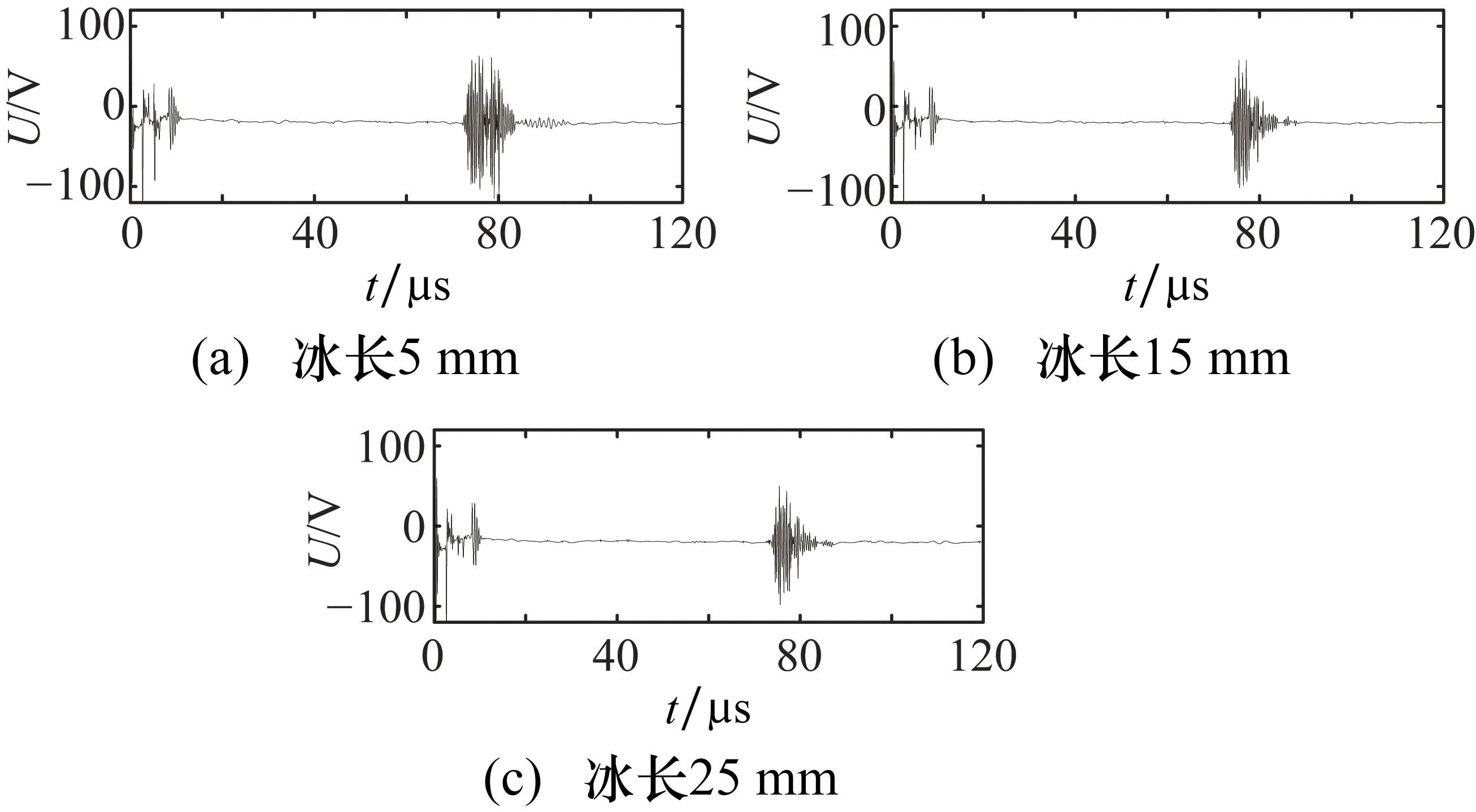
图10 结冰长度定量检测验证实验信号

表7 标准化验证实验信号特征参数

此外，采用传统的信号能量分析法(信号幅值平方和)对上述铝板上无冰和冰长分别为10 mm、20 mm、30 mm、40 mm时的导波信号进行了处理，得到导波信号能量随结冰长度的变化关系如图11所示。从图11中可以看出，信号能量随结冰长度的增大而减小，采用线性回归进行拟合，表达式为,

y=-7420x+692669

(10)

式中，y为信号能量;x为结冰长度;拟合优度R2=0.9949。以上述预制的结冰长度分别为5 mm、15 mm和25 mm的结冰检测导波信号进行验证，计算得到信号能量分别为683583、542848和479732，代入式(10)计算得到结冰长度分别为1.22 mm、20.19 mm和28.70 mm，与实际结冰长度误差较大。

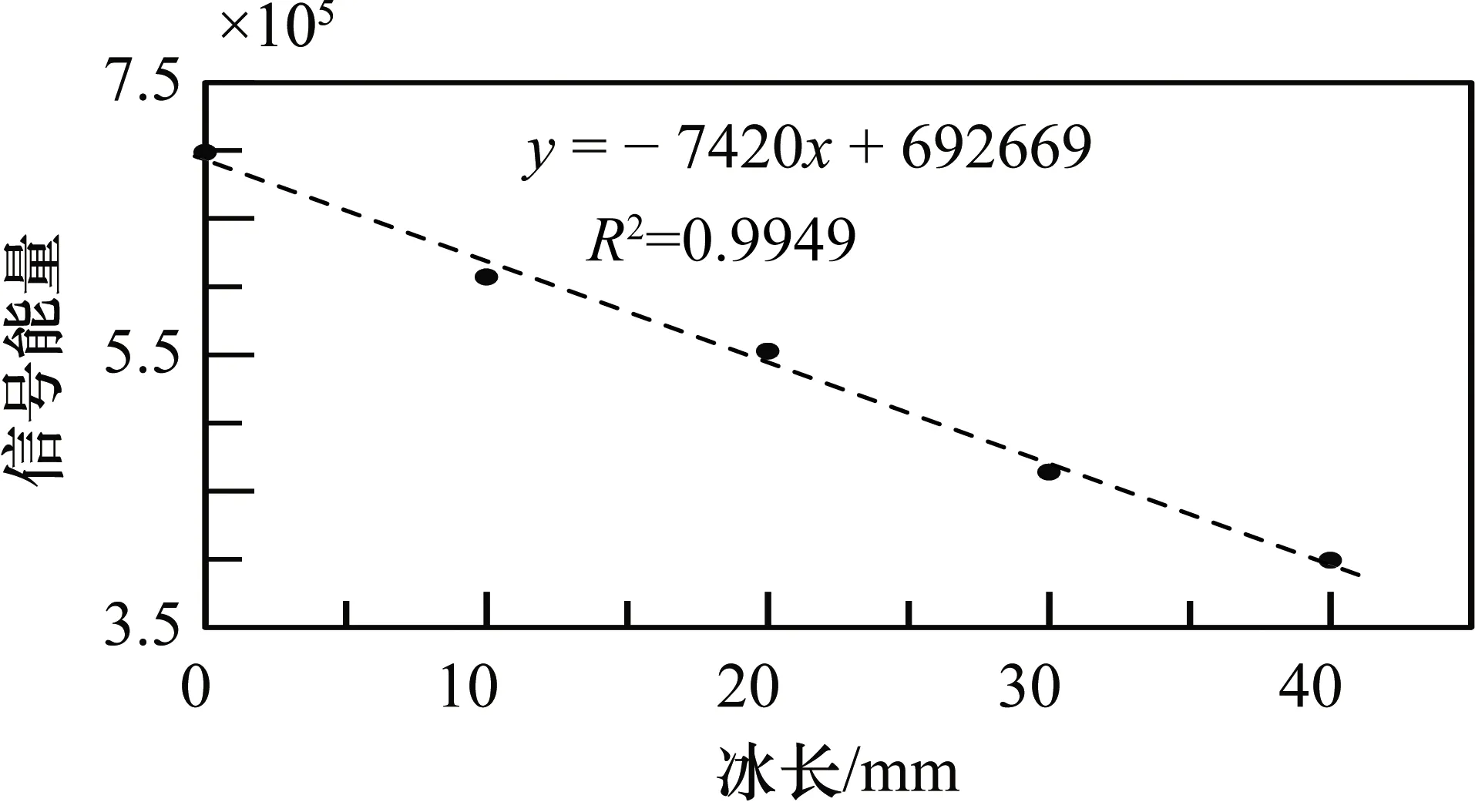
图11 信号能量随结冰长度变化关系

两种方法的检测结果如图12所示，由图12可知，PCA法的检测值更接近于实际值。检测结果对比如表8所示，PCA法对预制5 mm、15 mm和25 mm冰长结冰的检测误差分别为2.8%、4.9%和4.6%，而传统能量法的检测误差为75.6%、34.6%和14.8%。PCA法的检测误差较小，检测精度明显高于传统的能量法。并且在结冰长度较小时，传统能量法的检测误差非常大，基本无法进行定量检测，而PCA法在结冰长度较小时仍有较高的检测精度。因此，PCA法更适用于结冰长度的定量检测，对飞机初期结冰有更好的检测能力。

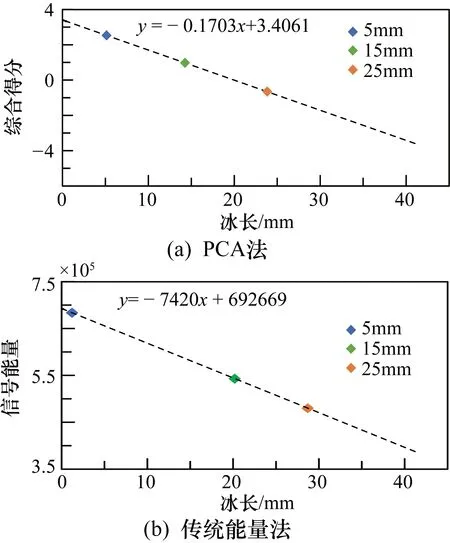
图12 结冰长度定量检测结果

表8 结冰长度定量检测结果对比

4 结束语

提出了基于导波能量特征PCA的结冰定量检测方法，通过仿真实验对铝板结冰进行了探测，提取了导波信号时域和时频域中与能量相关的特征，利用PCA方法对导波信号特征进行降维，获得了信号主成分综合得分与结冰长度的关系，即随着结冰长度的增加，信号特征的综合得分逐渐减小，验证了利用信号主成分综合得分检测结冰长度的可行性。并采用上述方法进行实测实验，实验结果表明主成分综合得分与结冰长度具有良好的线性关系，并建立了综合得分与结冰长度的变化关系式。对预制结冰区域的结冰长度定量检测结果表明PCA法的检测误差较小，检测精度高于传统的能量法，尤其是在结冰长度较小时，PCA法的优势更为突出。该方法对小尺寸结冰的探测能力较强，能够用于飞机初期结冰的探测，从而在结冰初期启动除冰系统，保证飞机飞行的安全性。

在结冰宽度和厚度一定的条件下实现了结冰长度的定量检测，但未分析结冰宽度和厚度对导波信号综合得分的影响，对结冰尺寸的检测不完善。因此，下一步工作的重点是研究结冰宽度和厚度对导波信号综合得分的影响，建立结冰尺寸与综合得分的关系，实现结冰尺寸或体积的定量检测。