路网-电网结合的电动汽车两阶段引导调度模型
2021-12-09李金亮吴尚阳
杨 莹, 李金亮, 吴尚阳
(黑龙江科技大学 电气与控制工程学院, 哈尔滨 150022)
0 引 言
近年来,在全球环境不断恶化的背景下,电动汽车作为可再生能源的载体,其发展得到了国内外的广泛关注[1-2]。电动汽车的快速发展也给城市交通网以及电网带来了压力。规模化电动汽车无序的充电行为会对电网造成巨大冲击。因此,如何为电动汽车充电建立一个合理的引导及调度方案,成为了目前研究的热点。
目前,国内外学者已经开展了诸多电动汽车有序充电及调度方面的研究。李秋硕等[3]基于充电负荷时空双尺度可调节特性及可预测性,提出了电动汽车一种有序充电方法。Clement等[4]以电动汽车能量损耗最小为目标,提出一种随机规划方法实现协调插电式混合动力汽车充电行为。黄晶等[5]利用Floyd最短路径算法,以电动汽车出行起讫点为基础,结合道路路网,构建了一种电动汽车充电引导方案。严弈遥等[6]给出一种将电动汽车、交通路网和配电网作为一个整体的电动汽车充电路径规划算法,为需要充电的电动汽车规划了合适的行驶路径。结合道路权重思想与实际路网结构,以电动汽车用户的综合成本最优和充电站负荷分配均衡,以及负荷波动最小为目标,笔者提出了一种电动汽车最优充电站引导及充电车辆调度方案。
1 车-路-网充电站模型
1.1 模型描述与假设
对电动汽车进行充电站引导时,从用户侧出发主要考虑行程中产生的各种成本:里程、时间、费用及损耗成本等。其中,里程成本包括从出发点行驶至充电站的里程及充电结束后从充电站出发行驶至终点的里程;时间成本包括从出发点到充电站的路程耗时、在站充电的时长和完成充电后行驶至终点的路程耗时;费用成本为在站充电产生的充电费用及服务费;车辆损耗包括能量损耗、车辆磨损和蓄电池寿命损耗等。从充电站角度,希望服务的车辆数与自身充电设施数成正相关[7],产生的充电负荷对电网的冲击最小等。
为简化模型复杂度,文中在不影响目标的前提下,假设如下:
(1)电动汽车产生充电需求均为快充需求。
(2)充电站均设置为快速充电站。根据 QC/T 841—2010 《电动汽车传导式充电接口》对充电设施标准分类,文中充电功率设置为30与50 kW两种。
(3)不考虑电动汽车对配电网侧的直接影响,充电站作为联系配电网的关键环节,将电动汽车对配电网造成的影响简化为对充电站影响。
(4)在一段行程中,车辆自身损耗较小且难以测量,不予考虑。
(5)由于未触发充电需求时,车辆不需要进行引导,因此,触发充电需求前的行程不参与模型计算。
经以上假设,将用户里程、时间和费用成本最小,以及均衡充电设施服务率和充电站负荷方差最小作为目标函数进行后续研究。
1.2 实际路网模型
路网是电动汽车行驶的基础,文中利用图论描述路网内道路节点和不同道路之间的连接关系。图包含节点和弧段两种元素,如图1所示,节点代表实际路网内的道路交叉口,节点间线段则表示各个节点之间的连接关系。
根据图论描述方法,由图1可知,路网模型为
(1)
式中:V——道路路口节点集合;
E——道路有向弧段集合,代表两节点间的连接关系或单双向通行属性;
vi——节点编号;
m——节点数量。
eij——节点i与j连接关系;
L——路段长度权重集合;
lij——路段eij的长度;
R——道路等级权值集合;
rij——路段eij的道路等级。
当路段eij为双向通行路段时,有
eij=eji=1,∀i,j∈V,i≠j。
当道路eij为单向,i→j通行路段时,有
eij=1,eji=inf, ∀i,j∈V,i≠j,
根据OSM道路分级标准,文中抽取实际路网的部分主干道路,将道路分为三个等级,不同等级道路其通行时间和速度等实际道路属性不同。由图1可见,红色为一级道路,蓝色为二级道路,黑色为三级道路。
基于电动汽车实际行驶工况,文中对三种不同等级的道路建立了分级道路下的电动汽车单位里程耗电模型[8]为
(2)

由式(1)建立的交通路网模型,能够充分反映路网规模、道路长度、道路等级及道路通行能力等信息。
1.3 电动汽车单体模型
单体电动汽车参数包括电池参数、电动汽车耗能和充电需求判断模型。电动汽车出行模型为
CE=(O,D,to,Cp,Co,SL),
(3)
式中:O——电动汽车本次行程的起点;
D——电动汽车本次行程的终点;
to——行程起始时间;
Cp——电动汽车电池容量;
Co——电动汽车初始电量;
SL——电动汽车触发充电需求时的荷电状态。
文中为每一辆电动汽车随机分配出行起点O与目的地D,以及行程起始时间to。
1.3.1 电池参数模型
通过对EV数据库中电池容量数据进行拟合,得到电动汽车电池容量模型,Cp满足伽马分布[9]为
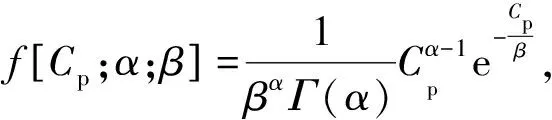
式中,α、β——伽马分布参数。
电动汽车在首次出行时,电量不一定为充满状态,因此,文中设置电动汽车初始电量为Co。设定初始荷电状态(SOC)服从N(0.8,0.1)正态分布[10],可得电动汽车的初始电量为
(4)
式中,σ、μ——正态分布参数。
1.3.2 电动汽车充电需求判断模型
电动汽车在途中的实时耗能情况,通过计算可得到车辆t时刻剩余电量为
(5)
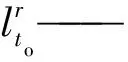
当前时刻电动汽车电量Ct小于阈值CL时,电动汽车触发充电需求,需要前往充电站进行电能补给。触发充电需求电量阈值为
CL=ω·Cp,
(6)
式中,ω——用户里程焦虑系数,服从区间0.15~0.30的均匀分布[11]。
1.3.3 电动汽车充电时长
电动汽车充电结束时的SOC值SF服从N(0.85,0.3)的正态分布[12]。由此可得,电动汽车充电时长为
(7)
式中:SS——电动汽车抵达充电站时的SOC值;
Pc——充电站充电功率;
η——充电效率。
(8)
式中:lr——电动汽车从触发充电时刻行驶至充电站所经过的r等级道路的长度。
1.3.4 充电负荷模型
充电站均设置为快速充电站,其中,每个充电站均视为10 kV配电网的一个集中负荷节点[13]。
t时刻在充电站k产生的电动汽车充电负荷计算式为
(9)
式中:ne(t)——t时刻正在充电的电动汽车数量,

2 最优充电站引导与调度模型
电动汽车用户在选择充电站时,会考虑多种因素。文中综合路段权值思想,将行驶里程、行程耗时和充电费用作为影响用户的主要因素,结合充电站充电设施服务率,提出了一种最优充电站引导策略。
2.1 一阶段充电站引导模型
文中目标函数主要从电动汽车用户在整个行程过程中的综合成本,以及充电站综合设施服务率两个方面进行考虑。用户综合成本包含里程、时间及费用成本。目标函数表达式为
(10)
式中:F1——用户行驶里程成本;
F2——行程耗时成本;
F3——费用成本;
F4——充电站充电设施服务率;
a1、a2、a3、a4——归一化权重系数,a1、a2、a3、a4之和为1。
2.1.1 电动汽车成本
电动汽车车主在选择目标充电站时,会将行驶里程作为首要的判断依据之一。电动汽车经充电站前往目的地所需行程里程为
(11)



时间成本也是用户主要考虑的目标之一,其时间成本表述为
(12)



充电费用作为充电产生的经济成本,也是用户在进行充电站选择时的关注点。充电费用为
(13)
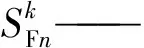
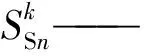
Mk——充电站k的充电电价, kW·h/元。
2.1.2 充电设施服务率
目前,由于国内充电站建设还处于基础阶段,加之在选择充电站时用户不会考虑对充电站造成的影响,经常以路程和行程耗时等作为选择充电站的依据,可能会产生车辆聚集于某一充电站的现象,导致排队时间过长,充电站容量不足, 造成“有站无车,有车无站”的现象。因此,文中引入充电设施服务率作为引导车辆的目标函数之一。
充电设施服务率表示为某一时间段内在站充电车辆数/充电站内充电设施个数。充电站k在t时刻的充电设施服务率为
(14)
式中,qk——充电站k的充电设施数。
2.2 二阶段电动汽车调度模型
对于前往充电站的电动汽车,文中将平抑充电产生的负荷波动作为目标,以负荷方差为目标函数对在站充电车辆进行充电调度,充电站k的负荷方差表达式为
(15)
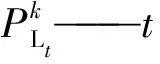
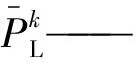
文中目标函数设置为
(16)
此调度模型为求解单目标函数,易于求解,文中采用粒子群算法对此调度模型进行求解。
2.3 约束条件
(1)电动汽车的剩余电量要足够支持电动汽车前往充电站,即
(2)电动汽车在选择充电站时,要对一些不合适的充电站进行排除,以此来减少工作量。设定里程约束为
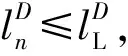

电动汽车前往充电站的行程里程不能超过其直接前往目的地的路程,且完成充电后,从充电站出发前往目的地的总行程里程,不大于其直接前往目的地的里程。
(3)每一辆电动汽车只能前往一个充电站进行充电,即有
最优充电引导及调度模型的系统流程如图2所示。站内调度方案如图3所示。
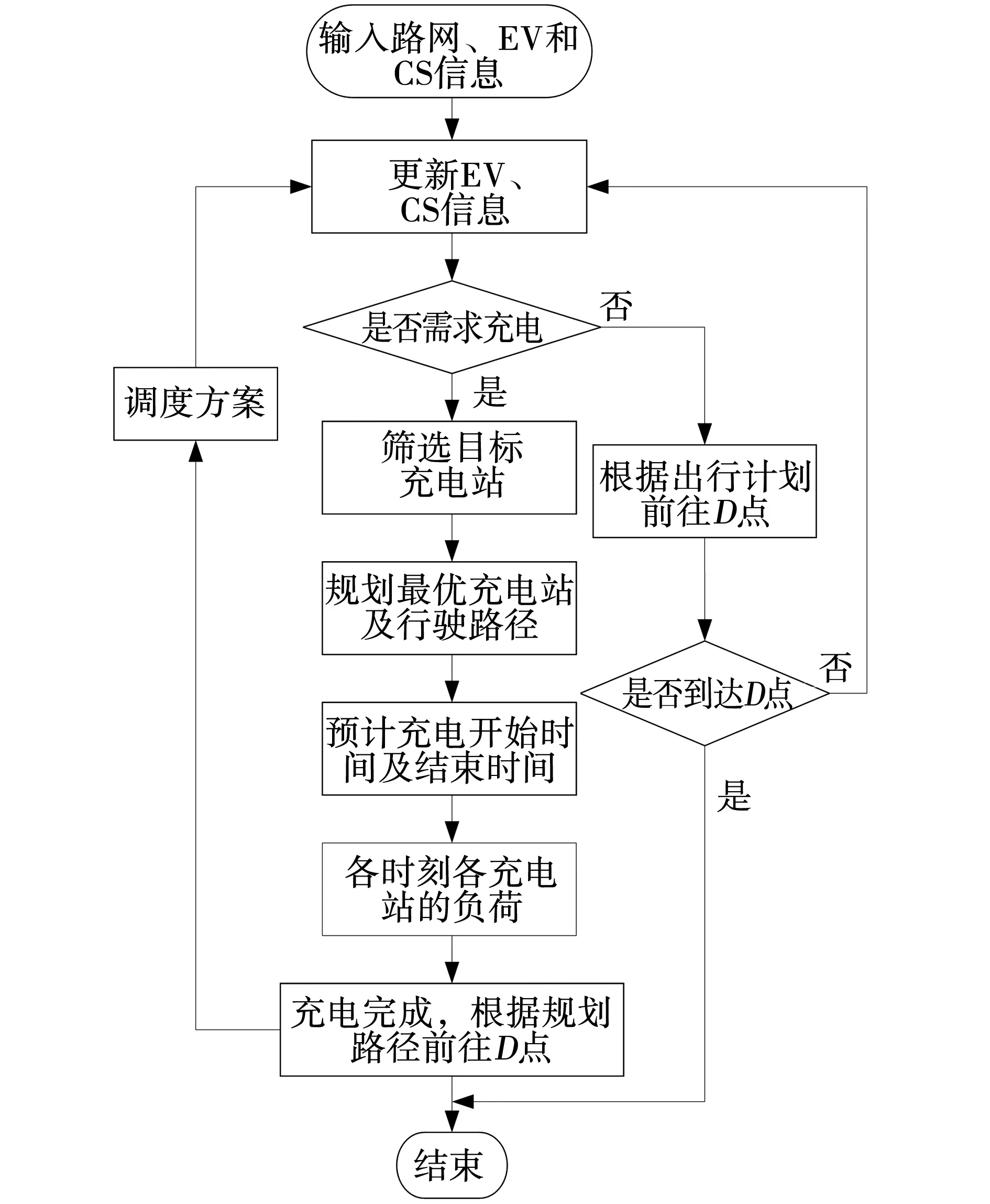
图2 最优充电引导及调度模型Fig. 2 Optimal charging guidance and scheduling model

图3 站内调度方案Fig. 3 Intra-station scheduling scheme
3 算例分析
3.1 仿真过程
以西安市某区域实际路网为例,如图4所示。结合该地区部分充电站,进行仿真分析。该区域内共有道路120条,道路节点72个,10个充电站分布于路网中,其中,一级路47条,二级路44条,三级路29条。
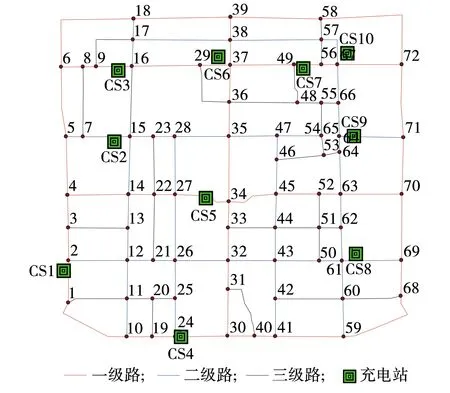
图4 路网拓扑及充电站位置示意Fig. 4 Schematic of road topology and charging station location
充电站信息如表1所示。其中,q为充电设施数。仿真时间选取早8时至晚20时,以15 min为间隔,共设置48个时间段,总时长12 h。在每个时间段内向路网投入100辆电动汽车,其初始位置与目的地位置随机分布于路网当中。电动汽车按照初始的路线从初始位置前往目的地位置,在电动汽车行驶过程中,实时监测其剩余电量,判断电动汽车是否触发充电需求,当剩余电量满足式(12)时,电动汽车触发充电需求,根据前文所述的方法为电动汽车推荐合适的充电站及规划前往充电站的路径。
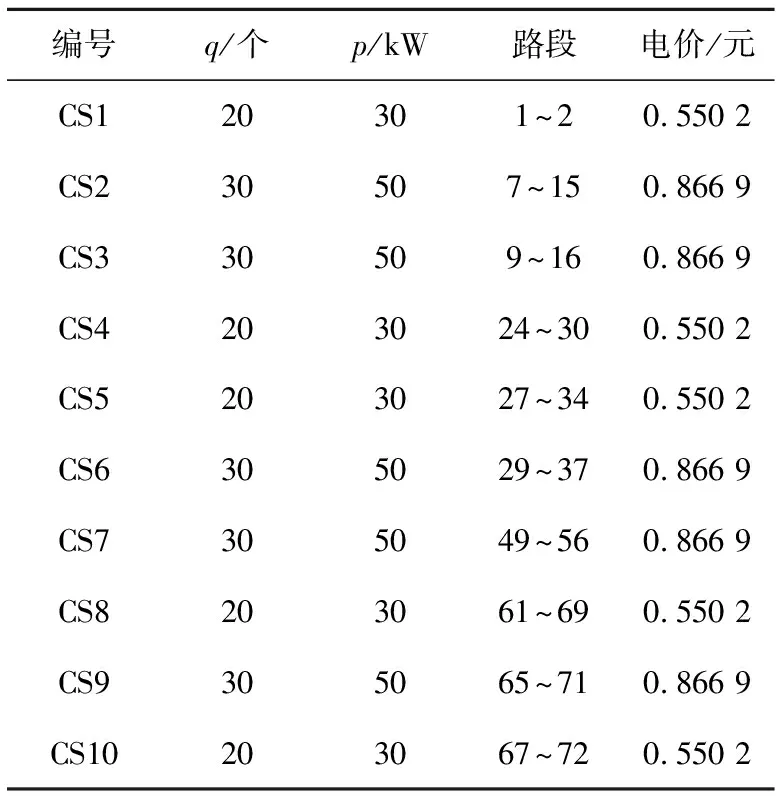
表1 充电站信息
3.2 结果分析
3.2.1 最优充电站的引导
以Dijkstra最短路径引导算法为例进行对比,各时段电动汽车引导结果对比如图5所示。
由图5可见,以仿真第一个小时的结果为例进行分析,当车辆采用Dijk最短路径算法引导时,在第三个时段内CS5需要服务的车辆多达63辆,设施服务率达到了210%,远超其充电设施数;同时,CS1、CS2只有1辆车抵达充电站,不能满足充电站对设施服务率的需求。充电站设施服务率分布于区间40%~440%,差异较大,导致设施资源浪费,以及各充电站负荷分配不均衡。
通过文中提出的引导方案对电动汽车充电过程进行引导,各时段内充电站服务车辆最多为15辆,各充电站充电设施服务率分布在113%~190%,能够满足充电站对充电设施的需求,大大提高了充电站的充电设施服务率,同时,各个时段充电站服务车辆数分配比较均匀,能够有效均衡充电站充电负荷。仿真第一个小时各充电站设施服务率如表2所示。其中,nDj为Dijk引导下的充电车辆数,nOp为文中所提引导方案下充电车辆数,sDj为Dijk引导下的设施服务率,sOp为文中所提引导方案下设施服务率。
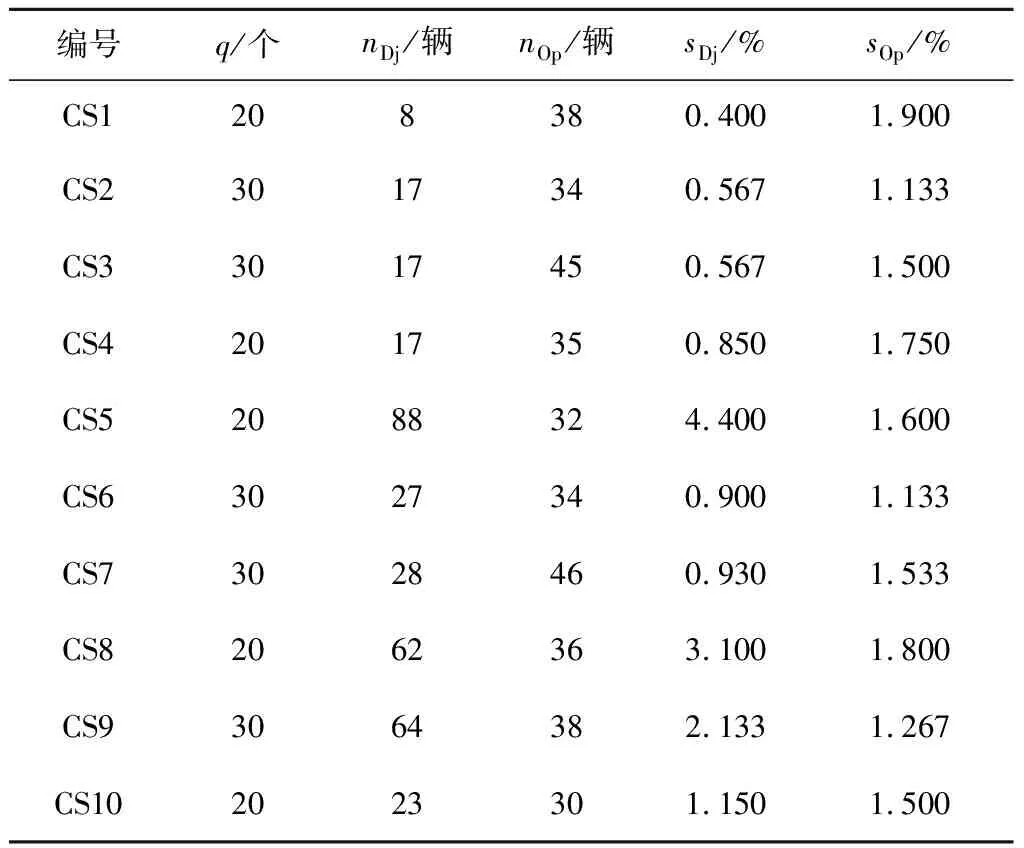
表2 前四个仿真时段充电设施服务率
对两种引导方法所产生的各项成本平均值进行对比,如表3所示。由表3可知,文中所推荐的充电站引导方法较Dijk最短路径算法相比,在里程成本有所增加,在路程耗时以及充电产生的费用上有所减少,但各项成本均无较大变化,在满足用户需求的同时,也能够保证充电站对设施服务率的需求。
最优充电站引导前后充电负荷如图6所示,Dijk引导下,充电站负荷均值分布于4.73×104~4.95×104之间,充电站间负荷差异较大,未能达到均衡充电站间负荷的目的。
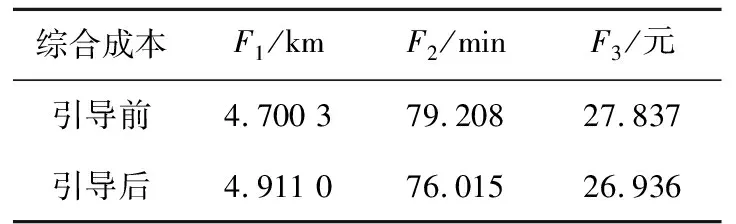
表3 综合成本对比

图6 引导前各充电站充电负荷Fig. 6 Charging load of charging station before guidance
通过文中方案引导后的各时段充电站负荷,如图7所示。各个时段有充电需求的电动汽车被较为均衡地分配到各个充电站,充电站平均负荷分布于4.80×104~4.84×104,且各时段充电站间负荷相差不大,提高充电设施服务率的同时,能够达到充电负荷均衡分配到每个充电站的目的。
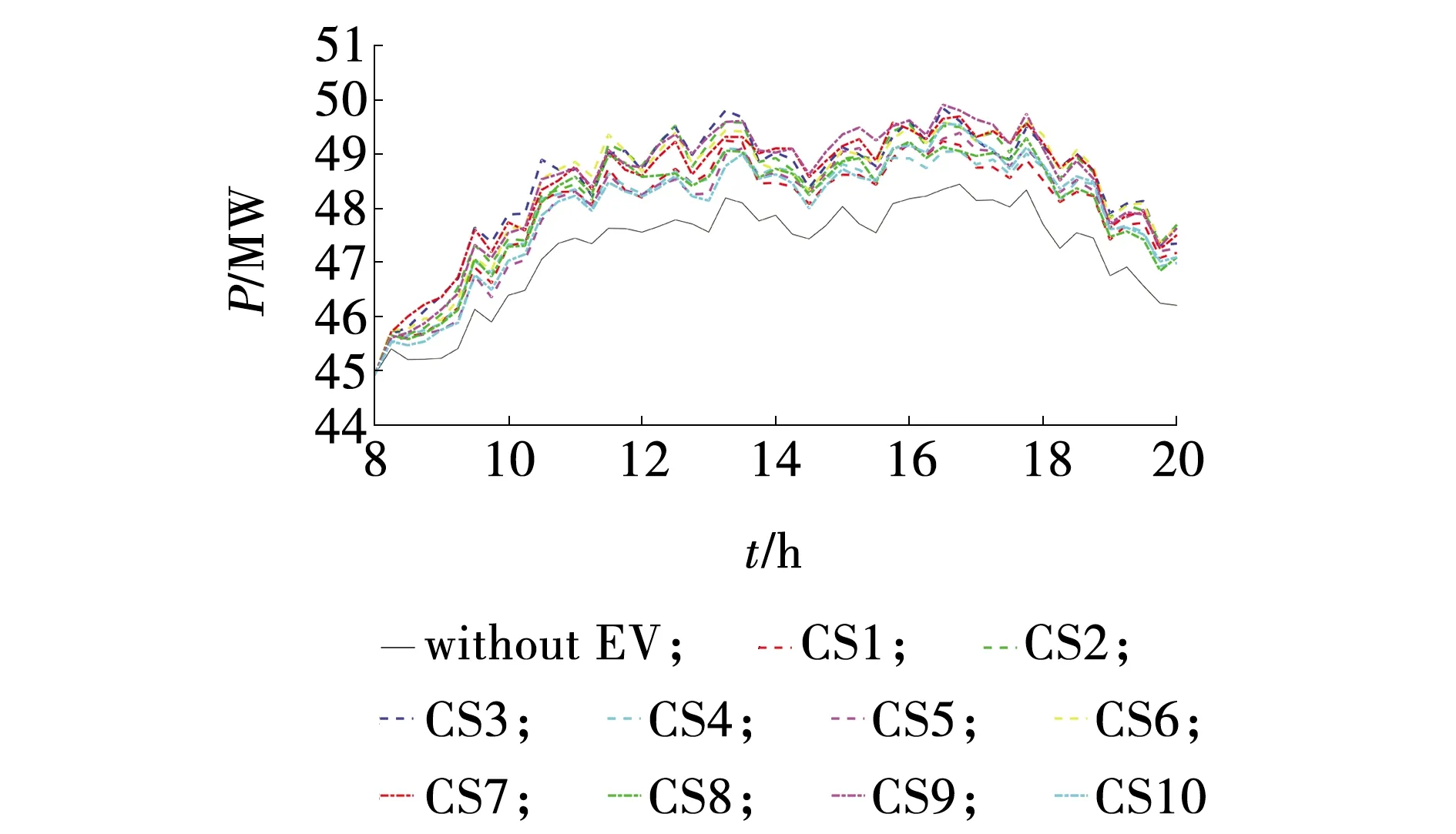
图7 引导后各充电站负荷Fig. 7 Charging load of charging station after guidance
3.2.2 电动汽车充电站的调度
经文中站内调度方案引导,各时段充电站产生充电负荷如图8所示,结果可以得出,经过对在站充电车辆充电行为进行合理调度,各时段充电站充电负荷波动情况明显下降,各充电站调度前后负荷方差如图9所示。

图8 调度后各充电站负荷Fig. 8 Load of each charging station after dispatching
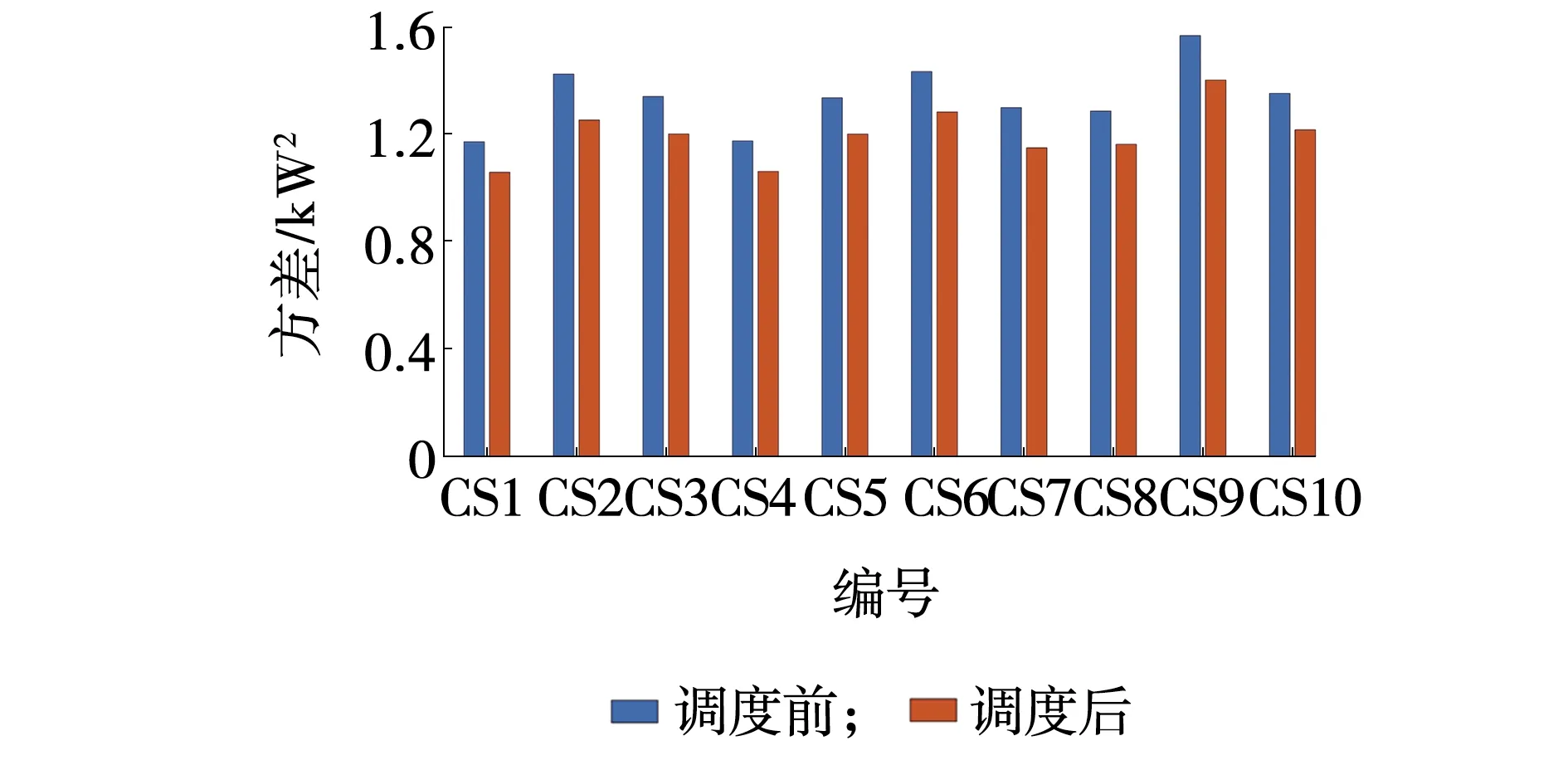
图9 调度前后各充电站负荷方差Fig. 9 Load variance of charging stations contrast
根据假设,以负荷方差代表电动汽车对配电网的影响,由图9可知,调度后的各充电站负荷方差较调度前下降了9.06%~13.01%,证明该调度模型能够有效减小负荷方差,平抑电网负荷波动。
4 结 论
(1)通过所提方案对有充电需求的电动汽车进行引导,能够有效平衡电动汽车用户的里程、时间及费用成本之间的综合需求,以及满足充电站对充电设施服务率要求,实现充电站服务车辆的均衡分配。
(2)通过引导充电车辆,能够有效缓解道路交通压力,合理规划电动汽车行驶路线,充电设施服务率达到了113%~190%,有效提高了充电设施服务率。
(3)以充电站负荷方差最小为目标,能够有效平抑充电站负荷,调度后的各充电站负荷方差较调度前下降了9.06%~13.01%,有效减少了电动汽车无序充电对电网造成的影响。
