交直流并行输电线路无线电干扰的预测算法

2021-12-08郑心仪唐波张嵩阳袁发庭刘钢李勃铖

南方电网技术 2021年10期

郑心仪，唐波,2，张嵩阳，袁发庭，刘钢，李勃铖

(1.三峡大学电气与新能源学院，湖北宜昌443002；2.湖北省输电线路工程技术研究中心，湖北宜昌443002；3.国网河南省电力公司电力科学研究院，郑州450002；4.国网湖南省电力有限公司输电检修分公司，湖南衡阳421000)

0 引言

随着我国经济和电力的发展，输电走廊资源日益紧缺，不可避免地出现越来越多的交流和直流输电线路并行在同一个走廊建设的情况[1]。而当交直流线路并行时，交流、直流电流相互耦合作用使得输电导线表面电场变化与电晕放电的规律相比传统单回输电线路差异较大，以至于难以准确预测其无线电干扰水平[2-3]。因此，亟需一种适用于工程应用且具有较高计算精度的无线电干扰预测算法，以帮助顺利开展交直流输电线路并行设计和电磁环境评价工作[4]。

实际上，国家标准分别给出了单独架设的交流输电线路和直流输电线路的无线电干扰水平预测算法[5]。工程实践上也根据相关标准分别采用激发函数法[6-9]和经验公式法[10]预测交流、直流线路的无线电干扰水平。然而，当交直流输电线路并行时，由于线路间存在电磁感应，相邻导线之间会因电容耦合和电感耦合产生干扰，不可避免地存在互耦效应[11]。这种耦合效应引起的离子漂移导致导线电晕现象与传统线路不同[12]。由此，文献[13]采用离子云模型对并行线路电晕放电的微观机理进行分析，认为直流线路表面电场叠加了交流分量呈现工频周期性变化，标准建议的单独交直流线路无线电干扰预测算法[5]不再适用。

为此，文献[14]最早认为交流和直流线路的电场相互独立，直接将总干扰水平视为求解两者平方和的平方根的结果。该方法虽然计算简单，但模型显然过于粗略。文献[2]利用线性叠加原理和BPA修正公式进行干扰水平求解，但计算精度仍然欠佳[15]。因此，国内外学者开始深入探讨交直流电场相互耦合的机理以提高计算精度。文献[16]提出了一种去离子场的分析方法，该方法虽然提高了计算精度，但忽略了交直流并行线路变化的电场对电晕产生离子轨迹的影响。文献[17]为分析直流线路的电晕损失问题，采用有限元和有限体积法计算了交直流输电线路产生的混合离子流场。文献[18]专门搭建了交直流并行线路电晕放电试验平台，以明确邻近直流电压时交流单点电晕放电下的电晕电流脉冲特性。在此基础上，文献[4]基于电磁干扰接收机准峰值响应模型，利用数值方法对交直流并行线路的无线电干扰数值进行预测。显然，这些数值模型的分析方法虽然一定程度解决了传统经验公式算法适用性不足的问题，但求解过程难免涉及到复杂的傅里叶变换或繁琐迭代过程，因此通常只能用于科学工作者的精确计算分析，难以被工程技术人员掌握。

同时还需要说明的是，上述这些预测模型仅针对导线本体电场进行研究，忽略了线路外界地理、气象、温湿度等复杂环境对其影响，而输电线路无线电干扰不仅与线路结构参数有关，还与地理环境因素关系密切[19]。如文献[20]通过对交流输电线路无线电干扰的长期测量，证明了干扰与环境气象参数间的相关性；文献[21]则发现交直流并行输电线路无线电干扰与湿度存在较强的负相关性。因此，考虑地理环境因素的影响，对无线电干扰的准确预测也至关重要。

因此，针对现有无线电干扰预测模型过于复杂而不利于工程人员掌握，以及干扰预测没有考虑外界工况影响的问题，本文考虑地理环境等多因素对无线电干扰的影响，以提高干扰预测的精度，同时在大量实测数据的基础上，采用BP神经网络实现对无线电干扰值与多影响因子之间复杂关系的数学拟合，从而为工程设计人员提出一种更容易掌握且准确的干扰预测方法。

1 交直流并行输电线路的无线电干扰

1.1 交直流并行输电线路的无线电干扰机理

交直流并行输电线路的无线电干扰是指交流线路与直流线路同走廊相距较近时，由于导线电晕电流向空间辐射的时变电磁场对外界无线电台站的干扰现象[9]。

当交直流输电线路并行架设时，交流线路的工频电磁场和直流线路的合成场之间相互耦合[3]。对于交流线路，直流线路会在原交流线路表面感应出固定的电荷，相当于在原线路表面场强的基础上叠加一个偏置场强。相应地，直流线路表面受交流线路调制感应出正弦变化的电荷，对应交流电压的正负半周，使得线路表面场强不再是恒定值。

因此，交直流输电线路并行时输电导线的表面场强处于不断变化中，再加上线路所经地区的环境因素对电磁场的影响，从而导致无线电干扰难以预测，给线路规划和设计工作带来了极大难度。

1.2 现有交直流并行输电线路无线电干扰求解方法

目前，对于交直流并行输电线路无线电干扰的求解，工程上技术人员还是倾向于计算便捷的需求[14]。计算过程可分为两步：首先采用经验公式法和激发函数法分别求得单独交流和直流线路的无线电干扰值；然后在此基础上经合成得到结果。即尽量保证合成后的干扰值与使用CISPR标准干扰测量仪器测量值相同的原则，当交流和直流线路无线电干扰之间相差大于3 dB时，取其中较大值为合成后的总无线电干扰；否则在二者平均值基础上叠加1.5 dB作为总无线电干扰值。或者，如同文献[14]直接认为交直流线路产生的无线电干扰是随机的，两者的相关系数为0，从而以交直流线路两者同频率无线电干扰水平平方和的平方根作为总干扰水平。

显然，上述合成算法虽然计算便捷易于被工程设计人员掌握，但实际上为了避免复杂求解，而对交直流线路之间电场的相互耦合影响进行了简化处理，由此求解出的干扰值与工程实际测量结果存在较大差异。

1.3 基于BP神经网络的求解思想

由于当前尚未有成熟且公认的交直流电场耦合作用表征用数学模型，倘若直接对交直流并行线路的无线电干扰预测进行精确建模，这对于普通工程设计人员来说过于艰难。因此，为便于工程设计人员掌握，必须避开交直流电场耦合作用的精确建模问题，这样需要另外寻求新的方法。

考虑到交直流并行线路的无线电干扰是受到地理环境和线路参数等多个影响因素共同作用的结果，因此干扰值的求解实际上是一个各影响因素为自变量，干扰值为因变量的一个非线性多元函数问题。再结合当前已存在投入运行的交直流并行输电线路，通过实测的方法获得大量无线电干扰样本，因此可以考虑利用这个有利条件，按照误差逆向传播的算法逐步训练对干扰值进行预测。因此，本文利用BP神经网络对非线性问题可进行高度拟合的优点，以此进行交直流并行输电线路无线电干扰值的预测。

然而，若将无线电干扰值的影响因素不经过筛选而直接作为自变量输入到神经网络中，网络输入层会因神经元数量过多而导致模型收敛速度慢，容易出现过拟合现象导致模型精度低[22-23]。因此，开始神经网络预测之前还需量化比较各影响因子对无线电干扰的重要程度，筛选出对无线电干扰值有切实影响的影响因素，从而极大程度避免神经网络收敛速度慢的问题。为解决这个问题，可考虑采用灰色关联分析算法来判断无线电干扰值与各影响因素之间的相关性，从而剔除对无线电干扰影响不大的指标。

2 交直流并行输电线路无线电干扰计算方法

2.1 无线电干扰的影响因素

由国标可知，针对交流和直流线路的无线电干扰主要由导线因素、线路结构因素以及地理环境因素三者共同影响[24]。上述3个因素对无线电干扰影响的具体表现形式如下。

1)线路表面场强是导线选择的基本条件[25]，而线路表面场强大小直接取决于导线运行电压。此外，导线直径、导线分裂数、导线截面也是传统线路表面场强计算表达式的重要组成部分[5]，在预测无线电干扰值时也应予以考虑。因此，导线因素包括导线运行电压、导线直径、导线分裂数和导线截面这4个影响因子。

2)线路结构和导线布置直接关系到无线电干扰特性[26]，其中导线架设间距通过影响临近导线的空间电荷分布改变无线电干扰的大小。根据文献[27]的研究结论，即导线高度对无线电干扰影响不大，同时考虑到试验场现场测点到导线投影距离时刻发生改变，最终选取测量点到导线距离这一与无线电干扰值呈直接负相关的影响因子[5]。另外，目前已投入运行的交直流并行输电线路中，交流架设形式普遍采用同杆并架双回结构，直流为双极线路[28]，故在此不考虑架设结构的影响。这样，最终需要考虑的线路结构因素具体包括导线架设间距和测量点到导线距离这2个影响因子[24]。

3)输电线路大多架设在野外露天环境，线路所处气压、温度、湿度和风速的改变使得线路表面场强发生变化[29]，以致对无线电干扰大小产生影响。因此，地理环境因素包括气压、温度、湿度和风速这4个影响因子。

当交直流输电线路并行建设时，上述导线因素和线路结构因素应单独区分交流和直流线路，而地理环境因素无需单独区分。依次以交流导线运行电压x1、直流导线运行电压x2、交流导线直径x3、直流导线直径x4、交流导线分裂数x5、直流导线分裂数x6、交流导线截面x7、直流导线截面x8、交流导线架设间距x9、直流导线架设间距x10、测量点到交流导线距离x11、测量点到直流导线距离x12、气压x13、温度x14、湿度x15和风速x16进行表示。此外，交直流线路并行间距x17的改变使得线路结构变化，从而影响无线电干扰大小[24]。综上，经上述分析可得无线电干扰的影响因子共分为11个，具体的影响指标达17个。

2.2 基于灰色关联度的指标筛选

利用灰色关联度理论对上述17个无线电干扰的影响指标进行精简，筛选其中的显著影响指标作为神经网络的输入变量。

设17个无线电干扰的影响指标子序列为{xi(j),i=1,2,…,17，j=1,2,…,n}，n为样本数目；无线电干扰值的母序列为{R(j)}。

数据分析之前，为避免因单位问题导致的数据大小问题，应首先对单位不一、初值不同的数据序列进行无量纲化处理，均值化公式为：

(1)

为得到无线电干扰各影响指标与无线电干扰值间的关联系数，从几何的角度，采用曲线间的差值大小作为关联度的衡量标准，可得无线电干扰值与影响指标间最小偏差值和最大偏差值为：

(2)

(3)

式中：Δi(j)为第j组数据中第i种影响指标与无线电干扰值的偏差值，Δi(j)=|R′(j)-xi′(j)|；Δmin、Δmax分别为各影响指标与无线电干扰值间的最小和最大偏差值。

每种影响指标与无线电干扰间的关联程度由n个关联系数共同反应，由于关联信息分散，从整体上比较较为困难，故使用求平均值的方法对关联系数作集中处理，则有

(4)

式中：γi为第i种影响指标与无线电干扰间的灰色关联度；γi(j)为第j组数据中第i种影响指标与无线电干扰的关联系数；ζ为分辨系数，用以避免最大偏差值过大而导致关联系数失真，ζ∈(0,1)。

鉴于上式，Δmin、Δmax、ζ在样本确立后均可看作定值，由此可见关联度γi与Δi(j)呈负相关，而Δi(j)具体表现为第i个影响指标的变化曲线与无线电干扰值曲线的差值或距离，若距离越大，则说明该影响指标对无线电干扰的影响不显著，可进行剔除；反之，说明该影响指标会对无线电干扰造成显著影响，即为对无线电干扰有切实影响的指标。

2.3 基于BP神经网络的无线电干扰预测

通过比较灰色关联度值的大小，假设筛选得到的显著影响指标数量为m，可得输入层输入神经元为{Yp(j),p=1,2,…,m}，输出层输出神经元为无线电干扰值{R(j)}。构建出的BP神经网络的基本结构如图1所示。

图1 无线电干扰的神经网络模型

由于实测数据的度量单位以及数值范围不同，为去除量纲、缩小数据范围以避免网络收敛速度慢的问题，采用归一化mapminmax函数得：

(5)

式中：Y′p(j)、R″(j)均为归一化后的数据，位于区间[0，1]；Yp max和Yp min分别为第p个影响指标在输入神经元序列Yp(j)中的最大值和最小值；Rmax和Rmin分别为无线电干扰值序列R(j)中的最大值和最小值。

神经网络的学习过程分为两个阶段。第一阶段信号正向传递，归一化后的无线电干扰影响指标数据通过输入层经隐含层处理，最终到达输出层输出获得无线电干扰的网络预测值。隐含层与输出层通过激活函数输出，为有效增强神经网络的非线性映射能力，选择具有很强可微性的sigmod函数为：

(6)

(7)

式中：ωpk为输入层第p个节点与隐含层第k个节点间的连接权值；bk为输入层与隐含层第k个节点间的偏置。

同理，可得输出层输出为：

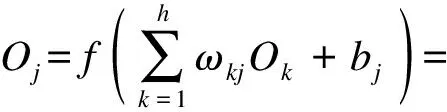
(8)

式中：Oj为第j组数据的无线电干扰网络预测值；ωkj为隐含层第k个节点与输出层间的连接权值；bj为隐含层与输出层间的偏置。

得到网络预测值后，学习过程的第二阶段通过比较网络预测值与无线电干扰值间的误差，不断调整层间连接参数的值，从而进一步缩小误差，使用的均方误差函数为：

(9)

式中：E为网络预测误差；R″(j)为第j组数据归一化后的无线电干扰值即网络的期望输出。

误差逆向传播通过梯度下降法逐步修正层间连接权值和偏置大小，使得网络预测值尽可能地接近期望输出，直至网络预测误差E<σ，其中σ为网络预设所需要达到的目标误差，即误差满足预设精度要求则结束算法，输出得到预测无线电干扰值。

2.4 交直流并行输电线路无线电干扰求解流程

结合上述“灰色关联度”和“BP神经网络”分析，首先利用灰色关联度理论筛选得到无线电干扰的显著影响指标，然后结合实测数据样本训练BP神经网络，直至误差精度满足要求，结束循环输出无线电干扰预测值。完整求解流程如图2所示。

图2 无线电干扰求解流程

3 交直流并行输电线路无线电干扰求解

3.1 数据整理和收集

为深入研究特高压交直流并行输电线路无线电干扰特征，以国标GB/T7349—2002《高压架空送电线、变电站无线电干扰测量方法》[30]为依据，在焦作±800 kV天中线与 500 kV博塔线并行段、湖州±800 kV锦苏线与1 000 kV湖安线并行段、上海±800 kV 复奉线与500 kV练亭、练卫并行段、四川±800 kV 锦苏线与500 kV二沐线并行段等多地已投入运行的交直流并行输电线路下方设立测量站，并在场地建立微气象站，对数据进行24 h的不间断监测及收集。

无线电干扰测量采用了德国SCHWARZBECK公司生产的FCKL1528测试仪，测试频率范围为 9 kHz～30 MHz；监测气象仪型号为NHFSX49，主要收集风向、风速、温度、湿度、气压等气象参数。测量站自2017年12月16日起开始运行，截至2018年3月25日共计收集了457 173条数据，建立了交直流电磁环境管理数据库。其中，焦作武陟段500 kV博塔线和±800 kV天中线并行线路的试验场现场监测示意图如图3所示。

图3 武陟试验场现场监测示意图

该交直流线路段并行间距76 m，交流500 kV博塔线采用4×LGJ-630/45型钢芯铝绞线，分裂间距500 mm，导线截面666 mm2，导线直径33.6 mm，导线间距21 m；直流±800 kV天中线采用六分裂JL/G2A-1 000/80导线，导线截面1 043 mm2，导线直径42.1 mm，极间距21 m。收集整理得到部分交直流并行线路无线电干扰以及气象数据样本如表1所示。

表1 交直流输电线路无线电干扰数据样本

3.2 关键影响因子的确立

根据灰色关联度相关计算原理，一般取分辨系数为区间的平均值ζ=0.5，此时较为容易观察出灰色关联度的变化。由此可建立灰色计算模型，通过计算可得到无线电干扰值与各相关影响指标间的灰色关联度如表2所示。

表2 无线电干扰各影响指标的灰色关联度

由表2可知各影响指标同无线电干扰值的灰色关联度大小，对其进行优势分析，其排序为x8>x7>x3>x4>x17>x2>x15>x13>x1>x9>x5>x10>x14>x12>x11>x6>x16，将灰色关联度值大于平均值0.768 2的9个影响指标视为显著影响指标，其中包含直流线路导线截面、交流线路导线截面、交流线路导线直径、直流线路导线直径、交直流线路并行间距、直流线路运行电压、湿度、气压和交流运行电压，其余影响指标的灰色关联度小于平均值，对无线电干扰值的影响相对较小，可将其舍弃。

3.3 BP神经网络训练

将筛选所得显著影响指标与无线电干扰值的数据样本进行归一化处理，输入MATLAB环境中进行神经网络训练。BP神经网络选用3层网络结构，输入层节点数与无线电干扰的显著影响指标数目相关，经灰色关联度分析共选取了9个显著影响指标，故输入层有9个节点；隐含层节点数的选取是确定网络结构的关键，而隐含层节点数大致为输入层节点数的2倍，通过综合考虑网络的训练效果、训练时间长度、模型的泛化能力等，最终选用的最优隐含层节点数为24；输出层只有1个节点，只输出无线电干扰值。确立神经网络的构造之后，在MATLAB中设置神经网络学习规则，设定最大训练次数为100 000，网络的学习速率为0.01，网络所要达到的目标误差为10-3。不断训练网络直至误差满足预设精度要求，训练停止。神经网络训练完成后进行验证，将反归一化处理后的BP神经网络拟合输出值同训练样本实际值进行误差分析对比，拟合曲线如图4所示。

图4 神经网络训练拟合曲线

由图4可知，BP神经网络模型拟合效果较好。通过对比BP神经网络拟合值曲线与训练样本实际值曲线间的差异，可得BP神经网络拟合值与训练样本实际值的绝对误差最大为1.26 dB(μV/m)，对应的相对误差最大值为3.14%。

3.4 预测结果及分析

运用上述训练完成的BP神经网络，随机选取表1中6组数据进行无线电干扰预测，将无线电干扰的显著影响指标数据经归一化处理后输入神经网络中，网络输出得到预测无线电干扰值。同时，利用传统的合成公式对该线路模型下的无线电干扰值进行计算，将合成法计算值和BP神经网络预测值同实测值进行对比，计算二者与实测值间的绝对误差，结果如表3所示。

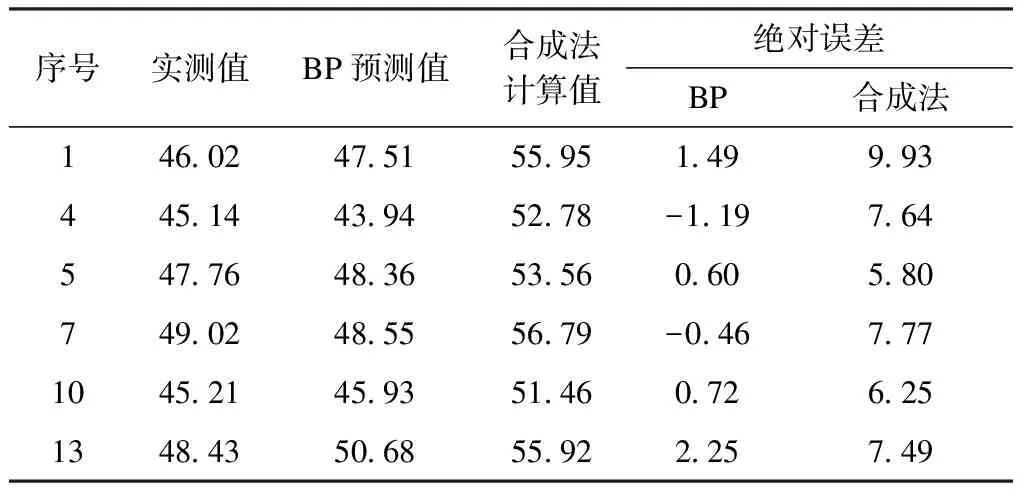
表3 无线电干扰预测结果

对表3中数据进行误差分析可知，传统合成法计算结果的平均相对误差为15.96%，而BP神经网络预测结果的平均相对误差为2.38%，其平均相对误差相较于合成法减小13.58%，由此可见BP神经网络预测法能获得更为准确的无线电干扰值。另外需要特别指出，BP神经网络预测结果精度依赖于测量样本质量，在利用BP神经网络预测前，需要获得准确的数据样本。