基于矩阵填充问题的五轮零知识身份认证方案

王后珍，蔡鑫伟，郭岩，张焕国

（1.武汉大学国家网络安全学院，湖北 武汉 430072；2.密码科学技术国家重点实验室，北京 100878）

1 引言

Goldwasser、Micali 等[1]给出了零知识身份认证的定义，其含义是P试图使V相信其掌握某个知识，或证明论断的正确性，但在该过程中V或第三方无法获得任何与知识相关的内容。整个交互过程的关键即如何做到使V无法获取与知识本身相关的任何信息。自从身份认证协议概念提出后，先后涌现了大批零知识身份认证协议，其中最具代表性协议包括FS 协议[2]、GQ 协议[3]以及Schnorr 协议[4]等。它们的安全性主要基于数论困难问题，如大整数因子分解问题（IFP,integer factorization problem）或有限域上的离散对数问题（DLP,discrete logarithm problem）。

Shor[5]在1994年设计了一种能够以多项式时间复杂度求解IFP和DLP的量子专用算法，也就是说，一旦造出可实用的量子计算机，基于上述数学困难问题设计的密码算法容易遭受攻击。现今密码学领域越来越重视抗量子计算密码的研究与探索，而且一些国家或组织正在积极开展抗量子计算密码算法的标准化工作[6]。

目前，已有的抗量子身份认证密码方案主要如下。1993 年美密会上，Stern[7]基于Syndrome Decoding 问题构造的认证密码方案。后来，文献[8-9]在Stern 方案的基础上做了进一步的优化，减小了Stern 方案的公钥尺寸，减少了交互过程中的数据传递量，并提升了协议的安全性。上述方案均是在有限域F2上设计的，而文献[10]则将上述方案拓展到有限域Fq上（q为素数）。2001 年亚密会上，Courtois[11]基于矩阵最小秩问题提出零知识认证协议；2011 年美密会上，Sakumoto 和Shirai 等[12]基于MQ 问题成功设计出安全实用的零知识认证协议。其他类似的方案有PKP 协议[13]、Chen 协议[14]、CLE 协议[15]、PPP 协议[16]、SC 协议[17]等。上述身份认证协议单轮的欺骗概率主要介于1/2～3/4，因此，工程应用中需要通过多轮迭代才能满足实际期望的安全性。2019 年，Yang 等[18]基于格上困难问题构造了一种欺骗概率可达到1/poly 的认证协议，不需要多轮迭代。2021 年，文献[19]借鉴Courtois方案的构造方法、基于矩阵填充（MC,matrix completion）问题构造了一种新型三轮零知识身份认证密码方案，相较于Courtois 方案，该方案在欺骗概率不变的情况下，减小了密钥尺寸，并提升了协议的运行效率。本文的主要工作如下。

1) 在文献[19]中认证协议的基础上，进一步将恶意证明者欺骗成功的概率由2/3 降至1/2，提出了基于低秩MC 问题的五轮零知识身份认证方案。

2) 针对新设计的五轮零知识身份认证协议，本文给出了其完备性、合理性以及零知识性的详细证明，证明了方案的安全性。

3) 最后给出了本文方案同其他现有方案的参数比较，指出本文方案所具备的优势。

2 预备知识

这里特别说明，本文的零知识身份认证密码协议均在有限域Fq上进行。其中，q=ph，h为正整数，p为素数。

2.1 零知识身份认证协议

在日常生活中经常会遇到这样的问题，一方P希望向另一方V证明他具备某种身份或知道某个知识，通常习惯称P为证明者，称V为验证者，这是基本的身份认证的问题。但为了进一步确保方案的安全性，人们希望该过程中V或第三方无法获得任何与知识相关的内容，也就是平时所说的零知识身份认证方案。

当方案分别满足以下3 个性质时，通常称该零知识身份认证方案是安全的。

完备性（completeness）。如果陈述为真，那么诚实的证明者在不违背交互协议的前提下，总能使诚实的验证者相信其确实拥有知识。

合理性（soundness）。如果陈述为假，那么恶意证明者几乎无法通过身份验证，诚实的验证者以绝对优势的概率返回拒绝，即恶意证明者成功通过验证的概率是可忽略的。下面给出正式定义。

定义1对任意概率多项式时间（PPT,probabilistic polynomial time）算法、验证者P以及输入x，存在提取器δ，如果有

其中，δs为欺骗概率，ε是不可忽略的，则提取器δ可在多项式时间内获得相应有效信息，且通过验证。

对于合理性这一性质有进一步的延伸，也就是特殊合理性，此处本文也对特殊合理性做简单说明。特殊合理性是指对于给定的公钥pk，当c1≠c2时，输出相同初始信息I的2 个可接收记录(I,c1,r1)和(I,c2,r2)是困难的。也就是说，对于任意的多项式时间敌手，其做出的响应只能通过挑战值中的一个。下面同样给出特殊合理性的定义。

定义2如果能够证明身份认证协议具备特殊合理性，那么对算法A而言，只要是PPT 算法，如下概率便可忽略不计。

其中，(pk,sk)由密钥算法生成，Rsp 表示对应记录验证者给出的判断。

零知识性（zero-knowledge）。当证明者真正拥有知识（私钥）信息时，诚实验证者或攻击者只要遵守协议运行规则，无论采用什么方法，如何对交互过程中的传输数据进行推导，均不能得到与知识本身相关的任何有效信息。下面给出对零知识性更规范定义。

定义3假如存在有效的模拟器U，对于验证者V和证明者P而言，以下二者是计算上不可区分的：

1) {P(sk),V(pk)}表示V和P在忠实执行交互后V所得到的知识信息，其中，sk 为私钥，pk 为公钥；

2) {U(pk)}表示输入为公钥pk、算法U的输出。则称该身份识别协议是诚实验证者零知识的。

另外需要指出，如果上述二者的分布是相同的，那么称该协议满足完美零知识性。如无特殊说明，本文后续的协议均指计算不可区分。为方便描述，上述完备性和合理性定义中的陈述均指证明者拥有知识这一断言。

2.2 相关NP 困难问题

下面分别简单描述矩阵最小秩（MR,min rank）问题和矩阵填充问题。

文献[20]较详细地描述了矩阵秩相关问题求解算法，矩阵最小秩问题就是其中之一，其求解思路是构造多变量非线性方程组，然后解方程组。另外，文献[21]也对MR 问题进行了详细分析。下面首先给出MR 问题的正式定义。

定义4（最小秩问题）设M0,M1,…,Mm为有限域Fq上的m×n矩阵，寻找一个向量使矩阵∑αiM i−M0的秩满足

与矩阵最小秩问题相似的另一个数学困难问题——矩阵填充是本文重点关注的。文献[22-24]给出了矩阵填充问题是NP 困难问题的证明，特别地，低秩矩阵填充问题的可表述如下

定义5（低秩矩阵填充问题）随机给定一个η×n维矩阵A=(aij)∈Fq且A的秩rank(A)=r，假如随机去掉矩阵中的m个元素。现对这m个空缺位置进行赋值，满足赋值后矩阵A'的秩仍然等于r。

矩阵填充问题属于NP 完全问题[18]。下节介绍该问题的求解方法。

2.3 MC 问题的常见求解算法

Harm 证明了MC 问题与MR 问题实际上是等价的[22]。这也就意味着最小秩问题的一些求解方法也可用于矩阵填充问题的求解[11]。假如随机选取秩为r的η×n维矩阵M∈Fq，参数ω为常量（2≤ω<3）。此外，定义缺失矩阵元素个数参数m，满足

那么目前低秩MC 问题常见的求解方法主要有以下几点。

1) 暴力破解。对缺失的元素进行穷举赋值，其时间复杂度为q mrω。

2) 子矩阵求解方法。Coppersmith 等[25]首先提出这种求解方法，文献[26]进一步对该类求解方法进行了论证，但只适用于r≪n的情形。实际意义不大。

3) Shamir 和Kipnis[27]提出了r≪n情形的另一种不同求解算法。其思想是将矩阵填充问题转化为一个多变量二次方程组。文献[28]对这种方法做了进一步改进，其时间复杂度为nO(r)。

4) 2000 年，Goubin 等[28]给出了一种称之为内核攻击的求解算法。当矩阵为方阵（n=η）时，该算法的时间复杂度约为。文献[29]做了进一步改进，给出了通用求解算法，其算法的时间复杂度为

5) 内核攻击方法是MC 问题的最有效的求解方法。2008 年，Faugere 等[30]对Kipnis 和Shamir的方法进行了优化改进，其时间复杂度为。需要说明的是，本文构造的零知识身份认证协议，其安全参数规模（包括有限域、矩阵维数及秩等）的选取依据将主要按照这种内核攻击求解算法。

3 基于MC 问题的五轮身份认证协议

本节给出五轮身份认证协议的具体构造。同之前的三轮方案[19]相比，增加了一次验证者和证明者之间的通信，增加的挑战值k∈(0,q)，因此，单轮攻击者欺骗概率降低至，显然，当q足够大时，欺骗概率约等于1/2。

3.1 协议构造

本文将该方案分为2 个阶段。首先是密钥生成阶段，其次是交互认证阶段。下面分别对这2 个阶段进行详述。

3.1.1 密钥生成

选定系统参数η,n,r,m和Fq。首先，随机选择一个η×n维矩阵A=(aij)∈Fq，且矩阵A满足秩rank(A)=r；然后，随机从矩阵A中去掉m个元素，将缺失m个元素的不完整矩阵记作A−，并用(i1,j1),…,(im,jm)分别表示这m个元素在矩阵A中的元素位置，ik代表矩阵行，jk代表矩阵列。

综上所述，该系统的公钥包含：η,n,r,m,Fq和A−，私钥为有序序列s，满足s={s1,…,sm}，其中，sk=aikjk,1≤k≤m。密钥生成过程即输入满足rank(A)=r的矩阵A，进行上述操作后，输出公私钥对(pk,sk)=((η,n,r,m,A−),s)。

3.1.2 单轮交互方案

证明者随机选择2 个可逆矩阵P和Q，其中矩阵P和Q分别为η×η、n×n维的方阵，并随机选取向量γ∈。证明者机将公钥不完整矩阵A−随机拆分为 2 个元素不完整矩阵之和，即满足等式A−=+，“+”代表相同位置元素相加，这里与三轮身份认证协议不同的是，本文指定元素有缺失的矩阵所有值位置均等于零，方便后续进行验证。这里需要说明的是这种拆法是公开的，据此拆分方法验证者同样可以得到残缺矩阵和。

证明者接下来秘密地将私钥s随机拆成α和β，满足分量β k=α k+sk,1≤k≤m；随后将α的m个元素逐次填充到缺失元素处得到矩阵A1，同理，将γ的m个元素也填充到得到矩阵A2。为了后续计算验证以及参数传递，证明者在本地分别计算M1和M2。其中，完整矩阵M1将由s的m个元素依次填充到得到，完整矩阵M2将由元素0依次填充到得到，之后计算矩阵M，矩阵M=PM1Q+PM2Q，显然矩阵M1和M2满足M1+M2=A。

五轮协议交互过程如图1 所示。

证明者和验证者共进行5 次交互，整个交互过程及每轮交互中的传递参数的详细描述如下。

1) 证明者先计算矩阵PA1Q和PA2Q，随后计算相应Hash 值，分别记作c1和c2，对应关系如下。

然后证明者将{c1,c2}发送给验证者。

2) 验证者从有限域Fq中随机选择一个值k，并将其发送给证明者。

3) 证明者计算矩阵N=PTQ并发送给验证者，这里矩阵T是通过将γ+kα+ks的元素逐次填充到得到的。

4) 验证者随机选择b∈{0,1}作为挑战值，并将b传至证明者。

5) 证明者根据b值向验证者做出不同的应答。

①如果b=0，则证明者将矩阵PA1Q、PM1Q、PM2Q和向量α发送至验证者，验证者收到后计算下述Hash 值

验证其与c1是否相等，并计算

然后验证相加后得到的矩阵PAQ的秩是否等于r。

② 如果b=1，证明者将向量β、矩阵P和矩阵Q发送给验证者，验证者首先验证P和Q是否为可逆矩阵，然后在本地计算下述Hash 值

逐次将β的元素填充到的空缺位置得到完整矩阵Y，验证c2和该Hash 值是否相等。

综上所述，同文献[19]设计的三轮交互协议相比，多出的一轮交互是验证者选择k值并将其传递给证明者；而证明者收到k后，利用该值计算一个矩阵N作为回应。k值也是能够将欺骗成功的概率降低到1/2 的关键。同时在参数生成时，五轮方案多了一个随机向量γ，该向量在验证者验证Hash值的时候起到了掩盖私钥的关键作用，从而确保在完成验证时并没有泄露私钥。

3.2 安全性证明

下面讨论本文身份认证方案的3 个重要性质，即完备性、合理性和零知识性。

3.2.1 完备性

定理1对于诚实的证明者而言，验证者可以检验证明者的身份。

证明在证明者和验证者都是诚实的以及不违背交互协议的前提下，证明者因为知道私钥s和在第二轮交互中验证者所选的k值，很明显可以在每一轮询问中计算出正确的c1和c2值，并返回给验证者相应的信息，进而证明其身份。即针对任何挑战值b，证明者做出的应答总能满足以下条件。

1) 当b=0时，有如下等式成立

2) 当b=1 时，有如下等式成立

3)P、Q均为可逆矩阵。

上述矩阵N=PTQ中的T可由γ+kα+ks的元素逐次填充至得到，矩阵1A和Y则分别为逐次将α和β的元素填充到矩阵元素空缺处后得到的完整矩阵。对任意轮次的询问，验证者都能正确检验证明者的身份。综上所述，验证者检验证明者的概率ε=1，因此，该协议满足完备性。证毕。

3.2.2 合理性

为了能够成功欺骗验证者，恶意证明者P′需要做以下准备，以应对验证者可能发起的挑战。同三轮方案不同的是，在传递过程中多了一个k值，如果P′猜到了正确的k值，那么便可以用k值来构造相应的c1和c2；如果P′未猜中对应的k值，那么P′仍然可以猜测b的值来尝试通过验证。将P′所做的准备记为{t1,t2}。在t1中，P′猜测收到的挑战值为b′=0，P′ 随机生成秩为r的矩阵A′，故rank(PA′Q)=rank(A′)，即矩阵PA′Q的秩为r，从而正确计算c1，而c2可以任意选取。综上所述，P′可以正确回答挑战b=0；在准备t2中，P′猜测收到的挑战值为b′=1，P′随机生成可逆矩阵P和Q，以及随机选择向量α*，而c1可以任意选取。由于恶意证明者并不拥有私钥，因此其无法对2 个挑战值均做出正确回应。因此，在每轮交互过程中{t1,t2}成功的概率为

这里假设验证者选取的k值不能为0，否则后续的验证便没有任何意义，所以上述等式中k′=k的概率为1/(q−1)。不过即使k值可以取0，当q达到一定阈值时，k k′=的概率仍然可以达到约1/2，其结果是相同的。通常需要将该身份认证协议重复w次，那么全部欺骗成功的概率为。如果恶意证明者P′可以响应验证者所有b值的挑战，则有如下定理。

定理2假如欺骗者能假冒证明者响应所有k值而且能被诚实验证者相信，则存在多项式时间概率图灵机能以不可忽略的概率，要么可以求解矩阵填充问题以恢复私钥，要么可以找到给定哈希函数的一个碰撞。

综上所述，证明者要么找到了一个给定Hash函数的碰撞，要么就有

即找到了矩阵填充问题的一个解。综上所述，该协议满足合理性。证毕。

3.2.3 零知识性

从图1 可以看出，在验证者和证明者的交互过程中，首先不会造成私钥s的泄露。当挑战b=0时，向量α是随机的，PM1Q和PM2Q均为随机矩阵，其相加后得到的PMQ为秩为r的随机矩阵，不能获得与矩阵M有关的任何信息，也就不能获得与私钥s有关的任何信息；当挑战b=1时，传输矩阵P和Q是随机选取的，向量β也是随机的，故并不会造成私钥s泄露。下面给出下述定理的证明，从而指出协议满足零知识性。

定理3在随机预言机模型下该身份认证协议（图1）为零知识交互认证协议。

如果想要证明这一点，需要构造模拟器U，满足其输出结果与协议诚实执行后输出是计算不可区分的。下面设计一个模拟器U来获取与真实文本计算不可区分的模拟文本，从而证明本文协议的零知识性。

证明假如模拟器U可以跟验证者进行通信。

1)U随机选取一个b′,b′∈{0,1}。

2)U随机选取可逆矩阵P、Q以及向量α和γ，U逐次将α和γ的元素填充到Ai−得到完整矩阵,这里i∈{1,2}，且分别计算PAiQ。若b′=0，随机选择秩为r的矩阵A′，将其拆分为M1+M2，M=PM1Q+PM2Q，计算c1=H(α,M,PA1Q,PA2Q)，任取c2即可；如果b′=1，则随机选择向量σ来代替私钥s，并计算c2=H(α+σ,P,Q,A2)，任取c1即可。

3)U随机选择一个非零值k∈Fq，并计算矩阵PTQ。若b=0，矩阵T可通过计算将PA2Q+kPM1Q得到，这里A2由将γ+kα的元素逐次填充到得到；如果b=1，矩阵T可通过将γ+kα+kσ的元素逐次填充到得到。

4) 模拟器U随机选择一个b∈{0,1}，若b≠b′，则直接返回步骤1)重新执行；若b=b′，则记录该轮交互过程。若b=b′=0，则U返回的信息{c1,c2,k,N,α,A′,PA1Q,PM1Q,PM2Q}是与真实值是计算不可区分的；若b=b′=1，则模拟器U返回的{c1,c2,k,N,P,Q,α+σ} 是与真实文本计算不可区分的。由于模拟器U可以同验证者进行任意次数的通信，因此模拟器可以重启整个认证协议直到猜对b值为止。

综上所述，该协议满足零知识性。

4 性能分析及方案比较

对于本文设计的五轮零知识身份认证方案，其安全性基于矩阵填充问题，所以根据2.3 节中的描述可知，当选取11×11 维的矩阵时，本文五轮身份认证协议具有80 bit 以上安全性，可以满足目前实际应用需求。因此本文身份认证方案在实际应用中推荐矩阵参数为有限域 F65521上的11 维方阵。

交互过程的前四轮较为简单，可以看出传递的参数为2 个Hash 值以及k值和b值（其中k∈Fq，b∈{0,1}），以及矩阵N，所以只需要传递(2×160 +lbq+ηnlbq+1)bit，其中q为有限域的特征数。同样，这里为了方便同其他方案做比较，故用于计算的Hash 值的长度为160 bit。

由上节中协议交互过程易知，当b=0时，传递的数据为向量α以及其他3 个维数为η×n的矩阵，向量α有m个元素，共计为(3ηnlbq+mlbq)bit；当b=1时，需传递矩阵P、Q以及向量β，共计(η2lbq+n2lbq+mlbq) bit，这里m为矩阵中缺失元素的个数。综上所述，整个交互过程所需要的比特数平均为

3.2.2 节中分析过，在q达到一定阈值时，单轮交互过程中的欺骗成功概率为1/2，所以如果想要达到10−6的安全性实际需求，通常至少需要交互20 轮以上。

表1 列举了80 bit 安全性水平下，本文方案与其他方案的比较结果，其中MC（五轮）代表本文所提方案。很显然，本文方案和MC（三轮）方案的公钥尺寸较小。通过比较可得，本文方案在公私钥以及参数尺寸并未发生变化的前提下，通过增加一轮交互，降低恶意证明者成功通过验证者身份认证的概率至1/2。同时单轮方案的通信开销虽然由于方案设计改变验证参数导致有所增加，但由于欺骗成功概率的降低，使达到相同安全性时交互轮次降低，故本文设计的五轮交互身份认证方案与MC（三轮）方案相比，总的通信开销相差不大，但进一步提高了协议的安全性。

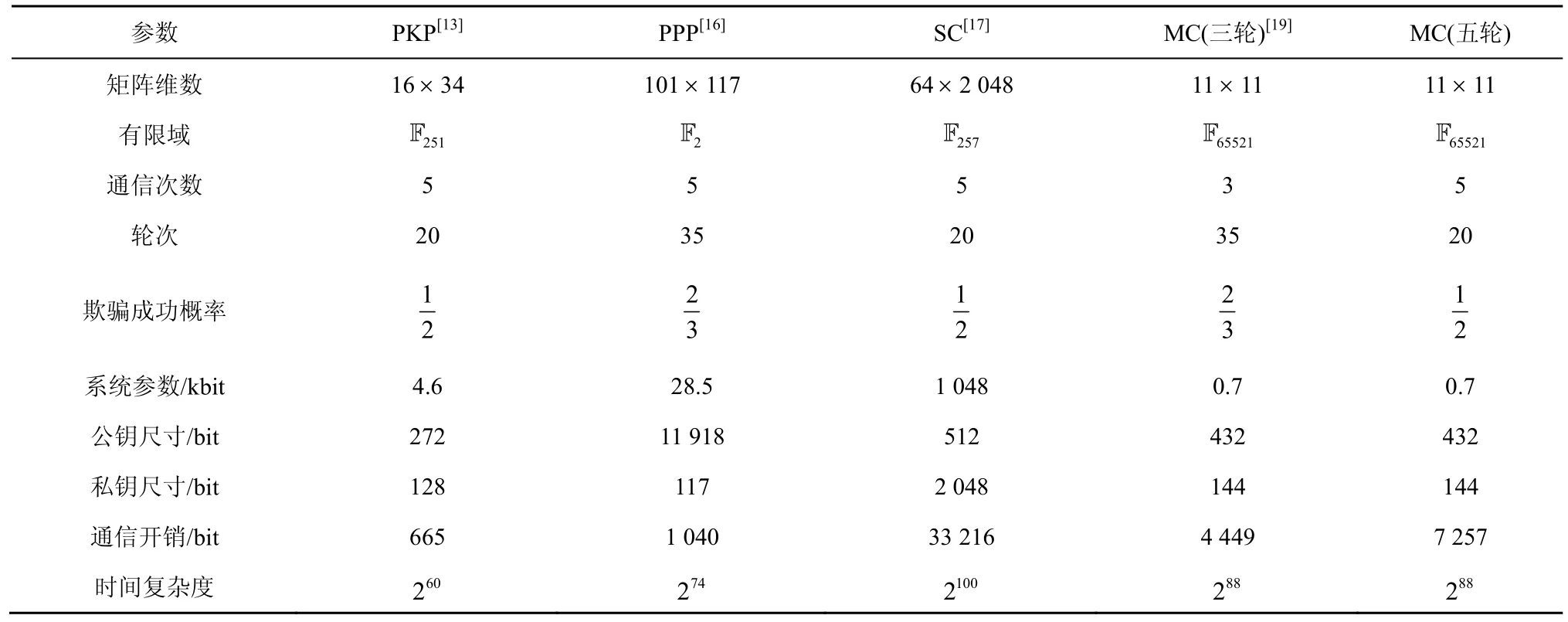
表1 参数比较

本文对几种典型的身份认证方案进行了实验比较，实验结果如表2 所示，本文方案实现效率比Stern 方案[7]和文献[19]方案要高，仅需4.6 ms。同时也不难发现，由于本文身份认证协议需要执行多轮，相较于基于数论困难问题设计的1 024 bit GQ 方案[3]和512 bit 的Schnorr 方案[4]，其实现效率略低一些，但在实际工程应用中仍然在可接受的范围，此外本文方案还具有抗量子计算攻击的优势。

表2 实现效率比较

5 结束语

本文基于（低秩）矩阵填充问题提出了一种五轮身份认证方案，相比已有的三轮方案，本文所提方案将单轮交互方案的欺骗成功概率从2/3 降低到1/2，并给出了欺骗概率的详细分析及严格安全性证明。以10−6安全性为例，五轮方案只需要重复执行20 次，而三轮方案需要执行35 次。所提身份认证方案具有很好的抗量子计算攻击潜力。而且基于本文提出身份认证方案，通过Fiat-Shamir密码转换技术，还可得到具有抗量子计算性质的数字签名方案[31-32]。

另外，能否在本文身份认证协议的基础上，优化参数降低通信开销，从而进一步提高协议的执行效率，值得进一步研究。