有效改造体积压裂效果评价方法及应用

2021-12-08马俊修兰正凯王丽荣易勇刚

特种油气藏 2021年5期

马俊修，兰正凯，王丽荣，易勇刚

(1.中国石油新疆油田分公司，新疆克拉玛依 834000；2.南京特雷西能源科技有限公司，北京 100020；3.中国地质大学(武汉)，湖北武汉 430074)

0 引言

非常规油气藏采用常规方法投产几乎无产能，需要采用水力压裂的手段来实现经济增产[1-6]。水力压裂形成的复杂缝网可有效提升油气在近井地带的渗流能力，从而大幅度提高非常规油气藏产能[7-8]。改造体积(SRV)最早由Mayerhofer等在研究页岩压裂时提出[9-10]，认为准确表征压裂缝网改造体积有助于多段压裂水平井的设计优化与压裂后生产效果预测。目前，SRV的评价方法主要包括数学模型法(解析法[11-12]和离散网络法[13-14])、倾斜仪测量法[15-16]、微地震反演法[17-18]等。离散网络法涉及大量的裂缝延伸模拟计算，存在计算资源要求高、计算耗时长的劣势，但能很好地刻画复杂缝网形态，与其他方法相比，是较为准确可靠的一种方法[13]。目前，基于离散网络法的SRV计算，只是将其等同于微地震侦测点的包络体[19]，而忽略了裂缝真实分布、生产动态响应等对SRV计算结果的影响。此外，学者对压裂水平井SRV的主控因素分析主要基于单一线性因素回归或多元线性回归等简单的数学处理方法[20-21]，而未考虑各控制因素间的相互影响。

因此，提出了一种基于非结构化网格的复杂缝网有效改造体积(ESRV)刻画方法，该方法考虑了实际生产过程中流体流动受基质和裂缝总压力分布的影响。利用该方法对新疆油田玛131井区水平多段压裂井进行了ESRV评价，以期为同类油藏水平井体积压裂优化与压裂后生产效果预测提供参考。

1 研究区概况

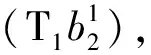
图1 准格尔盆地玛湖凹陷各区块位置分布

19.40 mD，平均为1.33 mD。

随着百口泉组砂砾岩油藏开发的逐渐深入，水平井增产效果明显，但存在以下问题：①水平井缝网精细刻画困难，常规方法无法刻画复杂裂缝的延展特征；②受到生产过程的影响，改造体积计算困难，且水平井的单井、井网参数对油藏开发的动用程度影响较大，需进行进一步评价；③影响改造体积的地质因素、工程因素较多，常规方法难以定量评价各因素的影响。

2 ESRV缝网精细刻画方法

前人在计算SRV时，主要以最边界的裂缝点为外边界，将该区域分割成许多同等大小的矩形，对矩形面积进行求和后，进一步乘以其地层深度，最终得到SRV[13]。由于实际流体流动受基质和裂缝总压力分布的影响，单纯由外边界构成的裂缝面积并不能完全描述实际生产对流体流动的影响，应根据生产过程中压力的分布来确定SRV，即有效改造体积(ESRV)。为使研究更具有代表性，选取生产过程达到拟稳态时的压力分布作为分析样本。当油藏定产生产达到拟稳态时，各压力的相对大小不变。因此，可根据此时的压力分布确定ESRV的边界及体积，步骤如下。

(1) 建立基于离散裂缝模拟方法的地质模型。基于离散裂缝网络的方法保留了精细网格加密的优势，生成网格简单、灵活，计算速度快、成本低，是目前复杂缝网刻画的有效数值模拟方法[21]。建立三维地质模型主要包括：①刻画分叉裂缝网络形态；②建立针对目标油气藏的裂缝启裂与扩展模型；③确定离散裂缝点坐标(主裂缝及诱导次裂缝的起裂位置网格)；④基于分叉裂缝网格模型构建离散模型；⑤输出离散模型的计算结果。该方法采用基于非结构化网格的离散裂缝数模技术，可以充分考虑实际储层的全三维非均质特征，精细表征压裂缝网几何形态(图2a)。

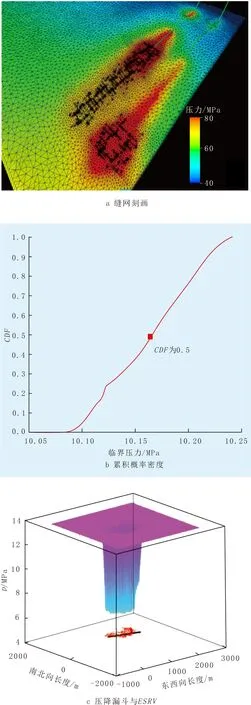
图2 基于非结构化网格的复杂缝网ESRV的刻画过程

(2) 确定拟稳态生产边界。由于拟稳态中各网格点的压力差保持不变，取井底和压裂范围内的某一网格，当2个网格的压力差随时间变化为定值时可认为达到拟稳态，按照式(1)确定该时刻非结构化网格中的压力分布。传导率会随着时间变化而变化(压力改变，黏度等参数也会改变)，但网格内流量的累计项也会随着时间改变，而压力场的相

对分布不变，因此，即使取拟稳态中不同时刻的传导率，求解的压力场不同，得到的ESRV边界也相同，即拟稳态中取不同时间的传导率对ESRV的确定没有影响。

(1)

式中：Δpi为网格i及相邻网格的压力差，MPa；T为传导率,m3/MPa；A为考虑压缩性的网格i的流量累计项,m3。

(3) 利用累积概率密度分布图计算ESRV。任取拟稳态中某一时刻的压力分布，绘制累积概率密度(CDF)与临界压力分布图。一般计算ESRV边界时CDF取值为0.9或0.5，而实际生产中取值为0.9过于乐观，由于非改造区域渗透率很低，实现生产时压力分布形成的漏斗区只位于场中的改造位置，边界区域的压力不变，导致不会出现全场达到拟稳态、压力统一下降的情况。因此，计算ESRV时CDF取0.5，找出压力比对应临界压力小的网格，将这些网格体积相加即可得到ESRV(图2b)。通过对压裂井进行快速衰竭开发数值模拟，得到呈漏斗型的全场压力分布，确定压力漏斗最剧烈的地方为改造区临界压力pe，进而确定改造区范围(图2c)。改造体积可由式(2)得到：

(2)

式中：pi为网格i的压力，MPa；pc为临界压力，MPa；Vi为网格i的体积，m3。

3 实例应用

以玛131井区MaHW1325井为例进行压裂缝网的ESRV刻画。MaHW1325井储层孔隙度为7.50%～14.30%，平均为9.58%，气测渗透率主要为0.03～17.20 mD，平均为0.96 mD。MaHW1325井共压裂了26级，平均每级压裂液用量为772 m3，支撑剂用量为70 m3。该井在1～17级进行了微地震监测，剔除无效点后，有效监测数据为1～12级。利用基于微地震监测数据的人工压裂缝网自动重构方法，通过压力传导关系确定压降漏斗的影响范围，最终确定该井的ESRV(图3)。

图3 玛HW1325井ESRV及各段ESRV精细刻画

基于压力漏斗，可以得到每口单井的ESRV，将单井ESRV网格体积进行累加，便可得到井区的ESRV。由于该油藏不同裂缝段压裂结果差异较大，为更好地研究水平井体积压裂效果与压裂参数的影响，分析体积压裂主控因素，根据每段裂缝的压力，可以进一步区分各段裂缝的ESRV，为压裂效果评估及数据分析提供了更加丰富的数据参考(图3c)。

将通过压降漏斗确定的ESRV与传统方式(微地震重构)估计的SRV结果进行对比，文中方法所获得的ESRV体积更小，平均相差16%，分析认为是传统方法中微地震监测到无效缝导致结果偏高(图4)。与传统方法相比，该方法减少了人工解释时主观因素带来的偏差，提高了ESRV的可靠性。

图4 玛HW1325井传统方法与ESRV方法解释结果对比

4 主控因素分析

在精确刻画ESRV的基础上，分析ESRV的主控因素，有助于提高分析结果的可靠性，为地质“甜点”优选、压裂施工参数优化等提供指导。

4.1 单因素ESRV控制因素分析

在按段统计ESRV的基础上，对ESRV与地质参数(孔隙度、渗透率、饱和度、单段油层钻遇长度、单段油层厚度等)、岩石力学参数(杨氏模量、泊松比、抗拉强度、孔隙压力、水平应力差、脆性指数)和压裂施工参数(单级压裂段长、压裂簇数、总液量、总加砂量、砂比、前置液比例、滑溜水比例、施工排量等)进行单因素的相关性分析。从单因素拟合结果来看(图5)，压裂缝网规模与单变量的相关性比较弱，缺少完整的正相关特征，认为压裂缝网规模应由多变量控制。

图5 压裂ESRV与地质、压裂施工参数相关性分析

4.2 多因素ESRV主控因素分析

线性算法、Lasso算法、项式(非线性)算法、二项式Lasso算法、随机森林算法是多因素分析中的常用算法，相关算法参考文献[22]。一般采用多数数据为训练组，少数数据为测试组来对比各算法的可靠性。为了优选出适合ESRV主控因素分析的算法，在单因素参数分析过程中，训练组使用75%的数据，测试组使用剩下的25%数据，开展多因素ESRV主控因素分析。结果表明，随机森林算法的计算ERSV与预测ESRV相关度最高，训练组相关性为0.88，测试组为0.45(图6)，其他算法的相关性小于0.70。因此，该文采用随机森林算法进行分析。

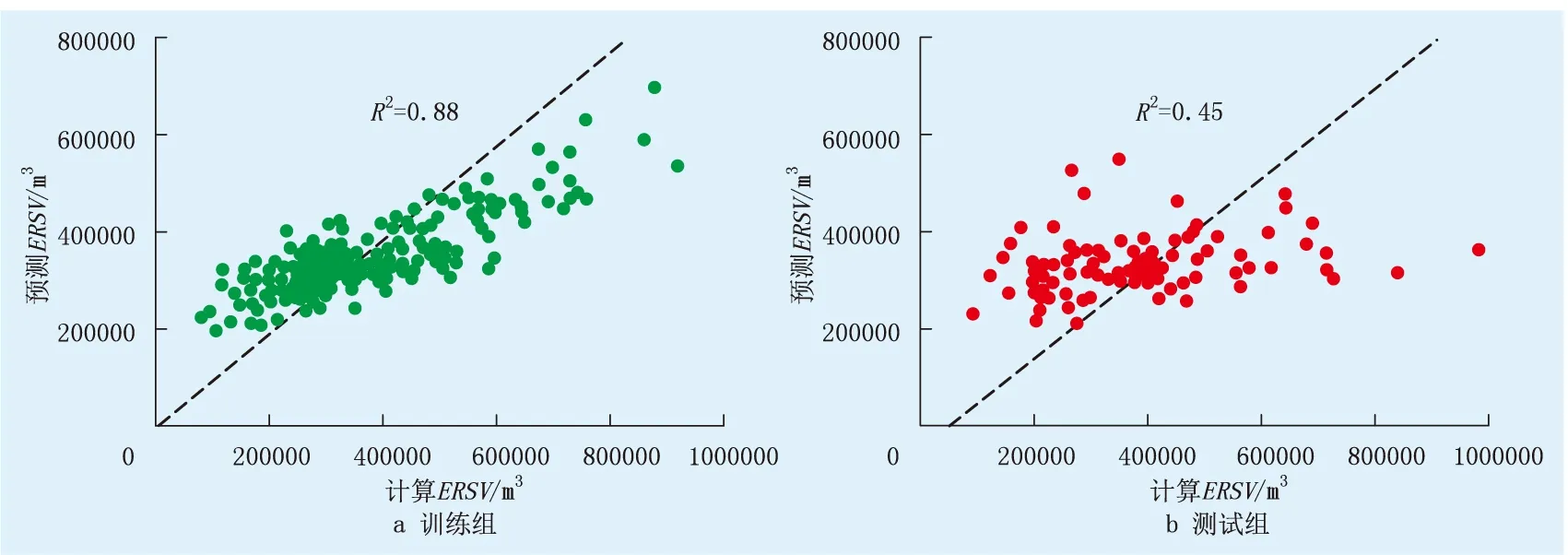
图6 随机森林算法计算结果

通过随机算法，开展影响ESRV的主控因素分级评价。由表1可知：一级主控因素中压裂施工参数的影响占53.8%，地质及岩石力学参数的影响占46.2%；二级主控因素在一级主控评价的基础上细分，压裂施工主控因素占比由大到小依次为单级压裂段长(12.08%)、总液量(8.47%)、砂比(7.39%)、滑溜水比例(6.85%)、总加砂量(6.36%)、施工排量(5.65%)、前置液比例(5.14%)、压裂簇数(1.86%)，地质及岩石力学参数主控因素占比由大到小依次为单段油层厚度(9.89%)、单段油层钻遇长度(4.99%)、抗拉强度(4.98%)、脆性指数(4.42%)、水平应力差(4.29%)、杨氏模量(4.05%)、含油饱和度(3.47%)、渗透率(3.31%)、孔隙度(1.48%)、泊松比(1.00%)。综合压裂施工数据、地质参数、岩石力学参数等分析结果可知，ESRV的结果受多因素共同影响。