经济型月球探测器精确定点软着陆制导算法

高 峰，荆武兴，高长生，李志刚，钟 伟

(1. 哈尔滨工业大学航天工程系，哈尔滨150001；2. 上海宇航系统工程研究所，上海201109)

0 引 言

作为21世纪航天领域的研究热点，深空探测吸引着越来越多的国家和科学技术人员进行深入的研究。而月球是人类开展外太空探测活动的第一颗地外天体，因此月球探测可以说是深空探测的开端。世界各航天大国对于月球探测的基本路线大体是“探”、“登”、“驻”[1]，所以建立月球基地、开发月球资源是实施月球探测计划的最终目标。针对这一目标，未来月球探测器的研发需要考虑两个方面的因素：一方面，需要运送大量的小型载荷到月球表面来建立月球通信网络，以提高未来月球探测器的自主能力[2]；另一方面，对月球资源的开采和运输需要探测器多次往返于地月之间。考虑到以上因素，若仍然采用传统月球探测器，探月成本必然十分高昂，因此经济型月球探测器将成为未来月球探测任务的不二之选，目前已知的相关项目包括NASA的“通用月球探测器”计划(Common lunar lander,CLL)[3]和“月球网络”计划(International lunar network,ILN)等[4]。与传统月球探测器不同，经济型月球探测器采用固体火箭发动机作为制动减速的主发动机，相较于液体火箭发动机，固体火箭发动机结构简单、加工和材料成本低廉，造价仅约为液体发动机的1/10～1/20，另外在主减速段结束之后，可以将其抛离，这样也很大程度上减少了随后过程的燃料消耗。但是采用固体发动机给制导律的设计带来较大的困难，液体发动机可以通过开关机和变推力技术实现对探测器运动状态的精确控制，而固体发动机不能做到随时开关机，只能燃料耗尽关机，同时也很难实现推力大小的精确改变。综上，需要对主发动机采用固体发动机的经济型月球探测器的制导律进行深入研究和设计。

软着陆任务对于制导算法有以下要求：燃耗最优或次优性、自主性、实时性、鲁棒性以及避障性能[5]。目前，月球软着陆制导方法主要有：月球垂线法、重力转弯法、标称轨迹法和显式制导法，而目前的研究重点主要集中在标称轨迹法和显式制导法。标称轨迹法包括标称轨迹优化和轨迹跟踪两部分，孙军伟等[6]通过将常推力月球软着陆轨道离散化，将原轨迹优化问题转化为非线性规划问题，并基于SQP(Squential quadratic programmin)方法对该问题进行了求解。彭祺擘等[7]将控制变量和终端时间作为优化变量，同时离散控制变量与状态变量，采用Gauss伪谱法对月球定点着陆最优轨迹进行快速优化设计。林晓辉等[8]在考虑敏感器视场约束及发动机推力大小约束的情况下，基于凸优化理论设计了月球软着陆的最优标称轨迹。对于轨迹跟踪算法的研究，Liu等[9]基于H∞理论设计了可以鲁棒追踪标称轨迹的最优反馈控制器。Wang等[10]提出了一种基于模糊神经网络的非线性最优控制策略。相较于标称轨迹法，显式制导法表现出良好的自主性和实时性，同时具备抗干扰能力，能够保证末端制导精度，具有一定的鲁棒性，但由于在求解过程中使用了必要的假设，所以显式制导算法的燃耗具有次优性。显式制导法是根据探测器的实时运动状态和终端状态，按控制泛函的显函数表达式进行实时解算的制导算法，该算法最早应用在日本SELENE-1探测器的设计方案中，随后众多学者对其进行了充分的研究。王大轶等[11]提出了一种燃料次优闭环制导方法，该方法以燃耗为最优性能指标，将制导指令表示为剩余时间的函数。王鹏基等[12]在显式制导方法中引入前馈控制，使得制导律能够消除初始偏差对末端状态的影响。孙军伟等[13]、Guo等[14]基于Pontryagin极大值原理设计了闭环多项式制导律。前期的显式制导律均没有考虑软着陆终端水平位置的约束，李茂登[15]通过忽略动力学方程中的高阶小量，采用变推力发动机，得到了能够满足末端全部位置约束的闭环显式制导律。另外在再入飞行器领域，Lu[16]提出了一种单基线预测校正再入制导算法，月球软着陆过程可借鉴该算法进行显式制导律设计。尽管目前的显式制导律具有自主性、实时性和易于工程实现的优点，但对于采用固体发动机作为主发动机进行减速制动的精确定点软着陆任务，由于传统显式制导算法在假设条件及制导指令解算方法上的局限性，并不能够满足全部的终端状态约束，因此有必要对其进行深入的研究。

基于上述分析，本文将对主发动机采用固体发动机的经济型月球探测器的在线闭环制导算法进行研究。首先在北东地坐标系下建立软着陆主减速段的质心动力学模型，然后依据动力学模型将探测器的运动分为纵向平面运动和横向运动，分别设计在线闭环制导律，最后通过数值仿真验证所设计算法的性能优劣。

1 月面着陆点全覆盖的环月调相策略

在月球探测任务中，探测器经双曲制动进入100×100 km环月轨道，然后经环月调相后最终机动到15×100 km环月轨道。在进行月面软着陆制动减速之前，探测器进行环月调相的主要目的是使探测器到达近月点时，预定的着陆点随月球自转刚好进入环月轨道面内，若此时开启主发动机进行主减速段制动，由于目标点已处于轨道面内，那么在探测器主减速段运动接近目标点的过程中，横向偏差(轨道面法向)将会很小，这样纵向平面(轨道面内)的运动通过固体主发动机产生的推力来控制，而横向运动由于偏差很小，只需采用横向小推力姿控发动机控制即可，从而为后续设计满足全部终端状态约束的在线闭环制导算法提供了基础。另外，为了满足未来建立月球通信网络和月球资源的开采、运输任务，需要探测器的着陆点能够覆盖月面包括极区在内的所有可着陆区域，因此选择月球极轨道作为环月轨道是一个很好的选择。通过环月调相等待，处于极轨道的探测器理论上可以软着陆到月面任意一点。基于上述考虑，下面进行精确环月调相策略的设计。

如图1所示，双曲制动结束后探测器进入环月轨道A点，设此时探测器位于A点的角距为ω1, 15×100 km环月轨道近月点C点的角距为ω2(由预定着陆点和软着陆过程的总航程决定)，根据几何约束关系：

当ω2≥ω1时：

(1)

当ω2<ω1时：

(2)

则探测器由A点运动到15×100 km环月轨道远月点B点所用的时间为：

(3)

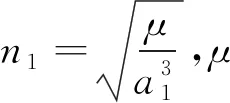
同理，探测器在15×100 km环月轨道由B点运动到C点所用的时间为：

(4)

式中：a2为15×100 km环月轨道半长轴。

设预定着陆点D点的月心经度为λ1，探测器位于A点时环月轨道升交点(或降交点)经度为λ2，定义：

Δλ=λ2-λ1

(5)

则预定着陆点随月球自转运动到轨道面内的总时间：

(6)

式中：ωm为月球自转角速度。

故可用于调相的时间为：

Δt=t-t1-t2

(7)

因此环月调相策略为：

Δt=ΣTi(i=1,2,3,…,)

(8)

式中：Ti(i=1,2,3,…,)为环月调相轨道周期。

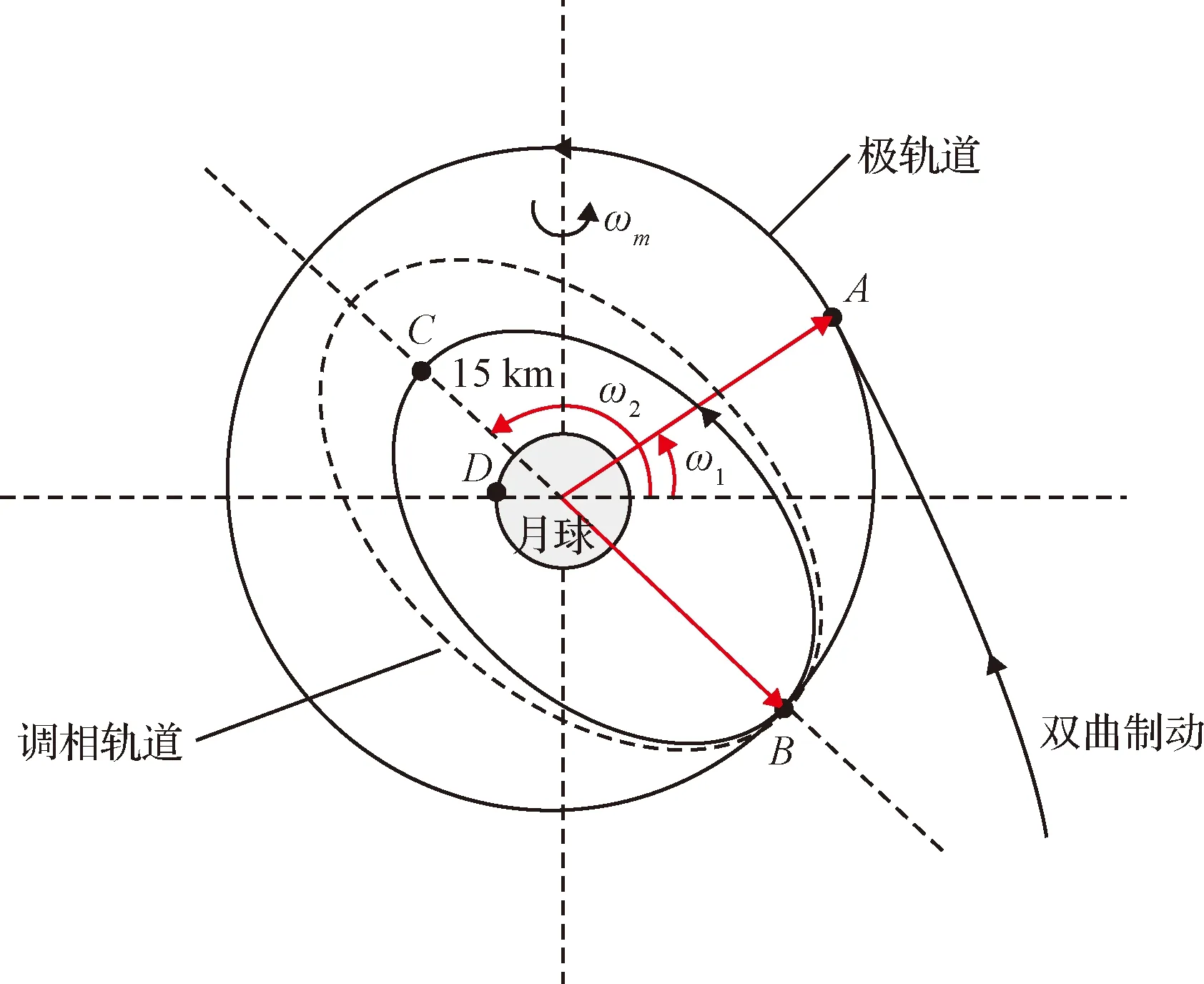
图1 环月调相策略示意图Fig.1 Strategy of phasing

按照上述环月调相策略，只需设计合适的环月调相轨道，即可使探测器在到达15 km近月点时，刚好预定着陆点随月球自转进入轨道面内，此时开启主发动机进行减速制动，同时启动横向小推力姿控发动机进行横向控制。

2 经济型月球探测器精确定点软着陆问题建模

通过第1节的分析，探测器位于15×100 km环月极轨道近月点时开始主减速段制动。为了方便对月球探测器软着陆制导方法进行研究，需要对动力学模型进行合理的简化。考虑到月球的自转角速度很小，而主减速段过程又很短，所以进行如下假设：1)忽略月球自转；2)忽略月球非球形引力摄动；3)忽略其他天体的引力摄动。根据牛顿第二定律，在图2所示的北东地坐标系下，探测器的质心动力学模型为：

(9)

式中：r=[0, 0, -r]T、v=[vx,vy,vz]T分别为探测器的位置和速度在北东地坐标系下的分量;φ为探测器所处的月心纬度;λ为探测器所处的月心经度;F=[Fx,Fy,Fz]T为发动机推力在北东地坐标系下的分量。

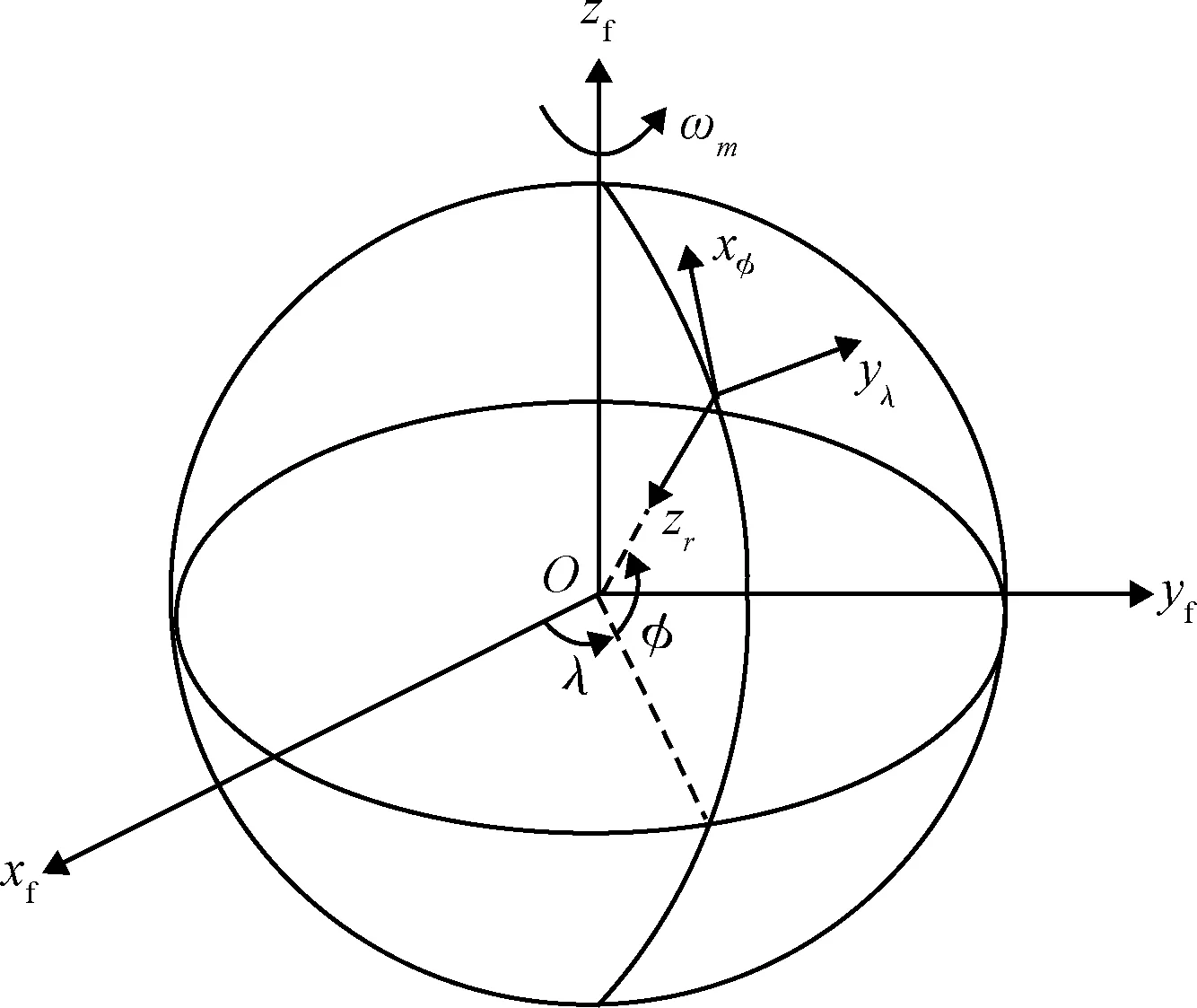
图2 软着陆主减速段坐标系Fig.2 Frames of main descent phase

考虑探测器质量的变化，其质量方程为：

(10)

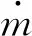
为了方便后续制导算法的设计，这里定义等效引力加速度：

(11)

由于r相对于vx、vy、vz要大得多，所以探测器在主减速段运动过程中，g′x、g′y、g′z近似为常值。

3 精确定点软着陆实时在线制导算法

对于配备固体发动机的经济型月球着陆器来说，在燃耗最优着陆的情况下，只控制推力方向而不改变推力大小，传统显式制导算法不能同时满足三个终端位置约束[11]。因此，根据式(9)以及第1节的分析，我们将探测器主减速段的运动分为纵向平面运动(x-z平面)和横向运动(y方向)两部分，然后分别设计在线闭环制导律。

如图3所示，在北东地坐标系下，纵向平面的运动通过固体主发动机产生的推力来控制，控制量为俯仰角αbn，同时在探测器运动过程中，保持偏航角βbn=90°或270°。对于横向运动控制，由第1节的分析可知，通过环月调相后，探测器在主减速段运动过程中横向偏差很小，若采用大推力固体发动机进行控制，很容易造成控制过量和偏航角在零值附近“振荡”的情况，所以横向采用小推力姿控发动机进行控制，控制量为发动机开关机指令u，u的值域为{-1, 0, +1}。在此控制策略下，推力在北东地坐标系下的分量为：

(12)

式中：F为固体发动机推力大小，Tr为姿控发动机推力大小。

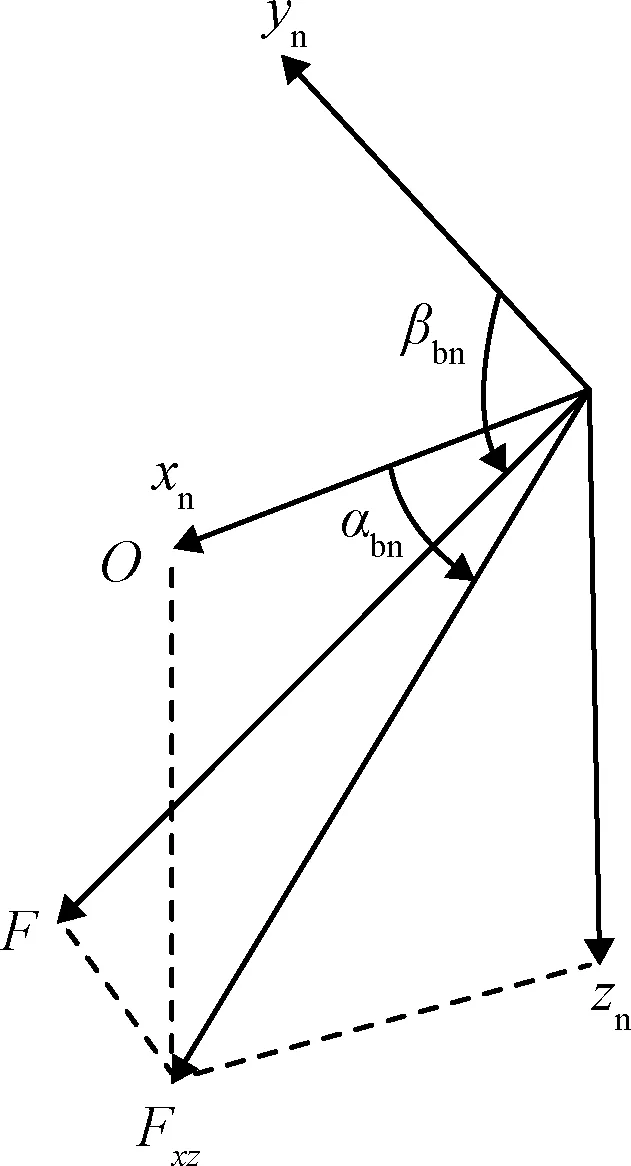
图3 固体发动机推力在北东地坐标系下的分量Fig.3 Thrust of solid rocket motor in the NED frame

3.1 纵向平面制导算法

3.1.1改进显式制导律

根据Pontryagin极大值原理，在固体发动机常值推力下，燃耗最优问题就等同于时间最优问题。令最优指标为：

(13)

引入Hamilton函数：

(14)

式中：λ=[λx,λvx,λz,λvz]T为纵向平面运动协态变量。

伴随方程为：

(15)

在不考虑位置约束的情况下：

λx=λz=0

(16)

λvx=λvx0,λvz=λvz0

(17)

由极值条件：

(18)

对式(9)进行对时间积分，可以得到：

(19)

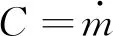
由上式可以得到不考虑位置约束下的俯仰角指令：

(20)

进一步，在考虑位置约束时，参考文献[11]的线性近似方法，设计纵向平面的显式制导律如下：

(21)

文献[11]将(l1+l2t)视为小量并对控制角的正弦和余弦进行一阶Taylor展开，然而在实际的仿真分析中发现(图4、图5)，在可达域内，除特定着陆点外，其余着陆点对应于位置约束的控制角常数项部分并不是小量，而只有一次项满足小量假设，同时上述处理方式会在主减速段末段局部时间内造成姿态角突变，从而增大姿控系统的工作难度。通过上述分析，下面对传统显式制导律作式(22)的改进，仅把一次项l2t作为小量，而常数项l1不作为小量，然后进行Taylor展开，可以看到改进的显式制导律满足上述假设，同时解决了末段姿态角突变的问题。

(22)

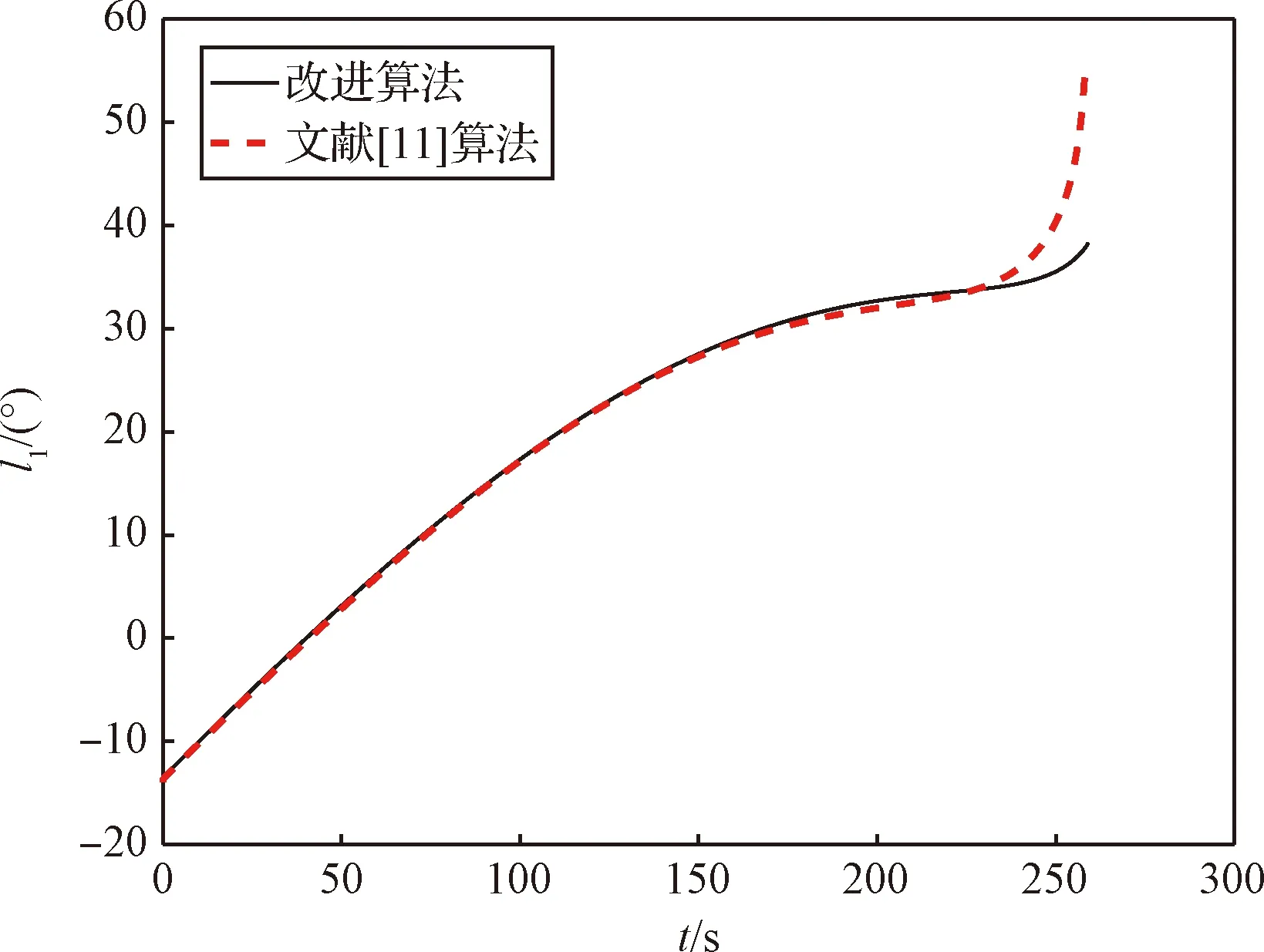
图4 l1变化曲线Fig.4 l1 curve

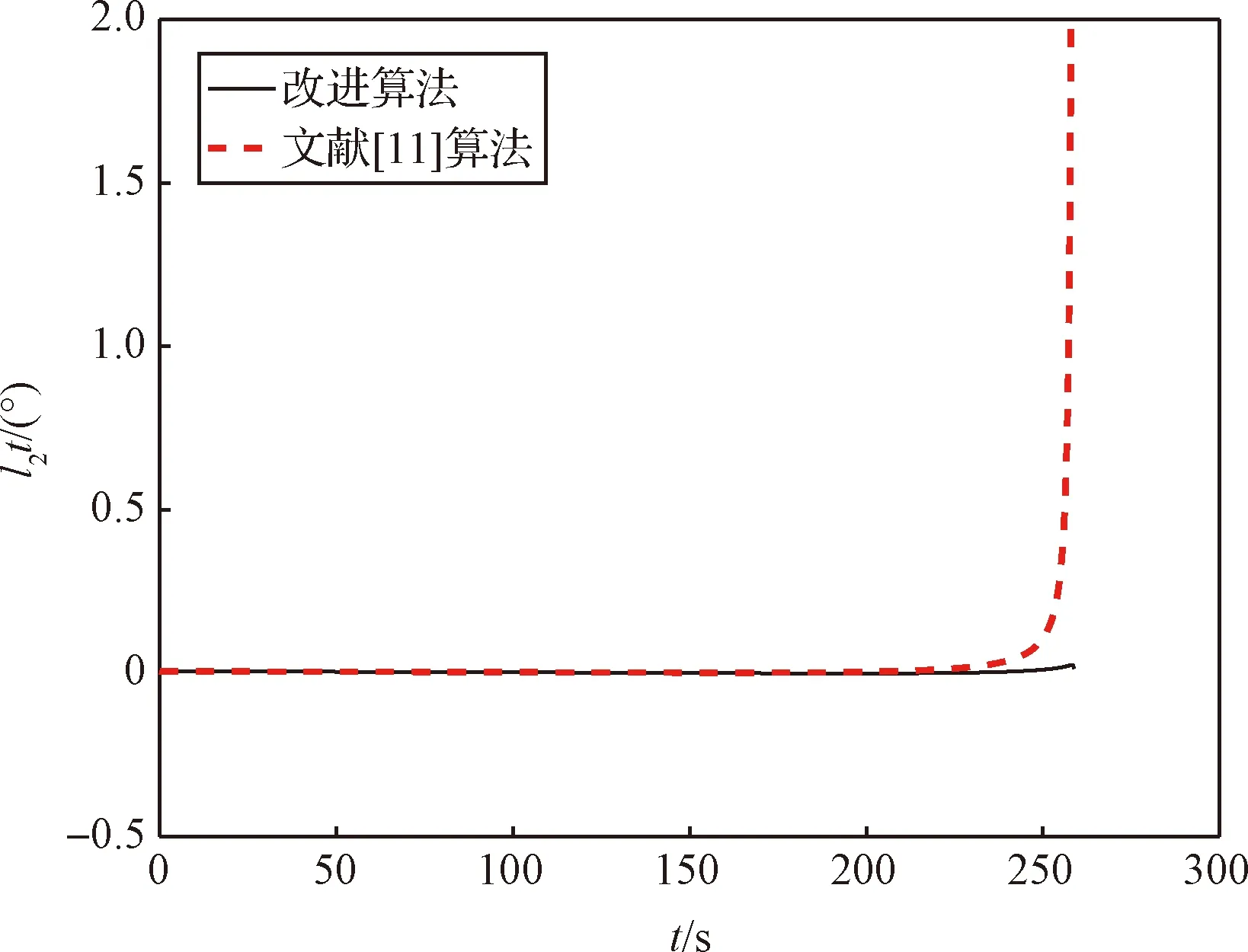
图5 l2变化曲线Fig.5 l2 curve

根据探测器径向zn的初始运动状态和终端状态约束，将式(22)代入式(9)并进行对时间一次积分和二次积分，可求得l1和l2的显式表达式。

3.1.2最优点火角搜索

在改进的显式制导算法中，控制角αbn的显式解与当前时刻探测器的径向位置坐标z0、终端径向位置坐标zf、纵向平面内探测器当前时刻的速度v0和终端速度vf以及剩余时间tgo有关，而与航向位置x0、xf无关，因此所设计制导律缺乏对航向位置的控制能力，为了实现精确定点软着陆，需要进一步设计探测器航向运动控制方法。

如图6所示，当探测器在15×100 km环月极轨道近月点开启点火制动时，若采用改进显式制导律飞行，除特定着陆点外，终端实际着陆点将超前(或滞后)理想预定着陆点。为解决这一问题，参考有限推力制导思想[17]，对点火点位置进行修正，以达到控制主减速段航程的目的。

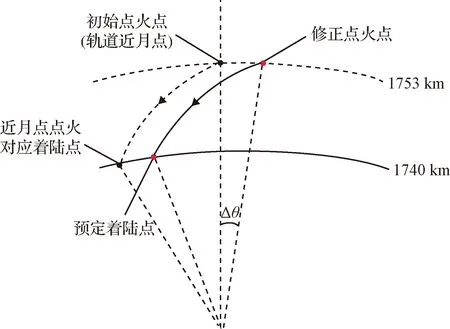
图6 主减速段点火点修正示意图Fig.6 Fire point correction of main descent phase

设点火点修正角为Δθ，通过仿真分析发现，在预定终端状态一定时，随着点火点位置的改变，主减速段采用改进显式制导律飞行的探测器航程变化不大。

图7 主减速段航程角随点火点位置变化Fig.7 Flight angle with fire point in main descent phase

另外主减速段末端状态误差变化如图8～图11所示，可以看到存在最优点火角Δθopt，使得探测器终端位置误差和速度误差达到最小。

图8 航向位置误差随点火点位置变化Fig.8 Course position error with fire point

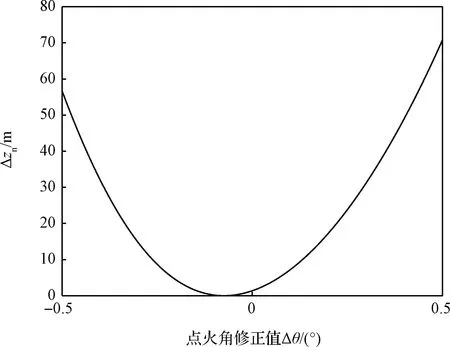
图9 径向位置误差随点火点位置变化Fig.9 Radial position error with fire point

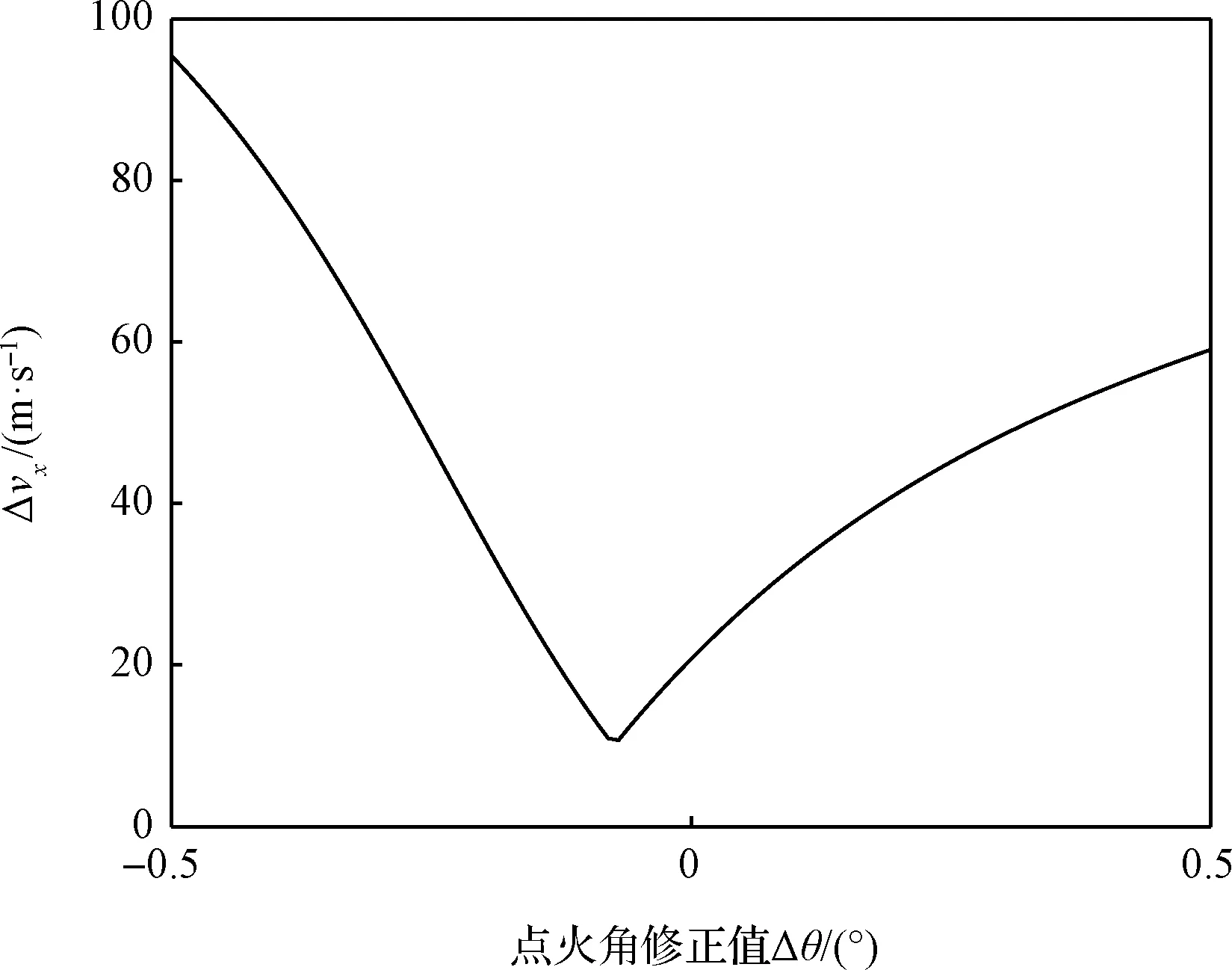
图10 航向速度误差随点火点位置变化Fig.10 Course velocity error with fire point

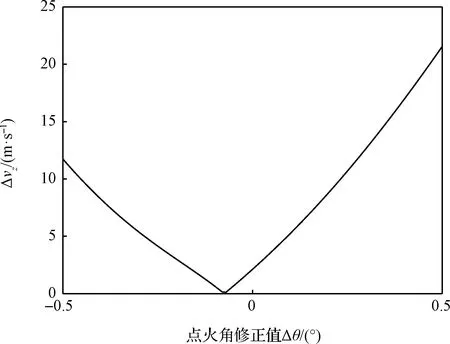
图11 径向速度误差随点火点位置变化Fig.11 Radial velocity error with fire point

通过上述分析，根据主减速段改进显式制导律的误差传播特性，设计如图12所示的点火点修正角搜索算法(Fire angle search algorithm, FASA)，δ为定点软着陆主减速段末端容许位置误差。在实际任务中，为了与后续阶段光滑过渡，一般要求在主减速段任务结束时，预定着陆点应位于探测器运动方向的前方，因此δ应大于0。另外，点火角搜索步长与环月轨道定轨精度有关，对于定轨精度位置偏差在300 m以内的月球探测器[18]，可设置点火角搜索步长为±0.01°(终端实际着陆点滞后理想预定着陆点时取+，终端实际着陆点超前理想预定着陆点时取-)。

图12 点火角搜索算法Fig.12 Fire Angle Search Algorithm

3.2 基于ZEM/ZEV方法的横向运动控制

软着陆主减速段横向运动控制采用ZEM/ZEV最优反馈制导律[19]，该方法具备燃耗最优、强鲁棒性和易于工程实现的特点。定义横向零控位置偏差yZEM和零控速度偏差vyZEV如下：

yZEM(t)=yf-y(tf)

(23)

vyZEV(t)=vyf-vy(tf)

(24)

式中：yf和vyf分别为预定着陆点的横向位置及横向速度，y(tf)和vy(tf)分别为在不施加控制情况下探测器在tf时刻的横向位置和横向速度。

对于式(9)和(12)，令ay=Tru/m，设计能量最优性能指标函数：

(25)

根据性能指标函数(25)得到Hamilton函数：

(26)

式中：λ=[λy,λvy]T为横向运动协态变量。

由极值条件以及伴随方程，可得最优控制量ay的表达式为：

ay=-λvy=-λy(tf)tgo-λvy(tf)

(27)

将式(27)代入式(9)并对时间积分，可以得到如下关系式：

(28)

(29)

式中：y0和vy0分别为探测器初始横向位置和横向速度。

由式(28)和(29)可得协态变量λy(tf)和λvy(tf)的解析表达式，将其代入式(27)可得ZEM/ZEV制导律为：

(30)

式(30)得到的制导律为连续控制变量，而横向运动控制采用小推力液体发动机来实现，控制量为发动机开关机指令u(u={-1, 0, +1})，因此需要将其转换为脉冲形式，下面基于PWPF对连续制导律进行调制[20]。

PWPF调制器工作原理如图13所示，其由一阶惯性环节、施密特触发器及反馈回路组成，km和tm分别为一阶惯性环节的增益和时间常数，Uon和Uoff分别为施密特触发器的开、关阀值，ay为横向运动连续制导指令，uy为调制脉冲输出。发动机最小工作时间为：

(31)

式中：h=Uon-Uoff为调制器迟滞，Um为脉冲幅值。

图13 PWPF调制器工作原理Fig.13 Structure of PWPF modulator

4 仿真算例

对于主发动机配备固体发动机的经济型月球探测器，由于固体发动机启动后必须持续工作到燃料耗尽，所以实际飞行中不能以运动状态作为发动机关机条件，而必须以质量变化量或推进时间作为终止条件。而在实际任务中，需要提前设计固体发动机的燃料装填量，因此仿真算例先以运动状态作为积分终止条件，然后根据主减速段全程飞行时间给出固发燃料装填质量参考值，最后以该参考值作为固体发动机终止条件来进一步验证所设计制导算法的性能优劣。

主减速段仿真参数见表1：

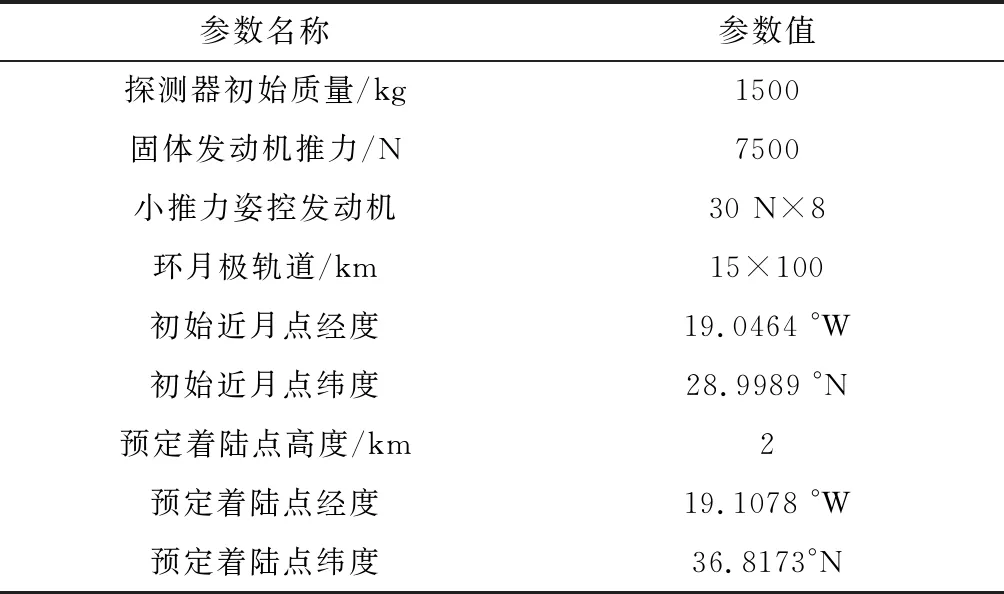
表1 主减速段仿真参数Table 1 Simulation parameters of main descent phase

4.1 FASA算法优化性能

首先根据FASA算法优化搜索点火角修正值。为了验证所设计点火角搜索算法的性能，在相同仿真条件下，选取终端航向位置误差为代价函数，分别采用粒子群优化算法(Particle swarm optimization,PSO)[21]、樽海鞘群优化算法(Salp swarm algorithm,SSA)[22]和本文所设计的点火角搜索算法(FASA)进行50次独立优化搜索，表2给出了三种算法代价函数值及平均搜索时间统计数据对比。

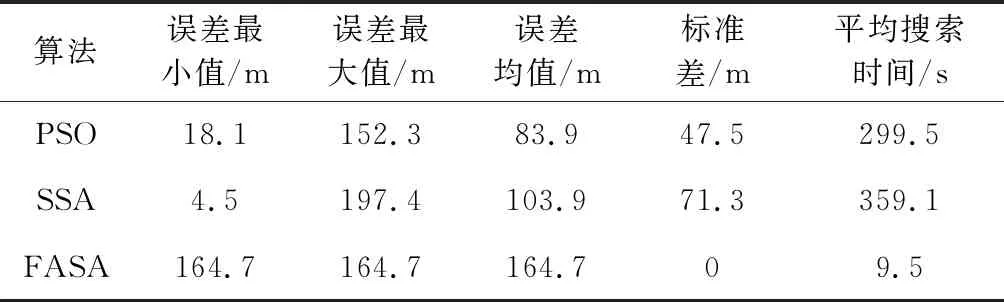
表2 点火角搜索结果统计Table 2 Fire angle search results statistics

由统计结果可以看出，三种算法的搜索结果都能够满足终端航向位置约束(容许位置误差200 m)的要求，虽然FASA算法的误差均值相比于PSO、SSA较大，但由于该算法的修正点火角初值是根据主减速段的误差传播特性得到，大大降低了初值猜测过程的随机性和迭代搜索次数，同时搜索过程采用固定步长，因此相较于其它两种算法多次搜索结果保持稳定。另外，FASA算法的搜索时间远小于其他两种算法，保证了在环月调相轨道周期内能够快速完成多次优化搜索，即使在探测器环月飞行过程中临时调整终端着陆点位置，也能够实时搜索到满足任务需求的点火角修正值，满足制导算法实时性的要求。

4.2 主减速段全程仿真

下面采用所设计的制导算法，以运动状态作为积分终止条件，进行主减速段全过程仿真，仿真中制导参数设置如下。纵向平面运动制导参数：制导周期T=0.08 s；点火角搜索结果：Δθcor=-0.08°。横向运动制导参数：km=6，tm=0.48，Uon=3.6×10-5，Uoff=3×10-6。仿真结果见图14～图19。

图14 径向位移曲线Fig.14 Radial position curve

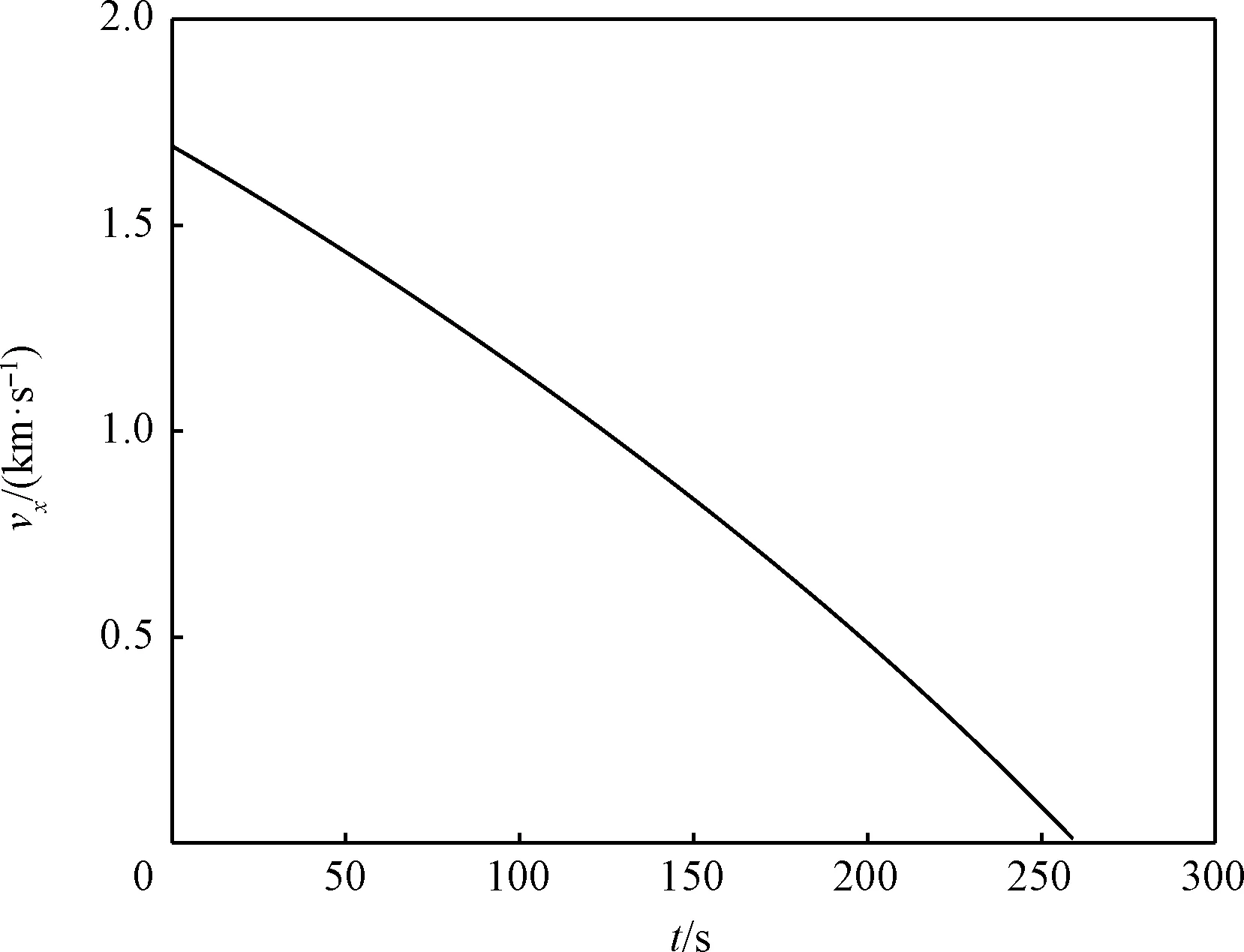
图15 航向速度曲线Fig.15 Course velocity curve

图16 横向速度曲线Fig.16 Lateral velocity curve

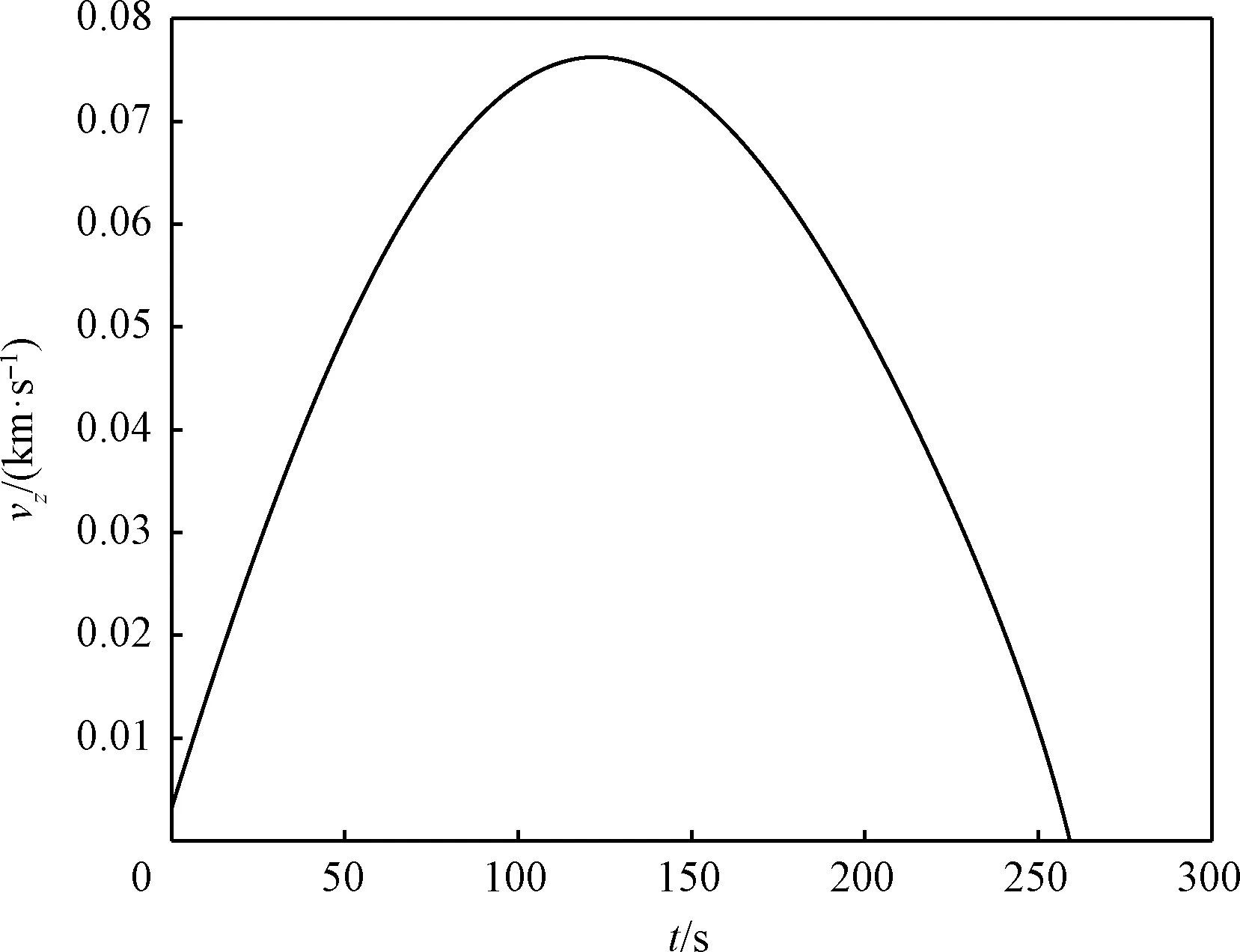
图17 径向速度曲线Fig.17 Radial velocity curve

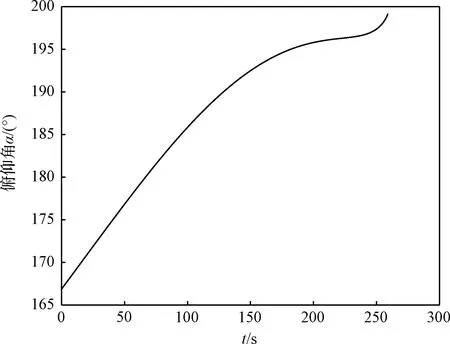
图18 纵向平面运动控制俯仰角指令Fig.18 Thrust pitch angle in longitudinal plane motion

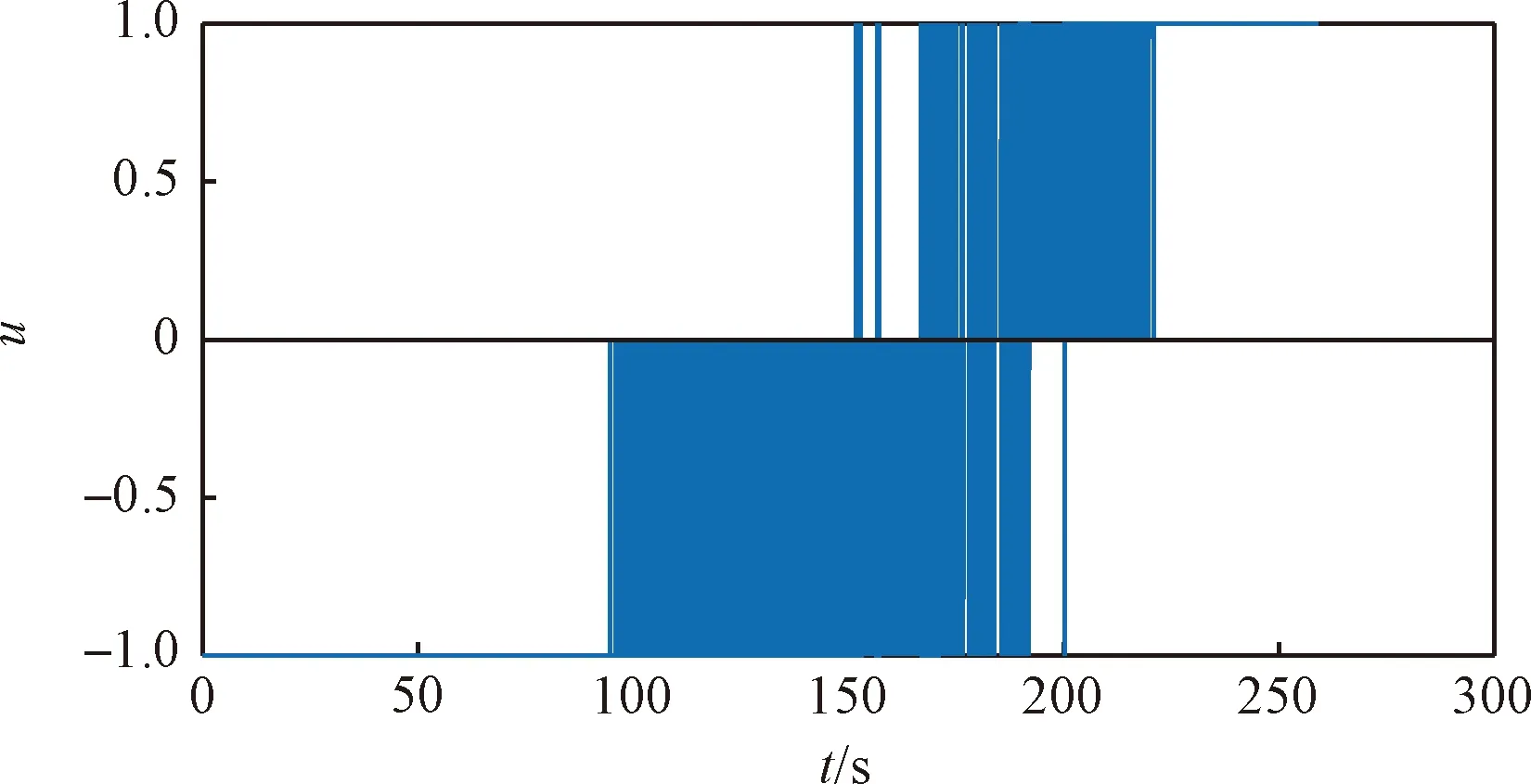
图19 横向运动控制发动机开关曲线Fig.19 Control instruction to lateral motion

为了验证所设计制导算法的性能，采用相同的仿真条件，在纵向平面运动采用文献[11]中的制导方法，横向运动不控的情况下进行仿真，与本文所设计的制导律仿真结果进行对比，终端状态误差对比结果见表3：

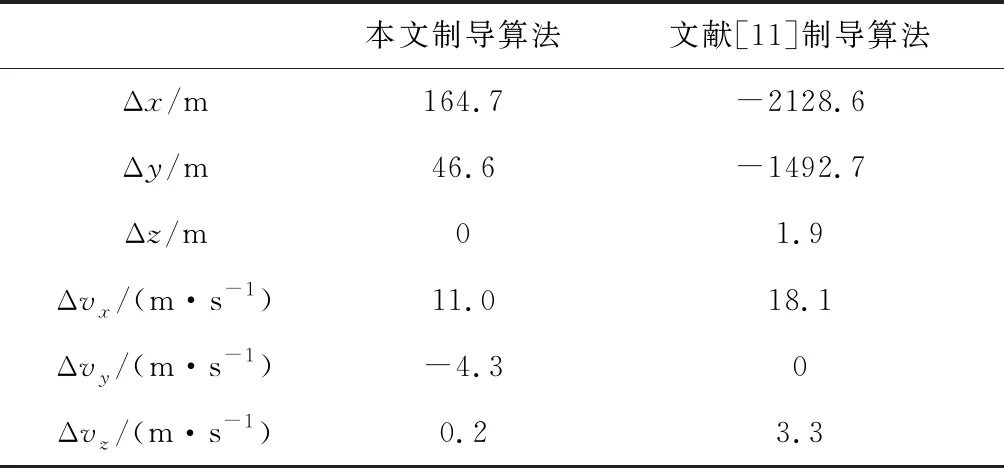
表3 终端状态误差Table 3 Terminal state error

由仿真结果可以看出，软着陆过程中采用本文设计的制导律飞行时，位置变化曲线和速度变化曲线平滑，三个方向上的终端着陆误差能够控制在很小的范围内。同时主减速段结束时，探测器剩余速度大小为11.8 m/s，预定着陆点位于探测器运动方向的前方171.2 m处，能够实现与后续阶段的光滑衔接。另外，主减速段耗时259.04 s，固体发动机燃耗683.60 kg，将此数值作为发射前固发燃料装填质量的参考值。

4.3 制导算法性能

为了进一步验证所设计制导算法的鲁棒性和适应性，根据上面的仿真结果，选取固发燃料装填质量为683.60 kg，仿真过程终止条件设置为燃料耗尽关机，其它仿真条件不变，在目标着陆点纬度36 °N～37.6 °N的覆盖范围内进行蒙特卡罗仿真试验，仿真结果如图20、图21所示。

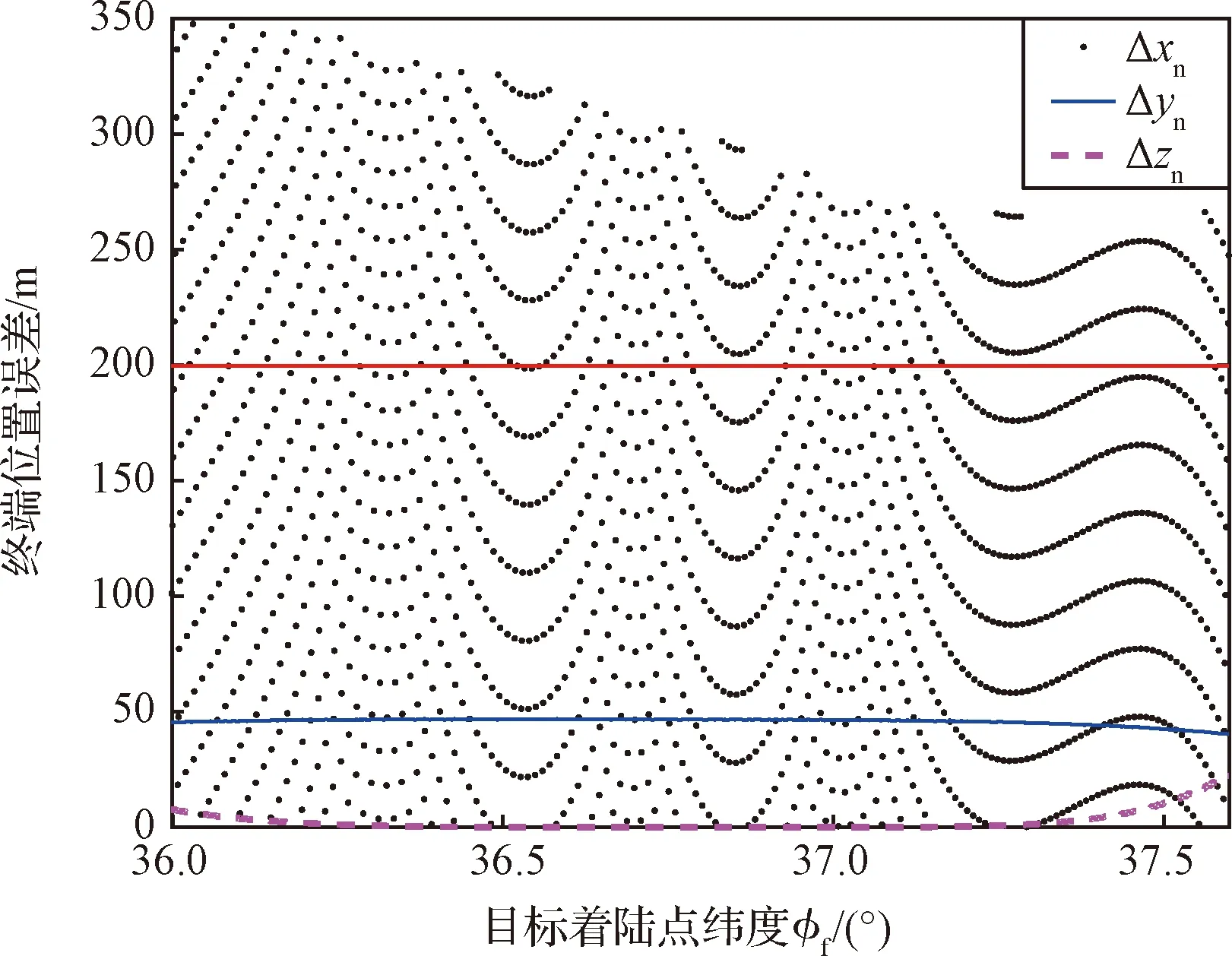
图20 终端位置误差随目标着陆点纬度变化曲线Fig.20 Terminal position error with latitude of target landing site

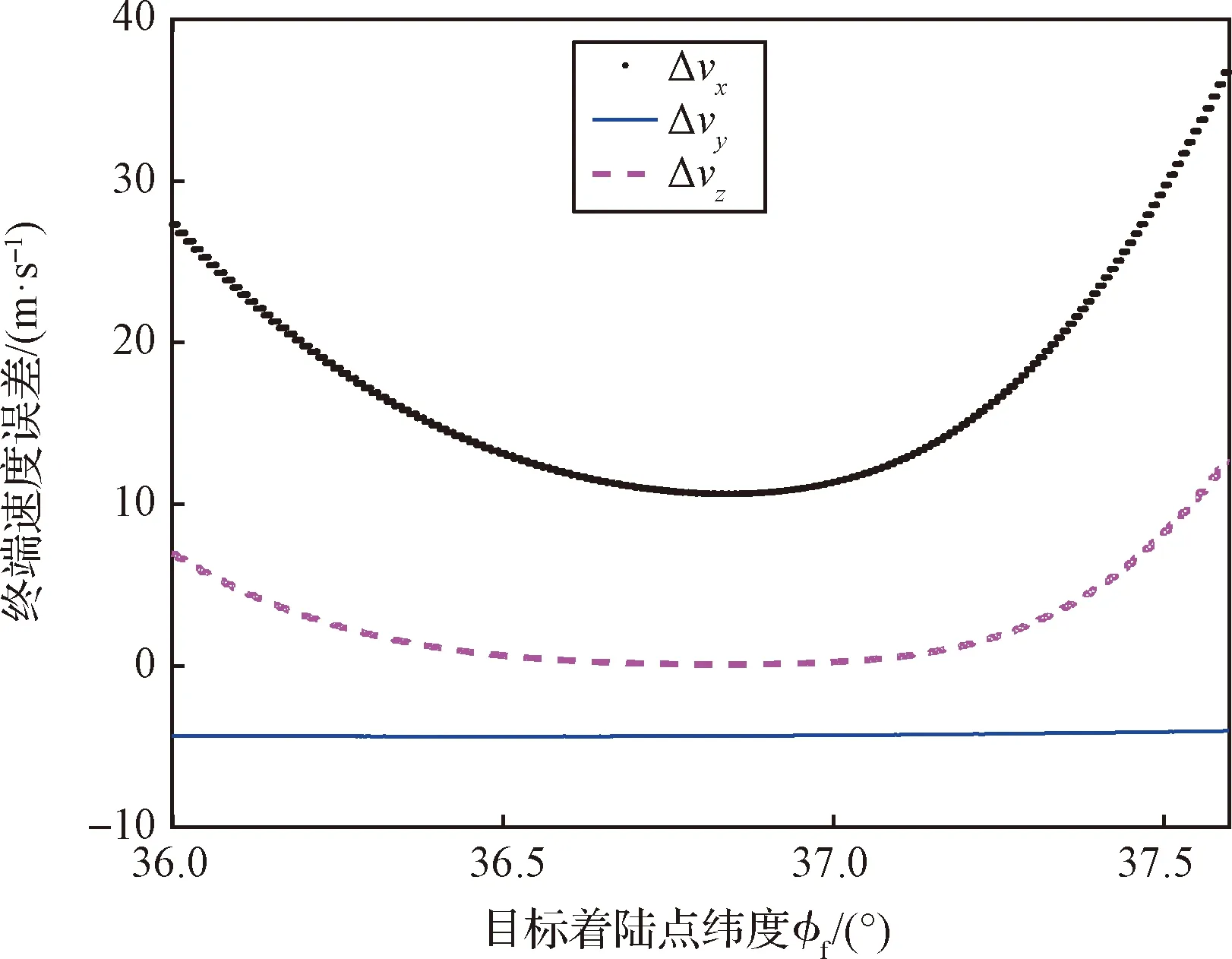
图21 终端速度误差随着陆点纬度变化曲线Fig.21 Terminal velocity error with latitude of target landing site

从仿真结果可以看出，x方向的终端位置误差散布在0～350 m的范围内，且大部分结果满足容许误差200 m的要求；而终端速度误差在目标着陆点纬度逐渐远离原始预定着陆点纬度(36.8173 °N)的过程中，呈现出增大的趋势。z方向的终端位置误差受目标着陆点纬度变化的影响较小，能够保持在很小的范围内；而终端速度误差的变化趋势与x方向相同。对于y方向，由于横向运动单独采用小推力姿控发动机进行控制，因此在横向偏差一定的情况下，y方向的终端位置误差和终端速度误差始终能够控制在允许误差范围内。综上所述，在一定的目标着陆区域内，终端位置误差和终端速度误差能够控制在合理的范围，所设计的制导算法表现出了很好的适应能力。

5 结 论

主发动机采用固体火箭发动机的月球探测器具有显著的经济优势，本文针对这类经济型月球探测器精确定点软着陆主减速段的实时在线制导算法进行了详细的研究，将探测器主减速段的运动分为纵向平面运动和横向运动两部分分别设计制导律。纵向平面运动采用改进显式制导算法和点火角搜索技术，实现了对高程和航程的精确控制；对于横向运动的控制，首先基于ZEM/ZEV最优反馈制导律给出横向制导指令，然后根据发动机特性，采用PWPF将连续形式的制导指令调制为脉冲形式。仿真结果表明：

1)点火角搜索算法能够在很短的时间内优化搜索得到满足终端航向位置约束的点火角修正值，具有很好的实时性和稳定性；

2)飞行过程中运动状态和制导指令变化曲线平滑，三个方向上的终端着陆误差均控制在很小的范围内，同时所设计的改进显式制导算法解决了末段局部时间内姿态角突变的问题；

3)所设计制导算法具有自主性、实时性和一定的鲁棒性，在一定的目标着陆区域内都具有很好的适应能力。