需求不确定下P-Hub公路客运综合枢纽选址研究*

龙思，黄晴，郭权

(长沙理工大学 交通运输工程学院，湖南 长沙 410114)

枢纽选址问题研究以运输网络为背景，运输网络由交错的起始点与目的点连接组成，在这样的系统中，OD间的直接运输既不实际也没有成本效应。针对枢纽选址问题，Sibel A.A.等对其研究方向进行了讨论，包括P-Hub枢纽问题和含固定费用的枢纽选址问题；Puerto J.等在枢纽有容量约束的条件下研究单分配中值问题，通过预处理过程解决变量，并通过增加有效不等式组合来强化模型；Sibel A.A.等考虑不确定性因素进行枢纽选址，不确定性来源于枢纽建设成本和OD间流量需求两方面；熊孝娟等对外界因素造成流量的不确定性进行建模，解决枢纽网络在面对干扰时的调节能力问题；王达等建立基于乘客需求的综合客运枢纽信息重要度模型，提高客运枢纽的服务水平；刘杰等分析交通枢纽客流量的变化特点，建立城市交通枢纽短期客流量组合预测模型；杨年等对容量分配下空铁联运网络设计进行研究，优化枢纽的运营能力；康凯等针对弹性需求下枢纽选址，考虑特定枢纽的随机生效模式，从博弈论角度提出一种能实现平战网络性能权衡的枢纽选址策略。现有研究只考虑OD间的流量需求不确定性，未考虑枢纽换乘系数对需求的影响；将单分配和多分配枢纽选址问题分别考虑，研究不具有针对性，各个角度的研究均不够透彻；未对不确定性与确定性进行比较分析。为此，该文在OD需求不确定的情境下，提出无容量的P-Hub选址问题，流量不确定性以不确性集合形式表现，建立2种不确定规划模型，将不确定转化为相应的分布函数，在相应约束条件下分别使期望成本和α-成本最小，并用算例对模型进行验证。

1 模型建立

1.1 问题描述

枢纽在运输网络中是从起点到终点进行流量收集和分配的设施，在运输网络中起到产生规模经济的作用。P-Hub选址的目的是在运输网络中选P个枢纽，使OD上的流量经过这些枢纽的运输费用最小。该文讨论无容量限制的多分配P-Hub枢纽选址问题的鲁棒性，非枢纽间不能直接链接。

在运输网络中，客流量集中到枢纽，通过枢纽间的集中运输实现规模经济。之前的研究中，各OD间的客流量已知，解决P-Hub枢纽选址问题的关键是处理需求不确定性。而现实生活中需求很大程度上会受到外界因素的影响。因此，在传统P-Hub枢纽问题的基础上考虑需求不确定性因素对运输成本鲁棒性进行分析。

1.2 模型假设

对模型作如下假设：1)运输方式单一；2)运输网络规模较小；3)网络中运输车辆充足；4)不确定系数具有独立性。

1.3 模型构建

为表示事件发生的置信度，引入不确定测度。

定义2(不确定变量)：一个不确定变量是从三元空间到实数集的可测函数，即对于任意实数的Borel集B，集合{ξ∈B}={γ∈Γ|ξ(γ)∈B}为一个事件。

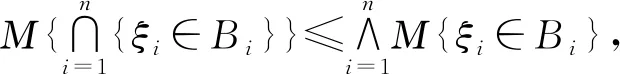
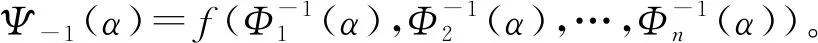
定义5：不确定变量ξ的期望值由式(1)计算。

(1)

引理3：假设ξ1，ξ2，…,ξn分别是具有不确定性分布的自变量，Φ1，Φ2,…,Φn为其对应的分布函数，若f(x1,x2,…,xn)相对于x1,x2,…,xn严格单调递增，则不确定变量的期望值ξ=f(ξ1,ξ2,…,ξn)可由式(2)计算。

(2)

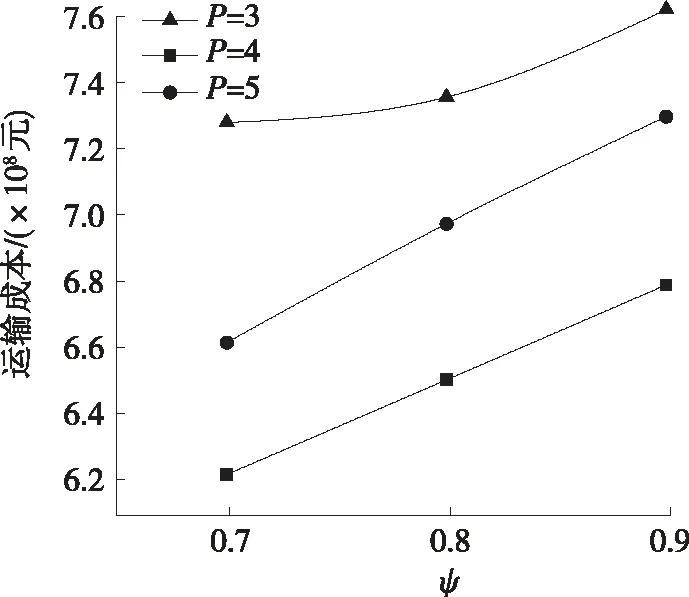
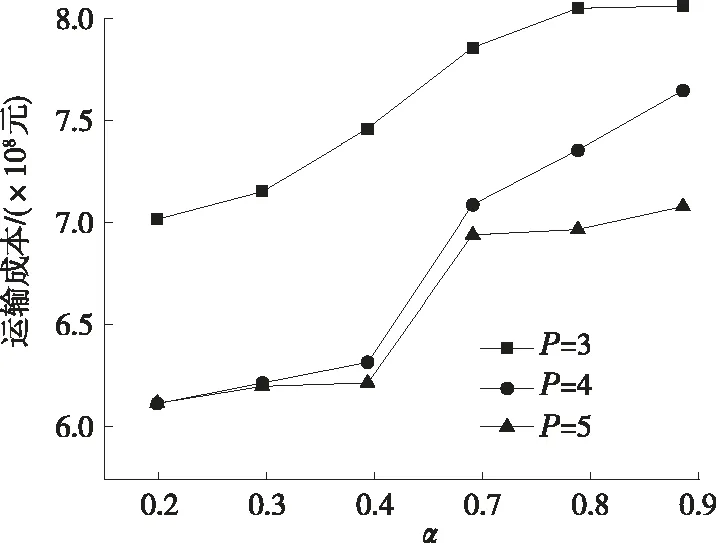
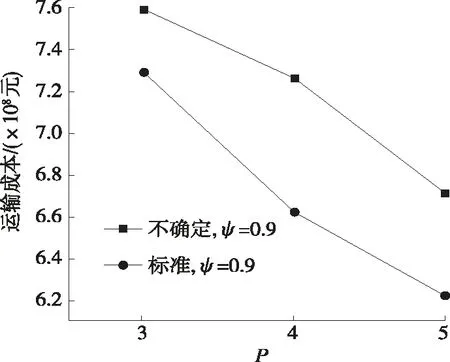
例如：设a

当α=0.9时，Φ-1(0.9)=0.2b+0.8c，E[ξ]=(a+2b+c)/4。

1.4 不确定模型建立

由于P-Hub选址问题与P-median公式类似，也被称为P-Hub中值问题。设有n个节点，每个节点都可以是出发点、目的地或潜在的枢纽选择点。从n个节点中选择P个枢纽，所有枢纽节点彼此连接。每个非枢纽节点完全连接到单个枢纽，2个非枢纽节点之间不直接连接。为便于描述，对参数进行设置，设i为节点，ξi为假定不确定变量的始发地i到目的地j的流量，cik为非枢纽节点i到枢纽节点k的单位运输成本，fk为枢纽位于节点k时的建设固定成本，φ为枢纽间长途移动系数，λ为出发点i运输到枢纽的成本系数，β为枢纽分配到目的地点的成本系数，取λ=β=1，仅考虑枢纽换乘系数的影响。P-Hub枢纽选址问题的决策变量为：

如果xkk的值为1，表示节点k被分配给自己，也就是说节点k实际上是一个枢纽节点。总成本由固定成本、将节点i连接到枢纽节点的成本、将目的地节点连接至枢纽节点的成本、枢纽之间连接成本组成，有：

总成本如下：

为便于分析，令

1.4.1 期望成本最小化模型

不确定变量的度量通常采用期望值，即不确定测度意义下的平均值。根据这一准则，具有不确定流的P-Hub枢纽选址问题的最小期望成本为：

(3)

式中：E为不确定变量的期望算子。

式(3)的约束中，第一个公式表示要求选择精确的P个枢纽点，第二个公式表示确保每个节点被分配给一个且仅分配给一个枢纽，第三个公式表示标准完整性约束。

引理4：假设所有的ξij都是独立的不确定变量，且不确定分布为Φij，可将式(3)转化为等效模型(4)。

(4)

对于任意的i,j对，gij(x)≥0，设S={(i′,j′):gi′j′(x)>0}，则总成本为：

(5)

式(5)在(i′,j′)∈S内是关于ξi′j′的严格递增函数，因为所有的ξij都是独立的，ξi′j′也是独立的，由引理3可得：

gij(x))dα

加上与Φij-1(α)gij(x)相对应的ξijgij(x)，gij(x)=0，可得：

在定理4的条件下，从引理2可得：

由于E[ξij]是所有i和j的一个精确期望值，模型(4)本质上是一个经典的无容量的P-hub枢纽选址模型，不存在不确定性。

1.4.2α-成本期望最小化模型

文献[14]将机会约束规划引入不确定决策系统建模中，文献[15-16]讨论了不确定条件的约束规划的优化。根据这一模型准则，建立在给定置信水平下使成本最小化即α-成本最小化模型(α-CMM)：

(6)

引理5：假设所有的ξij是具有规则不确定性分布的自变量Φij，可将α-CMM模型转化为等效模型(7)。

(7)

根据不确定性分布的定义，有：

(8)

为了简化，将X按照下式进行描述：

i,k=1,2,…,n}

如果ξij为某些特定类型的不确定分布，则有以下推论：

推论1：如果ξij=Ζ(aij,bij,dij)是Z的不确定变量，则模型(7)可写成：

(0.5≤α≤1)

(0<α<0.5)

模型参数如下：Wij表示起点i到目的地点j的总需求量，即经过枢纽的总需求；xijkm表示由i到j经过枢纽k、m的流量。

2 算法设计

采用MATLAB编写粒子群算法对模型进行求解。粒子群算法通过设计一种无质量的粒子来模拟鸟群中的鸟，粒子仅具有速度和位置两个属性，速度代表移动的快慢，位置代表移动的方向。每个粒子在搜索空间中单独搜寻最优解，将其记为当前个体极值，并将个体极值与整个粒子群里的其他粒子共享，找到最优的那个个体极值作为整个粒子群的当前全局最优解。粒子群中的所有粒子根据自己找到的当前个体极值和整个粒子群共享的当前全局最优解来调整自己的速度和位置。

PSO初始化为一群随机粒子(随机解)，然后通过迭代找到最优解。在每次迭代中，粒子通过跟踪2个极值(pbest,gbest)来更新自己。在找到2个最优值后，粒子通过下式更新自己的速度和位置：

vi=vi+c1×rand()×(pbesti-xi)+c2×

rand()×(gbesti-xi)

xi=xi+vi

vi=w×vi+c1×rand()×(pbesti-xi)+

c2×rand()×(gbesti-xi)

式中：i=1,2,…,N;N为群中粒子总数；vi为粒子速度，如果vi大于vi的最大值vmax(大于0)，则vi=vmax；rand()为介于(0,1)之间的随机数；xi为粒子当前位置；c1和c2为学习因子，c1=1.5，c2=2.0；w为惯性因子，其值为非负，w=0.99。

3 算例分析

下面通过算例分析，检验上述模型的有效性。采用《从统计看民航2004》中的数据，考虑20个待选枢纽节点，每个节点的建设固定成本与GPS坐标定位见表1。假设节点之间运输单位成本与节点间距离成比例，设cik=10×dik、cik=cki，即单位成本矩阵是对称的。起点i与终点j之间的流量不确定，表2为待选枢纽节点之间的不确定需求流量，表3为待选节点之间需求流量期望值(由引理3计算得出)，即用期望成本最小化模型计算的期望值。如数据(45,48,50)表示从起点1到终点2的曲折不确定流量，48为最可能的流量，45为最小流量，50为最大流量。当然曲折不确定流量也可以是确定的数值，常数可看成特殊的曲折不确定流量，即服从Z(b,b,b)分布。表4为运用α-成本最小化模型计算得出的节点间需求流量期望值。

表1 部分城市的直角坐标值与枢纽固定成本值

表2 部分城市间的不确定需求流量 人次

表3 部分城市间的需求流量期望值 人次

表4 α=0.8时部分城市间的需求流量期望值 人次

节点之间的实际距离由下式计算：

化简得d=Rarccos[cos(x1-x2)cosy1cosy2+siny1siny2]。其中A、B两点的地理坐标分别为(x1,y1)、(x2,y2)，过A、B两点的大圆的劣弧长即为两点的实际距离。R=6 370 km为地球半径。计算结果见表5、表6。

表5 ECMM模型的计算结果

表6 α-CMM模型的计算结果(ψ=0.8)

由表5、表6可知：对于期望成本最小化模型，枢纽换乘系数ψ增大时，期望成本增大；系数固定不变时，网络总成本值随着枢纽数量的增多而减少；P=4时，网络总成本最小。对于α-成本最小化模型，枢纽数值一定时，成本值随着成本置信水平α的增大而增大。如图1、图2所示，P=4、ψ=0.8与P=4、ψ=0.8、α=0.9所选的枢纽点是一致的，表明不确定模型具有稳定性；P=4时，ψ=0.8与ψ=0.9的结果一致。而根据表6，除α=0.7和α=0.8外，其余置信水平状态下所得枢纽皆为[3,9,11,12]，说明所建立的模型具有鲁棒性。

图1 P=4、ψ=0.8时的结果

图2 P=4、ψ=0.8、α=0.9时的结果

采取的粒子群算法收敛速度快，迭代100次时已收敛(见图3)。图4、图5为两模型的运输成本计算结果，图6为不同枢纽数对应的运输成本结果与标准模型结果的比较。

图3 粒子群算法的收敛速度

图4 期望成本模型枢纽-成本图

图5 α-成本模型枢纽-成本图

图6 需求不确定与需求确定的比较

4 结论

针对需求不确定的P-Hub选址问题，建立期望成本最小化模型与α-成本最小化模型，将不确定的需求流量转换为不确定变量的期望值，并设计粒子群算法对模型进行求解。结论如下：

(1)满足最优解时，需求不确定性不会导致枢纽位置发生较大改变，即使改变，也是邻近枢纽间的移动。

(2)枢纽位置的细微变化可削减需求不确定性对运输成本的影响，并获得成本节约。将运量需求不确定性因素考虑到运输网络中，相对于运量需求确定的情况更具有使用和研究价值。