大跨径悬索桥基准索股线形调整研究

焦明东

(上海同济检测技术有限公司 上海 200009)

引言

悬索桥施工过程中，主缆一旦安装就位，其线形完全由结构体系、自重以及施工荷载和温度变化决定，后期主缆线形无法像斜拉桥一样通过张拉拉索轻易的进行调整，因此施工过程中对于主缆在自重作用下的初始线形应给予充分的重视。对于悬索桥主缆架设，目前多采用预制绳股法(PPWS法)，根据PPWS法施工工序控制要点，基准索股的线形控制则是整个主缆线形控制的基准，其线形调整精度直接决定了后续索股和主缆的架设精度，因此基准索股的线形调整成为悬索桥上部结构施工的重中之重，施工过程中需要反复观测和调整，直至达到设计控制目标。由于塔偏、温度和塔高的变化，基准索股的线形调整过程并非完全处于理想状态，因此根据实际施工状态计算基准索股的架设线形成为确保悬索桥主缆架设精度的关键，也是悬索桥施工监控的重要内容之一[1]。

针对施工中多种因素对悬索桥基准索股线形的影响，相关专家学者展开了大量研究。依托润扬长江大桥基准索股架设，薛光雄等[2]提出采用影响系数的方法进行温度和塔偏影响的修正，并提出了悬索桥基准索股线形的测控方法。基于抛物线理论，郭福等[3]推导了基准索股架设过程中各种影响因素对于索股垂度的影响公式，并通过实际项目得到了相应调整系数。基于弹性悬链线模型，王亮等[4]推导了悬索桥基准索股的悬链线计算方法，并对中跨、边跨主缆调整系数进行了精度验证，结果证明中跨主缆精度较高。基于基准索股的悬链线模型，谭红梅等[5]分别推导了边跨和中跨索长调整的精确解析计算方法，该方法能够考虑主塔偏位、索股温度的影响，但无法考虑主塔相对高差对中跨基准索股线形的影响。

基于悬链线理论，本文推导了适用于地锚式悬索桥边跨和主跨的基准索股悬链线公式，公式涉及塔偏、塔高等影响因素，并根据基准索股线形协调条件推导了索股有应力索长和垂度之间的函数关系，通过与有限元精确计算值对比发现，小里程侧边跨最大误差为-3.676%，中跨最大误差为-0.003%，解析计算结果具有较好的计算精度，能够满足基准索股的线形调整需要；大里程侧边跨最大误差为-20.661%，误差超过10%，可在进行适当的放大调整系数后进行工程应用。本文系统研究了悬链线理论在基准索股线形调整过程中的应用，充分考虑了多种因素的影响，对于未来类似工程可提供可资借鉴的经验。

1 基准索股标准状态计算

在悬索桥基准索股架设过程中不可避免的存在状态误差，其合成效应则主要体现在索股线形上，如果按照标准状态进行索股线形调整则存在造成较大的误差，影响基准索股线形调整的效率和精度。因此充分考虑多种影响因素的作用，对基准索股受力进行适当的简化分析，选择基准索股线形的精确计算公式是基准索股架设线形的重要保证。

1.1 索股受力的基本假设

基准索股的标准状态是指基准温度20.0℃、零塔偏和零塔高偏差时，通过参数识别和测量数据修正设计参数进行计算，并根据基准索股无应力长度不变的原则确定的基准索股线形状态。为了方便基准索股线形计算，计算过程采用如下基本假设：

(1)索股材料线弹性。基准索股材料(高强平行钢丝束)为线弹性材料，正常受力范围内，应力与应变呈线性关系；

(2)索股材料理想柔性。索股在受力计算过程中，只承担拉力作用而不承担受压和抗弯作用；

(3)索股小变形。不考虑主缆横截面在变形前后的变化，基准索股截面面积在自重作用下的变化量十分微小，可忽略截面变化带来的线质量变化。

1.2 索长调整量的测控方式分析

基准索股线形调整采用如下计算思路：将控制点高程、塔偏实测值代入基准索股线形悬链线方程，通过计算得到标准状态和施工状态的垂度偏差，然后根据垂度与索股有应力索长之间的微分关系进行调整。基准索股线形调整确定调整控制点的过程中，通常采用如下两种测控方式：

(1)选择跨中索股上的固定点，结合非线性有限元计算结果对基准索股里程和高程进行调整，直至标志点里程和高程均达到控制目标值；

(2)固定跨中里程位置，结合基准索股悬链线解析计算结果调整基准索股垂度，直至标志位置高程达到控制目标值。

采用测控方式(1)时，索股标志点与跨中点并不一定完全重合，需要同时调整索股里程和高程，调整工作量大且索长调整量存在较大误差；从计算角度而言，测控方式(2)为测控方式(1)的特殊情况。本文基准索股线形调整采用测控方式(2)。

2 基准索股垂度与索长关系计算

2.1 基于悬链线方程的索长计算

在基准索股架设过程中，竖直方向所受荷载为自重，可简化为沿弧长的均匀荷载q，自重作用下基准索股呈悬链线，且满足线性应力-应变关系，基准索股受力如图1所示。

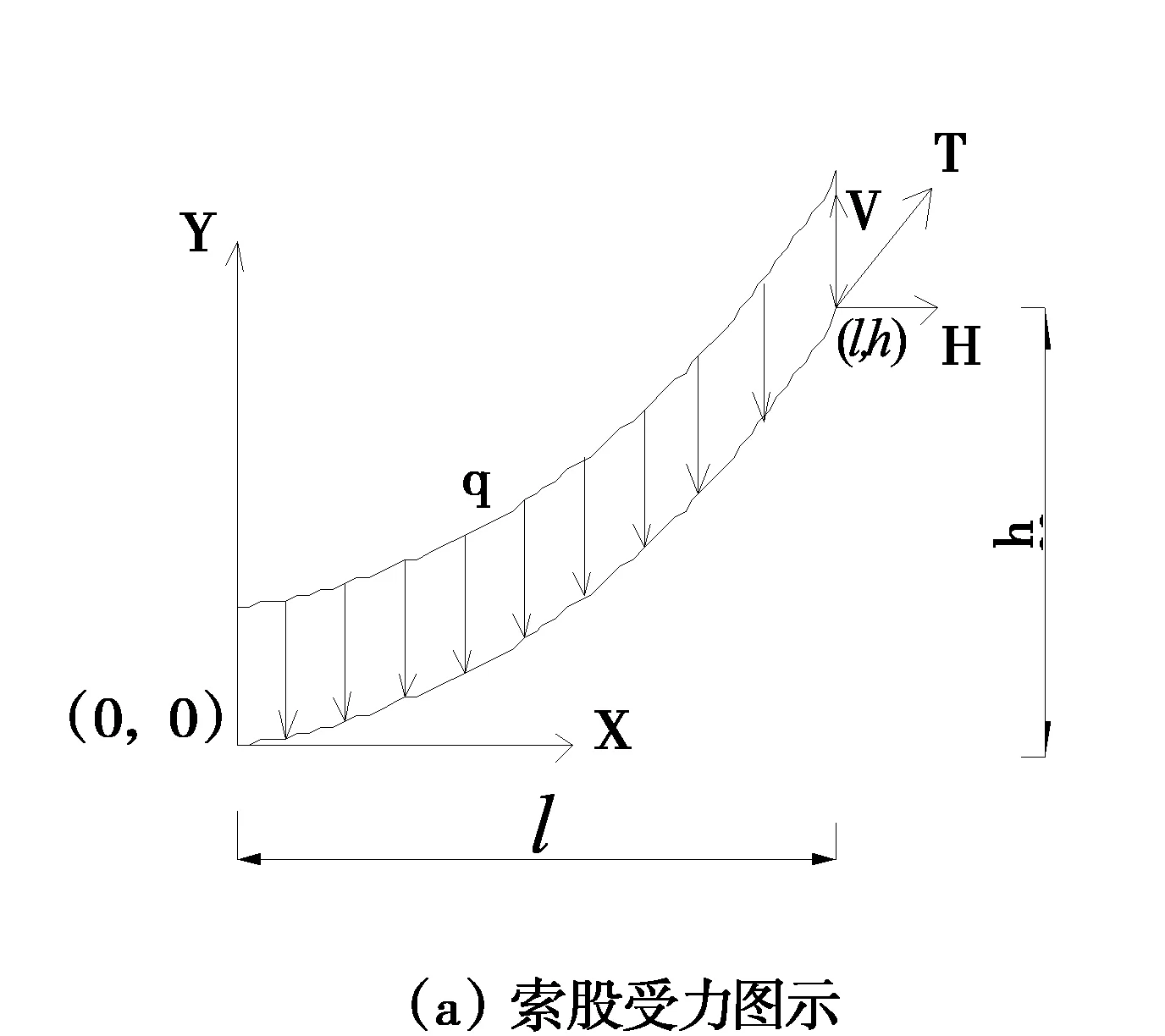
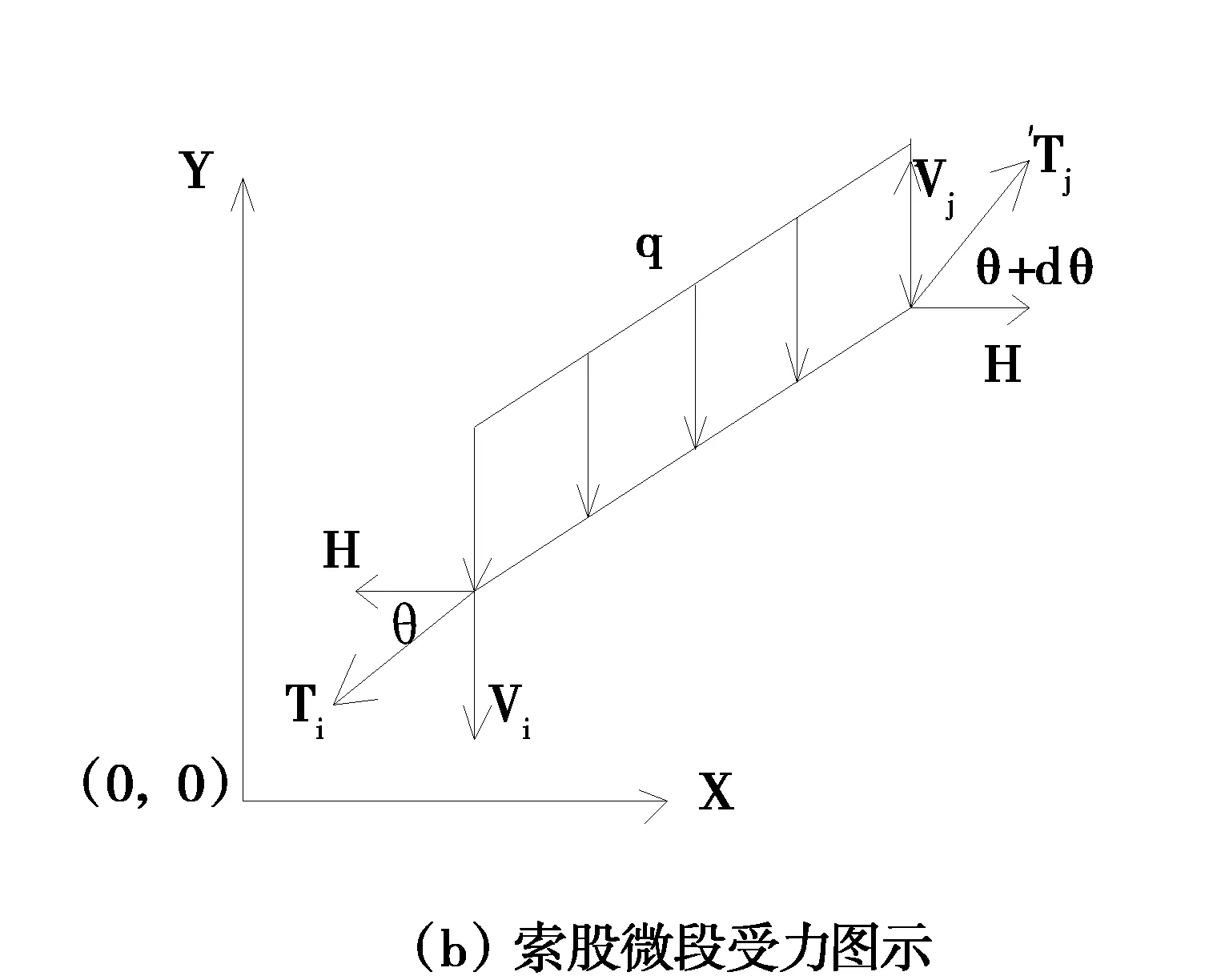
图1 基准索股受力图示

选择基准索股微段进行受力分析见图1(b)，微段受力平衡微分方程如下式所示：

H·tan(θ+dθ)-H·tan(θ)+q·ds=0

(1)

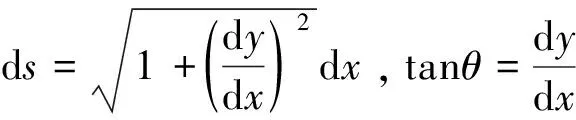
根据三角函数关系，基准索股基本平衡微分方程简化如下式所示：

(2)

式中：H为基准索股水平张拉力；

q为基准索股竖向均布荷载；

y为基准索股竖向位移；

x为基准索股距左侧0点水平向距离。

对上式进行二次积分可以得到下式：

(3)

(4)

则标准温度下的基准索股有应力长度计算公式如下：

(5)

2.2 基准索股垂度与索长微分关系计算

基准索股跨中点的坐标值为(l/2,h/2-f)，代入悬链线方程得到下式：

(6)

综合上述公式可知，基准索股单跨应力索长S及本跨跨中处垂度f均是关于无量纲常数c的函数，分别对c求微分，则索股应力长度与跨中垂度存有如下微分关系：

(7)

3 工程应用

3.1 工程概况

某地锚式悬索桥跨越某水库，全长为1366.0m，跨径布置为：(3×40.0+4×40.0+3×50.0)m(T梁)+(3×50.0+3×50.0)m(钢板组合梁)+700.0m(悬索桥)+2×40.0m(T梁)，主桥为单跨700.0m简支钢箱梁悬索桥，主缆跨径布置为(310.0+700.0+175.0)m，桥梁总体布置见图2。

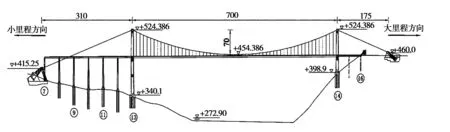
图2 某地锚式悬索桥整体布置图(尺寸单位：m)

主缆采用预制平行钢丝索股，通过PPWS法编织而成。每根主缆由85根索股组成，每根索股由127根φ5.0mm的预制平行钢丝组成，其抗拉承载能力fpk=1770MPa，弹性模量E=2.02×105MPa，线质量m=19.96kg/m。吊索纵向标准间距为12.0m，主塔侧边吊索距主塔中心距离为14.0m。

根据施工过程基准索股线形相关监测数据，基准索股架设工况下索股线形计算主要控制点坐标见表1。

表1 主要控制点坐标(单位：m)

3.2 有限元模型

采用通用有限元软件Midas Civil-2019 建立基准索股架设工况下的悬索桥有限元模型，其中主塔采用梁单元，基准索股采用索单元，边界条件设置与施工过程边界条件一致。根据基准索股的架设进度，本文仅建立左、右侧基准索股和主塔模型，共405个节点、454个单元，基准索股架设阶段有限元模型见图3。

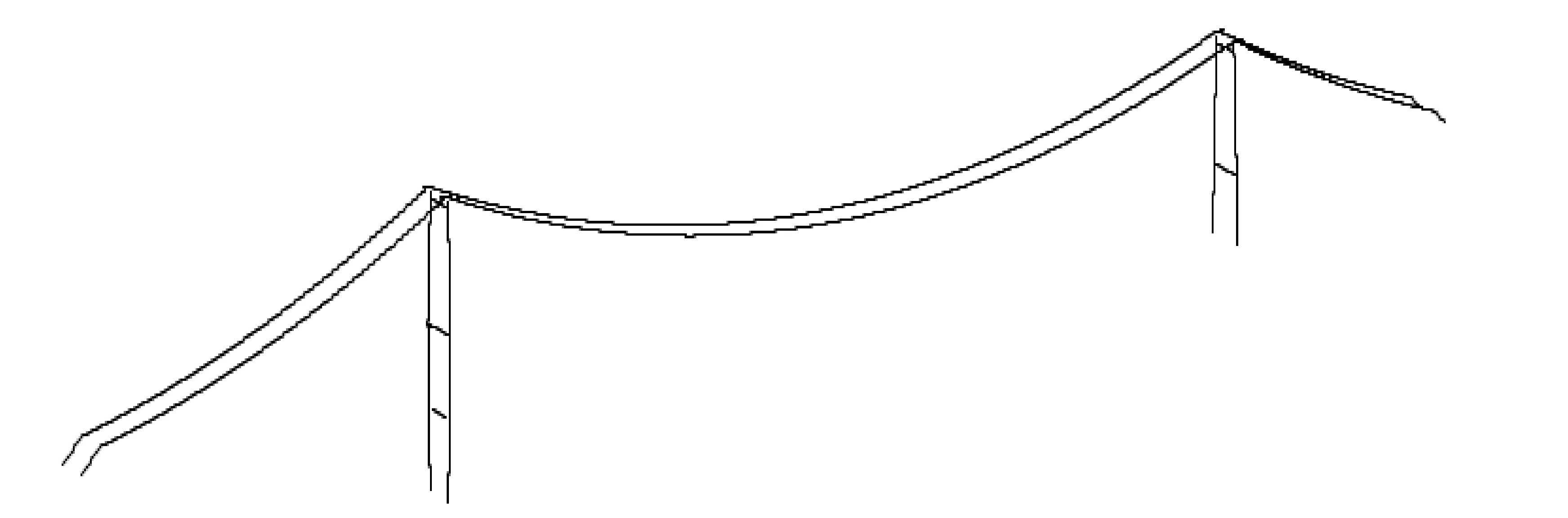
图3 地锚式悬索桥基准索股架设阶段有限元模型图

3.3 结果对比分析

根据地锚式悬索桥设计控制数据以及基准索股架设工况下施工监控过程中识别的控制参数，结合第二节推导基准索股垂度与有应力索长关系公式，与有限元模型计算结果进行对比，结果见表2。

表2 基准索股定位影响因素控制对比分析表

从表2可知，基于悬链线线形方程的基准索股的调缆公式与非线性有限元分析结果对比发现，调缆公式中小里程侧边跨(310.0m)、中跨(700.0m)和大里程侧边跨(主缆跨径为175.0m)的误差分别为-3.676%、-0.003%和-20.661%，这与文献[4-5]结果趋势相同。小里程侧和中跨调缆公式误差均小于5%，能够满足工程精度要求，可直接进行工程应用；大里程侧调缆公式误差超过10%，可在进行适当放大基准索股调整量后进行工程应用。

4 结论

基准索股的线形调整是悬索桥主缆施工线形控制的关键一环，因此应对基准索股的线形精度进行严格控制。鉴于基准索股线形受到塔偏、塔高等因素影响，需要在索股应力索长和垂度计算公式中进行修正。基于基准索股的悬链线公式和边界协调条件，本文推导分析了能够适用于边跨和中跨的应力索长与垂度之间的函数关系，通过与有限元计算结果对比，结果发现除大里程侧精度稍差，需要进行适当的放大索股调整量进行工程应用外，小里程侧和中跨精度较高，能够直接进行基准索股调整应用。